Zagadnienia
6. Metody iteracyjne Kryłowa
W dalszym ciągu przedmiotem naszego zainteresowania będzie układ równań ![]() , którego rozwiązanie oznaczymy (jak zwykle) przez
, którego rozwiązanie oznaczymy (jak zwykle) przez ![]() . O ile nie będzie jasno zaznaczone, że jest inaczej, będziemy przyjmować że początkowe przybliżenie rozwiązania,
. O ile nie będzie jasno zaznaczone, że jest inaczej, będziemy przyjmować że początkowe przybliżenie rozwiązania, ![]() , jest dowolnie zadanym wektorem w
, jest dowolnie zadanym wektorem w ![]() (na przykład,
(na przykład, ![]() ).
).
Tym razem rozważymy pewien wariant metody projekcji, w którym rozmiar podprzestrzeni będzie powiększał się wraz z postępem iteracji. Kolejne przybliżenie ![]() będziemy dobierać w taki sposób, by
będziemy dobierać w taki sposób, by ![]() oraz spełniało pewien dodatkowy warunek, na przykład — minimalizowało pewną miarę błędu na przestrzeni Kryłowa
oraz spełniało pewien dodatkowy warunek, na przykład — minimalizowało pewną miarę błędu na przestrzeni Kryłowa
gdzie ![]() jest residuum początkowym. (Zwróć uwagę, że przestrzeń Kryłowa jest rozpięta przez kolejne wektory metody potęgowej, o której więcej w rozdziale LABEL:sec:xxx — to nie przypadek!). Tam, gdzie nie będzie to prowadziło do nieporozumień, będziemy pomijali parametry przestrzeni Kryłowa i pisali po prostu
jest residuum początkowym. (Zwróć uwagę, że przestrzeń Kryłowa jest rozpięta przez kolejne wektory metody potęgowej, o której więcej w rozdziale LABEL:sec:xxx — to nie przypadek!). Tam, gdzie nie będzie to prowadziło do nieporozumień, będziemy pomijali parametry przestrzeni Kryłowa i pisali po prostu ![]() zamiast
zamiast ![]() .
.
Metody zbudowane zgodnie z powyższym schematem będziemy ogólnie nazywać metodami Kryłowa. Jak za chwilę zobaczymy, taki sposób konstrukcji iteracji pozwoli metodzie samodzielnie ,,dostosować się” do własności macierzy, przez co metody Kryłowa, w przeciwieństwie do metod typu relaksacji, będą w stanie wykorzystać korzystne własności macierzy do przyspieszenia zbieżności: coś, czego ani metody stacjonarne, ani proste metody projekcji nie były w stanie osiągnąć!
Jasne jest, że przestrzenie Kryłowa tworzą wstępujący ciąg podprzestrzeni:
Łatwo pokazać, że nie tylko same przybliżenia ![]() , ale także błędy i residua na
, ale także błędy i residua na ![]() -tym kroku metody Kryłowa można powiązać z pewnymi przestrzeniami Kryłowa:
-tym kroku metody Kryłowa można powiązać z pewnymi przestrzeniami Kryłowa:
Stwierdzenie 6.1
Jeśli ![]() , to
, to ![]() oraz
oraz ![]() .
.
Z tego faktu wynika, że metody przestrzeni Kryłowa są metodami wielomianowymi: zarówno błąd, jak i residuum dadzą wyrazić się jako pewien wielomian macierzy ![]() działający na, odpowiednio, błędzie albo residuum początkowym:
działający na, odpowiednio, błędzie albo residuum początkowym:
Wniosek 6.1
Jeśli ![]() , to błąd
, to błąd ![]() jest postaci
jest postaci ![]() i analogicznie residuum
i analogicznie residuum ![]() jest postaci
jest postaci ![]() , gdzie
, gdzie ![]() są pewnymi rzeczywistymi współczynnikami.
są pewnymi rzeczywistymi współczynnikami.
Ćwiczenie 6.1
Udowodnij powyższe stwierdzenie i wniosek.
Wystarczy zauważyć, że ![]() jest postaci
jest postaci ![]() .
.
Konstrukcja dobrej metody Kryłowa powinna więc (jeśli mielibyśmy zachować ducha metod projekcji z poprzedniego rozdziału) zmierzać w stronę wskazania takiego wielomianu, by norma błędu była jak najmniejsza — na każdym kroku iteracji będziemy wtedy musieli rozwiązać pewne zadanie optymalizacyjne. W zależności od wyboru sposobu miary błędu i warunku optymalności, dostaniemy inną metodę iteracyjną: CG, GMRES, PCR, BiCG i inne. W niniejszym wykładzie omówimy pokrótce tylko najpopularniejsze: CG dla macierzy symetrycznych i dodatnio określonych oraz GMRES dla pozostałych. Należy pamiętać, że w zależności od konkretnego zadania, inne metody mogą okazać się bardziej skuteczne od tutaj omawianych.
W praktycznej implementacji, metody przestrzeni Kryłowa są metodami, w których do ich realizacji musimy jedynie umieć wykonać mnożenie macierzy przez wektor — nie jest potrzebne odwoływanie się do poszczególnych elementów lub części macierzy (co było konieczne w metodach opartych na podziale macierzy, takich jak np. metoda Gaussa–Seidela). Metody, które wymagają wykonywania jedynie mnożenia macierzy przez wektor, a nie odwołują się do poszczególnych elementów macierzy, nazywamy metodami operatorowymi (ang. matrix-free methods). Są one szczególnie pożądane w przypadku, gdy macierz ma nieregularną strukturę i jest bardzo wielkiego rozmiaru, a także w przypadku, gdy sama macierz po prostu nie jest jawnie wyznaczona.
Innym ważnym zastosowaniem metod iteracyjnych Kryłowa jest szybka realizacja jednego kroku tzw. niedokładnej metody Newtona rozwiązywania układu równań nieliniowych, por. rozdział 10.2.4.
Ćwiczenie 6.2
Czy metoda
Jacobiego
Richardsona
najszybszego spadku
jest metodą operatorową?
Na zakończenie wskażemy ciekawą teoretyczną właściwość metod Kryłowa opartych na minimalizacji. Przez ![]() będziemy oznaczali normę energetyczną wektora
będziemy oznaczali normę energetyczną wektora ![]() , indukowaną przez symetryczną, dodatnio określoną macierz
, indukowaną przez symetryczną, dodatnio określoną macierz ![]() ,
,
Twierdzenie 6.1 (metody Kryłowa oparte na minimalizacji błędu albo residuum w normie energetycznej)
Niech ![]() będzie pewną macierzą symetryczną i dodatnio określoną i niech
będzie pewną macierzą symetryczną i dodatnio określoną i niech ![]() -ta iteracja metody Kryłowa,
-ta iteracja metody Kryłowa, ![]() , będzie określona przez jeden z warunków:
, będzie określona przez jeden z warunków:
minimalizacji błędu:
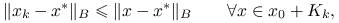
albo
minimalizacji residuum:
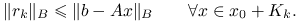
Wtedy metoda jest dobrze określona i znajduje dokładne rozwiązanie ![]() najpóźniej po
najpóźniej po ![]() iteracjach (jest to tzw. własność skończonego stopu).
iteracjach (jest to tzw. własność skończonego stopu).
Powyższe twierdzenie stosuje się do wielu konkretnych metod Kryłowa znajdujących się w powszechnym użyciu. Przykładowo, w metodzie CG (którą dokładniej omówimy w rozdziale 6.1), zdefiniowanej dla macierzy ![]() symetrycznej i dodatnio określonej, iterację będziemy określać warunkiem minimalizacji błędu przy
symetrycznej i dodatnio określonej, iterację będziemy określać warunkiem minimalizacji błędu przy ![]() , natomiast w metodzie GMRES (opisanej w rozdziale 6.2) wybierzemy warunek minimalizacji residuum dla
, natomiast w metodzie GMRES (opisanej w rozdziale 6.2) wybierzemy warunek minimalizacji residuum dla ![]() .
.
Część druga powyższego twierdzenia — o skończonym stopie metody — ma znaczenie głównie teoretyczne. Wynika to z dwóch przesłanek:
gdy
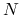 jest bardzo duże, wykonanie
jest bardzo duże, wykonanie 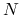 iteracji, nawet jeśli każda kosztuje tylko
iteracji, nawet jeśli każda kosztuje tylko 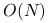 flopów, jest zwykle ponad nasze możliwości obliczeniowe;
flopów, jest zwykle ponad nasze możliwości obliczeniowe;w implementacji metody stosuje się rozmaite chwyty służące maksymalnemu obniżeniu czasochłonności i pamięciożerności algorytmu, które zwykle opierają się na subtelnych zależnościach pomiędzy wyznaczanymi wartościami pośrednimi; gdy algorytm realizujemy w arytmetyce skończonej precyzji, z powodu błędów zaokrągleń tracimy te relacje i z postępem iteracji będą one zwykle coraz gorzej spełnione — co w efekcie doprowadzi także do utraty własności skończonego stopu algorytmu.
Dowód
(twierdzenia 6.1)
Rozważmy najpierw przypadek 6.1, tzn. minimalizacji normy błędu. Pokażemy, że w ogólności ![]() jest dobrze określony przez warunek minimalizacji, gdyż jest zdefiniowany jako rozwiązanie pewnego liniowego zadania najmniejszych kwadratów.
jest dobrze określony przez warunek minimalizacji, gdyż jest zdefiniowany jako rozwiązanie pewnego liniowego zadania najmniejszych kwadratów.
Jeśli przez ![]() oznaczymy macierz, której kolumnami są wektory tworzące bazę
oznaczymy macierz, której kolumnami są wektory tworzące bazę ![]() , to każdy
, to każdy ![]() daje się zapisać w postaci
daje się zapisać w postaci ![]() , gdzie
, gdzie ![]() jest wektorem o tylu współrzędnych, jaki jest wymiar
jest wektorem o tylu współrzędnych, jaki jest wymiar ![]() (oznaczmy go
(oznaczmy go ![]() ). Podstawiając do minimalizowanego wyrażenia, dostajemy zadanie znalezienia
). Podstawiając do minimalizowanego wyrażenia, dostajemy zadanie znalezienia ![]() takiego, że
takiego, że
| (6.1) |
(wtedy ![]() ).
).
Na mocy założenia istnieje macierz ![]() symetryczna i dodatnio określona taka, że
symetryczna i dodatnio określona taka, że ![]() (dlatego nazywamy ją pierwiastkiem z
(dlatego nazywamy ją pierwiastkiem z ![]() ), a stąd wynika, że
), a stąd wynika, że ![]() . Znaczy to, że zadanie minimalizacji (6.1) możemy zapisać w równoważnej postaci
. Znaczy to, że zadanie minimalizacji (6.1) możemy zapisać w równoważnej postaci
| (6.2) |
Jest to standardowe zadanie najmniejszych kwadratów,
gdzie ![]() jest macierzą prostokątną pełnego rzędu, natomiast
jest macierzą prostokątną pełnego rzędu, natomiast ![]() . A zatem
. A zatem ![]() jest wyznaczone jednoznacznie.
jest wyznaczone jednoznacznie.
Na mocy wniosku 6.1, dowolny ![]() spełnia
spełnia ![]() , gdzie
, gdzie ![]() jest pewnym wielomianem stopnia co najwyżej
jest pewnym wielomianem stopnia co najwyżej ![]() takim, że
takim, że ![]() . Jeśli oznaczymy przez
. Jeśli oznaczymy przez ![]() zbiór wielomianów stopnia co najwyżej
zbiór wielomianów stopnia co najwyżej ![]() o wyrazie wolnym równym 1, to warunek minimalizacji błędu możemy sformułować w równoważnej postaci
o wyrazie wolnym równym 1, to warunek minimalizacji błędu możemy sformułować w równoważnej postaci
| (6.3) |
W szczególności, dla wielomianu ![]() — będącego przeskalowanym wielomianem charakterystycznym macierzy
— będącego przeskalowanym wielomianem charakterystycznym macierzy ![]() — mamy, że
— mamy, że ![]() oraz oczywiście
oraz oczywiście ![]() jest stopnia nie większego niż
jest stopnia nie większego niż ![]() , a więc
, a więc ![]() . Z drugiej strony, na mocy twierdzenia Cayley'a–Hamiltona,
. Z drugiej strony, na mocy twierdzenia Cayley'a–Hamiltona, ![]() , skąd
, skąd ![]() . Znaczy to, że przynajmniej dla
. Znaczy to, że przynajmniej dla ![]() zadanie minimalizacji ma (jednoznaczne) rozwiązanie, którym jest
zadanie minimalizacji ma (jednoznaczne) rozwiązanie, którym jest ![]() — a więc, że metoda ma własność skończonego stopu.
— a więc, że metoda ma własność skończonego stopu.
Dowód drugiej części twierdzenia, dotyczącej przypadku, gdy ![]() jest zadany warunkiem minimalizacji residuum, zostawiamy jako ćwiczenie.
jest zadany warunkiem minimalizacji residuum, zostawiamy jako ćwiczenie.
Ćwiczenie 6.3
Uzupełnij powyższy dowód.
- Sposób I
Dla dowodu drugiego przypadku zauważmy, że
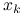 znów jest dobrze określony jako rozwiązanie pewnego liniowego zadania najmniejszych kwadratów postaci
znów jest dobrze określony jako rozwiązanie pewnego liniowego zadania najmniejszych kwadratów postaci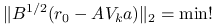
oraz na mocy wniosku 6.1 zachodzi
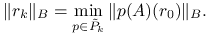
(6.4) Dalszy ciąg dowodu jest identyczny jak poprzednio.
- Sposób II
Oznaczmy chwilowo macierz indukującą normę energetyczną, w której minimalizujemy residuum, symbolem
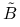 . Wystarczy skorzystać z pierwszej części twierdzenia, biorąc
. Wystarczy skorzystać z pierwszej części twierdzenia, biorąc 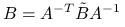 , gdyż
, gdyż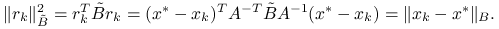
Wniosek 6.3
Jeśli po ![]() -tej iteracji metody Kryłowa o własności skończonego stopu następuje stagnacja:
-tej iteracji metody Kryłowa o własności skończonego stopu następuje stagnacja: ![]() , to znaczy, że właśnie znaleziono rozwiązanie dokładne,
, to znaczy, że właśnie znaleziono rozwiązanie dokładne, ![]() .
.
Dowód
Jeśli ![]() , to oczywiście
, to oczywiście ![]() . Ponieważ jednak musi być
. Ponieważ jednak musi być ![]() (skończony stop po
(skończony stop po ![]() iteracjach!) to oznacza, że
iteracjach!) to oznacza, że ![]() .
.
6.1. Metoda gradientów sprzężonych (CG)
Algorytm CG został uznany za jeden z 20 najważniejszych algorytmów numerycznych opracowanych w XX wieku.
W niniejszym rodziale będziemy zakładać, że kwadratowa macierz rzeczywista ![]() rozmiaru
rozmiaru ![]() jest symetryczna,
jest symetryczna, ![]() , oraz jest dodatnio określona,
, oraz jest dodatnio określona,
Przy tym założeniu, można określić normę energetyczną indukowaną przez ![]() , zadaną tożsamością
, zadaną tożsamością
Metodę gradientów sprzężonych, w skrócie CG (ang. conjugate gradients), zdefiniujemy początkowo w sposób niejawny. Kolejne przybliżenie ![]() określimy jako wektor z podprzestrzeni afinicznej
określimy jako wektor z podprzestrzeni afinicznej ![]() , minimalizujący w tej podprzestrzeni błąd w normie energetycznej indukowanej przez
, minimalizujący w tej podprzestrzeni błąd w normie energetycznej indukowanej przez ![]() :
:
| (6.5) |
Naturalnie, taka definicja może budzić w nas nieco wątpliwości, co do jego obliczalności (w sformułowaniu warunku minimalizacji występuje szukane przez nas rozwiązanie dokładne, ![]() ).
).
Stwierdzenie 6.2 (CG jako metoda bezpośrednia)
Zadanie minimalizacji (6.5) ma jednoznaczne rozwiązanie. Jeśli ![]() jest macierzą, której kolumny tworzą bazę
jest macierzą, której kolumny tworzą bazę ![]() , to
, to ![]() jest dane wzorem
jest dane wzorem ![]() , gdzie
, gdzie ![]() spełnia układ równań
spełnia układ równań
| (6.6) |
Ponadto, w arytmetyce dokładnej, metoda CG znajduje dokładne rozwiązanie w co najwyżej ![]() iteracjach.
iteracjach.
Dowód
Jest to natychmiastowy wniosek z twierdzenia 6.1, dla przypadku minimalizacji błędu gdy ![]() . Zależność (6.6) to nic innego jak układ równań normalnych dla zadania najmniejszych kwadratów (6.2).
. Zależność (6.6) to nic innego jak układ równań normalnych dla zadania najmniejszych kwadratów (6.2).
Z powyższego lematu wynika (por. (6.6)), że ![]() jest istotnie obliczalny: do jego wyznaczenia nie jest nam efektywnie potrzebna znajomość rozwiązania!
jest istotnie obliczalny: do jego wyznaczenia nie jest nam efektywnie potrzebna znajomość rozwiązania!
6.1.1. Implementacja
Aby wyznaczyć ![]() , nie będziemy bezpośrednio rozwiązywać układu (6.6) — byłoby to, wraz z postępem iteracji, coraz bardziej kosztowne, ze względu na zwiększający się rozmiar zadania najmniejszych kwadratów. Spróbujemy znaleźć tańszy sposób wyznaczania
, nie będziemy bezpośrednio rozwiązywać układu (6.6) — byłoby to, wraz z postępem iteracji, coraz bardziej kosztowne, ze względu na zwiększający się rozmiar zadania najmniejszych kwadratów. Spróbujemy znaleźć tańszy sposób wyznaczania ![]() .
.
Ponieważ ![]() jest symetryczna, istnieje baza ortogonalna w
jest symetryczna, istnieje baza ortogonalna w ![]() złożona z wektorów własnych
złożona z wektorów własnych ![]() :
:
Oznaczając przez ![]() macierz, której kolejne kolumny są wektorami własnymi
macierz, której kolejne kolumny są wektorami własnymi ![]() ,
,
mamy, że ![]() jest macierzą ortogonalną,
jest macierzą ortogonalną, ![]() , a ponadto
, a ponadto ![]() ma rozkład:
ma rozkład:
gdzie
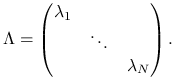 |
Gdyby baza przestrzeni ![]() była
była ![]() –ortogonalna (z powodów historycznych, jej elementy oznaczymy
–ortogonalna (z powodów historycznych, jej elementy oznaczymy ![]() tak, że
tak, że ![]() ), tzn.
), tzn. ![]() dla
dla ![]() , to wtedy macierz równań normalnych byłaby diagonalna,
, to wtedy macierz równań normalnych byłaby diagonalna,
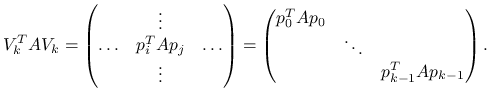 |
Wtedy kolejną iterację można wyznaczyć z jawnego wzoru:
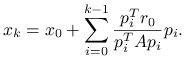 |
(6.7) |
Zatem potrzebna jest nam skuteczna metoda wyznaczania bazy ortogonalnej w przestrzeni ![]() …. Oczywiście, ze względu na koszt obliczeniowy i pamięciowy, generowanie i następnie ortogonalizacja oryginalnego zestawu wektorów
…. Oczywiście, ze względu na koszt obliczeniowy i pamięciowy, generowanie i następnie ortogonalizacja oryginalnego zestawu wektorów ![]() rozpinających
rozpinających ![]() nie ma większego sensu. W zamian, wykorzystamy specjalne własności wektorów otrzymywanych w trakcie działania metody.
nie ma większego sensu. W zamian, wykorzystamy specjalne własności wektorów otrzymywanych w trakcie działania metody.
Lemat 6.1 (o ortogonalności residuów)
Residuum na ![]() -tym kroku,
-tym kroku, ![]() , jest prostopadłe do
, jest prostopadłe do ![]() . Ponadto
. Ponadto ![]() .
.
Dowód
Uzasadnienie pierwszej części łatwo wynika z układu równań normalnych (6.6), określającego pośrednio ![]() . Rzeczywiście, ponieważ
. Rzeczywiście, ponieważ ![]() , to z (6.6) wynika, że
, to z (6.6) wynika, że ![]() . Upraszczając wyrazy z
. Upraszczając wyrazy z ![]() , dostajemy
, dostajemy ![]() , czyli
, czyli ![]() .
.
Druga część wynika natychmiast z faktu, że ![]() , skąd
, skąd ![]() i w konsekwencji, odejmując stronami od
i w konsekwencji, odejmując stronami od ![]() , dochodzimy do
, dochodzimy do ![]() . Tymczasem z definicji przestrzeni Kryłowa
. Tymczasem z definicji przestrzeni Kryłowa ![]() .
.
Z powyższego wynika, że jeśli ![]() , to
, to ![]() , a więc dopóki nie trafimy w rozwiązanie dokładne,
, a więc dopóki nie trafimy w rozwiązanie dokładne, ![]() , kolejne przestrzenie Kryłowa w metodzie
, kolejne przestrzenie Kryłowa w metodzie ![]() tworzą ściśle wstępujący ciąg przestrzeni,
tworzą ściśle wstępujący ciąg przestrzeni, ![]() .
.
W dalszm ciągu założymy więc, że ![]() — a więc, że
— a więc, że ![]() . Przypuśćmy, że mamy już zadaną bazę
. Przypuśćmy, że mamy już zadaną bazę ![]() –ortogonalną
–ortogonalną ![]() przestrzeni
przestrzeni ![]() i znamy
i znamy ![]() ,
, ![]() . Naszym celem będzie wyznaczenie
. Naszym celem będzie wyznaczenie ![]() ,
, ![]() oraz
oraz ![]() . Z zależności (6.7) mamy, że
. Z zależności (6.7) mamy, że
| (6.8) |
gdzie
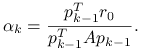 |
(6.9) |
Obkładając (6.8) macierzą ![]() i odejmując obustronnie od
i odejmując obustronnie od ![]() dostajemy dodatkowo zależność rekurencyjną na residua,
dostajemy dodatkowo zależność rekurencyjną na residua,
| (6.10) |
Potrzeba nam jeszcze zależności rekurencyjnej pozwalającej wyznaczyć ![]() — ostatni wektor bazy ortogonalnej dla
— ostatni wektor bazy ortogonalnej dla ![]() (wcześniejsze znamy z założenia indukcyjnego). Ponieważ z lematu 6.1 wynika, że
(wcześniejsze znamy z założenia indukcyjnego). Ponieważ z lematu 6.1 wynika, że ![]() , znaczy to, że
, znaczy to, że
Mnożąc skalarnie tę równość przez ![]() dostajemy z założenia
dostajemy z założenia ![]() -ortogonalności
-ortogonalności
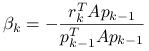 |
(6.11) |
i podobnie, że ![]() oraz wszystkie następne współczynniki są równe zero (ponieważ z lematu o residuach
oraz wszystkie następne współczynniki są równe zero (ponieważ z lematu o residuach ![]() jest ortogonalne do
jest ortogonalne do ![]() , a
, a ![]() dla
dla ![]() ).
Zatem ostatecznie dostajemy kolejną elegancką zależność rekurencyjną, tym razem na wektory bazy
).
Zatem ostatecznie dostajemy kolejną elegancką zależność rekurencyjną, tym razem na wektory bazy ![]() –ortogonalnej dla
–ortogonalnej dla ![]() :
:
| (6.12) |
Ponieważ ![]() , tym samym zależności (6.8)—(6.11) stanowią domknięty układ: startując z zadanego
, tym samym zależności (6.8)—(6.11) stanowią domknięty układ: startując z zadanego ![]() , jesteśmy w stanie wyznaczać kolejne przybliżenia.
, jesteśmy w stanie wyznaczać kolejne przybliżenia.
Okazuje się, że powyższe wzory można jeszcze bardziej wymasować, otrzymując w końcu bardzo zwarty i tani algorytm:
Metoda CG
| while not stop |
| begin |
| |
| |
| |
| |
| |
| |
| |
| |
| end |
Jak widać, całą iterację da się wykonać, przechowując w pamięci tylko kilka wektorów (a nie, jak możnaby się obawiać, całą przestrzeń ![]() ), a najdroższym jej elementem jest mnożenie macierzy przez wektor.
), a najdroższym jej elementem jest mnożenie macierzy przez wektor.
Najpierw wykażemy, że
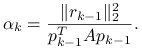 |
(6.13) |
Ponieważ z założenia ![]() dla każdego
dla każdego ![]() , to (mnożąc obustronnie tę równość przez
, to (mnożąc obustronnie tę równość przez ![]() i odejmując stronami od
i odejmując stronami od ![]() ) zachodzi także
) zachodzi także ![]() . Mnożąc skalarnie tę równość przez
. Mnożąc skalarnie tę równość przez ![]() i uwzględniając
i uwzględniając ![]() –ortogonalność kierunków
–ortogonalność kierunków ![]() dochodzimy do wniosku, że
dochodzimy do wniosku, że
Z drugiej zaś strony, mnożąc (6.12) skalarnie przez ![]() otrzymujemy
otrzymujemy
ponieważ ![]() jest prostopadłe do
jest prostopadłe do ![]() , w której zawarty jest wektor
, w której zawarty jest wektor ![]() . Ostatecznie więc
. Ostatecznie więc ![]() dla każdego
dla każdego ![]() . Biorąc
. Biorąc ![]() , z (6.9) otrzymujemy (6.13).
, z (6.9) otrzymujemy (6.13).
Teraz wyprowadzimy prostszą reprezentację współczynnika ![]() .
Z rekurencyjnej zależności pomiędzy residuami (6.10) wynika, że
.
Z rekurencyjnej zależności pomiędzy residuami (6.10) wynika, że
Ponieważ z lematu o ortogonalności residuów ![]() oraz
oraz ![]() jest ortogonalne do
jest ortogonalne do ![]() , to
, to ![]() , więc podstawiając do powyższego wzoru uzyskane przed chwilą nowe wyrażenie na
, więc podstawiając do powyższego wzoru uzyskane przed chwilą nowe wyrażenie na ![]() dostajemy
dostajemy
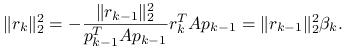 |
Stąd i z (6.13) już wynika wzór na współczynnik ![]() ,
,
Dla dużych ![]() , traktowanie CG jako metody bezpośredniej nie miałoby większego sensu — nie dość, że wykonanie aż
, traktowanie CG jako metody bezpośredniej nie miałoby większego sensu — nie dość, że wykonanie aż ![]() iteracji mogłoby być zadaniem ponad możliwości naszego komputera, to jeszcze dodatkowo algorytm wykorzystuje bardzo specyficzne relacje pomiędzy wektorami, a całość jest przecież w praktyce realizowana w arytmetyce zmiennoprzecinkowej o ograniczonej precyzji, w której te relacje nie zachodzą (w sposób dokładny). Prowadzi to do tego, że w miarę postępu iteracji na przykład wektory
iteracji mogłoby być zadaniem ponad możliwości naszego komputera, to jeszcze dodatkowo algorytm wykorzystuje bardzo specyficzne relacje pomiędzy wektorami, a całość jest przecież w praktyce realizowana w arytmetyce zmiennoprzecinkowej o ograniczonej precyzji, w której te relacje nie zachodzą (w sposób dokładny). Prowadzi to do tego, że w miarę postępu iteracji na przykład wektory ![]() są coraz mniej ortogonalne i tym samym metoda nie musi dotrzeć do dokładnego rozwiązania.
są coraz mniej ortogonalne i tym samym metoda nie musi dotrzeć do dokładnego rozwiązania.
Dlatego w praktyce znacznie bardziej właściwe wydaje się potraktowanie metody CG (i innych metod Kryłowa) jako ,,czystej” metody iteracyjnej i oszacowanie szybkości redukcji błędu podobnie, jak czyniliśmy to w przypadku metod stacjonarnych.
Twierdzenie 6.2 (o zbieżności CG jako metody iteracyjnej)
Po ![]() iteracjach metody CG,
iteracjach metody CG,
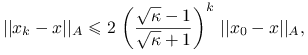 |
gdzie ![]() .
.
Dowód
Skorzystamy z własności (6.3). Zauważmy, że
oraz
zatem wystarczy oszacować wartości wybranego wielomianu ![]() (nasza norma błędu jest i tak nie większa).
Niech
(nasza norma błędu jest i tak nie większa).
Niech ![]() i
i ![]() . Jako
. Jako ![]() w (6.3) weźmy przeskalowany
w (6.3) weźmy przeskalowany ![]() -ty wielomian Czebyszewa,
-ty wielomian Czebyszewa,
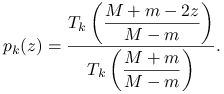 |
Rzeczywiście, ![]() . Ponadto, ponieważ wielomiany Czebyszewa spełniają zależność
. Ponadto, ponieważ wielomiany Czebyszewa spełniają zależność
to
![\max _{{z\in[m,M]}}|p_{k}(z)|\leq\dfrac{1}{T_{k}\left(\dfrac{M+m}{M-m}\right)}=\dfrac{1}{T_{k}\left(\dfrac{\kappa+1}{\kappa-1}\right)}.](wyklady/mo2/mi/mi1299.png) |
Należy więc oszacować ![]() . Ponieważ
. Ponieważ ![]() , to skorzystamy ze wzoru
, to skorzystamy ze wzoru
W szczególności więc, biorąc ![]() mamy
mamy
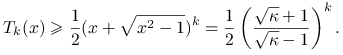 |
Stwierdzenie 6.3
Jeśli macierz ![]() ma
ma ![]() różnych wartości własnych, to metoda CG w arytmetyce dokładnej znajdzie rozwiązanie dokładne
różnych wartości własnych, to metoda CG w arytmetyce dokładnej znajdzie rozwiązanie dokładne ![]() w co najwyżej
w co najwyżej ![]() iteracjach.
iteracjach.
Ćwiczenie 6.5
Udowodnij powyższe stwierdzenie.
Rozważ odpowiednio przeskalowany wielomian ![]() .
.
Przykład 6.1
Kontynuujemy przykład 5.13. Chcąc porównywać cztery metody: Jacobiego, SOR, metodę najszybszego spadku oraz sprzężonych gradientów, będziemy korzystać z macierzy
gdzie ![]() oraz
oraz ![]() jest losową macierzą rozrzedzoną. Zwiększanie parametru
jest losową macierzą rozrzedzoną. Zwiększanie parametru ![]() nie tylko poprawia diagonalną dominację, ale także poprawia uwarunkowanie
nie tylko poprawia diagonalną dominację, ale także poprawia uwarunkowanie ![]() . Jako parametr relaksacji dla SOR wybraliśmy (strzelając w ciemno)
. Jako parametr relaksacji dla SOR wybraliśmy (strzelając w ciemno) ![]() .
.
Zwróćmy uwagę na wyraźną przewagę metody CG nad pozostałymi. Sprawdź, czy podobnie jest dla większych wartości ![]() .
.
Ćwiczenie 6.6
Sprawdź w przykładzie 6.1, czy faktycznie uwarunkowanie macierzy ![]() wpływa na szybkość zbieżności metody CG i najszybszego spadku. Aby zbadać uwarunkowanie macierzy, możesz skorzystać z polecenia
wpływa na szybkość zbieżności metody CG i najszybszego spadku. Aby zbadać uwarunkowanie macierzy, możesz skorzystać z polecenia cond(A), albo wykorzystać estymator uwarunkowania dostępny w pcg.
Ćwiczenie 6.7
Sprawdź, modyfikując kod przykładu 6.1, czy jeśli ![]() nie będzie symetryczna (lub nie będzie dodatnio określona), wpłynie to istotnie na szybkość zbieżności metody CG i najszybszego spadku. Wypróbuj m.in.
nie będzie symetryczna (lub nie będzie dodatnio określona), wpłynie to istotnie na szybkość zbieżności metody CG i najszybszego spadku. Wypróbuj m.in. ![]() dla
dla ![]() (brak symetrii) tak dobranego, by
(brak symetrii) tak dobranego, by ![]() oraz
oraz ![]() dla
dla ![]() takiego, żeby
takiego, żeby ![]() miało i dodatnie, i ujemne wartości własne.
miało i dodatnie, i ujemne wartości własne.
Przykład 6.2
Chcąc porównywać cztery metody: Jacobiego, SOR, metodę najszybszego spadku oraz sprzężonych gradientów dla macierzy jednowymiarowego laplasjanu ![]() . Jako parametr relaksacji dla SOR wybraliśmy wartość optymalną, zgodnie z przykładem 5.11.
. Jako parametr relaksacji dla SOR wybraliśmy wartość optymalną, zgodnie z przykładem 5.11.
Zwróćmy uwagę na wyraźną przewagę metody CG nad pozostałymi metodami iteracyjnymi. Jednak i tak nie wytrzymuje ona konkurencji z metodą bezpośrednią. Ta sytuacja dramatycznie zmieni się, gdy będziemy rozważali dyskretyzacje dwu- lub trójwymiarowego operatora Laplace'a. O ile wtedy metoda CG wciąż ma kłopoty z szybką zbieżnością, to metoda bezpośrednia (typu rozkładu LU) staje się całkowicie bezużyteczna.
6.2. Metoda GMRES
Metoda GMRES (ang. Generalized Minimum RESidual) nie wymaga ani symetrii, ani dodatniej określoności macierzy, jest więc bardziej uniwersalna, choć też w realizacji bardziej kosztowna od CG. Jej szczegółowe omówienie, w tym — wyprowadzenie subtelniejszych oszacowań szybkości zbieżności — wykracza niestety poza ramy niniejszego wykładu (zainteresowani mogą skonsultować m.in. podręcznik [13]).
W tej metodzie, przybliżenie na ![]() -tej iteracji ma minimalizować, w przestrzeni afinicznej
-tej iteracji ma minimalizować, w przestrzeni afinicznej ![]() , residuum (stąd nazwa) mierzone w normie euklidesowej:
, residuum (stąd nazwa) mierzone w normie euklidesowej:
| (6.14) |
Stwierdzenie 6.4 (GMRES jako metoda bezpośrednia)
Zadanie minimalizacji (6.14) ma jednoznaczne rozwiązanie. Jeśli ![]() jest macierzą, której kolumny tworzą bazę
jest macierzą, której kolumny tworzą bazę ![]() , to
, to ![]() jest dane wzorem
jest dane wzorem ![]() , gdzie
, gdzie ![]() jest rozwiązaniem zadania najmniejszych kwadratów względem
jest rozwiązaniem zadania najmniejszych kwadratów względem ![]() ,
,
| (6.15) |
Ponadto, w arytmetyce dokładnej, metoda GMRES znajduje rozwiązanie ![]() w co najwyżej
w co najwyżej ![]() iteracjach.
iteracjach.
Dowód
Jest to bezpośredni wniosek z twierdzenia 6.1, dla przypadku minimalizacji residuum gdy ![]() .
.
Twierdzenie 6.3 (o zbieżności metody GMRES jako metody iteracyjnej)
Jeśli macierz ![]() jest diagonalizowalna (to znaczy
jest diagonalizowalna (to znaczy ![]() i
i ![]() jest macierzą diagonalną5Oczywiście, na diagonali
jest macierzą diagonalną5Oczywiście, na diagonali ![]() znajdują się wartości własne macierzy
znajdują się wartości własne macierzy ![]() . W ogólności więc, zarówno
. W ogólności więc, zarówno ![]() , jak i
, jak i ![]() mogą być zespolone.), to
mogą być zespolone.), to ![]() -ta iteracja GMRES spełnia
-ta iteracja GMRES spełnia
Powyższe twierdzenie jest mało praktyczne, ze względu na to, że zazwyczaj nie znamy macierzy ![]() . Ale jeśli na przykład macierz
. Ale jeśli na przykład macierz ![]() jest normalna, to znaczy
jest normalna, to znaczy ![]() , to wtedy
, to wtedy ![]() i w konsekwencji
i w konsekwencji ![]() .
.
Ćwiczenie 6.8
Niech ![]() będzie macierzą diagonalizowalną. Wykaż, że jeśli
będzie macierzą diagonalizowalną. Wykaż, że jeśli ![]() ma
ma ![]() różnych wartości własnych, to GMRES w arytmetyce dokładnej osiągnie rozwiązanie w co najwyżej
różnych wartości własnych, to GMRES w arytmetyce dokładnej osiągnie rozwiązanie w co najwyżej ![]() krokach.
krokach.
Wynika z poprzedniego twierdzenia, wystarczy wziąć ![]() .
.
6.2.1. Implementacja
Dla ostatecznej skuteczności metody iteracyjnej ważna jest także jej efektywna implementacja. Załóżmy więc, że z powodzeniem wykonaliśmy ![]() kroków metody GMRES i teraz chcemy wyznaczyć
kroków metody GMRES i teraz chcemy wyznaczyć ![]() . Oznaczamy, jak zwykle, przez
. Oznaczamy, jak zwykle, przez ![]() macierz, której kolumny tworzą bazę
macierz, której kolumny tworzą bazę ![]() . Wtedy, jeśli nie osiągnięto jeszcze rozwiązania, to
. Wtedy, jeśli nie osiągnięto jeszcze rozwiązania, to ![]() , zatem
, zatem ![]() . Aby wyznaczyć współczynniki
. Aby wyznaczyć współczynniki ![]() reprezentacji
reprezentacji ![]() w bazie
w bazie ![]() ,
, ![]() , musimy rozwiązać względem
, musimy rozwiązać względem ![]() liniowe zadanie najmniejszych kwadratów,
liniowe zadanie najmniejszych kwadratów,
| (6.16) |
Wydawać by się mogło, że sprawa jest tu prosta, bo ![]() możemy w miarę łatwo wyznaczyć, a potem należałoby skorzystać z jednej z metod rozwiązywania standardowego zadania najmniejszych kwadratów. Jednak jeśli uwzględnić drobny fakt, że do wyznaczenia
możemy w miarę łatwo wyznaczyć, a potem należałoby skorzystać z jednej z metod rozwiązywania standardowego zadania najmniejszych kwadratów. Jednak jeśli uwzględnić drobny fakt, że do wyznaczenia ![]() potrzebna nam będzie znajomość nie samego
potrzebna nam będzie znajomość nie samego ![]() , ale także
, ale także ![]() , sytuacja robi się nieco niezręczna. Dlatego po raz kolejny spróbujemy spreparować bazę
, sytuacja robi się nieco niezręczna. Dlatego po raz kolejny spróbujemy spreparować bazę ![]() i jednocześnie wykorzystać fakt, że
i jednocześnie wykorzystać fakt, że ![]() rozpina podprzestrzeń w
rozpina podprzestrzeń w ![]() (rozpiętej przez
(rozpiętej przez ![]() .
.
Zwróćmy uwagę na to, że jeśli ![]() są bazą ortogonalną w
są bazą ortogonalną w ![]() dla
dla ![]() , to aby rozszerzyć ją do
, to aby rozszerzyć ją do ![]() wystarczy zortogonalizować — zamiast
wystarczy zortogonalizować — zamiast ![]() — wektor
— wektor ![]() . Stosując zmodyfikowany algorytm ortogonalizacji Grama-Schmidta do
. Stosując zmodyfikowany algorytm ortogonalizacji Grama-Schmidta do ![]() :
:
Metoda Arnoldiego wyznaczania bazy ortogonalnej
| for |
| |
| |
| |
| |
| end |
| (6.17) |
gdzie ![]() jest macierzą Hessenberga rozmiaru
jest macierzą Hessenberga rozmiaru ![]() :
:
Opisana tu zmodyfikowana metoda Grama–Schmidta ortogonalizacji bazy przestrzeni Kryłowa nosi nazwę metody Arnoldiego.
Jest to istotny postęp na drodze ku efektywnemu rozwiązaniu zadania minimalizacji (6.16), gdyż podstawiając doń (6.17) mamy, że
— w ostatniej równości skorzystaliśmy z ortogonalności ![]() . Ale przecież
. Ale przecież ![]() (gdzie
(gdzie ![]() ), zaterm
), zaterm ![]() ! Tak więc, zadanie najmniejszych kwadratów (6.16) dla macierzy rozmiaru
! Tak więc, zadanie najmniejszych kwadratów (6.16) dla macierzy rozmiaru ![]() sprowadziliśmy do zadania najmniejszych kwadratów:
sprowadziliśmy do zadania najmniejszych kwadratów:
| (6.18) |
dla macierzy Hessenberga ![]() , rozmiaru
, rozmiaru ![]() (a więc: prawie–trójkątnej!)6Macierz Hessenberga można — przy pomocy (ortogonalnych) przekształceń Givensa — doprowadzić liniowym kosztem do postaci górnej trójkątnej, zob. [9, rozdział 3.5]..
(a więc: prawie–trójkątnej!)6Macierz Hessenberga można — przy pomocy (ortogonalnych) przekształceń Givensa — doprowadzić liniowym kosztem do postaci górnej trójkątnej, zob. [9, rozdział 3.5]..
Stąd dostajemy bazową wersję implementacji algorytmu GMRES:
Metoda GMRES, wersja bazowa
| while not stop |
| {wykonaj ortogonalizację metodą Arnoldiego} |
| |
| |
| |
| |
| {rozszerz bazę |
| |
| |
| {znajdź minimum zadania najmniejszych kwadratów} |
| |
| {zwiększ licznik iteracji} |
| |
| end |
| {rozwiąż ostatnie zadanie najmniejszych kwadratów} |
Zwróćmy uwagę na pewien drobiazg obniżający koszt iteracji: dopóki nie wyznaczymy rozwiązania z żądaną dokładnością (co możemy określić jedynie poprzez analizę residuum, ![]() ), nie musimy znajdować ani
), nie musimy znajdować ani ![]() , ani
, ani ![]() . Dzięki temu, koszt jednej iteracji GMRES jest tylko rzędu
. Dzięki temu, koszt jednej iteracji GMRES jest tylko rzędu ![]() flopów (gdybyśmy wyznaczali
flopów (gdybyśmy wyznaczali ![]() na każdej iteracji, dodawałoby to dodatkowe
na każdej iteracji, dodawałoby to dodatkowe ![]() flopów).
flopów).
Powyższy algorytm w praktyce jest poddawany pewnym drobnym modyfikacjom, związanym z tym, że choć zmodyfikowany algorytm Grama–Schmidta ma numeryczne własności wyraźnie lepsze od klasycznego, to wciąż w realizacji w arytmetyce skończonej precyzji będzie tracił ortogonalność kolumn ![]() . Dlatego uzupełnia się go o warunkową reortogonalizację
. Dlatego uzupełnia się go o warunkową reortogonalizację ![]() : szczegóły opisane są w [9] (tam także są przykłady ukazujące wagę tego dodatkowego kroku) oraz w [13].
: szczegóły opisane są w [9] (tam także są przykłady ukazujące wagę tego dodatkowego kroku) oraz w [13].
Ćwiczenie 6.9
Przeanalizuj zbieżność metody GMRES dla macierzy kwadratowej
gdzie ![]() , a
, a ![]() jest macierzą
jest macierzą ![]() .
.
6.2.2. Wersja z restartem: GMRES(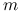 )
)
Pewną wadą metody GMRES jest konieczność zapamiętania na ![]() -tym kroku wszystkich wektorów bazy ortogonalnej przestrzeni Kryłowa
-tym kroku wszystkich wektorów bazy ortogonalnej przestrzeni Kryłowa ![]() . Znaczy to, że nakład obliczeń i, co gorsza, ilość pamięci potrzebnej na wykonanie jednego kroku metody rosną wraz z liczbą iteracji. Aby zniwelować tę przypadłość, zwykle stosuje się restarty metody GMRES co
. Znaczy to, że nakład obliczeń i, co gorsza, ilość pamięci potrzebnej na wykonanie jednego kroku metody rosną wraz z liczbą iteracji. Aby zniwelować tę przypadłość, zwykle stosuje się restarty metody GMRES co ![]() (rzędu kilkunastu–kilkudziesięcu) iteracji: po
(rzędu kilkunastu–kilkudziesięcu) iteracji: po ![]() iteracjach przerywane są obliczenia, a wyznaczone w ten sposób rozwiązanie przybliżone jest używane jako początkowe przybliżenie do kolejnego wywołania metody. W ten sposób co prawda spowalnia się nieco szybkość zbieżności samej metody, ale za to utrzymujemy w ryzach jej zasobożerność: to często jest rozsądny kompromis.
iteracjach przerywane są obliczenia, a wyznaczone w ten sposób rozwiązanie przybliżone jest używane jako początkowe przybliżenie do kolejnego wywołania metody. W ten sposób co prawda spowalnia się nieco szybkość zbieżności samej metody, ale za to utrzymujemy w ryzach jej zasobożerność: to często jest rozsądny kompromis.




