Zagadnienia
10. Wariacje na temat metody Newtona
Podstawowy element metody Newtona — rozwiązywanie równania zlinearyzowanego — w przypadku, gdy ![]() jest duże, może stanowić wąskie gardło całego procesu iteracyjnego. Dlatego w tym i następnym rozdziale poszukamy skutecznych metod ominięcia tego ograniczenia; jednak na początek przytoczymy inną wersję twierdzenia o zbieżności, która (przy silniejszych założeniach) zagwarantuje nam także istnienie rozwiązań.
jest duże, może stanowić wąskie gardło całego procesu iteracyjnego. Dlatego w tym i następnym rozdziale poszukamy skutecznych metod ominięcia tego ograniczenia; jednak na początek przytoczymy inną wersję twierdzenia o zbieżności, która (przy silniejszych założeniach) zagwarantuje nam także istnienie rozwiązań.
10.1. Twierdzenie o istnieniu rozwiązań
W dotychczasowej analizie zakładaliśmy, że rozwiązanie ![]() równania
równania ![]() istnieje. Okazuje się, że nieco modyfikując założenia standardowe można udowodnić i istnienie rozwiązania, i lokalną zbieżność metody Newtona do tego rozwiązania.
istnieje. Okazuje się, że nieco modyfikując założenia standardowe można udowodnić i istnienie rozwiązania, i lokalną zbieżność metody Newtona do tego rozwiązania.
Twierdzenie 10.1 (Kantorowicza, o istnieniu i zbieżności)
Niech ![]() , przy czym
, przy czym ![]() jest niepusty, otwarty i wypukły, i niech
jest niepusty, otwarty i wypukły, i niech ![]() będzie różniczkowalna w
będzie różniczkowalna w ![]() oraz istnieje
oraz istnieje ![]() takie, że
takie, że
Niech istnieje ![]() takie, że
takie, że ![]() jest nieosobliwa oraz dla pewnych dodatnich
jest nieosobliwa oraz dla pewnych dodatnich ![]() zachodzi
zachodzi
przy czym ![]() . Określmy
. Określmy ![]() i załóżmy, że
i załóżmy, że ![]() .
.
Wówczas ciąg ![]() zdefiniowany metodą Newtona jest dobrze określony, co więcej
zdefiniowany metodą Newtona jest dobrze określony, co więcej ![]() oraz ma granicę
oraz ma granicę ![]() , która jest jedynym miejscem zerowym
, która jest jedynym miejscem zerowym ![]() w
w ![]() . Ponadto
. Ponadto
dla ![]() .
.
Dowód
Dowód tego twierdzenia można znaleźć np. w [12, rozdział 12.6.1].
∎10.2. Obniżanie kosztu iteracji
Z punktu widzenia praktycznej realizacji, każdy krok metody Newtona ma parę potencjalnie kosztownych momentów, które teraz przedyskutujemy.
Wyznaczenie wzoru na
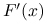 może być trudne: na przykład, gdy
może być trudne: na przykład, gdy 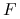 jest zadana bardzo skomplikowaną procedurą (a nie jednolinijkowym wzorem), wtedy ani ręczne, ani automatyczne różniczkowanie
jest zadana bardzo skomplikowaną procedurą (a nie jednolinijkowym wzorem), wtedy ani ręczne, ani automatyczne różniczkowanie 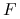 może nie prowadzić do poprawnych czy zadowalających rezultatów. Może też być bardzo żmudne.
może nie prowadzić do poprawnych czy zadowalających rezultatów. Może też być bardzo żmudne.Wyznaczenie wartości
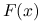 , a zwłaszcza:
, a zwłaszcza: 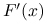 , może być kosztowne. Rzeczywiście,
, może być kosztowne. Rzeczywiście, 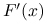 to
to 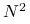 elementów macierzy pochodnej, a dodatkowo — poza najprostszymi przypadkami — pochodna jest zwykle dana bardziej skomplikowanym wyrażeniem niż sama funkcja. Rozsądne jest więc przyjęcie13O ile
elementów macierzy pochodnej, a dodatkowo — poza najprostszymi przypadkami — pochodna jest zwykle dana bardziej skomplikowanym wyrażeniem niż sama funkcja. Rozsądne jest więc przyjęcie13O ile 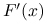 nie jest macierzą rozrzedzoną., że w praktyce koszt wyznaczenia
nie jest macierzą rozrzedzoną., że w praktyce koszt wyznaczenia 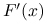 będzie rzędu
będzie rzędu 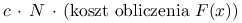 , z raczej dużą stałą
, z raczej dużą stałą 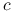 . Nawet wyznaczenie pojedynczej wartości
. Nawet wyznaczenie pojedynczej wartości 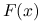 może być w niektórych zadaniach bardzo kosztowne. W [3] wspomina się o
może być w niektórych zadaniach bardzo kosztowne. W [3] wspomina się o 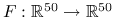 , której jedna wartość kosztowała 100 godzin pracy ówczesnego szybkiego komputera.
, której jedna wartość kosztowała 100 godzin pracy ówczesnego szybkiego komputera.Rozwiązanie układu z
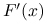 jest potencjalnie najbardziej kosztownym fragmentem iteracji. Rzeczywiście, gdy
jest potencjalnie najbardziej kosztownym fragmentem iteracji. Rzeczywiście, gdy 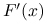 jest macierzą gęstą bez żadnych szczególnych własności, to koszt rozwiązania układu
jest macierzą gęstą bez żadnych szczególnych własności, to koszt rozwiązania układu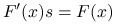
jest rzędu
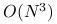 .
.
Te obserwacje prowadzą do kilku heurystycznych sposobów modyfikacji metody Newtona tak, by obniżyć koszt jednej jej iteracji. Czasem — choć nie zawsze, i dlatego te sposoby są ważne! — obniżenie kosztu iteracji będzie skutkowało pogorszeniem szybkości zbieżności metody, ale nawet i wówczas może okazać się, że ostatecznie metoda wolniej zbieżna, ale tańsza, będzie bardziej efektywna od metody Newtona.
10.2.1. Uproszczona metoda Newtona
W uproszczonej metodzie Newtona, najdroższy fragment iteracji Newtona — wyznaczenie rozkładu trójkątnego macierzy pochodnej — usuwamy poza pętlę:
Rzeczywiście, jeśli bowiem na samym początku iteracji dokonamy kosztem ![]() flopów rozkładu LU (lub QR) macierzy
flopów rozkładu LU (lub QR) macierzy ![]() i zapamiętamy czynniki rozkładu, to potem każdy z układów równań:
i zapamiętamy czynniki rozkładu, to potem każdy z układów równań:
będziemy mogli rozwiązać już tylko kosztem nie wyższym niż ![]() ! Oznacza to, że koszt jednej iteracji spada nam do
! Oznacza to, że koszt jednej iteracji spada nam do ![]() , jest więc
, jest więc ![]() -krotnie mniejszy niż w przypadku oryginalnej metody Newtona. Ceną za przyspieszenie jest wyraźne zmniejszenie szybkości zbieżności metody:
-krotnie mniejszy niż w przypadku oryginalnej metody Newtona. Ceną za przyspieszenie jest wyraźne zmniejszenie szybkości zbieżności metody:
Twierdzenie 10.2 (o zbieżności uproszczonej metody Newtona)
Przy standardowych założeniach, istnieją stałe dodatnie ![]() i
i ![]() takie, że jeśli
takie, że jeśli ![]() , to uproszczona metoda Newtona jest zbieżna przynajmniej liniowo do
, to uproszczona metoda Newtona jest zbieżna przynajmniej liniowo do ![]() oraz
oraz
| (10.1) |
Dowód
Zostanie podany później, gdy będziemy dysponowali wygodnym narzędziem do badania tego typu metod.
∎Ćwiczenie 10.1
Zaimplementuj uproszczoną metodę Newtona.
Wystarczy zmodyfikować algorytm realizujący metodę Newtona:
Uproszczona metoda Newtona
| function simplerNewton(x, F, stop) |
| oblicz macierz pochodnej |
| wyznacz rozkład |
| while not stop do begin |
| rozwiąż układ z macierzą trójkątną, |
| x = x - s; |
| end |
| return(x); |
Ćwiczenie 10.2
Metoda Szamańskiego to metoda, w której po ![]() krokach uproszczonej metody Newtona dokonujemy wyznaczenia i rozkładu macierzy pochodnej (czyli restartujemy metodę uproszczoną, biorąc za przybliżenie początkowe ostatnio wyznaczone przybliżenie rozwiązania). Jest to więc coś pośredniego pomiędzy prawdziwą metodą Newtona (w której w każdej iteracji wyznacza się i rozkłada macierz pochodnej) a uproszczoną metodą Newtona (gdzie macierz pochodnej wyznacza się tylko jeden raz).
krokach uproszczonej metody Newtona dokonujemy wyznaczenia i rozkładu macierzy pochodnej (czyli restartujemy metodę uproszczoną, biorąc za przybliżenie początkowe ostatnio wyznaczone przybliżenie rozwiązania). Jest to więc coś pośredniego pomiędzy prawdziwą metodą Newtona (w której w każdej iteracji wyznacza się i rozkłada macierz pochodnej) a uproszczoną metodą Newtona (gdzie macierz pochodnej wyznacza się tylko jeden raz).
Formalnie możemy więc przyjąć, że ![]() kroków uproszczonej metody Newtona to jest ,,jeden duży krok” i określić iterację Szamańskiego następująco:
kroków uproszczonej metody Newtona to jest ,,jeden duży krok” i określić iterację Szamańskiego następująco:
Znajdź wykładnik ![]() taki, że
taki, że
Z definicji metody, ![]() wyznaczamy jako
wyznaczamy jako ![]() -tą iterację uproszczonej metody Newtona startującej z
-tą iterację uproszczonej metody Newtona startującej z ![]() . Na mocy oszacowania błędu uproszczonej metody Newtona mamy więc
. Na mocy oszacowania błędu uproszczonej metody Newtona mamy więc
skąd
A więc metoda ma wykładnik ![]() .
.
Ćwiczenie 10.3
Porównaj efektywność metody Szamańskiego i Newtona w zależności od rozmiaru zadania ![]() , przy następujących modelowych założeniach:
, przy następujących modelowych założeniach:
koszt wyznaczenia
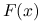 jest równy
jest równy 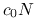
koszt wyznaczenia
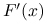 jest równy
jest równy 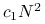
koszt wyznaczenia rozkładu
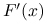 jest równy
jest równy 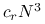
koszt wyznaczenia rozwiązania układu z macierzą
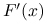 o danym rozkładzie jest równy
o danym rozkładzie jest równy 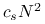
Oczywiście musimy założyć ![]() , w przeciwnym razie obie metody są tożsame.
Dla metody Newtona mamy
, w przeciwnym razie obie metody są tożsame.
Dla metody Newtona mamy
a dla metody Szamańskiego
Stąd ![]() wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy ![]() . Dalej przekształcając, dostajemy warunek wiążący ze sobą
. Dalej przekształcając, dostajemy warunek wiążący ze sobą ![]() i
i ![]() :
:
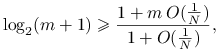 |
co zachodzi dla ![]() dostatecznie dużych względem
dostatecznie dużych względem ![]() .
.
Ćwiczenie 10.4 (liniowa niezmienniczość iteracji Newtona)
Rozważmy równanie ![]() i jego liniową transformację
i jego liniową transformację
gdzie ![]() są nieosobliwymi macierzami rozmiaru
są nieosobliwymi macierzami rozmiaru ![]() . Wykaż, że jeśli tylko
. Wykaż, że jeśli tylko ![]() , to iteracja Newtona dla
, to iteracja Newtona dla ![]() ,
,
jest równoważna metodzie Newtona dla ![]() w tym sensie, że zawsze zachodzi
w tym sensie, że zawsze zachodzi ![]() .
.
Iteracja Newtona dla ![]() to
to
Mnożąc lewostronnie przez ![]() i podstawiając gdzie trzeba
i podstawiając gdzie trzeba ![]() mamy
mamy
Na zakończenie wystarczy zauważyć, że ![]() .
.
Ćwiczenie 10.5
Wykaż, że jeśli spełnione są założenia standardowe oraz metoda Newtona jest zbieżna, to dla dostatecznie dużych ![]() zachodzi
zachodzi
Może to więc być dość prosty test (niezmienniczy ze względu na liniowe transformacje zmiennej niezależnej i zależnej!), pozwalający przypuszczać, że nie zachodzi zbieżność: na przykład, gdy na pewnym kroku metody stwierdzimy ![]() , możemy wtedy uznać prawdopodobny brak zbieżności i zakończyć iterację.
, możemy wtedy uznać prawdopodobny brak zbieżności i zakończyć iterację.
10.2.2. Wpływ niedokładności wyznaczenia pochodnej lub funkcji na zbieżność metody Newtona
Twierdzenie 10.3 (o lokalnej stabilności metody Newtona)
Przy standardowych założeniach, istnieją stałe dodatnie ![]() ,
, ![]() oraz
oraz ![]() takie, że jeśli
takie, że jeśli ![]() oraz
oraz ![]() , to
, to
| (10.2) |
jest dobrze określony oraz
| (10.3) |
gdzie ![]() .
.
Dowód
Dowód znajdziemy np. w [9].
∎Z twierdzenia o lokalnej stabilności metody Newtona można wywnioskować wiele twierdzeń o zbieżności tych modyfikacji metody Newtona, które sprowadzają się do zaburzenia oryginalnej metody Newtona, na przykład twierdzenia o zbieżności uproszczonej metody Newtona.
Dowód
(Twierdzenia 10.2, o zbieżności uproszczonej metody Newtona.) Jeden krok uproszczonej metody Newtona
możemy zapisać w języku twierdzenia o lokalnej stabilności metody Newtona, gdzie
Niech więc ![]() będzie dostatecznie małe tak, by dla
będzie dostatecznie małe tak, by dla ![]() zachodziło twierdzenie o lokalnej stabilności metody Newtona w kuli
zachodziło twierdzenie o lokalnej stabilności metody Newtona w kuli ![]() . Dodatkowo załóżmy, że
. Dodatkowo załóżmy, że ![]() . Wtedy
. Wtedy
i na mocy właśnie tw. o lokalnej stabilności,
Ponieważ z założenia ![]() , to z powyższego wynika, że
, to z powyższego wynika, że
jeśli więc ![]() jest na tyle małe, by dodatkowo
jest na tyle małe, by dodatkowo ![]() , to ciąg
, to ciąg ![]() zawiera się w
zawiera się w ![]() oraz
oraz ![]() musi być zbieżny do zera przynajmniej liniowo.
musi być zbieżny do zera przynajmniej liniowo.
10.2.3. Metoda z przybliżoną pochodną
Jak już wspominaliśmy, innym kłopotliwym momentem w realizacji metody Newtona jest wyznaczanie macierzy pochodnej. Opracowanie dokładnej formuły obliczania ![]() może być żmudne, podatne na ludzkie pomyłki. Uzyskany wzór może być ciężki w implementacji i kosztowny w użyciu.
może być żmudne, podatne na ludzkie pomyłki. Uzyskany wzór może być ciężki w implementacji i kosztowny w użyciu.
Ale, ponieważ metoda Newtona jest jedynie metodą przybliżoną, można zaryzykować użycie przybliżonej pochodnej — najlepiej: przybliżonej niskim kosztem. Jednym z pomysłów mogłoby być wyznaczenie przybliżenia pochodnej na podstawie ilorazów różnicowych, zgodnie z poniższym twierdzeniem.
Twierdzenie 10.4 (o różnicowej aproksymacji pochodnej kierunkowej)
Przyjmijmy, że są spełnione założenia standardowe. Niech ![]() będzie ustalonym punktem w
będzie ustalonym punktem w ![]() i niech
i niech ![]() . Niech
. Niech ![]() będzie na tyle małe, by
będzie na tyle małe, by ![]() . Wtedy
. Wtedy
Twierdzenie to gwarantuje więc, że pochodną w kierunku wektora ![]() można aproksymować ilorazem różnicowym
można aproksymować ilorazem różnicowym
z błędem rzędu ![]() .
.
Dowód
Twierdzenie jest prostą konsekwencją twierdzenia o wartości średniej i założenia lipschitzowskości pochodnej:
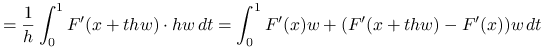 |
|||
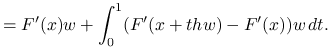 |
Stąd
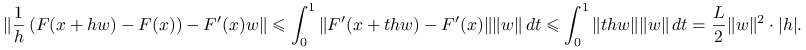 |
Z powyższego wynika pomysł na przybliżenie całej macierzy pochodnej ilorazami różnicowymi: wystarczy wziąć ![]() , gdzie
, gdzie ![]() -ta kolumna
-ta kolumna ![]() ,
, ![]() , jest wyznaczona jako iloraz różnicowy
, jest wyznaczona jako iloraz różnicowy
Twierdzenie 10.5 (o zbieżności metody z pochodną przybliżoną ilorazami różnicowymi)
Przy standardowych założeniach, istnieją dodatnie ![]() i
i ![]() (dostatecznie małe) takie, że jeśli
(dostatecznie małe) takie, że jeśli ![]() jest ciągiem takim, że
jest ciągiem takim, że ![]() oraz
oraz ![]() , to ciąg zdefiniowany wzorem
, to ciąg zdefiniowany wzorem
w którym kolumny macierzy ![]() zadane są ilorazami różnicowymi:
zadane są ilorazami różnicowymi:
jest dobrze określony i zbieżny przynajmniej liniowo do ![]() . Co więcej,
. Co więcej,
jeśli
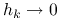 , to
, to 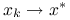 superliniowo;
superliniowo;jeśli
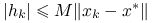 dla pewnej stałej
dla pewnej stałej 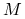 , to
, to 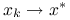 przynajmniej kwadratowo;
przynajmniej kwadratowo;jeśli
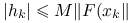 dla pewnej stałej
dla pewnej stałej 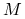 , to
, to 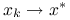 przynajmniej kwadratowo.
przynajmniej kwadratowo.
Dowód
Dla wygody, dowód poprowadzimy w normie ![]() — tzw. kolumnowej normie macierzowej (w przestrzeni skończenie wymiarowej i tak wszystkie normy są równoważne). Mamy więc
— tzw. kolumnowej normie macierzowej (w przestrzeni skończenie wymiarowej i tak wszystkie normy są równoważne). Mamy więc
oraz
Tymczasem, na mocy lematu o różnicowej aproksymacji pochodnej,
Oznaczmy ![]() , wtedy
, wtedy ![]() . Na mocy twierdzenia o lokalnej stabilności metody Newtona z (dla
. Na mocy twierdzenia o lokalnej stabilności metody Newtona z (dla ![]() dostatecznie małych) mamy, że
dostatecznie małych) mamy, że ![]() jest nieosobliwa oraz zachodzi
jest nieosobliwa oraz zachodzi
Stąd już wynika teza twierdzenia. Ostatni warunek kwadratowej zbieżności wynika z oszacowania residuum przez błąd,
gdy tylko ![]() jest dostatecznie blisko
jest dostatecznie blisko ![]() .
.
10.2.4. Niedokładna metoda Newtona
Jak pamiętamy, najkosztowniejszą częścią jednej iteracji Newtona jest rozwiązywanie układu równań z macierzą pochodnej. Alternatywą dla metody bezpośredniej rozwiązywania równania poprawki
mogłaby być, zwłaszcza w przypadku gdy ![]() jest duże, metoda iteracyjna (mielibyśmy zatem do czynienia z iteracją wewnątrz iteracji). Na
jest duże, metoda iteracyjna (mielibyśmy zatem do czynienia z iteracją wewnątrz iteracji). Na ![]() -tym kroku metody Newtona moglibyśmy zatrzymywać wewnętrzną iterację stosując np. residualne kryterium stopu z parametrem wymuszającym
-tym kroku metody Newtona moglibyśmy zatrzymywać wewnętrzną iterację stosując np. residualne kryterium stopu z parametrem wymuszającym ![]() ,
,
Taką modyfikację metody Newtona nazywa się niedokładną metodą Newtona.
Twierdzenie 10.6 (o błędzie niedokładnej metody Newtona)
Przy standardowych założeniach, istnieją dodatnie stałe ![]() i
i ![]() takie, że jeśli
takie, że jeśli ![]() oraz
oraz ![]() spełnia warunek
spełnia warunek
to następna iteracja niedokładnej metody Newtona dana wzorem
spełnia
Dowód
Niech ![]() będzie na tyle małe, by zachodził lemat 9.2 o oszacowaniu funkcji i pochodnej, a także by zachodziło twierdzenie 9.3 o zbieżności metody Newtona z punktem startowym
będzie na tyle małe, by zachodził lemat 9.2 o oszacowaniu funkcji i pochodnej, a także by zachodziło twierdzenie 9.3 o zbieżności metody Newtona z punktem startowym ![]() . Aby udowodnić twierdzenie, najpierw postaramy się wyłuskać związek pomiędzy naszą metodą, a prawdziwą metodą Newtona (o której już sporo wiemy). Mamy bowiem
. Aby udowodnić twierdzenie, najpierw postaramy się wyłuskać związek pomiędzy naszą metodą, a prawdziwą metodą Newtona (o której już sporo wiemy). Mamy bowiem
gdzie ![]() jest residuum rozwiązania równania na poprawkę,
jest residuum rozwiązania równania na poprawkę,
Stąd wynika, że
i konsekwentnie
Ponieważ na mocy twierdzenia o zbieżności metody Newtona mamy ![]() , to wystarczy oszacować ostatni człon nierówności. Z definicji
, to wystarczy oszacować ostatni człon nierówności. Z definicji ![]() mamy
mamy
(W ostatniej nierówności skorzystaliśmy z lematu o oszacowaniu funkcji i pochodnej.)
∎W powyższym dowodzie dostaliśmy rezultat, w którym stała ![]() w oszacowaniu błędu zależała od uwarunkowania
w oszacowaniu błędu zależała od uwarunkowania ![]() , skąd moglibyśmy wysnuć wniosek, że jeśli
, skąd moglibyśmy wysnuć wniosek, że jeśli ![]() jest źle uwarunkowana, to
jest źle uwarunkowana, to ![]() należy brać patologicznie małe. W rzeczywistości nie jest aż tak źle i można osłabić założenia na ciąg
należy brać patologicznie małe. W rzeczywistości nie jest aż tak źle i można osłabić założenia na ciąg ![]() , ale pod warunkiem zmiany normy, w której badamy błąd, tak, by uwzględniać zachowanie się pochodnej:
, ale pod warunkiem zmiany normy, w której badamy błąd, tak, by uwzględniać zachowanie się pochodnej: ![]() (zob. [9]).
(zob. [9]).
Wniosek 10.1 (twierdzenie o zbieżności niedokładnej metody Newtona)
Przy standardowych założeniach, istnieją ![]() i
i ![]() (dostatecznie małe) takie, że jeśli
(dostatecznie małe) takie, że jeśli ![]() oraz
oraz ![]() to niedokładna metoda Newtona z parametrem wymuszającym
to niedokładna metoda Newtona z parametrem wymuszającym ![]() jest zbieżna przynajmniej liniowo do
jest zbieżna przynajmniej liniowo do ![]() . Ponadto,
. Ponadto,
jeśli
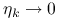 , to zbieżność jest superliniowa;
, to zbieżność jest superliniowa;jeśli
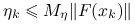 dla pewnego ustalonego
dla pewnego ustalonego 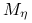 , to zbieżność jest przynajmniej kwadratowa.
, to zbieżność jest przynajmniej kwadratowa.
Ćwiczenie 10.6
Udowodnij powyższy wniosek.
Niedokładna metoda Newtona jest bardzo popularną metodą w przypadku, gdy ![]() jest bardzo duże: wówczas trudno myśleć o sposobach rozwiązywania równania poprawki innych niż jakaś metoda iteracyjna. Dodatkowym plusem tej metody jest to, że znakomicie można ją łączyć z przybliżaniem pochodnej kierunkowej ilorazami różnicowymi; rzeczywiście, głównym składnikiem metody iteracyjnej jest mnożenie
jest bardzo duże: wówczas trudno myśleć o sposobach rozwiązywania równania poprawki innych niż jakaś metoda iteracyjna. Dodatkowym plusem tej metody jest to, że znakomicie można ją łączyć z przybliżaniem pochodnej kierunkowej ilorazami różnicowymi; rzeczywiście, głównym składnikiem metody iteracyjnej jest mnożenie ![]() , co można tanio przybliżać w sposób opisany w rozdziale 10.2.3. W ten sposób oszczędzamy na kilku polach na raz:
, co można tanio przybliżać w sposób opisany w rozdziale 10.2.3. W ten sposób oszczędzamy na kilku polach na raz:
nie musimy wykonywać, zazwyczaj bardzo kosztownego, rozkładu macierzy pochodnej;
nie musimy nawet wyznaczać macierzy pochodnej, lecz w zamian wystarczy, że w każdej wewnętrznej iteracji, jedną dodatkową wartość
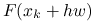 ;
;ponieważ po kilku iteracjach zbliżamy się do rozwiązania, że
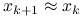 , w ten sposób od razu dysponujemy dobrym przybliżeniem startowym dla iteracji wewnętrznej: w sprzyjających okolicznościach metody Kryłowa mogą z tego zrobić dodatkowy pożytek;
, w ten sposób od razu dysponujemy dobrym przybliżeniem startowym dla iteracji wewnętrznej: w sprzyjających okolicznościach metody Kryłowa mogą z tego zrobić dodatkowy pożytek;możemy ograniczyć koszt rozwiązywania układu z macierzą pochodnej (liczbę iteracji wewnętrznych), stosując łagodne kryterium stopu, gdy jesteśmy daleko od rozwiązania.
Przykład 10.1 (Numeryczne eksperymenty z wariantami metody Newtona dla równania Allena–Cahna)
Porównamy jakość pracy kilku metod:
klasycznej metody Newtona
uproszczonej metody Newtona
metody Szamańskiego o
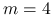 krokach
krokachmetody Newtona z pochodną przybliżoną ilorazami różnicowymi (ze stałym, ale bardzo małym krokiem,
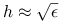 , gdzie
, gdzie 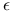 to precyzja arytmetyki.
to precyzja arytmetyki.
Do porównania wybierzemy:
wykresy uzyskanego rozwiązania,
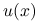 , dla każdej z metod
, dla każdej z metodwykresy residuum,
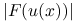 , dla każdej z metod
, dla każdej z metodhistorię zbieżności metody,
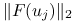
liczbę iteracji, czas pracy, końcową wartość residuum.
Zwróć uwagę na to, że odpowiednio dobierając częstość uaktualniania macierzy pochodnej, można znacząco poprawić efektywność metody (w porównaniu do metody Newtona). Z drugiej strony, zbyt rzadka aktualizacja może przeszkodzić w uzyskaniu zbieżności, jak to dzieje się w naszym przykładzie w przypadku uproszczonej metody Newtona.
Ćwiczenie 10.7
Sprawdź, jak zmienią się wyniki (uzyskane rozwiązanie, jego dokładność, a także — koszt metody i szybkość jej zbieżności), gdy zmienisz jeden z poniższych parametrów
osłabisz nieliniowość, biorąc
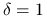 ,
,nieco wzmocnisz nieliniowość, biorąc
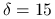 ,
,zwiększysz rozmiar zadania
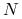 do 400,
do 400,zmniejszysz
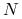 do 20,
do 20,zmniejszysz tolerancję błędu do
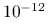 .
.
Zdaje się, że dla ![]() mamy niejednoznaczność rozwiązania? Jak to zweryfikować?
mamy niejednoznaczność rozwiązania? Jak to zweryfikować?
Ćwiczenie 10.8
Zaimplementuj niedokładną metodę Newtona i wykorzystaj ją w skrypcie rozwiązującym (najlepiej: dwuwymiarowe) równanie Allena–Cahna. Jak wpłynęło to na efektywność metody, w porównaniu do standardowej metody Newtona?
Przykład 10.2
Monografii Kelley'a towarzyszy zestaw skryptów, pozwalających przetestować działanie różnych metod iteracyjnych w kilku praktycznych zadaniach [9].
Poniższy skrypt, którego podstawowe kody źródłowe pochodzą ze strony http://www4.ncsu.edu/~ctk/newton, umożliwi Ci zapoznanie się z zadaniem rozwiązania równania Chandrasekhara [9, rozdział 5.6].
Aby w pełni wykorzystać możliwości skryptu, zachęcamy do uruchomienia go na własnym (podłączonym do internetu) komputerze i następnie do wnikliwej obserwacji zmiany wyników przy zmianie, czy to parametrów zadania, czy to parametrów pracy solvera.




