Zagadnienia
13. Kwadratury interpolacyjne w wielu wymiarach
13.1. Sformułowanie zadania
Ostatnie trzy wykłady poświęcimy numerycznemu całkowaniu funkcji
wielu zmiennych. Dokładniej, dla danej funkcji ![]() chcemy obliczyć (przybliżyć) wartość
chcemy obliczyć (przybliżyć) wartość
![I_{d}(f)\,=\,\int _{{[0,1]^{d}}}f(\vec{x})\, d\vec{x}\;=\;\underbrace{\int _{0}^{1}\int _{0}^{1}\cdots\int _{0}^{1}}_{d}\, f(x_{1},x_{2},\ldots,x_{d})\, dx_{1}dx_{2}\cdots dx_{d}.](wyklady/mo2/mi/mi2368.png) |
Zakładamy, że powyższa całka istnieje.
W ogólniejszym sformułowaniu, chcielibyśmy obliczyć całkę
z wagą ![]() funkcji
funkcji ![]() , która jest postaci
, która jest postaci
Waga ![]() jest tutaj nieujemna i całkowalna.
jest tutaj nieujemna i całkowalna.
Zauważmy, że ograniczenie się w ostatnim przypadku do ![]() nie zmniejsza ogólności, gdyż całkę po dowolnym mierzalnym
obszarze
nie zmniejsza ogólności, gdyż całkę po dowolnym mierzalnym
obszarze ![]() można wymodelować przyjmując, że
waga
można wymodelować przyjmując, że
waga ![]() dla wszystkich
dla wszystkich ![]() .
.
Zadanie całkowania funkcji wielu zmiennych ma ogromne znaczenie praktyczne i dlatego warto znać skuteczne metody numeryczne jego rozwiązywania.
Przykład 13.1
Wycena obecnej wartości wielu instrumentów finansowych, w tym
tzw. opcji, opiera się na założeniu, że przyszłe ceny podlegają
losowym zmianom kolejnych odcinkach czasowych. Obecna wartość
opcji obliczana jest jako wartość oczekiwana funkcji wypłaty.
Odpowiada to obliczaniu całki oznaczonej funkcji ![]() zmiennych,
gdzie
zmiennych,
gdzie ![]() jest liczbą odciników czasowych. Jest to często całka
ze standardową
jest liczbą odciników czasowych. Jest to często całka
ze standardową ![]() wymiarową wagą gaussowską postaci
wymiarową wagą gaussowską postaci
przy czym ![]() jest (zwykle skomplikowaną) funkcją wypłaty na
końcu okresu, a
jest (zwykle skomplikowaną) funkcją wypłaty na
końcu okresu, a ![]() reprezentują czynniki losowe w kolejnych
odcinkach czasu. Wymiar
reprezentują czynniki losowe w kolejnych
odcinkach czasu. Wymiar ![]() może wynosić nawet kilka tysięcy.
może wynosić nawet kilka tysięcy.
Z podstawowego wykładu z metod numerycznych każdy z nas wie jak numerycznie całkować funkcje jednej zmiennej. Stosowane metody w znakomitej większości przypadków sprowadzają się do scałkowania funkcji, która jest kawałkami wielomianem określonego stopnia interpolującym funkcję podcałkową. Pomysł ten może być uogólniony na przypadek funkcji wielu zmiennych. Aby jednak mówić o kwadraturach interpolacyjnych w wielu wymiarach, musimy najpierw zastanowić się nad rozwiązywalnością odpowiedniego zadania interpolacyjnego.
13.2. Interpolacja na siatkach regularnych
13.2.1. Postać wielomianu interpolacyjnego
Niech
Jeśli ![]() jest funkcją jednej zmiennej,
jest funkcją jednej zmiennej, ![]() , to wielomian
, to wielomian
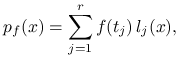 |
gdzie ![]() jest
jest ![]() -tym wielomianem Lagrange'a,
-tym wielomianem Lagrange'a,
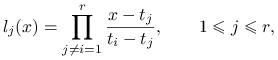 |
(przy czym ![]() dla
dla ![]() )
jest stopnia co najwyżej
)
jest stopnia co najwyżej ![]() i interpoluje
i interpoluje ![]() w punktach
w punktach ![]() ,
tzn. przyjmuje w tych punktach te same wartości co
,
tzn. przyjmuje w tych punktach te same wartości co ![]() . W przypadku
. W przypadku
![]() możemy podobnie zdefiniować ,,wielowymiarowe” wielomiany Lagrange'a.
możemy podobnie zdefiniować ,,wielowymiarowe” wielomiany Lagrange'a.
W tym celu zakładamy, że na każdej współrzędnej dany jest przedział,
a w nim układ ![]() punktów
punktów
Oznaczając przez ![]() odpowiednie wielomiany Lagrange'a jednej zmiennej
dla
odpowiednie wielomiany Lagrange'a jednej zmiennej
dla ![]() -tego podziału, definiujemy wielomiany Lagrange'a
-tego podziału, definiujemy wielomiany Lagrange'a ![]() zmiennych jako
zmiennych jako
dla wszystkich ![]() ,
, ![]() . Dla skrócenia zapisu,
będziemy dalej używać zapisu wektorowego
. Dla skrócenia zapisu,
będziemy dalej używać zapisu wektorowego ![]() ,
a
,
a ![]() będzie oznaczać, że nierówności zachodzą
dla każdej współrzędnej
będzie oznaczać, że nierówności zachodzą
dla każdej współrzędnej ![]() ,
, ![]() . Podobnie,
. Podobnie,
![]() .
.
Wielomiany ![]() należą do przestrzeni
należą do przestrzeni ![]() wielomianów
wielomianów ![]() zmiennych postaci
zmiennych postaci
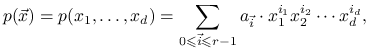 |
gdzie ![]() są dowolnymi wsoółczynnikami rzeczywistymi.
Zauważmy, że
są dowolnymi wsoółczynnikami rzeczywistymi.
Zauważmy, że ![]() wtedy i tylko wtedy gdy
wtedy i tylko wtedy gdy ![]() jest wielomianem stopnia co najwyżej
jest wielomianem stopnia co najwyżej ![]() ze względu na każdą
zmienną
ze względu na każdą
zmienną ![]() .
.
Lemat 13.1
Jeśli wielomian ![]() zeruje się we wszystkich
zeruje się we wszystkich
![]() punktach
punktach ![]() ,
, ![]() , to
, to ![]() jest wielomianem
zerowym.
jest wielomianem
zerowym.
Dowód
Dowód przeprowadzimy przez indukcję ze względu na wymiar ![]() .
Dla
.
Dla ![]() lemat jest oczywiście prawdziwy, bo na podstawie
zasadniczego twierdzenia algebry niezerowy wielomian stopnia
co najwyżej
lemat jest oczywiście prawdziwy, bo na podstawie
zasadniczego twierdzenia algebry niezerowy wielomian stopnia
co najwyżej ![]() nie może mieć
nie może mieć ![]() różnych zer.
różnych zer.
Niech ![]() . Niech
. Niech ![]() będą współczynnikami
wielomianu
będą współczynnikami
wielomianu ![]() . Dla ustalonej
. Dla ustalonej ![]() zdefiniujmy wielomian
zdefiniujmy wielomian
![]() jako
jako
Wielomian ten zeruje się w ![]() punktach
punktach
![]() . Zapisując go w postaci
. Zapisując go w postaci
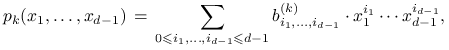 |
gdzie współczynniki
oraz stosując założenie indukcyjne mamy, że
![]() . A więc dla wszystkich wyborów
indeksów
. A więc dla wszystkich wyborów
indeksów ![]() wielomian jednej zmiennej
wielomian jednej zmiennej
![]() zeruje się w
zeruje się w ![]() punktach
punktach ![]() . To zaś wymusza
. To zaś wymusza ![]() dla wszystkich
dla wszystkich ![]() i w konsekwencji
i w konsekwencji ![]() .
.
Lemat 13.1 wykorzystamy do pokazania następującego twierdzenia.
Twierdzenie 13.1
Wielomiany ![]() ,
, ![]() , tworzą bazę
przestrzeni
, tworzą bazę
przestrzeni ![]() . W szczególności,
. W szczególności,
![]() .
.
Dowód
Zauważmy, że podobnie jak w przypadku ![]() ,
,
Stąd, jeśli kombinacja liniowa
![]() jest wielomianem
zerowym to dla wszystkich
jest wielomianem
zerowym to dla wszystkich ![]()
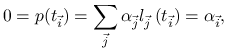 |
czyli układ ![]() jest liniowo
niezależny. Z drugiej strony, układ ten rozpina
jest liniowo
niezależny. Z drugiej strony, układ ten rozpina ![]() ,
bo dla dowolnego wielomianu
,
bo dla dowolnego wielomianu ![]() z tej przestrzeni mamy
z tej przestrzeni mamy
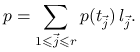 |
(13.1) |
Rzeczywiście, w przeciwnym przypadku różnica wielomianu ![]() i prawej strony (13.1) byłaby niezerowym wielomianem
w
i prawej strony (13.1) byłaby niezerowym wielomianem
w ![]() , który zeruje się we wszystkich
, który zeruje się we wszystkich ![]() punktach
punktach
![]() . To zaś przczyłoby lematowi 13.1.
. To zaś przczyłoby lematowi 13.1.
Stąd już jeden krok do następującego wniosku podsumowującego nasze dotychczasowe rozważania. Niech
będzie ![]() wymiarowym prostokątem.
wymiarowym prostokątem.
Wniosek 13.1
Dla dowolnej funkcji ![]() wielomian
wielomian
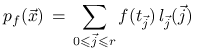 |
jest jedynym wielomianem w ![]() interpolującym
interpolującym ![]() w punktach
w punktach ![]() tzn. takim, że
tzn. takim, że
dla wszystkich ![]() .
.
13.2.2. Błąd interpolacji
Zastanówmy się teraz jaki jest błąd otrzymanej interpolacji.
Dla uproszczenia będziemy od teraz zakładać, że ![]() jest kostką
jest kostką
![]() wymiarową, tzn. wszystkie krawędzie mają tą samą długość,
którą oznaczymy przez
wymiarową, tzn. wszystkie krawędzie mają tą samą długość,
którą oznaczymy przez ![]() , a węzły na każdej współrzędnej
, a węzły na każdej współrzędnej
gdzie
jest pewną ustaloną siatką na odcinku jednostkowym.
W przypadku skalarnym, o ile funkcja ![]() jest
jest ![]() -krotnie
różniczkowalna w sposób ciągły, to
-krotnie
różniczkowalna w sposób ciągły, to
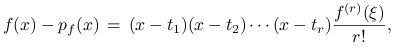 |
przy czym ![]() zależy od
zależy od ![]() . Stąd w szczególności mamy
. Stąd w szczególności mamy
| (13.2) |
gdzie ![]() .
Aby wyprowadzić formułę na bład interpolacji w przypadku
wielowymiarowym, będziemy potrzebować pewnego prostego
uogólnienia ostatniego wzoru.
.
Aby wyprowadzić formułę na bład interpolacji w przypadku
wielowymiarowym, będziemy potrzebować pewnego prostego
uogólnienia ostatniego wzoru.
Załóżmy, że zamiast dokładnych wartości ![]() mamy jedynie
wartości przybliżone
mamy jedynie
wartości przybliżone ![]() takie, że błąd
takie, że błąd
| (13.3) |
Niech dalej ![]() będzie wielomianem stopnia co najwyżej
będzie wielomianem stopnia co najwyżej
![]() interpolującym dane przybliżone
interpolującym dane przybliżone ![]() w punktach
w punktach ![]() .
Ponieważ
.
Ponieważ ![]() jest wielomianem interpolującym dane
jest wielomianem interpolującym dane
![]() , na podstawie wzoru (13.1) mamy
, na podstawie wzoru (13.1) mamy
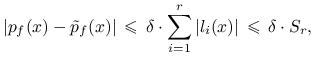 |
gdzie ![]() , a dla
, a dla ![]()
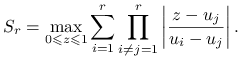 |
Stąd i z formuły na błąd interpolacji dla dokładnych danych otrzymujemy
| (13.4) |
Wprowadzimy jeszcze klasę ![]() funkcji
funkcji
![]() , które w całej swojej dziedzinie są
, które w całej swojej dziedzinie są ![]() -krotnie
różniczkowalne w sposób ciągły ze względu na każdą zmienną.
Dla
-krotnie
różniczkowalne w sposób ciągły ze względu na każdą zmienną.
Dla ![]() definiujemy
definiujemy
Twierdzenie 13.2
Niech ![]() .
Jeśli
.
Jeśli ![]() to dla każdego
to dla każdego ![]() błąd interpolacji
błąd interpolacji
gdzie ![]() , a dla
, a dla ![]()
Dowód
Rozpatrzymy tylko ![]() pozostawiając przypadek
pozostawiając przypadek ![]() jako
proste ćwiczenie.
jako
proste ćwiczenie.
Dla ![]() nierówność w tezie jest równoważna (13.2).
Załóżmy więc, że
nierówność w tezie jest równoważna (13.2).
Załóżmy więc, że ![]() . Ponieważ dla każdego ustalonego
. Ponieważ dla każdego ustalonego
![]() wielomian
wielomian ![]() zmiennych
zmiennych
![]() jest wielomianem interpolacyjnym
dla funkcji
jest wielomianem interpolacyjnym
dla funkcji ![]() zmiennych
zmiennych ![]() ,
na podstawie założenia indukcyjnego mamy
,
na podstawie założenia indukcyjnego mamy
| (13.5) |
Zauważmy, że dla ustalonych z kolei pierwszych ![]() współrzędnych
współrzędnych
![]() wielomian
wielomian ![]() jest
wielomianem jednej zmiennej
jest
wielomianem jednej zmiennej ![]() interpoluącym funkcję jednej
zmiennej
interpoluącym funkcję jednej
zmiennej ![]() w punktach
w punktach ![]() na podstawie
danych zaburzonych na poziomie
na podstawie
danych zaburzonych na poziomie ![]() równym prawej stronie
(13.5). Stąd i z (13.4) ostatecznie otrzymujemy
równym prawej stronie
(13.5). Stąd i z (13.4) ostatecznie otrzymujemy
13.3. Kwadratury interpolacyjne
13.3.1. Kwadratury proste
Jesteśmy już dobrze uzbrojeni w mechanizm interpolacyjny
i możemy zdefiniować wielowymiarowe kwadratury interpolacyjne
dla całkowania funkcji ![]() zdefiniowanych na kostce
zdefiniowanych na kostce
Kwadratury te dane są równością
| (13.6) |
gdzie ![]() jest wielomianem interpolującym
jest wielomianem interpolującym
![]() w punktach
w punktach ![]() ,
, ![]() .
.
Chociaż postać (13.6) kwadratury znakomicie nadaje się do rozważań teoretycznych, nie jest jednak praktyczna ze względu na obliczenia. Zauważmy, że
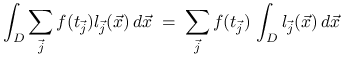 |
||||
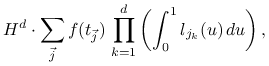 |
gdzie ![]() jest
jest ![]() -tym wielomianem Lagrange'a dla punktów
-tym wielomianem Lagrange'a dla punktów
![]() . Stąd, wprowadzając oznaczenie
. Stąd, wprowadzając oznaczenie
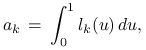 |
kwadraturę interpolacyjną można zapisać w postaci
Zauważmy, że ![]() są współczynnikami jednowymiarowej
kwadratury interpolacyjnej
są współczynnikami jednowymiarowej
kwadratury interpolacyjnej ![]() opartej na punktach
opartej na punktach ![]() , przybliżającej całkę
, przybliżającej całkę
![]() . Mówiąc inaczej, zdefiniowana przez
nas wielowymiarowa kwadratura interpolacyjna jest
. Mówiąc inaczej, zdefiniowana przez
nas wielowymiarowa kwadratura interpolacyjna jest ![]() -produktem
tensorowym wybranej kwadratury jednowymiarowej.
-produktem
tensorowym wybranej kwadratury jednowymiarowej.
Na koniec tego podrozdziału podamy oszacowanie błędu
kwadratury ![]() . Ponieważ
. Ponieważ
z twierdzenia 13.2 natychmiast otrzymujemy następujący wniosek.
Wniosek 13.2
Jeśli ![]() to błąd kwadratury
interpolacyjnej
to błąd kwadratury
interpolacyjnej ![]() jest ograniczony przez
jest ograniczony przez
13.3.2. Kwadratury złożone
Podobnie jak w przypadku funkcji jednej zmiennej, definiujemy
kwadratury złożone dla funkcji wielu zmiennych. Dla uproszczenia
zakładamy, że całkujemy po kostce jednostkowej ![]() .
.
Dla danego ![]() wprowadzamy podział kostki na
wprowadzamy podział kostki na ![]() podkostek
podkostek
Następnie na każdej podkostce stosujemy prostą kwadraturę
interpolacyjną opartą na siatce regularnej składającej się
z ![]() punktów. Skonstruowaną w ten sposób kwadraturę
złożoną oznaczymy przez
punktów. Skonstruowaną w ten sposób kwadraturę
złożoną oznaczymy przez ![]() .
.
Przykład 13.2
Jeśli bazową kwadraturą jednowymiarową jest reguła punktu środkowego,
to wynikową kwadraturą złożoną na ![]() jest
po prostu reguła prostokątów
jest
po prostu reguła prostokątów
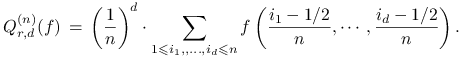 |
Nasze rozważania wieńczy twierdzenie o błędzie kwadratury złożonej, które natychmiast wynika z wniosku 13.2 oraz sposobu konstrukcji kwadratury.
Twierdzenie 13.3
Kwadratura złożona ![]() korzysta z co najwyżej
korzysta z co najwyżej
wartości funkcji ![]() . Jeśli
. Jeśli ![]() to jej błąd
to jej błąd
![\left|\int _{{[0,1]^{d}}}f(\vec{x})\, d\vec{x}\,-\, Q^{{(n)}}_{{r,d}}(f)\right|\,\le\,\left(\frac{1}{N}\right)^{{r/d}}\left(\frac{r^{r}}{r!}\right)\, C_{{r,d}}\, B_{r}(f).](wyklady/mo2/mi/mi2272.png) |
13.4. Przekleństwo wymiaru
Złożone kwadratury interpolacyjne mogą być z powodzeniem
stosowane dla niskich wymiarów, powiedzmy ![]() . Dla dużych
wymiarów
. Dla dużych
wymiarów ![]() mają one bowiem tą niepożądaną własność,
że liczba węzłów rośnie wykładniczo szybko wraz z
zagęszczaniem siatki. Nawet jeśli weźmiemy po
mają one bowiem tą niepożądaną własność,
że liczba węzłów rośnie wykładniczo szybko wraz z
zagęszczaniem siatki. Nawet jeśli weźmiemy po ![]() punkty na
każdej współrzędnej to całkowita liczba punktów siatki
regularnej wyniesie
punkty na
każdej współrzędnej to całkowita liczba punktów siatki
regularnej wyniesie ![]() . Pamiętamy, że w wielu praktycznych
zastosowaniach
. Pamiętamy, że w wielu praktycznych
zastosowaniach ![]() może sięgać nawet kilku tysięcy.
W takich przypadkach obliczenie wartości kwadratury jest
zadaniem praktycznie niewykonalnym.
może sięgać nawet kilku tysięcy.
W takich przypadkach obliczenie wartości kwadratury jest
zadaniem praktycznie niewykonalnym.
To jednak nie koniec złych wiadomości. Przyjrzyjmy się
jeszcze błędowi złożonej kwadratury interpolacyjnej.
Twierdzenie 13.3 mówi, że błąd ten jest
ograniczony z góry proporcjonalnie do ![]() , gdzie
, gdzie ![]() jest liczbą wszystkich użytych punktów. To drugi powód
do niepokoju, uzasadniony poniższym przykładem.
jest liczbą wszystkich użytych punktów. To drugi powód
do niepokoju, uzasadniony poniższym przykładem.
Przykład 13.3
Załóżmy, że chcemy całkować funkcję ![]() zmiennych
i jako kwadraturę bazową stosujemy kwadraturę Simpsona,
dla której
zmiennych
i jako kwadraturę bazową stosujemy kwadraturę Simpsona,
dla której ![]() . Górne ograniczenie błędu sugeruje,
że aby być pewnym wyniku z dokładnością
. Górne ograniczenie błędu sugeruje,
że aby być pewnym wyniku z dokładnością ![]() to
musimy obliczyć wartości funkcji w aż
to
musimy obliczyć wartości funkcji w aż ![]() punktach.
Czy naprawdę jest aż tak źle?
punktach.
Czy naprawdę jest aż tak źle?
Rzeczywiście jest tak źle, a nawet gorzej. Okazuje się, że
rzędu zbieżości ![]() nie da się poprawić w klasie funkcji
nie da się poprawić w klasie funkcji
![]() . Mówi o tym następujące twierdzenie.
. Mówi o tym następujące twierdzenie.
Twierdzenie 13.4
Istnieje ![]() o następującej własności.
Dla dowolnej aproksymacji całki wykorzystującej
o następującej własności.
Dla dowolnej aproksymacji całki wykorzystującej ![]() wartości funkcji
można znaleźć funkcję
wartości funkcji
można znaleźć funkcję ![]() dla której
dla której
![]() , a błąd aproksymacji całki wynosi co najmniej
, a błąd aproksymacji całki wynosi co najmniej ![]() .
.
Dowód
Załóżmy, że dana aproksymacja całki oblicza wartości
funkcji w punktach ![]() ,
, ![]() . Dowód twierdzenia
polega na konstrukcji dwóch funkcji,
. Dowód twierdzenia
polega na konstrukcji dwóch funkcji, ![]() i
i ![]() , które
zerują się we wszystkich
, które
zerują się we wszystkich ![]() (a tym samym ich całki
są aproksymowane tą samą liczbą), dla których
(a tym samym ich całki
są aproksymowane tą samą liczbą), dla których
![]() , ale różnica całek
, ale różnica całek
dla pewnej ![]() niezależnej od
niezależnej od ![]() i
i ![]() . Wtedy, przynajmniej
dla jednej z tych funkcji błąd aproksymacji całki wynosi
co najmniej
. Wtedy, przynajmniej
dla jednej z tych funkcji błąd aproksymacji całki wynosi
co najmniej ![]() .
.
Wybierzmy ![]() taką, że
taką, że ![]() i skonstruujmy na
i skonstruujmy na ![]() regularną
siatkę składającą się z
regularną
siatkę składającą się z ![]() kostek, każda o krawędzi
długości
kostek, każda o krawędzi
długości ![]() .
.
Niech dalej ![]() będzie dowolną funkcją
będzie dowolną funkcją ![]() -krotnie
różniczkowalną w sposób ciągły spełniającą
następujące warunki:
-krotnie
różniczkowalną w sposób ciągły spełniającą
następujące warunki:
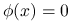 dla
dla 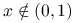 ,
,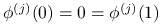 dla
dla 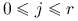 ,
,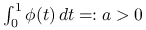 .
.
Każdej kostce
naszej regularnej siatki przyporządkujemy funkcję
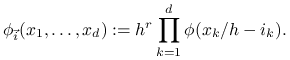 |
Zauważmy, że ![]() oraz
oraz
Jasne jest, że istnieje co najmniej ![]() multi-indeksów
multi-indeksów ![]() (kostek) takich, że żaden z punktów
(kostek) takich, że żaden z punktów
![]() nie należy do wnętrza
nie należy do wnętrza ![]() . Oznaczmy zbiór
takich indeksów przez
. Oznaczmy zbiór
takich indeksów przez ![]() i zdefiniujmy funkcje
i zdefiniujmy funkcje
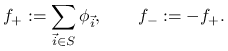 |
Wtedy obie funkcje zerują się w ![]() ,
,
![]() , oraz
, oraz
Podstawiając ![]() dostajemy
ostatecznie
dostajemy
ostatecznie
![\int _{{[0,1]^{d}}}f_{+}(\vec{t})\, d\vec{t}\,\ge\, c\, N^{{-r/d}},\qquad\mbox{gdzie}\quad c=\frac{da^{d}}{r2^{{r+d}}(1+d/r)^{{1+r/d}}}.](wyklady/mo2/mi/mi2395.png) |
Opisane zjawisko nosi nazwę przekleństwa wymiaru.




