Zagadnienia
7. Ściskanie macierzy (preconditioning)
Zbieżność wszystkich dotychczas przez nas poznanych metod iteracyjnych projekcji i Kryłowa zależy od własności spektralnych macierzy rozwiązywanego układu. Pojawiające się w zastosowaniach macierze często mają niestety niekorzystne własności spektralne (np. bardzo duży wskaźnik uwarunkowania), przez co metody iteracyjne zbiegają na nich bardzo wolno.
Przykładowo, dla wielokrotnie tu przywoływanej macierzy ![]() -wymiarowego laplasjanu dyskretyzowanego na siatce o
-wymiarowego laplasjanu dyskretyzowanego na siatce o ![]() węzłach, jej współczynnik uwarunkowania rośnie tak szybko z rozmiarem macierzy (jak
węzłach, jej współczynnik uwarunkowania rośnie tak szybko z rozmiarem macierzy (jak ![]() ), że czyni bezsensownym iteracyjne rozwiązywanie takich układów gdy
), że czyni bezsensownym iteracyjne rozwiązywanie takich układów gdy ![]() jest bardzo duże. .
Zgodnie z twierdzeniem o zbieżności CG, musielibyśmy wykonać rzędu
jest bardzo duże. .
Zgodnie z twierdzeniem o zbieżności CG, musielibyśmy wykonać rzędu ![]() iteracji, by dostatecznie zredukować błąd. Jasne jest, że jeśli
iteracji, by dostatecznie zredukować błąd. Jasne jest, że jeśli ![]() , to koszt iteracji staje się zaporowy, a w międzyczasie dodatkowo mogą odezwać się problemy związane z realizacją iteracji w arytmetyce skończonej precyzji.
, to koszt iteracji staje się zaporowy, a w międzyczasie dodatkowo mogą odezwać się problemy związane z realizacją iteracji w arytmetyce skończonej precyzji.
Dlatego bardzo korzystna może być wstępna transformacja układu
z macierzą o niekorzystnych własnościach, do równoważnego układu
| (7.1) |
którego macierz ![]() ma znacznie korzystniejsze własności z punktu widzenia używanej metody iteracyjnej.
ma znacznie korzystniejsze własności z punktu widzenia używanej metody iteracyjnej.
Okazuje się, że w m.in. przypadku macierzy laplasjanu i podobnych, można faktycznie wskazać taką macierz ![]() , że iteracja nie jest wiele droższa, ale za to znacznie szybciej zbieżna. Z drugiej strony, w innych ważnych z punktu widzenia zastosowań problemach, takiej dobrej macierzy
, że iteracja nie jest wiele droższa, ale za to znacznie szybciej zbieżna. Z drugiej strony, w innych ważnych z punktu widzenia zastosowań problemach, takiej dobrej macierzy ![]() wciąż nie umiemy wskazać.
wciąż nie umiemy wskazać.
W przypadku macierzy symetrycznych widzieliśmy, że kluczowe znaczenie dla zbieżności metody miało rozmieszczenie wartości własnych na osi liczbowej: jeśli wartości własne były bardzo rozrzucone po prostej, to uwarunkowanie było bardzo duże i w konsekwencji zbieżność powolna. Aby zbieżność była szybsza, kluczowe jest, by wartości własne ![]() były ciasno upakowane w kilku klastrach (najlepiej — w jednym).
były ciasno upakowane w kilku klastrach (najlepiej — w jednym).
Jeśli więc chcielibyśmy przekształcić macierz tak, by metoda iteracyjna dla ![]() zbiegała szybko, musimy w jakiś sposób ,,ścisnąć” spektrum macierzy
zbiegała szybko, musimy w jakiś sposób ,,ścisnąć” spektrum macierzy ![]() . Taką operację nazywamy więc ściskaniem (ang. preconditioning — bo zmiana uwarunkowania), a macierz
. Taką operację nazywamy więc ściskaniem (ang. preconditioning — bo zmiana uwarunkowania), a macierz ![]() — macierzą ściskającą.
— macierzą ściskającą.
Aby całość miała sens, macierz ściskająca ![]() powinna być tak dobrana, by jednocześnie zachodziło kilka nieco przeciwstawnych warunków:
powinna być tak dobrana, by jednocześnie zachodziło kilka nieco przeciwstawnych warunków:
macierz
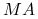 powinna mieć znacznie korzystniejsze własności z punktu widzenia szybkości zbieżności (i ostatecznego kosztu) używanej metody iteracyjnej,
powinna mieć znacznie korzystniejsze własności z punktu widzenia szybkości zbieżności (i ostatecznego kosztu) używanej metody iteracyjnej,macierz
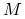 powinna być łatwa w ,,konstrukcji”7W metodach operatorowych (matrix–free) nie jest nam potrzebna macierz
powinna być łatwa w ,,konstrukcji”7W metodach operatorowych (matrix–free) nie jest nam potrzebna macierz 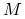 , tylko sposób obliczania
, tylko sposób obliczania 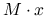 , więc to ta operacja w praktyce wymaga ,,konstrukcji”. Doskonałym przykładem byłoby
, więc to ta operacja w praktyce wymaga ,,konstrukcji”. Doskonałym przykładem byłoby 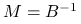 , gdzie
, gdzie 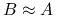 ; wtedy
; wtedy 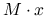 to obliczenie rozwiązania układu równań z macierzą
to obliczenie rozwiązania układu równań z macierzą 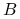 , więc ,,konstrukcją”
, więc ,,konstrukcją” 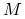 byłoby znalezienie rozkładu LU macierzy
byłoby znalezienie rozkładu LU macierzy 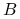 .,
.,macierz
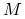 powinna być tania w mnożeniu przez wektor (głównym elementem każdej metody iteracyjnej jest mnożenie macierzy przez wektor: tutaj mamy
powinna być tania w mnożeniu przez wektor (głównym elementem każdej metody iteracyjnej jest mnożenie macierzy przez wektor: tutaj mamy 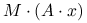 ).
).
Kilka ekstremalnych propozycji na macierz ściskającą to ![]() (łatwa w
konstrukcji i tania w mnożeniu, ale niestety nic nie polepsza…) oraz
(łatwa w
konstrukcji i tania w mnożeniu, ale niestety nic nie polepsza…) oraz
![]() (rewelacyjnie poprawia szybkość zbieżności metody iteracyjnej, dając zbieżność
w jednej iteracji, ale jest droga w mnożeniu i bardzo droga w konstrukcji). Ponieważ obie skrajności są — ze zrozumiałych względów — nie do zaakceptowania, widać więc, że należy poszukiwać czegoś pośredniego: czegoś, co niskim kosztem przybliża (w jakimś sensie) działanie macierzy odwrotnej.
(rewelacyjnie poprawia szybkość zbieżności metody iteracyjnej, dając zbieżność
w jednej iteracji, ale jest droga w mnożeniu i bardzo droga w konstrukcji). Ponieważ obie skrajności są — ze zrozumiałych względów — nie do zaakceptowania, widać więc, że należy poszukiwać czegoś pośredniego: czegoś, co niskim kosztem przybliża (w jakimś sensie) działanie macierzy odwrotnej.
Uogólnieniem ściskania lewostronego (7.1) jest ściskanie obustronne:
| (7.2) | ||||
| (7.3) |
(jeśli powyżej ![]() , to ściskanie jest oczywiście tylko prawostronne).
, to ściskanie jest oczywiście tylko prawostronne).
7.1. Proste operatory ściskające
Jednym z powszechniej stosowanych (aczkolwiek nie zawsze dostatecznie skutecznych) sposobów ściskania są te oparte na zastosowaniu jednego kroku klasycznej metody iteracyjnej (lub jej wersji blokowej). Ponieważ mogą one być stosowane zarówno w wersji lewostronnej (jako ![]() ) lub prawostronnej (jako
) lub prawostronnej (jako ![]() ), operator
), operator ![]() w przykładach poniżej, o ile nie zaznaczono inaczej, będzie mógł oznaczać zarówno
w przykładach poniżej, o ile nie zaznaczono inaczej, będzie mógł oznaczać zarówno ![]() jak i
jak i ![]() .
.
Ściskanie metodą Jacobiego
Ściskanie metodą Jacobiego możemy zastosować tylko wtedy, gdy ![]() dla wszystkich
dla wszystkich ![]() . Wtedy — przez analogię do metody iteracyjnej Jacobiego — wybieramy
. Wtedy — przez analogię do metody iteracyjnej Jacobiego — wybieramy ![]() . Oprócz zasadniczej wady, jaką jest najczęściej kiepska skuteczność w redukcji uwarunkowania, ściskanie metodą Jacobiego ma poza tym wiele zalet:
. Oprócz zasadniczej wady, jaką jest najczęściej kiepska skuteczność w redukcji uwarunkowania, ściskanie metodą Jacobiego ma poza tym wiele zalet:
generowanie
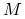 jest praktycznie darmowe,
jest praktycznie darmowe,mnożenie przez
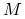 jest bardzo tanie (
jest bardzo tanie (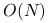 flopów), a przy tym pięknie się zrównolegla.
flopów), a przy tym pięknie się zrównolegla.
Metody niepełnego rozkładu
Inne sposoby ściśnięcia macierzy obejmują np. techniki tzw. niepełnego
rozkładu macierzy. Ich idea opiera się na obserwacji, że ,,idealną” macierzą ściskającą byłaby ![]() . Przypomnijmy, że w takim przypadku mnożenie
. Przypomnijmy, że w takim przypadku mnożenie ![]() najlepiej wykonać, gdy zawczasu wyznaczymy czynniki rozkładu
najlepiej wykonać, gdy zawczasu wyznaczymy czynniki rozkładu ![]() (co może nas drogo kosztować) i wtedy
(co może nas drogo kosztować) i wtedy ![]() (tu wykorzystamy fakt, że układy równań z macierzami
(tu wykorzystamy fakt, że układy równań z macierzami ![]() i
i ![]() są ,,łatwiejsze” do rozwiązania, bo macierze są trójkątne). Oczywiście, taka ,,idealna” macierz ściskająca ma wadę, która w większości przypadków będzie ją całkowicie dyskwalifikować: mimo, że
są ,,łatwiejsze” do rozwiązania, bo macierze są trójkątne). Oczywiście, taka ,,idealna” macierz ściskająca ma wadę, która w większości przypadków będzie ją całkowicie dyskwalifikować: mimo, że ![]() jest rozrzedzona, macierze
jest rozrzedzona, macierze ![]() i
i ![]() mogą — i zazwyczaj faktycznie są — gęste. Oznacza to, że samo wyznaczenie rozkładu LU macierzy
mogą — i zazwyczaj faktycznie są — gęste. Oznacza to, że samo wyznaczenie rozkładu LU macierzy ![]() będzie nas kosztować zabójcze
będzie nas kosztować zabójcze ![]() flopów.
flopów.
Inżynierski pomysł na usunięcie tej wady jest taki, by w algorytmie wyznaczania czynników rozkładu LU wyznaczać jedynie te elementy ![]() dolnego trójkąta
dolnego trójkąta ![]() oraz
oraz ![]() górnego trójkąta
górnego trójkąta ![]() , dla których
, dla których ![]() . Zatem struktura niezerowych elementów macierzy
. Zatem struktura niezerowych elementów macierzy ![]() będzie powielać strukturę niezerowych elementów
będzie powielać strukturę niezerowych elementów ![]() — a więc dostaniemy w efekcie macierze rzadkie!
— a więc dostaniemy w efekcie macierze rzadkie!
Jeśli więc ogólnie algorytm rozkładu LU (w miejscu, bez wyboru elementu głównego) jest postaci:
| for |
| for |
| |
| end |
| for |
| for |
| |
| end |
| end |
| end |
to niepełny rozkład LU miałby (formalnie) postać:
Niepełny rozkład LU, wersja bazowa
| for |
| for |
| if |
| |
| end |
| end |
| for |
| for |
| if |
| |
| end |
| end |
| end |
| end |
Opisana powyżej technika nosi nazwę niepełnego rozkładu LU (ang. incomplete LU factorization) o zerowym wypełnieniu (ang. zero fill-in), co oznaczamy ILU(0). Warto zwrócić uwagę, że może zdarzyć się, że czynnik ![]() uzyskany niepełnym rozkładem macierzy nieosobliwej sam będzie macierzą osobliwą. Dla pewnych klas macierzy — np. dla tzw. M-macierzy [13] — wiadomo, że niepełny rozkład nie prowadzi do takich degeneracji.
uzyskany niepełnym rozkładem macierzy nieosobliwej sam będzie macierzą osobliwą. Dla pewnych klas macierzy — np. dla tzw. M-macierzy [13] — wiadomo, że niepełny rozkład nie prowadzi do takich degeneracji.
Często rozkład ILU(0) produkuje czynniki LU, dla których ![]() jest tak bardzo odległe od
jest tak bardzo odległe od ![]() , że nie dają one dostatecznie silnego ściśnięcia macierzy
, że nie dają one dostatecznie silnego ściśnięcia macierzy ![]() . Wtedy można zastosować któryś z wariantów niepełnego rozkładu
. Wtedy można zastosować któryś z wariantów niepełnego rozkładu
rozkład z progiem, ILUT (ang. treshold ILU), w którym zerujemy te elementy czynników rozkładu, które spełniają pewien warunek progowy — oględnie mówiąc, warunek ten dotyczy względnej wielkości danego elementu (,,pomijamy małe”);
rozkład według wzorca: w którym wprost wskazujemy, jakie elementy
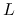 i
i 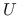 mogą przyjąć niezerowe wartości;
mogą przyjąć niezerowe wartości;rozkład według wypełnienia, ILU(
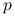 ): w którym dopuszczamy pewne dodatkowe wypełnienie czynników rozkładu.
): w którym dopuszczamy pewne dodatkowe wypełnienie czynników rozkładu.
Szczegółowe omówienie różnych technik niepełnego rozkładu macierzy, razem z ich analizą w niektórych praktycznie użytecznych przypadkach, znajdziemy w monografii Saada [13].
Metody dopasowane do problemu
Najskuteczniejsze operatory ściskające dostajemy wykorzystując do maksimum całą specyfikę konkretnego rozwiązywanego zadania. Na przykład, dla macierzy pochodzących z dyskretyzacji niektórych równań różniczkowych cząstkowych opracowano kilka klas znakomitych sposobów ściskania takich, które gwarantują bardzo szybką zbieżność metod Kryłowa. Wśród nich znajdują się metody dekompozycji obszaru (por. rozdział 5.4, [14], [16], []) oraz metody wielosiatkowe. O tych ostatnich piszemy nieco więcej w rozdziale 8.3.
7.2. Macierze spektralnie równoważne
W wielu zastosowaniach, na przykład w wielokrotnie tu przywoływanych zadaniach dyskretyzacji eliptycznych równań różniczkowych cząstkowych, przedmiotem naszego zainteresowania jest nie tyle jeden układ równań, ale cała ich rodzina,
indeksowana pewnym parametrem ![]() . Rzeczywiście, w przypadku zadań takich jak równanie z macierzą dyskretnego laplasjanu (zob. przykłady 5.1 i 5.2), naszym parametrem
. Rzeczywiście, w przypadku zadań takich jak równanie z macierzą dyskretnego laplasjanu (zob. przykłady 5.1 i 5.2), naszym parametrem ![]() byłby bok oczka siatki dyskretyzacji.
byłby bok oczka siatki dyskretyzacji.
Powstaje więc naturalna potrzeba wskazania klasy macierzy ściskających, których użycie pozwalałoby uzyskać szybkość zbieżności metody iteracyjnej niezależną od ![]() . W przypadku, gdy macierze
. W przypadku, gdy macierze ![]() są symetryczne i dodatnio określone, macierzy ściskających warto szukać w tej samej klasie.
są symetryczne i dodatnio określone, macierzy ściskających warto szukać w tej samej klasie.
Definicja 7.1
Rodzinę macierzy ![]() indeksowaną parametrem
indeksowaną parametrem ![]() nazywamy spektralnie równoważną rodzinie macierzy
nazywamy spektralnie równoważną rodzinie macierzy ![]() , jeśli istnieją dwie stałe
, jeśli istnieją dwie stałe ![]() niezależne od
niezależne od ![]() takie, że
takie, że
| (7.4) |
Ważną własnością macierzy spektralnie równoważnych jest to, że na ich podstawie można skonstruować rodzinę macierzy ściskających, prowadzących do zadania o własnościach spektralnych niezależnych od ![]() , por. [6].
, por. [6].
Twierdzenie 7.1
Jeśli ![]() jest rodziną macierzy spektralnie równoważnych macierzy
jest rodziną macierzy spektralnie równoważnych macierzy ![]() , to wartości własne
, to wartości własne ![]() są ograniczone niezależnie od
są ograniczone niezależnie od ![]() .
.
Dowód
Pokażemy nieco więcej: jeśli zachodzi warunek spektralnej równoważności (7.4), to dla dowolnego ![]()
Ponieważ dla dowolnej macierzy ![]() , jej wartości własne są tożsame z wartościami macierzy
, jej wartości własne są tożsame z wartościami macierzy ![]() , to w szczególności
, to w szczególności ![]() ma spektrum identyczne z macierzą
ma spektrum identyczne z macierzą ![]() . Ta ostatnia jest symetryczna i dodatnio określona, więc wszystkie jej wartości własne są rzeczywiste i dodatnie.
. Ta ostatnia jest symetryczna i dodatnio określona, więc wszystkie jej wartości własne są rzeczywiste i dodatnie.
Podstawiając ![]() w (7.4) i dzieląc stronami przez
w (7.4) i dzieląc stronami przez ![]() dostajemy
dostajemy
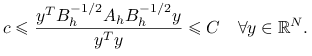 |
Znaczy to, że wartości własne macierzy ![]() leżą w przedziale
leżą w przedziale ![]() .
.
Wynika z twierdzenia Couranta–Fishera.
Jak wiemy z dowodu twierdzenia 7.1, ![]() . Ponieważ wartości własne macierzy odwrotnej są odwrotnościami wartości własnych macierzy danej, to w konsekwencji
. Ponieważ wartości własne macierzy odwrotnej są odwrotnościami wartości własnych macierzy danej, to w konsekwencji
Korzystając z faktu, że iloraz Rayleigh jest ograniczony z góry i z dołu przez ekstremalne wartości własne, dostajemy
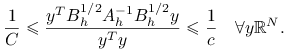 |
Podstawiając ![]() otrzymujemy tezę.
otrzymujemy tezę.
Przykład 7.1 (Wykorzystanie szybkiego solvera do ściśnięcia macierzy dyskretyzacji równania różniczkowego o zmiennych współczynnikach)
Rozważmy eliptyczne równanie różniczkowe
| (7.5) | ||||||
| (7.6) |
gdzie ![]() jest rzeczywistą i symetryczną macierzą rozmiaru
jest rzeczywistą i symetryczną macierzą rozmiaru ![]() , o współczynnikach będących ciągłymi, ograniczonymi funkcjami na
, o współczynnikach będących ciągłymi, ograniczonymi funkcjami na ![]() , spełniającą warunek (gwarantujący eliptyczność w/w równania różniczkowego)
, spełniającą warunek (gwarantujący eliptyczność w/w równania różniczkowego)
Stąd między innymi wynika, że forma dwuliniowa określona na przestrzeni Sobolewa ![]() ,
,
jest ![]() –eliptyczna, to znaczy,
–eliptyczna, to znaczy,
gdzie ![]() . Forma
. Forma ![]() jest także ciągła,
jest także ciągła,
Stałe ![]() zależą oczywiście od
zależą oczywiście od ![]() .
.
Nasze zadanie w postaci wariacyjnej: znaleźć ![]() takie, że
takie, że
będziemy aproksymować metodą elementu skończonego w pewnej podprzestrzeni skończonego wymiaru ![]() (por. wykład z Numerycznych równań różniczkowych). Będziemy więc szukać
(por. wykład z Numerycznych równań różniczkowych). Będziemy więc szukać ![]() takiego, że
takiego, że
Reprezentując8Oczywiście, ![]() zależy od
zależy od ![]() , ale nie będziemy tego wyraźnie zaznaczać, by nie mnożyć indeksów.
, ale nie będziemy tego wyraźnie zaznaczać, by nie mnożyć indeksów. ![]() w bazie
w bazie ![]() przestrzeni
przestrzeni ![]() :
: ![]() mamy, że nasze zadanie dyskretne jest równoważne znalezieniu
mamy, że nasze zadanie dyskretne jest równoważne znalezieniu ![]() spełniającego układ równań
spełniającego układ równań
| (7.7) |
gdzie ![]() . (Macierz
. (Macierz ![]() nazywana jest macierzą sztywności.) Gdy
nazywana jest macierzą sztywności.) Gdy ![]() , metody bezpośrednie mogą być mało efektywne wskutek problemów z wypełnieniem czynników rozkładu, należy więc układ (7.7) rozwiązywać iteracyjnie. Niestety, w przypadku, gdy bazę wybierzemy jako standardową bazę elementu skończonego, macierz
, metody bezpośrednie mogą być mało efektywne wskutek problemów z wypełnieniem czynników rozkładu, należy więc układ (7.7) rozwiązywać iteracyjnie. Niestety, w przypadku, gdy bazę wybierzemy jako standardową bazę elementu skończonego, macierz ![]() jest bardzo źle uwarunkowana ze względu na
jest bardzo źle uwarunkowana ze względu na ![]() :
: ![]() i dlatego konieczne jest solidne jej ściśnięcie.
i dlatego konieczne jest solidne jej ściśnięcie.
Niech ![]() będzie macierzą sztywności uzyskaną w przypadku, gdy
będzie macierzą sztywności uzyskaną w przypadku, gdy ![]() , czyli — ,,zwykłą” macierzą dyskretnego laplasjanu.
, czyli — ,,zwykłą” macierzą dyskretnego laplasjanu.
Zauważmy, że przy zachowaniu wyżej wspomnianej odpowiedniości pomiędzy funkcją ![]() a jej reprezentacją
a jej reprezentacją ![]() w wybranej bazie zachodzi następujący związek pomiędzy macierzą sztywności, a formą dwuliniową:
w wybranej bazie zachodzi następujący związek pomiędzy macierzą sztywności, a formą dwuliniową:
i w konsekwencji także
Na mocy ciągłości i eliptyczności formy ![]() w normie
w normie ![]() , macierze
, macierze ![]() i
i ![]() są spektralnie równoważne.
są spektralnie równoważne.
A więc, znając szybką metodę rozwiązywania zadania z macierzą ![]() — lub, ogólniej, dobrą macierz ściskającą dla
— lub, ogólniej, dobrą macierz ściskającą dla ![]() — dysponujemy jednocześnie dobrym (czytaj: niezależnym od
— dysponujemy jednocześnie dobrym (czytaj: niezależnym od ![]() ) sposobem ściśnięcia macierzy
) sposobem ściśnięcia macierzy ![]() .
.
Aby jednak trochę zbalansować nasz pogląd na tę sprawę warto zauważyć, że swój wkład w uwarunkowanie ![]() ma także stosunek
ma także stosunek ![]() . Jeśli jest on bardzo duży (a może tak być, np. w materiałach silnie anizotropowych), wtedy uwarunkowanie
. Jeśli jest on bardzo duży (a może tak być, np. w materiałach silnie anizotropowych), wtedy uwarunkowanie ![]() — choć już nie będzie zależało od
— choć już nie będzie zależało od ![]() — jednak wciąż będzie wielkie: nad tym, jak najlepiej ściskać takie macierze są obecnie prowadzone badania.
— jednak wciąż będzie wielkie: nad tym, jak najlepiej ściskać takie macierze są obecnie prowadzone badania.
7.3. Metoda PCG
Naturalnym kandydatem na macierz ściskającą w metodzie CG (która jest określona dla macierzy ![]() symetrycznej i dodatnio określonej) jest inna macierz symetryczna i dodatnio określona,
symetrycznej i dodatnio określonej) jest inna macierz symetryczna i dodatnio określona, ![]() . Jak widzieliśmy w twierdzeniu 7.1 i ćwiczeniu 7.2, dobrym kandydatem na
. Jak widzieliśmy w twierdzeniu 7.1 i ćwiczeniu 7.2, dobrym kandydatem na ![]() mogłaby być macierz spektralnie równoważna macierzy
mogłaby być macierz spektralnie równoważna macierzy ![]() . Wydawać by się jednak mogło, że jednostronne (na przykład, lewostronne) ściskanie taką macierzą nie powiedzie się, bo otrzymana przez nas macierz,
. Wydawać by się jednak mogło, że jednostronne (na przykład, lewostronne) ściskanie taką macierzą nie powiedzie się, bo otrzymana przez nas macierz, ![]() , w ogólnosci nie musi być dalej symetryczna — wbrew założeniom uczynionym w wyprowadzeniu metody CG.
, w ogólnosci nie musi być dalej symetryczna — wbrew założeniom uczynionym w wyprowadzeniu metody CG.
Na szczęście, macierz ![]() jest symetryczna, ale w niestandardowym iloczynie skalarnym:
jest symetryczna, ale w niestandardowym iloczynie skalarnym: ![]() . Aby uniknąć przeformułowania wyników uzyskanych we wcześniejszych rozdziałach, użyjemy pewnego triku: teoretycznie użyjemy zadania symetrycznie ściśniętego obustronnie macierzami
. Aby uniknąć przeformułowania wyników uzyskanych we wcześniejszych rozdziałach, użyjemy pewnego triku: teoretycznie użyjemy zadania symetrycznie ściśniętego obustronnie macierzami ![]() :
:
| (7.8) | ||||
| (7.9) |
ale implementację doprowadzimy do takiego stanu, że będzie w niej występować tylko mnożenie wektora przez macierz ![]() — i to tylko jeden raz w każdej iteracji!
— i to tylko jeden raz w każdej iteracji!
Rzeczywiście, ściśnięta macierz ![]() jest symetryczna i dodatnio określona, można więc do niej zastosować bezpośrednio algorytm CG, wyznaczający kolejne przybliżenia
jest symetryczna i dodatnio określona, można więc do niej zastosować bezpośrednio algorytm CG, wyznaczający kolejne przybliżenia ![]() .
Oznaczając
.
Oznaczając ![]() , na
, na ![]() -tej iteracji wyznaczymy:
-tej iteracji wyznaczymy:
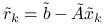 ,
,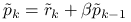
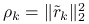
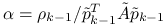
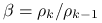
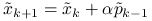
Wprowadzając oznaczenia ![]() , gdzie
, gdzie ![]() , i przyjmując
, i przyjmując ![]() możemy zapisać powyższe operacje wyłącznie w terminach wartości ,,bezfalkowych”:
możemy zapisać powyższe operacje wyłącznie w terminach wartości ,,bezfalkowych”:
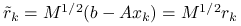 ,
,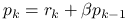 (wynika z pomnożenia odpowiedniej równości z falkami przez
(wynika z pomnożenia odpowiedniej równości z falkami przez 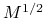 )
)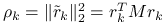
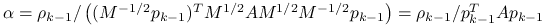
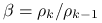
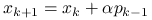 (wynika z pomnożenia odpowiedniej równości z falkami przez
(wynika z pomnożenia odpowiedniej równości z falkami przez 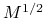 ).
).
Znaczy to, że cały algorytm PCG możemy w praktyce zaimplementować tak, jak algorytm CG z tą różnicą, że do wyznaczenia ![]() będziemy musieli obliczyć dodatkowy wektor
będziemy musieli obliczyć dodatkowy wektor ![]() . Tym samym w implementacji nie pojawi się nigdzie mnożenie przez
. Tym samym w implementacji nie pojawi się nigdzie mnożenie przez ![]() — w każdej iteracji będzie potrzebne tylko jedno mnożenie przez
— w każdej iteracji będzie potrzebne tylko jedno mnożenie przez ![]() !
!
Przykład 7.2
Działanie PCG z dobrą macierzą ściskającą prześledzimy na przykładzie macierzy jednowymiarowego laplasjanu, o losowo zaburzonych elementach:
gdzie ![]() jest symetryczną, trójdiagonalną macierzą o losowo wybranych elementach z przedziału
jest symetryczną, trójdiagonalną macierzą o losowo wybranych elementach z przedziału ![]() (przy czym
(przy czym ![]() jest małe), a
jest małe), a ![]() zadano wzorem (5.5).
zadano wzorem (5.5).
Sprawdź, czy szybkość zbieżności PCG zależy od ![]() i od
i od ![]() . Zobacz, jak zmienią się rezultaty, gdy zaburzenie nie będzie zachowywać symetrii lub dodatniej określoności
. Zobacz, jak zmienią się rezultaty, gdy zaburzenie nie będzie zachowywać symetrii lub dodatniej określoności ![]() . A co stanie się, gdy
. A co stanie się, gdy ![]() nie będzie trójdiagonalna?
nie będzie trójdiagonalna?
Ćwiczenie 7.3
Wykaż, że w metodzie PCG ![]() .
.
Ponieważ ![]() , to mnożąc stronami przez
, to mnożąc stronami przez ![]() mamy, że
mamy, że ![]() . Ponieważ
. Ponieważ
to
7.4. Ściskanie dla GMRES
Ponieważ metoda GMRES nie wymaga żadnych specjalnych własności macierzy (z wyjątkiem nieosobliwości), po obustronnym ściśnięciu9Jednostronne ściśnięcie dostaniemy, biorąc jedną z macierzy równą identyczności. macierzy ![]() nieosobliwymi macierzami
nieosobliwymi macierzami ![]() i
i ![]() :
:
wystarczy do macierzy ![]() zastosować standardowy algorytm GMRES i pamiętać, by wyznaczone rozwiązanie przybliżone
zastosować standardowy algorytm GMRES i pamiętać, by wyznaczone rozwiązanie przybliżone ![]() przetransformować do rozwiązania oryginalnego układu:
przetransformować do rozwiązania oryginalnego układu:
Wszelkie mnożenia przez macierz ściśniętą będziemy oczywiście realizować zgodnie z nawiasami:
Warto pamiętać, GMRES będzie obliczał residua równe ![]() , zatem tylko gdy stosujemy prawostronne ściskanie, residua wyznaczone algorytmem GMRES będą identyczne z residuami układu wyjściowego (co, generalnie, samo w sobie niekoniecznie musi być wartością na której powinno nam zależeć).
, zatem tylko gdy stosujemy prawostronne ściskanie, residua wyznaczone algorytmem GMRES będą identyczne z residuami układu wyjściowego (co, generalnie, samo w sobie niekoniecznie musi być wartością na której powinno nam zależeć).
7.5. Kryteria stopu metod iteracyjnych
Do tej pory zajmowaliśmy się samymi metodami przybliżonego rozwiązywania równań, zwracając uwagę na koszt jednej iteracji, sposób implementacji czy też szybkość zbieżności. Jednak każdą iterację musimy kiedyś w końcu przerwać; musimy więc zadać sobie pytanie: kiedy i na jakiej podstawie powinniśmy zakończyć działanie metody iteracyjnej?
7.5.1. Kryterium błędu
Idealnym kryterium stopu metody iteracyjnej byłaby redukcja błędu poniżej zadanego poziomu, mierzonego w zadanej przez użytkownika normie. Kryterium błędu zatrzymania metody iteracyjnej może więc mieć jedną z trzech postaci:
- Bezwzględne
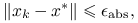
- Względne
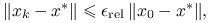
- Mieszane
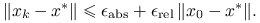
Sęk w tym, że zazwyczaj nie możemy wyznaczyć ![]() z prostego powodu: nie znamy rozwiązania dokładnego
z prostego powodu: nie znamy rozwiązania dokładnego ![]() ! Z drugiej strony, zawsze dysponujemy przecież inną, obliczalną wprost wartością: residuum
! Z drugiej strony, zawsze dysponujemy przecież inną, obliczalną wprost wartością: residuum ![]() .
.
7.5.2. Kryterium residualne
Ponieważ ![]() odpowiada znalezieniu rozwiązania dokładnego, to kryterium stopu możemy oprzeć na redukcji residuum poniżej zadanego poziomu.
Kryterium residualne zatrzymania metody iteracyjnej może więc mieć jedną z trzech postaci:
odpowiada znalezieniu rozwiązania dokładnego, to kryterium stopu możemy oprzeć na redukcji residuum poniżej zadanego poziomu.
Kryterium residualne zatrzymania metody iteracyjnej może więc mieć jedną z trzech postaci:
- Bezwzględne
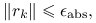
- Względne
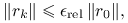
- Mieszane
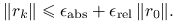
Ćwiczenie 7.4
Podaj przykład takiej normy, w której możemy dokładnie wyznaczyć ![]() na podstawie
na podstawie ![]() .
.
Pamiętajmy, że zakładamy zawsze, że ![]() jest nieosobliwa. Ponieważ
jest nieosobliwa. Ponieważ ![]() , to
, to
Zatem standardowa norma euklidesowa residuum odpowiada normie energetycznej błędu liczonej w normie indukowanej przez macierz symetryczną i dodatnio określoną ![]() .
.
Jednak zależność między normą residuum a tą samą normą błędu może nie być bardzo wyrazista: po raz kolejny może tu dać znać o sobie złe uwarunkowanie macierzy.
Stwierdzenie 7.1 (o oszacowaniu błędu przez residuum)
Niech ![]() będzie rozwiązaniem układu
będzie rozwiązaniem układu ![]() i niech
i niech ![]() dla zadanego
dla zadanego ![]() . Wtedy
. Wtedy
gdzie ![]() .
.
Powyższe stwierdzenie należy interpretować tak, że jedynie w przypadku, gdy macierz ![]() jest dobrze uwarunkowana w danej normie, mała norma residuum jest dobrym indykatorem małej (tej samej) normy błędu. Warto wiedzieć, że w metodzie CG można niskim kosztem (
jest dobrze uwarunkowana w danej normie, mała norma residuum jest dobrym indykatorem małej (tej samej) normy błędu. Warto wiedzieć, że w metodzie CG można niskim kosztem (![]() , gdzie
, gdzie ![]() jest liczbą iteracji) wyznaczyć (coraz lepsze, wraz z postępem iteracji) dolne oszacowanie na spektralny współczynnik uwarunkowania
jest liczbą iteracji) wyznaczyć (coraz lepsze, wraz z postępem iteracji) dolne oszacowanie na spektralny współczynnik uwarunkowania ![]() .
.
7.5.3. Kryterium postępu
W praktyce obliczeniowej stosuje się dwa dodatkowe kryteria stopu metody iteracyjnej
- Stagnacji
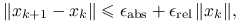
- Cierpliwości
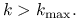
Rzeczywiście, musimy przecież określić moment, kiedy należałoby zakończyć obliczenia, jeśli do tej pory nie przyniosły sukcesu: zrobimy to więc po ![]() iteracjach. Ponadto, jeżeli poprawka
iteracjach. Ponadto, jeżeli poprawka ![]() jest niewielka, to metoda być może na dobre ugrzęzła w jakimś przybliżeniu i wtedy, jeśli nadal jesteśmy daleko od rozwiązania, należałoby spróbować czegoś innego. To kryterium należy stosować z dużym wyczuciem: być może stagnacja metody była tylko chwilowa i po kilku następnych iteracjach zbieżność przyspieszy?
jest niewielka, to metoda być może na dobre ugrzęzła w jakimś przybliżeniu i wtedy, jeśli nadal jesteśmy daleko od rozwiązania, należałoby spróbować czegoś innego. To kryterium należy stosować z dużym wyczuciem: być może stagnacja metody była tylko chwilowa i po kilku następnych iteracjach zbieżność przyspieszy?
Ćwiczenie 7.5
Rozważmy stacjonarną metodę iteracyjną
przy czym ![]() . Wykaż, że jeśli
. Wykaż, że jeśli
to
Ponieważ w metodzie stacjonarnej ![]() , to
, to
Zatem ![]() , skąd teza.
, skąd teza.




