Zagadnienia

9.1 Szybkość zbieżności
9.2 Metoda Banacha
9.3 Metoda Newtona
- 9.3.1 Analiza zbieżności metody Newtona
  - 9.3.1.1 Lematy techniczne
- 9.3.2 Implementacja metody Newtona

9. Układy równań nieliniowych. Metoda Newtona

Zajmiemy się teraz nową, trudniejszą klasą zadań: metodami rozwiązywania układów równań nieliniowych

$F(x)=0,$

gdzie $F:\mathbb{R}^{N}\supset D\rightarrow\mathbb{R}^{N}$ .

W matematyce stosowanej bardzo wiele modeli zyskuje na realizmie, gdy uwzględnić w nich zjawiska nieliniowe. Takie modele są jednak znacznie trudniejsze — zarówno w analizie, jak i w komputerowych symulacjach. Nieustanny wzrost mocy obliczeniowej komputerów, jaki obserwujemy w ciągu ostatnich kilkudziesięciu lat powoduje, że rozwiązywanie dużych układów nawet silnie nieliniowych równań stało się możliwe nawet dla posiadaczy ,,zwykłych” komputerów osobistych.

Od razu zauważmy, że już na poziomie matematycznej poprawności tego zadania możemy napotkać kłopoty, albowiem to zadanie może nie mieć rozwiązań, może mieć dokładnie jedno rozwiązanie, albo skończenie wiele rozwiązań, albo nieskończenie wiele izolowanych rozwiązań, albo… i tak dalej, i tak dalej.

Aby więc szukać jakiegokolwiek rozwiązania powyższego równania, musimy najpierw mieć pewność, że ono istnieje. Nie będziemy się tą kwestią tu zajmować, traktując ją jako domenę matematyki czystej, bez numerycznego zacięcia.

Z kursu Matematyki obliczeniowej I znamy kilka metod rozwiązywania nieliniowego równania skalarnego, $f(x)=0$ : metodę bisekcji, stycznych, siecznych, …. Okazuje się, że niektóre z nich da się w mniej lub bardziej naturalny sposób uogólnić na przypadek wielowymiarowy. W niniejszym rozdziale wyjaśnimy, jak metodę stycznych (Newtona) uogólnić na przypadek wielowymiarowy.

9.1. Szybkość zbieżności

Rozważmy ciąg $(x_{k})\subset\mathbb{R}^{N}$ taki, że $x_{k}\rightarrow x^{*}\in\mathbb{R}^{N}$ gdy $k\rightarrow\infty$ .

Definicja 9.1 (Zbieżność wykładnicza)

Powiemy, że $x_{k}\rightarrow x^{*}$ wykładniczo z rzędem co najmniej $q>1$ , jeśli

$\displaystyle\exists C\geq 0\;\exists K\in\mathbb{N}\quad\| x_{{k+1}}-x^{*}\|\leq C\| x_{{k}}-x^{*}\|^{q}\qquad\forall k\geq K.$

(9.1)

Jeśli wykładnik zbieżności $q=2$ , mówimy wtedy o zbieżności kwadratowej; gdy $q=3$ , zbieżność nazywamy sześcienną (albo: kubiczną). W praktyce, zbieżność kwadratową uznaje się za satysfakcjonująco szybką, a zbieżność kubiczną — za bardzo szybką. Jednak nie zawsze taką szybkość zbieżności można uzyskać; rozsądnym praktycznym minimum jest zbieżność liniowa, w której błąd w każdym kroku maleje o stały czynnik:

Definicja 9.2 (Zbieżność liniowa)

Powiemy, że $x_{k}\rightarrow x^{*}$ przynajmniej liniowo, jeśli

$\exists 0\leq\alpha\leq 1\;\exists K\in\mathbb{N}\quad\| x_{{k+1}}-x^{*}\|\leq\alpha\| x_{{k}}-x^{*}\|\qquad\forall k\geq K.$

Jednak gdy $\alpha\approx 1$ , zbieżność liniowa może być w praktyce nieakceptowalnie wolna.

Oczywiście powyższe nie wyczerpuje wszystkich możliwych szybkości zbieżności. Mianowicie, ciąg może być zbieżny szybciej niż liniowo (choć niekoniecznie zaraz kwadratowo):

Definicja 9.3 (Zbieżność superliniowa)

Powiemy, że $x_{k}\rightarrow x^{*}$ superliniowo, jeśli

$\limsup _{{k\rightarrow\infty}}\dfrac{\| x_{{k+1}}-x^{*}\|}{\| x_{{k}}-x^{*}\|}=0.$

Czasem trudno o samym ciągu powiedzieć, jaki ma wykładnik zbieżności, natomiast łatwiej jest wskazać ciąg o znanym wykładniku zbieżności, który majoryzuje błąd popełniany na każdej iteracji.

Definicja 9.4 (r–zbieżność)

Powiemy, że $x_{k}\rightarrow x^{*}$ r–wykładniczo/r–liniowo/r–superliniowo, jeśli istnieje ciąg $(\xi _{k})\subset\mathbb{R}$ taki, że

$\| x_{{k}}-x^{*}\|\leq\xi _{k}$

oraz $\xi _{k}\rightarrow 0$ , odpowiednio, wykładniczo/liniowo/superliniowo.

Aby móc porównywać (jakościowo) różne metody iteracyjne rozwiązywania równań nieliniowych — o różnych kosztach jednej iteracji i o różnych wykładnikach zbieżności — wprowadza się pojęcie wskaźnika efektywności metody.

Definicja 9.5 (Efektywność metody iteracyjnej)

Wskaźnik efektywności $E$ metody iteracyjnej, zbieżnej wykładniczo z wykładnikiem $q$ , której jedna iteracja kosztuje $m$ flopów, definiujemy jako [17]

$E=q^{{1/m}}.$

Wskaźnik efektywności metody służy szybkiemu jakościowemu porównywaniu metod. Motywacją dla takiej definicji jest wymaganie, by przy zadanym (tym samym) całkowitym koszcie iteracji $W$ obu metod, porównać uzyskane wykładniki redukcji błędu. Jeśli bowiem metoda jest rzędu $q>1$ , to błąd początkowy po $k$ iteracjach zostanie zredukowany do poziomu $\| x_{0}-x^{*}\|^{{q^{k}}}$ . Ponieważ całkowity koszt $k$ iteracji wynosi $W=km$ , to $q^{k}=q^{{W/m}}=(q^{{1/m}})^{W}=E^{W}$ . Definiując w ten sposób efektywność metody iteracyjnej, czynimy jednak pewne oproszczenie, polegające na tym, że pomijamy wpływ stałych na redukcję błędu (patrz oszacowanie (9.1)). Z tego powodu na przykład (formalnie) każda metoda zbieżna liniowo formalnie miałaby taką samą efektywność — równą 1 — choć oczywiście realna sprawność różnych metod liniowych może być różna, m.in. właśnie w zależności od stałej redukcji błędu.

Rozważmy dwa przykłady dużych układów równań nieliniowych, motywowanych — podobnie jak już kilka razy wcześniej w trakcie tego przedmiotu — zadaniami z równań różniczkowych cząstkowych.

Przykład 9.1 (stacjonarne równanie Allena–Cahna)

Rozważmy równanie

		$\displaystyle-\Delta u+\delta u(1-u^{2})=g(x,y)$		$\displaystyle\text{w }\Omega,$
		$\displaystyle u=0$		$\displaystyle\text{na }\partial\Omega.$

Dla uproszczenia przyjmiemy, że $\Omega$ jest kwadratem jednostkowym. Wprowadzając dyskretyzację tego równania najprostszą¹¹Po raz kolejny przypomnijmy, że (z wyjątkiem trywialnych przypadków) najprostsze metody dyskretyzacji, choć bardzo ułatwiają programowanie, to jednak są zwykle najmniej efektywnym sposobem rozwiązywania równań różniczkowych, jeśli wziąć pod uwagę koszt obliczeniowy potrzebny do uzyskania satysfakcjonującego przybliżenia rozwiązania. metodą — metodą różnic skończonych na jednorodnej siatce — patrz przykład 5.2 — otrzymujemy, po uwzględnieniu warunku brzegowego, nieliniowy układ równań algebraicznych,

$P_{N}U_{N}+f(U_{N})=0,$

gdzie $P_{N}$ jest operatorem liniowym zdefiniowanym w przykładzie 5.2, natomiast dla zadanej macierzy $U\in\mathbb{R}^{{N\times N}}$

$(f(U))_{{ij}}=\delta u_{{ij}}(1-u_{{ij}}^{2})-g_{{ij}}.$

(Przypomnijmy, że dokonujemy tutaj utożsamienia macierzy $N\times N$ z wektorem długości $N^{2}$ , ktorego elementami są kolejne wiersze macierzy.)

Przykład 9.2 (ewolucyjne równanie Allena–Cahna)

Rozważmy równanie

		$\displaystyle u_{t}-\Delta u+\delta u(1-u^{2})=g(x,y)$		$\displaystyle\text{w }\Omega,$
		$\displaystyle u=0$		$\displaystyle\text{na }\partial\Omega.$

Dla uproszczenia przyjmiemy, że $\Omega$ jest kwadratem jednostkowym. Wprowadzając dyskretyzację tego równania najprostszą metodą — metodą różnic skończonych na jednorodnej siatce po zmiennej przestrzennej oraz niejawnym schematem Eulera po zmiennej czasowej (patrz wykład z Numerycznych równań różniczkowych, otrzymujemy, po uwzględnieniu warunku brzegowego, nieliniowy układ równań algebraicznych z niewiadomą $U_{N}^{k}$ ,

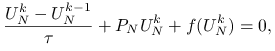$\frac{U_{N}^{k}-U_{N}^{{k-1}}}{\tau}+P_{N}U_{N}^{k}+f(U_{N}^{k})=0,$

gdzie $P_{N}$ jest operatorem liniowym zdefiniowanym w przykładzie 5.2, a $f$ jest zadane jak w poprzednim przykładzie. (Przypomnijmy, że dokonujemy tutaj utożsamienia macierzy $N\times N$ z wektorem długości $N^{2}$ , ktorego elementami są kolejne wiersze macierzy.) Zostawiając po lewej stronie tylko wyrazy z niewiadomymi, dostajemy równanie

$\left(I+\tau P_{N}\right)U_{N}^{k}+\tau f(U_{N}^{k})=U_{N}^{{k-1}},$

a więc takie, w którym — dla dostatecznie małych $\tau$ — część nieliniowa staje się mała w porównaniu z $U_{N}$ .

9.2. Metoda Banacha

Wiele równań nieliniowych można w naturalny sposób sformułować jako zagadnienie punktu stałego,

$x=\Phi(x),$

dla którego najprostszą metodą iteracyjną jest doskonale nam znana metoda Banacha (iteracji prostej),

$x_{{k+1}}=\Phi(x_{k}).$

Przypomnijmy (bez dowodu) twierdzenie o zbieżności tej metody:

Twierdzenie 9.1 (o zbieżności metody Banacha)

Niech $D\subset\mathbb{R}^{N}$ będzie niepusty, ograniczony i domknięty, i niech $\Phi:D\rightarrow D$ będzie kontrakcją, tzn.

$\exists\gamma<1\quad\|\Phi(x)-\Phi(y)\|\leq\gamma\| x-y\|\qquad\forall x,y\in D.$

Wtedy $\Phi$ ma dokładnie jeden punkt stały $x^{*}=\Phi(x^{*})\in D$ oraz dla dowolnego $x_{0}\in D$ iteracja

$x_{{k+1}}=\Phi(x_{k})$

jest zbieżna do $x^{*}$ , przy czym dla każdego $k=0,1,\ldots$ ,

$\| x_{{k+1}}-x^{*}\|\leq\gamma\| x_{{k}}-x^{*}\|.$

Z powyższego twierdzenia wynika więc, że iteracja Banacha jest zbieżna przynajmniej liniowo ze współczynnikiem redukcji błędu $\gamma<1$ .

Przykład 9.3

Stosując niejawny schemat Eulera¹²Por. np. wykład z Numerycznych równań różniczkowych. Podobna metoda — pod nazwą metody łamanych Eulera — bywa wykorzystywana w dowodzie twierdzenia o istnieniu rozwiązania równania różniczkowego. Nas tutaj interesuje ona wyłącznie jako metoda numeryczna.

$y_{{n+1}}=y_{n}+\tau F(t_{{n+1}},y_{{n+1}})$

do przybliżonego rozwiązania układu równań różniczkowych zwyczajnych $y^{{\prime}}(t)=F(t,y)\in\mathbb{R}^{N}$ musimy dla znanego $y_{n}$ znaleźć $y_{{n+1}}$ jako punkt stały odwzorowania

$\Phi(x)=y_{n}+\tau F(t_{{n+1}},x).$

Jeśli $F$ jest lipschitzowska ze stałą $L$ w normie $\|\cdot\|$ ze względu na drugi argument (por. twierdzenie Picarda–Lindelöfa), to

$\|\Phi(x)-\Phi(y)\|=\tau\| F(x)-F(y)\|\leq\tau L\| x-y\|\qquad\forall x,y\in\mathbb{R}^{N},$

zatem $\Phi$ jet kontrakcją na $\mathbb{R}^{N}$ , gdy $\tau L<1$ , czyli gdy krok czasowy $\tau$ schematu Eulera jest dostatecznie mały względem $h$ .

Czasami wygodniej jest skorzystać z ,,lokalnej” wersji twierdzenia o zbieżności metody Banacha:

Twierdzenie 9.2 (o lokalnej zbieżności metody Banacha)

Niech $\Phi:\mathbb{R}^{N}\supset D\rightarrow\mathbb{R}^{N}$ , gdzie $D$ jest otwarty i niepusty, i niech dla zadanego $x_{0}\in D$ istnieje kula $B=\{ x\in\mathbb{R}^{N}:\| x-x_{0}\|\leq r\}$ taka, że $B\subset D$ oraz $\Phi$ jest na $B$ kontrakcją ze stałą $\gamma$ .

Jeśli dodatkowo $\| x_{0}-\Phi(x_{0})\|\leq(1-\gamma)r$ , to w $B$ istnieje dokładnie jeden punkt stały $x^{*}\in B$ odwzorowania $\Phi$ , a metoda iteracji prostej jest doń zbieżna przynajmniej liniowo ze stałą redukcji błędu $\gamma$ .

Dowód

Wystarczy wykazać, że $\Phi(B)\subset B$ i skorzystać z poprzedniego twierdzenia. Na mocy warunku kontrakcji w $B$ , dla $x\in B$ mamy

$\|\Phi(x)-x_{0}\|\leq\|\Phi(x)-\Phi(x_{0})\|+\|\Phi(x_{0})-x_{0}\|\leq\gamma\| x-x_{0}\|+(1-\gamma)r\leq\gamma r+(1-\gamma)r=r,$

zatem faktycznie $\Phi(x)\in B$ .

∎

9.3. Metoda Newtona

W przypadku równania skalarnego, $f:\mathbb{R}\rightarrow\mathbb{R}$ , metoda stycznych (zwana też metodą Newtona) rozwiązywania równania $f(x)=0$ jest zadana wzorem

$x_{{k+1}}=x_{k}-\dfrac{f(x_{k})}{f^{{\prime}}(x_{k})}.$

Przez analogię, gdy $F:\mathbb{R}^{N}\supset D\rightarrow\mathbb{R}^{N}$ można więc byłoby zdefiniować wielowymiarową metodę Newtona wzorem

$\displaystyle x_{{k+1}}=x_{k}-F^{{\prime}}(x_{k})^{{-1}}F(x_{k}),$

(9.2)

gdzie $F^{{\prime}}(x_{k})$ oznaczałoby macierz pochodnej $F$ w punkcie $x_{k}$ . Jak za chwilę się przekonamy, jest to rzeczywiście bardzo dobry pomysł, a tak określona metoda zachowuje (z zachowaniem właściwych proporcji) wszystkie cechy metody Newtona znane nam z przypadku skalarnego!

9.3.1. Analiza zbieżności metody Newtona

Wielowymiarową metodę Newtona i różne jej warianty będziemy analizowali przy pewnych dość ogólnych założeniach dotyczących funkcji $F:\mathbb{R}^{N}\supset D\rightarrow\mathbb{R}^{N}$ . W skrócie, będziemy je nazywali za [9] założeniami standardowymi:

Zbiór 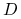$D$ jest otwarty i niepusty, a 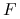$F$ jest różniczkowalna w $D$ .
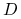Istnieje rozwiązanie $x^{*}\in D$ :

$F(x^{*})=0.$
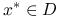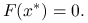
Pochodna 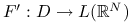$F^{{\prime}}:D\rightarrow L(\mathbb{R}^{N})$ jest lipschitzowska ze stałą $L$ :

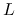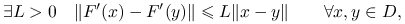
$\exists L>0\quad\| F^{{\prime}}(x)-F^{{\prime}}(y)\|\leq L\| x-y\|\qquad\forall x,y\in D,$

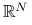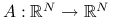przy czym norma po lewej stronie nierówności jest normą operatorową indukowaną przez normę wektorową w $\mathbb{R}^{N}$ obecną po prawej stronie, tzn. dla liniowego operatora $A:\mathbb{R}^{N}\rightarrow\mathbb{R}^{N}$ ,

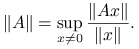
$\| A\|=\sup _{{x\neq 0}}\dfrac{\| Ax\|}{\| x\|}.$
Macierz pochodnej w rozwiązaniu, 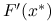$F^{{\prime}}(x^{*})$ , jest nieosobliwa.

9.3.1.1. Lematy techniczne

Przez $K(x^{*},\delta)$ będziemy oznaczali kulę otwartą o środku w $x^{*}$ i promieniu $\delta$ ,

$K(x^{*},\delta)=\{ x\in\mathbb{R}^{N}:\| x-x^{*}\|<\delta\}.$

Lemat 9.1 (użyteczna wersja twierdzenia o wartości średniej)

Niech będą spełnione założenia standardowe i niech $K$ będzie otwartą kulą w $D$ . Wtedy dla każdego $x,y\in K$ ,

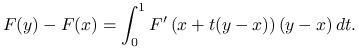$F(y)-F(x)=\int _{0}^{1}F^{{\prime}}\left(x+t(y-x)\right)(y-x)\, dt.$

Dowód

Ustalmy $x,y\in K$ . Ponieważ $K\subset D$ jest wypukły, to $x+t(y-x)$ dla $t\in[0,1]$ i dla $t\in[0,1]$ jest dobrze określona funkcja $g(t)=F(x+t(y-x))$ .

Na mocy założeń standardowych $F^{{\prime}}(\cdot)$ jest ciągła na $\bar{K}$ , zatem także $g^{{\prime}}(t)=F^{{\prime}}(x+t(y-x))(y-x)$ jest ciągła na $[0,1]$ (i całkowalna). Teza lematu wynika więc z podstawowego twierdzenia rachunku różniczkowego, że

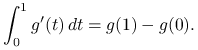$\int _{0}^{1}g^{{\prime}}(t)\, dt=g(1)-g(0).$

∎

Lemat 9.2 (o lokalnym oszacowaniu funkcji i pochodnej)

Przy założeniach standardowych, istnieje dostatecznie małe $\delta>0$ takie, że dla dowolnego $x\in K(x^{*},\delta)$ zachodzi:

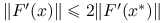$\| F^{{\prime}}(x)\|\leq 2\| F^{{\prime}}(x^{*})\|$ ,
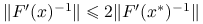$\| F^{{\prime}}(x)^{{-1}}\|\leq 2\| F^{{\prime}}(x^{*})^{{-1}}\|$ ,
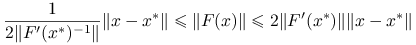$\dfrac{1}{2\| F^{{\prime}}(x^{*})^{{-1}}\|}\| x-x^{*}\|\leq\| F(x)\|\leq 2\| F^{{\prime}}(x^{*})\|\| x-x^{*}\|$ ,

Ćwiczenie 9.1

Wykaż, że przy założeniach standardowych $x^{*}$ musi być izolowanym rozwiązaniem równania $F(x)=0$ .

Rozwiązanie:

Z lematu 9.2 o oszacowaniu funkcji, istnieje otoczenie $U\ni x^{*}$ takie, że

$\dfrac{1}{2\| F^{{\prime}}(x^{*})^{{-1}}\|}\| x-x^{*}\|\leq\| F(x)\|.$

Jeśli więc dla $\tilde{x}$ leżącego w tym otoczeniu $F(\tilde{x})=0$ , to znaczyłoby to, że $\|\tilde{x}-x^{*}\|\leq 0$ , a więc $\tilde{x}=x^{*}$ . Czyli w $U$ nie ma innych rozwiązań niż $x^{*}$ .

Twierdzenie 9.3 (o zbieżności metody Newtona)

Przy standardowych założeniach, istnieją $C>0$ (dostatecznie duże) i $\delta>0$ (dostatecznie małe) takie, że jeśli $x_{0}\in K(x^{*},\delta)$ , to ciąg $(x_{k})$ zadany metodą Newtona (9.2) jest dobrze określony, $x_{k}\in K(x^{*},\delta)$ , oraz $x_{k}\rightarrow x^{*}$ . Co więcej, ciąg ten jest zbieżny kwadratowo:

$\displaystyle\| x_{{k+1}}-x^{*}\|\leq C\| x_{{k}}-x^{*}\|^{2}\qquad\forall k\in\mathbb{N}.$

(9.3)

Dowód

Dowód będzie opierał się na wykazaniu oszacowania (9.3), pozostałe elementy tezy będą jego konsekwencją.

Na wstępie wybierzmy $\delta$ takie, by zachodził lemat 9.2 o oszacowaniu funkcji i pochodnej. Oznaczając $e_{k}=x_{k}-x^{*}$ mamy ze wzoru Newtona

$e_{{k+1}}=e_{k}-F^{{\prime}}(x_{k})^{{-1}}F(x_{k}).$

Na mocy założeń standardowych i lematu o wartości średniej,

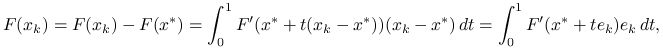$F(x_{k})=F(x_{k})-F(x^{*})=\int _{0}^{1}F^{{\prime}}(x^{*}+t(x_{k}-x^{*}))(x_{k}-x^{*})\, dt=\int _{0}^{1}F^{{\prime}}(x^{*}+te_{k})e_{k}\, dt,$

zatem

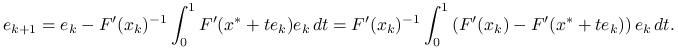$e_{{k+1}}=e_{k}-F^{{\prime}}(x_{k})^{{-1}}\int _{0}^{1}F^{{\prime}}(x^{*}+te_{k})e_{k}\, dt=F^{{\prime}}(x_{k})^{{-1}}\int _{0}^{1}\left(F^{{\prime}}(x_{k})-F^{{\prime}}(x^{*}+te_{k})\right)e_{k}\, dt.$

Korzystając z lipschitzowskości pochodnej i raz jeszcze z lematu 9.2 o oszacowaniu pochodnej, dostajemy

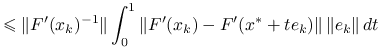	$\displaystyle\\| e_{{k+1}}\\|$	$\displaystyle\leq\\| F^{{\prime}}(x_{k})^{{-1}}\\|\int _{0}^{1}\\| F^{{\prime}}(x_{k})-F^{{\prime}}(x^{*}+te_{k})\\|\,\\| e_{k}\\|\, dt$
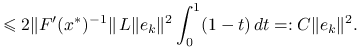		$\displaystyle\leq 2\\| F^{{\prime}}(x^{*})^{{-1}}\\|\, L\\| e_{k}\\|^{2}\int _{0}^{1}(1-t)\, dt=:C\\| e_{k}\\|^{2}.$

Stąd wynika, że jeśli $C\delta<1$ oraz $x_{k}\in K(x^{*},\delta)$ , to także $x_{{k+1}}\in K(x^{*},\delta)$ , a więc ciąg $(x_{k})$ jest dobrze określony. Co więcej, gdy $C\delta<1$ to

$\displaystyle\| e_{{k+1}}\|\leq C\| e_{k}\|^{2}=C\| e_{k}\|\,\| e_{k}\|\leq C\delta\| e_{k}\|,$

a więc ciąg $e_{k}$ jest zbieżny (co najmniej liniowo — a w rzeczywistości co najmniej kwadratowo) do zera.

∎

Ćwiczenie 9.2

Wykaż, że jeśli w założeniach standardowych zastąpić warunek lipschitzowskości pochodnej warunkiem

$\exists\alpha\in(0,1]\;\exists L>0\quad\| F^{{\prime}}(x)-F^{{\prime}}(y)\|\leq L\| x-y\|^{{\alpha}}\qquad\forall x,y\in D,$

(czyli założyć, że $F^{{\prime}}$ jest w swej dziedzinie hölderowska z wykładnikiem $\alpha$ ), to metoda Newtona będzie lokalnie zbieżna z wykładnikiem zbieżności co najmniej $1+\alpha$ .

Wskazówka:

Wystarczy powielić dowód twierdzenia przy standardowych założeniach, modyfikując oszacowanie $\| F^{{\prime}}(x_{k})-F^{{\prime}}(x^{*}+te_{k})\|$ .

Ćwiczenie 9.3

Jak, przy założeniach standardowych, oszacować normę błędu, $\| x_{k}-x^{*}\|$ , przez normę residuum, $\| F(x_{k})\|$ ?

9.3.2. Implementacja metody Newtona

Implementując metodę Newtona, nie będziemy rzecz jasna nigdy explicite wyznaczali macierzy odwrotnej $F^{{\prime}}(x_{k})^{{-1}}$ , tylko rozwiązywali układ równań z macierzą $F^{{\prime}}(x_{k})$ — tę jednak będziemy już musieli wyznaczyć. Pamiętając także o tym, że metoda Newtona jest metodą iteracyjną, stosując ją będziemy musieli zadbać o postawienie sensownego kryterium zatrzymania metody. Odkładając na bok pytanie o konkretny warunek stopu (por. rozdział 7.5), możemy schematycznie zapisać algorytm realizujący metodę Newtona w następujący sposób:

Schemat metody Newtona

function Newton(x, F, stop)

while not stop do begin

oblicz macierz pochodnej $F^{{\prime}}(x)$ ;

rozwiąż $F^{{\prime}}(x)s=F(x)$ ;

x = x - s;

end

return(x);

Ćwiczenie 9.4

Macierzowe zadanie własne dla symetrycznej macierzy $A\in\mathbb{R}^{{N\times N}}$ , znajdowania pary $(x,\lambda)\in\mathbb{R}^{N}\times\mathbb{R}$ spełniającej

$Ax=\lambda x,\qquad x\neq 0$

można potraktować jako kwadratowe równanie nieliniowe dla $F:\mathbb{R}^{{N+1}}\rightarrow\mathbb{R}^{{N+1}}$ danej na przykład wzorem

$F(x,\lambda)=\begin{pmatrix}Ax-\lambda x\\ 1-\frac{1}{2}x^{T}x\end{pmatrix}.$

Zdefiniuj metodę Newtona dla $F$ . Wykaż, że jeśli $\lambda$ jest jednokrotną wartością własną, to metoda Newtona dla $F$ będzie lokalnie zbieżna kwadratowo.

Rozwiązanie:

Mamy

$F^{{\prime}}(x,\lambda)=\begin{pmatrix}A-\lambda I&-x\\ -x^{T}&0\end{pmatrix}.$

Zatem metodę Newtona można — jeśli tylko $F^{{\prime}}(x,\lambda)$ nieosobliwa — zaimplementować, korzystając na przykład ze wzoru Shermana–Morrisona (por. ćwiczenie 5.23).

Zauważmy, że $F$ jest funkcją gładką, jej pochodna jest lipschitzowska ze stałą Lipschitza równą… no właśnie, ile? Mamy

$F^{{\prime}}(x,\lambda)-F^{{\prime}}(y,\mu)=\begin{pmatrix}(\mu-\lambda)I&y-x\\ (y-x)^{T}&0\end{pmatrix},$

zatem

	$\displaystyle\\| F^{{\prime}}(x,\lambda)-F^{{\prime}}(y,\mu)\\| _{1}$	$\displaystyle=\max\{\|\mu-\lambda\|+\|(y-x)_{1}\|,\ldots,\\| y-x\\| _{1}\}$
		$\displaystyle\leq\\| y-x\\| _{1}+\|\mu-\lambda\|=\\|\begin{pmatrix}x\\ \lambda\end{pmatrix}-\begin{pmatrix}y\\ \mu\end{pmatrix}\\| _{1}.$

A więc — w normie indukowanej normą $\|\cdot\| _{1}$ — $F^{{\prime}}$ jest lipschitzowska ze stałą równą 1.

Pozostaje jeszcze sprawdzić, czy w rozwiązaniu — parze własnej $x^{*},\lambda^{*}$ — macierz pochodnej jest nieosobliwa. Ponieważ dla macierzy symetrycznej $A=Q\Lambda Q^{T}$ , gdzie $\Lambda$ jest macierzą diagonalną z wartościami własnymi macierzy $A$ , a kolumny macierzy ortogonalnej $Q$ są wektorami własnymi odpowiadającymi tym wartościom własnym, to

$\begin{pmatrix}Q^{T}&\\ &1\end{pmatrix}F^{{\prime}}(x,\lambda)\begin{pmatrix}Q&\\ &1\end{pmatrix}=\begin{pmatrix}\Lambda-\lambda I&Q^{T}x\\ x^{T}Q&0\end{pmatrix}.$

Niech $\lambda^{*}=\lambda _{i}$ . Wtedy $x^{*}=Cq_{i}$ dla pewnej stałej $C$ . Mamy więc, że $\Lambda-\lambda^{*}I$ jest macierzą diagonalną, która na diagonali ma zero jedynie na $i$ -tej pozycji (na mocy założenia, że $\lambda^{*}$ jest pojedynczą wartością własną) oraz $Q^{T}x=Ce_{i}$ , gdzie $e_{i}$ oznacza $i$ -ty wektor jednostkowy. Nietrudno sprawdzić wprost, że taka macierz jest pełnego rzędu.

Ćwiczenie 9.5 (Metoda Schultza wyznaczania macierzy odwrotnej, [15])

Niech $A$ będzie macierzą nieosobliwą i rozważmy iterację

$X_{{k+1}}=X_{k}+X_{k}(I-AX_{k}),$

startującą z macierzy kwadratowej $X_{0}$ . Wykaż, że jeśli $\| I-AX_{0}\|<1$ , to $X_{k}\rightarrow A^{{-1}}$ gdy $k\rightarrow\infty$ .

Wskazówka:

Wykaż, że $\| I-AX_{{k+1}}\|=\| I-AX_{{k}}\|^{2}$ , a metoda jest w rzeczywistości metodą Newtona zastosowaną do równania macierzowego $F(X)=A-X^{{-1}}=0$ .

Przykład 9.4 (Metoda Newtona dla równania Allena–Cahna)

Przypomnijmy (zob. przykład 9.1), że równanie nieliniowe, które nas interesuje w przypadku stacjonarnym ma postać

$F(U_{N})=P_{N}U_{N}+f(U_{N}),$

a w przypadku ewolucyjnym —

$F(U_{N})=U_{N}+\tau(P_{N}U_{N}+f(U_{N})).$

Oba przypadki możemy zatem ogarnąć, definiując funkcję

$F_{{\tau,\alpha}}(U_{N})=\alpha U_{N}+\tau(P_{N}U_{N}+f(U_{N})),$

która dla $\alpha=1$ i $\tau\ll 1$ daje nam przypadek ewolucyjny, a dla $\alpha=0$ i $\tau=1$ redukuje się do przypadku stacjonarnego równania Allena–Cahna.

Wystarczy więc tylko wyznaczyć pochodną $F_{{\tau,\alpha}}^{{\prime}}(U_{N})$ . Ponieważ (traktując $f$ jako funkcję na $\mathbb{R}^{{N^{2}}}$ )

$f(U_{N})_{{j}}=\delta u_{j}(1-u_{j}^{2})+g_{j},$

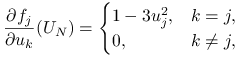$\frac{\partial f_{{j}}}{\partial u_{k}}(U_{N})=\begin{cases}1-3u_{j}^{2},&k=j,\\ 0,&k\neq j,\end{cases}$

zatem ostatecznie

$F_{{\tau,\alpha}}^{{\prime}}(U_{N})\, V=(\alpha I+\tau(P_{N}+\text{diag}(1-3u_{j}^{2})))\, V.$

Przykład 9.5 (Numeryczne eksperymenty z metodą Newtona dla równania Allena–Cahna)

Dla uproszczenia, w eksperymentach numerycznych dotyczących działania różnych metod rozwiązywania równania Allena–Cahna opisywanego w przykładzie 9.1, będziemy rozważać dyskretyzacje jednowymiarowego stacjonarnego równania Allena–Cahna,

$(T_{N}u)_{j}+\delta u_{j}(1-u_{j}^{2})=g_{j},\qquad j=1,\ldots,N,$

gdzie $\delta=10$ oraz $g_{j}=j/(N+1)$ .

%
% rozwiazania zadania z macierza rozrzedzona
% 
disp('Matematyka obliczeniowa II');

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function [x, resid, info, output] = newton(nazwa_f, nazwa_df, x0, atol, rtol, step, maxit)
%
%	[x, resid, info, output] = newton(nazwa_f, x0, atol, rtol, step, maxit)
%
% Rozwiazuje uklad rownan nieliniowych F(x) = 0, gdzie F jest zadana M-funkcja o 
% nazwie ”nazwa_f”.
% Parametry wejscia:
% 	nazwa_f - nazwa M-funkcji zadajacej funkcje F(). 
% 		Ta funkcja *musi* przyjmowac takze argumenty macierzowe!
% 	x0 - przyblizenie poczatkowe rozwiazania
%	atol, rtol - tolerancja bledu residualnego
%	step - co ile iteracji uaktualniac macierz pochodnej; step = 1 daje standardowa metode Newtona, step > maxit daje metode cieciw
%	maxit - maksymalna dopuszczalna liczba iteracji
% Wyjscie:
%	x - koncowe przyblizenie rozwiazania
%	resid - wektor zawierajacy historie zbieznosci, resid(i) - wartosc
% 		normy residuum w i-tej iteracji
%	info - kod zakonczenia: = 1 - sukces, = 0 - przekroczona maxit
%	output - struktura zawierajaca statystyki

% kilka pomocniczych definicji
epsq = sqrt(eps);	% pierwiastek z podwojonej precyzji maszyny
unit = ones(size(x0));	% wektor zlozony z samych jedynek

% poczatkowe rozwiazanie przyblizone
x = x0;
	
% wyznaczenie residuum poczatkowego
fx = feval(nazwa_f, x);
iter = 1;
resid(iter) = norm(fx);

while( (resid(iter) >= (atol + rtol*resid(1))) && (iter < maxit) )

if (mod(iter-1, step) == 0)
		% aproksymacja pochodnej - wszystkie kolumny jednoczesnie
		h = epsq*max(abs(x),unit);
		xh = x*unit' + diag(h);
		if exist(nazwa_df) > 0 
			Df = feval(nazwa_df, x);
		else
			Df = (feval(nazwa_f, xh) - fx*unit')./(unit*h');
		end
		% rozklad macierzy pochodnej do wykorzystania
		[L, U, p] = lu(Df, 'vector');
	end
	% poprawka przyblizonego rozwiazania, x = x - Df\fx;
	x = x - U\(L\fx(p));
	
	% wyznaczenie residuum
	fx = feval(nazwa_f, x);
	iter = iter + 1;
	resid(iter) = norm(fx);
end
info = ~(iter == maxit);
output.iterations = iter - 1;
end

function y = acfun(u) % lewa strona rownania Allena-Cahna
global T; % macierz laplasjanu
global delta;
global x; % wektor wezlow zmiennej przestrzennej
y = T*u + delta*u.*(1-u.^2) - repmat(delta*sqrt(x),[1, size(u,2)]);
end

function y = acdfun(u) % pochodna acfun
global T; % macierz laplasjanu
global delta;
y = T + delta*spdiag(1-3*u.^2);
end

global T;
global delta;
global x;

atol = 1e-8; rtol = 0; maxit = 300; delta = 10;
Nrange = [25, 250]; % zestaw wartosci testowych parametru p
for k = 1:length(Nrange)
	N = Nrange(k); % rozmiar macierzy
	x = linspace(0,1,N+2)'; x = x(2:end-1);
	e = ((N+1)^2)*ones(N,1); T = spdiags([-e, 2*e, -e], [-1,0,1], N,N);
	u0 = ones(N,1);

tic; [u, resid, info, output] = newton('acfun', 'acdfun', u0, atol, rtol, 1, maxit);
	time(k) = toc;

opts.TolFun = atol;
	opts.MaxIter = maxit;
	tic; [U, fU, Info, Output] = fsolve('acfun',u0, opts); timeg(k) = toc;  
	
	% rozwiazanie
	plot(x,[u,U], ['b-;u_{Newton};';'r-;u_{fsolve};']); pause(1);
	
	% residuum
	semilogy(x,abs([acfun(u),acfun(U)]), ['b-;|F(u_{Newton})|;';'r-;|F(u_{fsolve})|;']); pause(1);
	
	% historia zbieznosci metody Newtona
	semilogy(resid,'b-o;|F(u_{Newton})|;'); pause(1);
	
	[norm(acfun(u)),norm(acfun(U))]
end

Ćwiczenie 9.6

Przeprowadź podobne eksperymenty numeryczne dla równania Allena–Cahna w kwadracie, jak to opisywano we wcześniejszych przykładach.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.