Zagadnienia

Podstawowa literatura

Wprowadzenie

Przedmiotem naszego zainteresowania będą metody rozwiązywania czterech podstawowych zadań obliczeniowych, bardzo często spotykanych w rozmaitych działach matematyki stosowanej:

Układ równań liniowych

Dla danej macierzy rzeczywistej 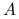$A$ rozmiaru 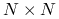$N\times N$ i wektora 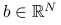$b\in\mathbb{R}^{N}$ znaleźć 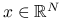$x\in\mathbb{R}^{N}$ taki, że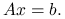

$Ax=b.$

Układ równań nieliniowych

Dla danej funkcji 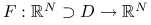$F:\mathbb{R}^{N}\supset D\rightarrow\mathbb{R}^{N}$ i wektora 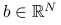$b\in\mathbb{R}^{N}$ znaleźć 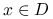$x\in D$ taki, że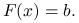

$F(x)=b.$

Zagadnienie własne

Dla danej macierzy rzeczywistej 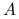$A$ rozmiaru 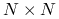$N\times N$ znaleźć 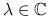$\lambda\in\mathbb{C}$ i niezerowy wektor 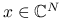$x\in\mathbb{C}^{N}$ takie, że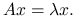

$Ax=\lambda x.$

Całkowanie

Mając daną 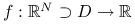$f:\mathbb{R}^{N}\supset D\rightarrow\mathbb{R}$ , obliczyć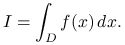

$I=\int _{D}f(x)\, dx.$

Bez wielkiej przesady można powiedzieć, że w każdej poważniejszej symulacji wykonywanej na użytek inżynierski, bankowy, naukowy, itp., któreś (lub kilka) z powyższych zadań występuje jako jądro obliczeniowe, nierzadko o krytycznym znaczeniu. Dlatego jest tak ważne, by potrafić takie zadania rozwiązywać szybko i dokładnie.

Wymienione zadania mają w zastosowaniach jeszcze jedną wspólną cechę: jest nią duży (lub bardzo duży) rozmiar zadania $N$ . Przykładowo, układy równań liniowych spotykane w symulacjach układów elektronicznych mogą mieć kilka milionów niewiadomych. W finansach konieczne jest obliczanie całek z bardzo skomplikowanych funkcji, po kostce 360-wymiarowej. Algorytm stosowany w wyszukiwarce Google musi wyznaczyć wektor własny odpowiadający dominującej wartości własnej macierzy o miliardowym rozmiarze. Dyskretyzacje nieliniowych układów równań różniczkowych (na przykład, równania Naviera–Stokesa), bardzo szybko mogą doprowadzić do nieliniowych układów równań o milionie niewiadomych, a ludzie prowadzący symulacje turbulentnego przepływu cieczy z radością uścisnęliby nas, gdybyśmy tylko dali im szansę wykonana obliczeń z $10^{{12}}$ (lub więcej!) niewiadomych.

Zadania obliczeniowe o tak wielkim rozmiarze wymagają specjalnych algorytmów numerycznych. Przykładowo, naiwnie obliczając całkę

$\int _{{[0,1]^{N}}}f(x_{1},\ldots,x_{N})\, dx_{1}\ldots dx_{N}$

jako całkę iterowaną

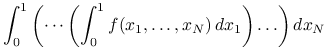$\int _{0}^{1}\left(\cdots\left(\int _{0}^{1}f(x_{1},\ldots,x_{N})\, dx_{1}\right)\ldots\right)dx_{N}$

i stosując do wyznaczenia każdej z całek jednowymiarowych na przykład złożoną kwadraturę trapezów opartą na $n\geq 2$ węzłach, musielibyśmy obliczyć aż $n^{N}$ samych tylko wartości funkcji! (Gdy $N=360$ , jak w finansach, a za $n$ weźmiemy skromnie $n=10$ , należałoby wyznaczyć $10^{{360}}$ samych tylko wartości funkcji — co nie rokuje zbyt dobrze, zważywszy, że współczesne komputery osobiste w ciągu jednego roku mogą w najlepszym razie wykonać ,,zaledwie” $10^{{15}}$ operacji arytmetycznych, a najszybsze na świecie superkomputery mogą teoretycznie wykonać $10^{{20}}$ takich operacji rocznie…)

W naszych rozważaniach o sposobach rozwiązywania Wielkiej Czwórki Zadań będziemy stąpać po solidnym gruncie, omawiając metody klasyczne: sprawdzone w praktyce i teoretycznie dobrze zbadane. Co ciekawe, do ich zrozumienia i analizy będzie nam potrzebna jedynie podstawowa wiedza z Analizy i GALu, a także nieco elementarnych wiadomości z Rachunku Prawdopodobieństwa. W wykładzie bardzo mało będziemy odwoływać się wprost do materiału z Matematyki Obliczeniowej I: jego treść jest w znacznej mierze ortogonalna do tego przedmiotu — ale oczywiście pewna wiedza o metodach numerycznych może nam pomóc lepiej umieścić omawiane kwestie na tle szerszego spektrum zagadnień matematyki obliczeniowej.

Wraz z możliwościami obliczeniowymi komputerów rosną także nasze potrzeby i wymagania, a zjawiska, jakie chcemy symulować numerycznie stają się coraz bardziej złożone, wykraczając poza podstawowe zadania omawiane w skrypcie. Mamy nadzieję, że zdobyta na niniejszym wykładzie wiedza i doświadczenie pozwolą Państwu świadomie korzystać z gotowych pakietów obliczeniowych (więcej na ten temat w wykładzie z Obliczeń naukowych) i w przyszłości zmierzyć się także z nowymi, trudniejszymi wyzwaniami.

Podstawowa literatura

W części dotyczącej metod iteracyjnych dla układów równań liniowych oparliśmy się głównie na podręcznikach [13] oraz [9]. Metody iteracyjne dla układów równań nieliniowych omówiono wzorując się na [9].

Niektóre z poruszanych tu zagadnień są w ciekawy i nieco odmienny od tu zaprezentowanego sposób przedstawione w [4].

Rozdziały 1—4 oraz 13—15 napisał Leszek Plaskota, a autorem rozdziałów 5—12 jest Piotr Krzyżanowski. Dziękujemy Leszkowi Marcinkowskiemu, który prowadził wykład z tego przedmiotu, za wskazanie usterek obecnych we wcześniejszych wersjach skryptu.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Matematyka obliczeniowa II

Zagadnienia

Wprowadzenie

Podstawowa literatura