Zagadnienia

16.1 Przestrzenie Sobolewa $H^{m}$
16.2 Zgodna metoda elementu skończonego
- 16.2.1 Element skończony - ujęcie formalne
16.3 Elementy aproksymacji w przestrzeniach Sobolewa $H^{k}$

16. Przestrzenie elementu skończonego, a aproksymacja w przestrzeniach Sobolewa

W tym rozdziale przedstawimy elementy teorii przestrzeni Sobolewa oraz kilka technicznych lematów potrzebnych do dowodów zbieżności metody elementu skończonego. Mimo, że przedstawimy tylko najmniej techniczne dowody odpowiednich lematów to, aby w pełni zrozumieć dowody, należałoby zapoznać się wcześniej z teorią przestrzeni Sobolewa, zob. np. [21].

Materiał w poniższym rozdziale wykracza poza materiał z wykładu.

16.1. Przestrzenie Sobolewa 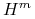$H^{m}$

Poniżej podamy kilka faktów, dotyczących przestrzeni Sobolewa, potrzebnych do udowodnienia zbieżności metody elementu skończonego dla równania eliptycznego drugiego stopnia.

Najpierw zdefiniujmy przestrzenie Sobolewa $H^{k}(\Omega)$ dla $\Omega\subset\mathbb{R}^{d}$ , por. [21].

Definicja 16.1

Rozpatrzmy $\Omega\subset\mathrm{R}^{d}$ obszar ograniczony, wtedy $H^{m}(\Omega)$ definiujemy jako przestrzeń funkcji z $L^{2}(\Omega)$ , których słabe pochodne $\partial^{\alpha}u$ dla wszystkich $|\alpha|\leq m$ są w $L^{2}(\Omega)$ . Iloczyn skalarny w $H^{m}$ definiujemy jako

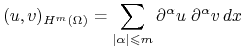$(u,v)_{{H^{m}(\Omega)}}=\sum _{{|\alpha|\leq m}}\partial^{\alpha}u\;\partial^{\alpha}v\, dx$

z normą

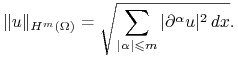$\| u\| _{{H^{m}(\Omega)}}=\sqrt{\sum _{{|\alpha|\leq m}}|\partial^{\alpha}u|^{2}\, dx}.$

i półnormą

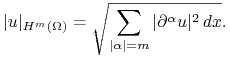$|u|_{{H^{m}(\Omega)}}=\sqrt{\sum _{{|\alpha|=m}}|\partial^{\alpha}u|^{2}\, dx}.$

Tutaj $\alpha=(\alpha _{1},\ldots,\alpha _{d})$ z $\alpha _{j}\in\mathbb{N}$ - to wielowskaźnik, $|\alpha|=\sum _{{k=1}}^{d}\alpha _{k}$ i

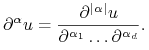$\partial^{\alpha}u=\frac{\partial^{{|\alpha|}}u}{\partial^{{\alpha _{1}}}\ldots\partial^{{\alpha _{d}}}}.$

Można pokazać następujące twierdzenie:

Twierdzenie 16.1

Rozpatrzmy $\Omega\subset\mathbb{R}^{d}$ otwarty obszar z kawałkami gładkim brzegiem i $m\geq 0$ . Wtedy $C^{\infty}(\Omega)\cap H^{m}(\Omega)$ jest zbiorem gęstym w $H^{m}(\Omega)$ .

Proszę zauważyć, że to twierdzenie pozwala nam inaczej zdefiniować przestrzeń $H^{m}$ jako domknięcie zbioru wszystkich funkcji gładkich, których norma $\|\cdot\| _{{H^{m}(\Omega)}}$ jest ograniczona.

Dodatkowo wprowadzamy:

Definicja 16.2

Niech $H^{m}_{0}(\Omega)$ będzie domknięciem w $H^{m}$ przestrzeni $C^{\infty}_{0}$ , gdzie $C^{\infty}_{0}(\Omega)$ jest podprzestrzenią $C^{\infty}(\Omega)$ złożoną z funkcji o zwartym nośniku w $\Omega$ .

Zaznaczmy, że:

$H^{m}_{0}(\Omega)\subset H^{m}(\Omega)\subset L^{2}(\Omega).$

Zachodzą jeszcze następujące nierówności:

Stwierdzenie 16.1 (nierówność Friedrichsa)

Jeśli $\Omega$ zawarty jest w jednostkowej kostce, to

$\| u\| _{{L^{2}(\Omega)}}\leq|u|_{{H^{1}(\Omega)}}\qquad\forall u\in H^{1}_{0}(\Omega).$

Dowód w ogólności można znaleźć np. w [2], ale dla kostek w dwóch i trzech wymiarach dowód pozostawiamy jako zadanie.

Istnieje też następujące twierdzenie mówiące w jakim sensie możemy rozważać wartości funkcji z $H^{1}(\Omega)$ na brzegu tego obszaru.

Twierdzenie 16.2 (Twierdzenie o śladzie)

Rozpatrzmy $\Omega$ ograniczony obszar o brzegu Lipschizowskim¹Brzeg $\Omega$ jest Lipschitzowski (odpowiedniej gładkości), jeśli dla każdego punktu $x\in\partial\Omega$ istnieje otoczenie $\partial\Omega$ tego punktu, które może być reprezentowane jako wykres funkcji Lipschitzowkiej (odpowiednio gładkiej)., wtedy istnieje ograniczony operator liniowy $\gamma:H^{1}(\Omega)\rightarrow L^{2}(\partial\Omega)$ i stała $C$ :

$\|\gamma u\| _{{L^{2}(\partial\Omega)}}\leq C\| u\| _{{H^{1}(\Omega)}}.\qquad\forall u\in H^{1}(\Omega)$

i $\gamma u=u_{{|\partial\Omega}}$ dla wszystkich $u\in C(\overline{\Omega})\cap H^{1}(\Omega)$ .

Funkcję $\gamma u$ nazywamy śladem $u$ na brzegu $\partial\Omega$ .

Kolejnym ważnym twierdzeniem jest tzw. twierdzenie Sobolewa o włożeniu. Tutaj przedstawimy tylko szczególny przypadek potrzebny w przedstawionych dowodach.

Twierdzenie 16.3 (Twierdzenie Sobolewa o włożeniu (ang. Sobolev embedding theorem))

Rozpatrzmy $\Omega$ ograniczony obszar o brzegu Lipschizowskim w $\mathbb{R}^{d}$ dla $d=1,2,3$ , wtedy - jeśli $2*k>d$ - istnieje ciągłe włożenie $H^{2}(\Omega)$ w przestrzeń $C(\overline{\Omega})$ tzn.

	$\displaystyle H^{2}(\Omega)$	$\displaystyle\subset$	$\displaystyle C(\overline{\Omega}),$
	$\displaystyle\exists\, C>0\quad\forall u\in H^{k}(\Omega)\qquad\\| u\\| _{{C(\overline{\Omega})}}$	$\displaystyle\leq$	$\displaystyle C\\| u\\| _{{H^{k}(\Omega)}}.$

Stała $C>0$ zależy od obszaru $\Omega$ .

16.2. Zgodna metoda elementu skończonego

W tym rozdziale przedstawimy ogólne zasady konstrukcji zgodnej metody elementu skończonego. Zgodna metoda oznacza, że przestrzenie elementu skończonego $V^{h}$ zawarte są w przestrzeni wyjściowej $V$ ; w tym przypadku w odpowiedniej przestrzeni Sobolewa.

16.2.1. Element skończony - ujęcie formalne

Najpierw wprowadzimy definicję elementu skończonego za [7], por. także [4] i [2].

Definicja 16.3

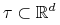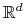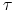Dla $\tau\subset\mathbb{R}^{d}$ wielościanu w $\mathbb{R}^{d}$ . (Części brzegu $\tau$ leżą na hiperpłaszczyznach i są nazywane ścianami)
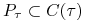$P_{\tau}\subset C(\tau)$ jest przestrzenią funkcji wymiaru 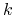$k$ określonych na 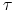$\tau$ (przestrzeń tzw. funkcji kształtu) (ang. shape functions)
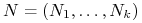$N=(N_{1},\ldots,N_{k})$ jest baza 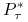$P_{\tau}^{*}$ przestrzeni dualnej do 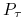$P_{\tau}$ . (Zbiór stopni swobody elementu). Zazwyczaj te funkcjonały wymagają obliczenia wartości funkcji lub jej pochodnych w punktach, dlatego nazywamy je uogólnionymi warunkami interpolacyjnymi.

wtedy elementem skończonym nazywamy trójkę $(\tau,P_{\tau},N)$ .

Definicja 16.4

Dla elementu skończonego $(\tau,P_{\tau},N)$ bazą nodalną tego elementu nazywamy bazę sprzężoną w $P_{\tau}$ do bazy $N$ , tzn. taki układ funkcji z $P_{\tau}$ : $(\phi _{1},\ldots,\phi _{k})$ , że $N_{j}(\phi _{j})=1$ i $N_{j}(\phi _{l})=0$ dla $l\not=j$ .

Jeśli założymy, że funkcjonały z $N$ są określone i ograniczone na większej lub innej przestrzeni liniowej $V$ , to definiujemy:

Definicja 16.5

Dla elementu skończonego $(\tau,P_{\tau},N)$ definiujemy operator interpolacji $\pi _{\tau}:V+P_{\tau}\rightarrow P_{\tau}$ :

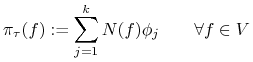$\pi _{\tau}(f):=\sum _{{j=1}}^{k}N(f)\phi _{j}\qquad\forall f\in V$

dla $(\phi _{j})_{{j=0}}^{k}$ bazy nodalnej tego elementu.

Jeśli rozpatrujemy podział obszaru na elementy (triangulacje) i każdy element $\tau$ jest elementem skończonym, tzn. rozpatrujemy trójkę $(\tau,P_{\tau},N_{\tau})$ , to możemy zdefiniować przestrzeń dyskretną dla danego podziału - zwaną dalej przestrzenią elementu skończonego.

Definicja 16.6

Przestrzenią elementu skończonego $V^{h}$ dla triangulacji $T_{h}(\Omega)$ nazywamy dowolną przestrzeń funkcji określonych na $\Omega$ takich, że dla funkcji $u\in V^{h}$ obciętej do elementu $\tau\in T_{h}$ zachodzi własność

$u_{{|\tau}}\in P_{\tau}.$

Oczywiście w praktyce elementy skończone są tego samego typu. Często dokładamy na przestrzenie elementu skończonego warunki ciągłości lub dodatkowe warunki na brzegu obszaru.

Definicja 16.3 elementu skończonego dotyczy pojedynczego elementu, a analiza metody elementu skończonego będzie polegała na tym, że wyniki otrzymane na elemencie wzorcowym przenoszą się na dowolny element, o ile wszystkie elementy są skonstruowane przy pomocy przekształceń afinicznych.

Definicja 16.7

Rodzina przestrzeni elementu skończonego $V^{h}$ dla rodziny triangulacji $T_{h}(\Omega)$ z $\Omega\subset\mathbb{R}^{d}$ jest rodziną afiniczną pod warunkiem, że istnieje element skończony $(\hat{\tau},\hat{P},\hat{N})$ - zwany dalej elementem wzorcowym, i spełnione są następujące warunki: dla dowolnego $\tau _{j}\in T_{h}$ , istnieje przekształcenie afiniczne $F_{j}:\hat{\tau}\rightarrow\tau$ takie, że dla dowolnej funkcji $u\in V^{h}$ istnieje $p\in\hat{P}$ takie, że

$u(x)=p(F_{j}^{{-1}}x)$

oraz dla dowolnego $N_{j}\in N$ istnieje $\hat{N}_{j}\in\hat{N}$ takie, że

$N_{j}(u)=\hat{N}_{j}(u\circ F_{j}).$

Widzimy, że przekształcenie afiniczne spełnia:

$F_{j}\hat{x}=A_{j}\hat{x}+y_{j}\quad\hat{x}\in\hat{\tau},$

dla $A_{j}$ macierzy nieosobliwej $d\times d$ i $y_{j}$ ustalonego wektora.

Stwierdzenie 16.2

Rozpatrzmy afiniczną rodzinę przestrzeni elementu skończonego $\{ V^{h}\}$ dla triangulacji $\{ T_{h}\}$ . Wtedy istnieją takie stałe $C_{1},C_{2}$ , że dla elementu triangulacji $\tau _{j}\in T_{h}$ i dowolnej funkcji $v\in H^{m}(\tau _{j})$ otrzymujemy:

	$\displaystyle\|\hat{v}\|_{{H^{m}(\hat{\tau})}}\leq C_{1}\\| A_{j}\\|^{m}\|det(A_{j})\|^{{-1/2}}\|v\|_{{H^{m}(\tau _{j})}},$
	$\displaystyle\|v\|_{{H^{m}(\tau _{j})}}\leq C_{2}\\| A_{j}^{{-1}}\\|^{m}\|det(A_{j})\|^{{1/2}}\|\hat{v}\|_{{H^{m}(\hat{\tau})}},$

gdzie $\hat{v}(\hat{x})=v(F_{j}\hat{x})$ dla $\hat{x}\in\hat{\tau}$ .

Z gęstości funkcji gładkich w $H^{m}$ możemy założyć, że $v\in C^{\infty}(\overline{\tau})$ . Dowód następnie wynika ze wzoru na różniczkowanie funkcji złożonych:

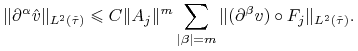$\|\partial^{\alpha}\hat{v}\| _{{L^{2}(\hat{\tau})}}\leq C\| A_{j}\|^{m}\sum _{{|\beta|=m}}\|(\partial^{\beta}v)\circ F_{j}\| _{{L^{2}(\hat{\tau})}}.$

dla $|\alpha|=m$ . Z twierdzenia o podstawianiu otrzymujemy:

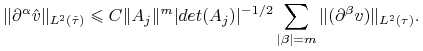$\|\partial^{\alpha}\hat{v}\| _{{L^{2}(\hat{\tau})}}\leq C\| A_{j}\|^{m}|det(A_{j})|^{{-1/2}}\sum _{{|\beta|=m}}\|(\partial^{\beta}v)\| _{{L^{2}(\tau)}}.$

Sumowanie po wszystkich multiindeksach $\alpha$ o długości $m$ kończy dowód.

∎

Stwierdzenie 16.3

Rozpatrzmy afiniczną rodzinę przestrzeni elementu skończonego $\{ V^{h}\}$ dla triangulacji $\{ T_{h}\}$ . Wtedy dla $\tau _{j}\in T_{h}$ zachodzi:

$\displaystyle\| A_{j}\|\leq\frac{\mathrm{diam}(\tau _{j})}{\hat{\rho}},\qquad\| A_{j}^{{-1}}\|\leq\frac{\mathrm{diam}(\hat{\tau})}{\rho _{{\tau _{j}}}},$

gdzie $\hat{\rho}$ jest średnicą okręgu wpisanego we wzorcowy element $\hat{\tau}$ , a $\rho _{{\tau _{j}}}$ jest średnicą okręgu wpisanego w element $\tau _{j}$ .

Widzimy, że

$\| A_{j}\|=\sup _{{\| z\|=1}}\| A_{j}z\|=\hat{\rho}^{{-1}}\sup _{{\| z\|=\hat{\rho}}}\| A_{j}z\|.$

Dla dowolnego $z$ o normie $\hat{\rho}$ istnieją $\hat{x},\hat{y}\in\overline{\hat{\tau}}$ , takie, że $z=\hat{x}-\hat{y}$ . Zatem biorąc $x=F_{j}\hat{x},y=F_{j}\hat{y}\in\overline{\tau _{j}}$ otrzymujemy $x-y=F_{j}(\hat{x})-F_{j}(\hat{y})=A_{j}(\hat{x}-\hat{y})=A_{j}z$ , a stąd

$\| A_{j}\|\leq\hat{\rho}^{{-1}}\| x-y\|\leq\frac{\mathrm{diam}(\tau _{j})}{\hat{\rho}}.$

Drugą nierówność dowodzimy analogicznie.

∎

Jako wniosek otrzymujemy:

Wniosek 16.1

Rozpatrzmy regularną rodzinę triangulacji $\{ T_{h}\}$ ze względu na kształt i afiniczną rodzinę przestrzeni elementu skończonego $\{ V^{h}\}$ dla tych triangulacji. Wtedy istnieją takie stałe $C_{1},C_{2}$ , że dla elementu $\tau _{j}\in T_{h}$ i dowolnej funkcji $v\in H^{m}(\tau _{j})$ zachodzi

	$\displaystyle\|\hat{v}\|_{{H^{m}(\hat{\tau})}}\leq C(\mathrm{diam}(\tau _{j}))^{m}\|det(A_{j})\|^{{-1/2}}\|v\|_{{H^{m}(\tau _{j})}},$
	$\displaystyle\|v\|_{{H^{m}(\tau _{j})}}\leq C\rho _{{\tau _{j}}}^{{-1}}\|det(A_{j})\|^{{1/2}}\|\hat{v}\|_{{H^{m}(\hat{\tau})}},$

gdzie $\hat{v}(\hat{x})=v(F_{j}\hat{x})$ dla $\hat{x}\in\hat{\tau}$ .

16.3. Elementy aproksymacji w przestrzeniach Sobolewa $H^{k}$

Kolejne twierdzenie pozwala oszacować normę $H^{m}$ przez półnormę:

Twierdzenie 16.4 (Lemat Deny-Lionsa)

Niech $\tau\subset\mathbb{R}^{d}$ będzie elementem triangulacji i $l\geq 0$ . Wtedy istnieje stała $C=C(l,d,\tau)$ taka, że

$\inf _{{p\in P_{l}}}\| v+p\| _{{H^{{l+1}}(\tau)}}\leq C|v|_{{H^{{l+1}}(\tau)}}.$

Dowód korzysta z tak zwanej metody zwartości. Można go znaleźć np. w [7], lub [26].

Twierdzenie 16.5

Rozpatrzmy regularną rodzinę triangulacji $\{ T_{h}\}$ ze względu na kształt i afiniczną rodzinę przestrzeni elementu skończonego $\{ V^{h}\}$ dla tych triangulacji. Jeśli warunki interpolacyjne dla elementu wzorcowego $\hat{N}$ są funkcjonałami liniowymi ograniczonymi na przestrzeni $H^{{l+1}}(\hat{\tau})$ oraz $P_{l}\subset\hat{P}\subset H^{{l+1}}(\hat{\tau})$ dla $0\leq l$ , to operator interpolacji nodalnej $\pi _{{\tau _{j}}}$ (por. definicję 16.5) jest poprawnie zdefiniowany oraz dla $0\leq m\leq l+1$ zachodzi:

$|u-\pi _{{\tau _{j}}}u|_{{H^{m}(\tau _{j})}}\leq Ch_{{\tau _{j}}}^{{l+1-m}}|u|_{{H^{{l+1}}(\tau _{j})}}\qquad\forall u\in H^{{l+1}}(\tau _{j}),$

dla $h_{{\tau _{j}}}=\mathrm{diam}(\tau _{j})$ i $C$ zależy od $m,l$ oraz elementu skończonego wzorcowego, i stałej w założeniu regularności ze względu na kształt.

Zauważmy, że $\hat{w}(\hat{x})=w(F_{j}\hat{x})=\pi _{{\hat{\tau}}}\hat{u}(\hat{x})$ dla $\hat{x}\in\hat{\tau}$ i $w=\pi _{{\tau _{j}}}u$ , co wynika z afiniczności rodziny przestrzeni $V^{h}$ (por. definicję 16.7).

Stąd na mocy wniosku 16.1 otrzymujemy, że

$\displaystyle|u-\pi _{\tau}u|_{{H^{m}(\tau)}}=\rho _{{\tau _{j}}}^{{-m}}|det(A_{j})|^{{1/2}}|\hat{u}-\pi _{{\hat{\tau}}}\hat{u}|_{{H^{m}(\hat{\tau})}}\leq C\rho _{{\tau _{j}}}^{{-m}}|det(A_{j})|^{{1/2}}(|\hat{u}|_{{H^{m}(\hat{\tau})}}+|\pi _{{\hat{\tau}}}\hat{u}|_{{H^{m}(\hat{\tau})}}).$

Z założeń twierdzenia otrzymujemy teraz:

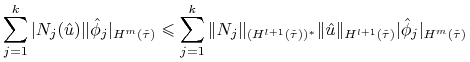	$\displaystyle\|\pi _{{\hat{\tau}}}\hat{u}\|_{{H^{m}(\hat{\tau})}}$	$\displaystyle\leq$	$\displaystyle\sum _{{j=1}}^{k}\|N_{j}(\hat{u})\|\|\hat{\phi}_{j}\|_{{H^{m}(\hat{\tau})}}\leq\sum _{{j=1}}^{k}\\| N_{j}\\| _{{(H^{{l+1}}(\hat{\tau}))^{*}}}\\|\hat{u}\\| _{{H^{{l+1}}(\hat{\tau})}}\|\hat{\phi}_{j}\|_{{H^{m}(\hat{\tau})}}$
		$\displaystyle\leq$	$\displaystyle C\\|\hat{u}\\| _{{H^{{l+1}}(\hat{\tau})}}$

Oczywiście $\pi _{{\hat{\tau}}}p=p$ dla dowolnego $p\in\hat{P}$ , w szczególności dla $p$ wielomianu z $P_{l}$ .

Zatem

$\displaystyle|u-\pi _{\tau}u|_{{H^{m}(\tau)}}\leq C\rho _{{\tau _{j}}}^{{-m}}|det(A_{j})|^{{1/2}}\|\hat{u}+p\| _{{H^{{l+1}}(\hat{\tau})}}\qquad\forall p\in P_{l}.$

Stąd na mocy twierdzenia 16.4 otrzymujemy

$\displaystyle|u-\pi _{\tau}u|_{{H^{m}(\tau)}}$

$\displaystyle\leq$

$\displaystyle C\rho _{{\tau _{j}}}^{{-m}}|det(A_{j})|^{{1/2}}|\hat{u}|_{{H^{{l+1}}(\hat{\tau})}}.$

Z kolei z wniosku 16.1 otrzymujemy