Zagadnienia
10. Metoda różnic skończonych - stabilność schematów dla zadań eliptycznych w normach energetycznych
Materiał w poniższym rozdziale jest materiałem dodatkowym, tzn. nie wchodzi w zakres materiału przedstawianego na wykładzie.
10.1. Wprowadzenie - stabilność dla modelowego zadania
W tym rozdziale przedstawimy krótki zarys innej metody badania stabilności zadań przybliżonych
otrzymanych za pomocą metody różnic skończonych, tym razem, w dyskretnej normie ![]() .
Jest to metoda analogiczna do metody badania stabilności zadań różniczkowych
w równaniach fizyki matematycznej, por. [11].
.
Jest to metoda analogiczna do metody badania stabilności zadań różniczkowych
w równaniach fizyki matematycznej, por. [11].
Przedstawimy tę metodę teraz dla naszej modelowej dyskretyzacji (7.5) z jednorodnymi warunkami brzegowymi:
| (10.1) | |||||
W przypadku niejednorodnych warunków brzegowych dla ![]() , zamiana zmiennych:
, zamiana zmiennych:
![]() dla
dla ![]() rozwiązania zadania z zerowymi warunkami brzegowymi daje
rozwiązania zadania z zerowymi warunkami brzegowymi daje ![]() - rozwiązanie (7.5).
- rozwiązanie (7.5).
Proszę zauważyć, że dla tego zadania dyskretnego zachodzi też stabilność w dyskretnej normie maksimum, por. rozdział 9.
Przyjmujemy oznaczenie ![]() .
Wprowadzamy do przestrzeni
.
Wprowadzamy do przestrzeni ![]() wszystkich funkcji określonych na siatce
wszystkich funkcji określonych na siatce ![]() następujący iloczyn skalarny:
następujący iloczyn skalarny:
![[u,v]_{h}=h\sum _{{x\in\overline{\Omega}_{h}}}u(x)v(x)=h\sum _{{k=0}}^{N}u_{k}v_{k}](wyklady/nrr/mi/mi1355.png) |
będący dyskretnym odpowiednikiem iloczynu skalarnego typu ![]() .
Tutaj
.
Tutaj ![]() .
Wprowadzamy dodatkowo oznaczenia:
.
Wprowadzamy dodatkowo oznaczenia:
![[u,v)_{h}=h\sum _{{k=0}}^{{N-1}}u_{k}v_{k},\qquad(u,v]_{h}=h\sum _{{k=1}}^{N}u_{k}v_{k},\qquad(u,v)_{h}=h\sum _{{k=1}}^{{N-1}}u_{k}v_{k}.](wyklady/nrr/mi/mi1394.png) |
Potrzebujemy następujących odpowiedników różnicowych wzorów na całkowanie przez części nazywanych: różnicowymi wzorami na sumowanie przez części (ang. finite difference summing by parts formulas):
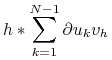 |
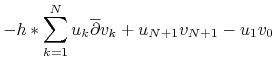 |
|||
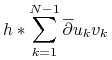 |
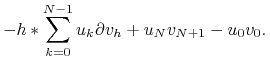 |
Tutaj ![]() i
i
![]() .
Dowód tych wzorów pozostawiamy jako proste zadanie,
por. ćwiczenie 10.1.
Możemy je przedstawić z wykorzystaniem naszej notacji:
.
Dowód tych wzorów pozostawiamy jako proste zadanie,
por. ćwiczenie 10.1.
Możemy je przedstawić z wykorzystaniem naszej notacji:
| (10.2) |
Zauważmy, że ![]() dla
dla ![]() zatem z powyższych wzorów dla
zatem z powyższych wzorów dla ![]() widzimy, że dla
widzimy, że dla ![]() :
:
| (10.3) |
Prawdziwy jest również dyskretny odpowiednik nierówności Friedrichsa:
Twierdzenie 10.1 (różnicowa nierówność Friedrichsa)
Dla ![]() takiej, że
takiej, że ![]() prawdziwa jest nierówność
prawdziwa jest nierówność
Dowód pozostawiamy jako zadanie, por. ćwiczenie 10.1.
Weźmy ![]() dla
dla ![]() rozwiązania (10.1),
przemnóżmy przez
rozwiązania (10.1),
przemnóżmy przez ![]() i zsumujmy po
i zsumujmy po ![]() . Wtedy,
korzystając z wzorów na sumowanie przez części (10.2), otrzymujemy
. Wtedy,
korzystając z wzorów na sumowanie przez części (10.2), otrzymujemy
Możemy skorzystać z różnicowej nierówności Friedrichsa, por. twierdzenie 10.1:
a stąd otrzymujemy oszacowanie:
W przypadku ![]() otrzymujemy oszacowanie bez użycia nierówności Friedrichsa:
otrzymujemy oszacowanie bez użycia nierówności Friedrichsa:
Uzyskaliśmy stabilność w dyskretnej normie ![]() , z której wynika też
istnienie jednoznacznego rozwiązania równego zero dla
, z której wynika też
istnienie jednoznacznego rozwiązania równego zero dla ![]() . Stąd
wynika istnienie jednoznacznego rozwiązania.
. Stąd
wynika istnienie jednoznacznego rozwiązania.
Weźmy ![]() zdefiniowane jako
zdefiniowane jako ![]() dla
dla ![]() .
Takie obcięcie jest zdefiniowane poprawnie dla dowolnej funkcji ciągłej. Zauważmy, że zbiór funkcji ciągłych na
.
Takie obcięcie jest zdefiniowane poprawnie dla dowolnej funkcji ciągłej. Zauważmy, że zbiór funkcji ciągłych na ![]() jest gęsty w
jest gęsty w ![]() . Dodatkowo
. Dodatkowo
dla dowolnej funkcji ciągłej na ![]() oraz jeśli rozwiązanie
(7.5) jest w
oraz jeśli rozwiązanie
(7.5) jest w ![]() , to
, to
Korzystając z twierdzenia 8.1 otrzymujemy:
| (10.4) |
Ten przykład jest prosty, ale w ten sam sposób można badać bardziej skomplikowane schematy różnicowe dla zadań postawionych w obszarach w dwóch czy więcej wymiarach.
10.2. Stabilności w normach energetycznych
Przedstawimy teraz ogólną teorię stabilności w dyskretnych normach energetycznych. Dyskretne normy energetyczne są analogiczne do tzw. norm energetycznych, w których bada się stabilność rozwiązań wyjściowych zadań różniczkowych z wykorzystaniem teorii równań fizyki matematycznej.
Zakładamy, że rozpatrujemy rodzinę skończenie wymiarowych przestrzeni Hilberta ![]() z iloczynem skalarnym
z iloczynem skalarnym ![]() oraz operator
oraz operator ![]() . Interesuje nas
zadanie dyskretne:
. Interesuje nas
zadanie dyskretne:
| (10.5) |
Powiemy, że operator liniowy ![]() jest samosprzężony w
jest samosprzężony w ![]() , jeśli
, jeśli
![]() dla
dla ![]() zdefiniowanego jako
zdefiniowanego jako
Powiemy, że ![]() jest dodatnio określony (nieujemnie określony), jeśli
jest dodatnio określony (nieujemnie określony), jeśli
Nierówność operatorową ![]() (
(![]() ) definiujemy jako
) definiujemy jako ![]() (
(![]() ).
Zauważmy, że jeśli
).
Zauważmy, że jeśli ![]() to
to ![]() jest poprawnie zdefiniowanym iloczynem skalarnym, który nazywamy iloczynem skalarnym energetycznym dla operatora
jest poprawnie zdefiniowanym iloczynem skalarnym, który nazywamy iloczynem skalarnym energetycznym dla operatora ![]() . Oznaczmy
. Oznaczmy ![]() jako normę energetyczną dla
jako normę energetyczną dla ![]() .
Zauważmy, że
.
Zauważmy, że ![]() też jest samosprzężony dodatnio określonym operatorem.
Stabilność w odpowiednich normach dyskretnych typu
też jest samosprzężony dodatnio określonym operatorem.
Stabilność w odpowiednich normach dyskretnych typu ![]() , czy normach energetycznych pozwala nam badać następujące twierdzenie:
, czy normach energetycznych pozwala nam badać następujące twierdzenie:
Twierdzenie 10.2
Niech ![]() będzie liniowym operatorem w przestrzeni Hilberta skończenie wymiarowej
będzie liniowym operatorem w przestrzeni Hilberta skończenie wymiarowej ![]() .
Wtedy, dla
.
Wtedy, dla ![]() rozwiązania (10.5) zachodzi:
rozwiązania (10.5) zachodzi:
-
jeśli
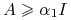 , to
, to
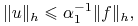
-
jeśli
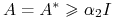 , to
, to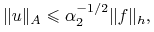
-
jeśli
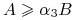 dla
dla 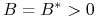 , to
, to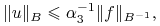
gdzie ![]() dla
dla ![]() są stałymi dodatnimi.
są stałymi dodatnimi.
Dowód pozostawiamy jako zadanie, por. twierdzenia 10.10 w [10].
Przykład 10.1
Zastosujmy powyższe twierdzenia do badania stabilności w przestrzeni Hilberta ![]() funkcji określonych na
funkcji określonych na ![]() dla
dla ![]() z iloczynem skalarnym
z iloczynem skalarnym ![]() dyskretyzacji
(10.1).
Bierzemy, jak powyżej,
dyskretyzacji
(10.1).
Bierzemy, jak powyżej, ![]() dla
dla ![]() przy czym przyjmujemy, że
przy czym przyjmujemy, że ![]() .
.
Pokażemy, że nasz powyższy dowód stabilności bazował na tym, że odpowiedni operator różnicowy jest dodatnio określony w tej przestrzeni.
Definiujemy ![]() jako
jako
Wtedy, przyjmując że ![]() , otrzymujemy jak powyżej (por. wzory na sumowanie przez części (10.2)):
, otrzymujemy jak powyżej (por. wzory na sumowanie przez części (10.2)):
a następnie, z różnicowej nierówności Friedrichsa, por. twierdzenie 10.1, dla ![]() widzimy, że
widzimy, że
czyli ![]() .
A z kolei
.
A z kolei ![]() , czyli jest to operator dodatnio określony i samosprzężony i zachodzi
, czyli jest to operator dodatnio określony i samosprzężony i zachodzi ![]() . Zatem, z pierwszego podpunktu twierdzenia 10.2 otrzymujemy:
. Zatem, z pierwszego podpunktu twierdzenia 10.2 otrzymujemy:
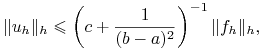 |
a z drugiego i trzeciego - odpowiednio:
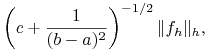 |
||||
Przykład 10.2
Rozpatrzmy następujący problem różniczkowy, powstały z naszego modelowego problemu poprzez dodanie członu z pierwszą pochodną:
dla ![]() stałych, przy czym
stałych, przy czym ![]() .
Dyskretyzujemy ten problem na siatce
.
Dyskretyzujemy ten problem na siatce ![]() dla
dla ![]() dla
dla ![]() w następujący sposób:
w następujący sposób:
| (10.6) | |||||
Tutaj
jest ilorazem różnicowym centralnym. Zauważmy, że ![]() .
Można pokazać, że jeśli rozwiązanie
.
Można pokazać, że jeśli rozwiązanie ![]() , to:
, to:
co pozostawiamy jako zadanie.
Z tego możemy wywnioskować, że rząd aproksymacji wynosi dwa, zarówno w normie dyskretnej maksimum, jak i w ![]() .
.
Weźmy przestrzeń ![]() z tym samym iloczynem skalarnym i operator
z tym samym iloczynem skalarnym i operator ![]() z przykładu 10.1.
z przykładu 10.1.
Wtedy, z wzorów na różnicowe sumowanie przez części (10.2), otrzymujemy:
Stąd ![]() . Zatem, choć
. Zatem, choć ![]() nie jest symetryczny (o ile
nie jest symetryczny (o ile ![]() ),
to jest operatorem dodatnio określonym i zachodzi:
),
to jest operatorem dodatnio określonym i zachodzi:
czyli ![]() .
.
Z powyższego oszacowania możemy pokazać stabilność w normie ![]() jak w przykładzie 10.1, a w konsekwencji zbieżność dyskretną z rzędem dwa, co pozostawiamy jako zadanie.
jak w przykładzie 10.1, a w konsekwencji zbieżność dyskretną z rzędem dwa, co pozostawiamy jako zadanie.
10.3. Zadania
Ćwiczenie 10.1
Udowodnij wzory na sumowanie przez części, tzn. (10.2) oraz różnicową nierówność Friedrichsa, tzn. twierdzenie 10.1.
Ćwiczenie 10.2
Zbadaj rząd i stabilność schematu z przykładu 10.2 dyskretyzacji modelowego problemu jednowymiarowego w ![]() dla
dla ![]() i
i ![]() . Wykaż zbieżności z rzędem dwa w normie
. Wykaż zbieżności z rzędem dwa w normie ![]() , o ile rozwiązanie wyjściowego problemu jest klasy
, o ile rozwiązanie wyjściowego problemu jest klasy ![]() .
.
Ćwiczenie 10.3
Zbadaj stabilność schematu (8.10) dyskretyzacji modelowego problemu dwuwymiarowego
w dyskretnej normie ![]() dla
dla ![]() .
.
Ćwiczenie 10.4
Rozpatrzmy równanie różniczkowe na kwadracie ![]() : chcemy znaleźć
: chcemy znaleźć ![]() :
:
z zerowym warunkiem brzegowym. Tu ![]() są stałymi, a
są stałymi, a ![]() jest dodatkowo nieujemna.
jest dodatkowo nieujemna.
Analogicznie do przykładu 10.2 i dyskretyzacji (8.10), skonstruuj schemat różnicowy wykorzystując odpowiednie pochodne centralne do aproksymacji
pochodnych ![]() .
.
Zbadaj rząd schematu i stabilność w w dyskretnej normie ![]() .
.
Postępuj analogicznie jak w przykładzie 10.2.




