Zagadnienia
6. Sztywność, zmienny krok całkowania i metoda strzałów
W tym rozdziale zajmiemy się ważnymi schematami rozwiązywania tzw. sztywnych układów równań różniczkowych zwyczajnych. Omówimy schematy ze zmiennym krokiem całkowania i metodę strzałów rozwiązywania zadań brzegowych.
6.1. Sztywne równania różniczkowe zwyczajne
Dość trudno jest podać precyzyjnie poprawną matematycznie definicję sztywności dla dowolnego zadania różniczkowego zwyczajnego. My przyjmiemy definicję pragmatyczną za [13]:
Definicja 6.1
Równanie różniczkowe zwyczajne nazywamy sztywnym (ang. stiff), jeśli numeryczne schematy zamknięte, w szczególności metody zamknięte Adamsa, działają zdecydowanie lepiej niż schematy otwarte przybliżonego rozwiązywania zagadnień początkowych.
Oczywiście definicja nie jest do końca precyzyjna. Podamy też inne definicje sztywności (ang. stiffness) np. dla zagadnień liniowych, jakkolwiek powyższa definicja jest dla nas wygodna, ponieważ podkreśla to, że równania sztywne rozwiązujemy przy pomocy schematów zamkniętych. Za chwilę podamy kilka przykładów sztywnych równań różniczkowych, aby przekonać się, że pojawiają się one dość często w realistycznych modelach nauk przyrodniczych, por. rozdział 6.2.
6.1.1. Przypadek skalarny
W rozdziale 3.3.1 już zobaczyliśmy, że dla modelowego zadania skalarnego:
rozwiązanie uzyskane przy pomocy otwartego schematu Eulera zachowuje własności rozwiązania
![]() , tzn. jest dodatnie i malejące do zera dla
, tzn. jest dodatnie i malejące do zera dla ![]() tylko wtedy, gdy jest spełniony warunek:
tylko wtedy, gdy jest spełniony warunek:
![]() W przypadku gdy
W przypadku gdy ![]() jest bardzo duże, warunek ten wymusza, że musimy stosować bardzo małe
jest bardzo duże, warunek ten wymusza, że musimy stosować bardzo małe ![]() .
Natomiast rozwiązanie uzyskane przy pomocy zamkniętego
schematu Eulera zachowuje własności powyższe rozwiązania dla dowolnego
.
Natomiast rozwiązanie uzyskane przy pomocy zamkniętego
schematu Eulera zachowuje własności powyższe rozwiązania dla dowolnego ![]() .
.
Schemat zamknięty Eulera można zatem uznać za lepszy od schematu otwartego dla tego zagadnienia dla ujemnego ![]() o dużym module.
o dużym module.
6.1.2. Przypadek wielowymiarowy
Załóżmy, że rozpatrujemy jednorodne liniowe równanie różniczkowe zwyczajne ze stałymi współczynnikami:
gdzie ![]() - to macierz o stałych współczynnikach taka, że w pewnej bazie jest ona diagonalizowalna, tzn.
istnieje macierz nieosobliwa
- to macierz o stałych współczynnikach taka, że w pewnej bazie jest ona diagonalizowalna, tzn.
istnieje macierz nieosobliwa ![]() taka, że
taka, że
z
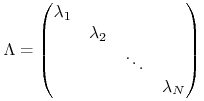 |
Załóżmy, że wszystkie ![]() , wtedy oczywiście rozwiązaniem
jest
, wtedy oczywiście rozwiązaniem
jest
Oznaczmy ![]() -tą kolumnę macierzy
-tą kolumnę macierzy ![]() przez
przez ![]() , tzn.
, tzn.
![]() , wtedy otrzymujemy:
, wtedy otrzymujemy:
dla ![]() .
Jeśli zastosujemy otwarty schemat Eulera do tego zagadnienia,
to analogicznie jak w poprzednim rozdziale otrzymujemy, że
.
Jeśli zastosujemy otwarty schemat Eulera do tego zagadnienia,
to analogicznie jak w poprzednim rozdziale otrzymujemy, że
Czyli: o ile ![]() (
(![]() ) tym odpowiednia składowa rozwiązania
) tym odpowiednia składowa rozwiązania
![]() szybciej dąży do zera. Z drugiej strony warunek na
to, aby odpowiadająca składowa rozwiązania dyskretnego otrzymanego otwartym schematem Eulera nie zmieniała znaku i zbiegała do zera wynosi:
szybciej dąży do zera. Z drugiej strony warunek na
to, aby odpowiadająca składowa rozwiązania dyskretnego otrzymanego otwartym schematem Eulera nie zmieniała znaku i zbiegała do zera wynosi:
czyli jest to warunek ograniczający dopuszczalny zakres wartości ![]() .
.
Widzimy zatem, że otwarty schemat Eulera dla takiego równania jest zupełnie niepraktyczny
na dłuższych odcinkach czasu, ponieważ ograniczenie na ![]() związane jest ze składowymi rozwiązań, które najszybciej zanikają, czyli na dłuższym odcinku czasu nie mają większego wpływu na rozwiązanie.
Z kolei dla schematu zamkniętego Eulera nie otrzymujemy żadnych ograniczeń na
związane jest ze składowymi rozwiązań, które najszybciej zanikają, czyli na dłuższym odcinku czasu nie mają większego wpływu na rozwiązanie.
Z kolei dla schematu zamkniętego Eulera nie otrzymujemy żadnych ograniczeń na ![]() , ponieważ:
, ponieważ:
Widzimy, że dla tego typu równań schemat otwarty zachowuje się gorzej niż odpowiedni schemat zamknięty, co jest zgodne z naszą oryginalną definicją sztywności. W ogólnym przypadku, gdy wszystkie części rzeczywiste wartości własnych macierzy ![]() są ujemne sytuacja jest analogiczna.
są ujemne sytuacja jest analogiczna.
Zatem definiujemy zadanie liniowe jednorodne jako sztywne, jeśli:
-
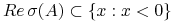
-
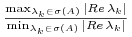 jest duże.
jest duże.
Tutaj ![]() oznacza zbiór wartości własnych macierzy
oznacza zbiór wartości własnych macierzy ![]() .
Oczywiście w tej definicji nie jest doprecyzowane co oznacza <<duże>>, ale łatwo określić, że jeśli stosunek w drugim punkcie jest równy dziesięć, to układ nie jest sztywny, a jeśli
.
Oczywiście w tej definicji nie jest doprecyzowane co oznacza <<duże>>, ale łatwo określić, że jeśli stosunek w drugim punkcie jest równy dziesięć, to układ nie jest sztywny, a jeśli ![]() to układ jest sztywny.
Rozszerza się powyższą definicję sztywności na układy równań nieliniowych przyjmując, że układ:
to układ jest sztywny.
Rozszerza się powyższą definicję sztywności na układy równań nieliniowych przyjmując, że układ:
jest sztywny w obszarze ![]() i dla
i dla ![]() z odcinka
z odcinka ![]() jeśli Jakobian
jeśli Jakobian ![]() , czyli
, czyli ![]() spełnia powyższą definicję dla każdego
spełnia powyższą definicję dla każdego ![]() i
i ![]() .
.
Wadą powyższej definicji sztywności jest to, że nie obejmuje np. układu skalarnego ![]() dla
dla ![]() .
.
6.2. Przykłady schematów sztywnych
W tym rozdziale podamy kilka przykładów równań sztywnych, por. [13].
6.2.1. Oscylator Van der Pola
Równanie Van der Pola opisujące oscylator z nieliniowym tłumieniem:
gdzie ![]() jest parametrem, dla dużego
jest parametrem, dla dużego ![]() np.
np. ![]() powyższe równanie jest sztywne.
powyższe równanie jest sztywne.
6.2.2. Reakcje chemiczne
Rozważmy następujące reakcje chemiczne, które symbolicznie opiszemy następująco:
co prowadzi do następującego układu równań różniczkowych zwyczajnych:
![\begin{array}[]{lccrrrrrr}A:&x_{1}^{{\prime}}&=&-0.04*x_{1}&+&10^{4}x_{2}*x_{3}&&\qquad\ x_{1}(0)=1\\
B:&x_{2}^{{\prime}}&=&0.04*x_{1}&-&10^{4}x_{2}*x_{3}&-3*10^{7}x_{2}^{2}&x_{2}(0)=1\\
C:&x_{3}^{{\prime}}&=&&&&3*10^{7}x_{2}^{2}&x_{3}(0)=1\end{array}](wyklady/nrr/mi/mi692.png) |
Czytelnikowi pozostawiamy sprawdzenie z pomocą octave'a, że np. schematy otwarte nie działają najlepiej dla tego problemu.
6.2.3. Równania paraboliczne
Ten przykład jest szczególnym przypadkiem dyskretyzacji równań, których metody dyskretyzacji omawiane są później dokładniej w rozdziale 14.
Rozpatrzmy równanie paraboliczne:
z warunkami brzegowymi ![]() i początkowym
i początkowym ![]() .
.
Dyskretyzując je względem zmiennej przestrzennej ![]() metodą różnic skończonych, tzn. wprowadzając siatkę
metodą różnic skończonych, tzn. wprowadzając siatkę
![]() dla
dla ![]() z
z ![]() i przybliżając drugą pochodną przez
i przybliżając drugą pochodną przez
otrzymujemy następujący układ równań różniczkowych zwyczajnych:
z ![]() (warunki brzegowe) i warunkiem początkowym
(warunki brzegowe) i warunkiem początkowym
![]() i
i ![]() ,
por. rozdział 14.
,
por. rozdział 14.
Oczekujemy, że ![]() gdzie
gdzie ![]() jest rozwiązaniem wyjściowego problemu.
Nietrudno zauważyć, że powyższy układ równań zwyczajnych można zapisać jako
jest rozwiązaniem wyjściowego problemu.
Nietrudno zauważyć, że powyższy układ równań zwyczajnych można zapisać jako
dla ![]() ,
, ![]() i
i
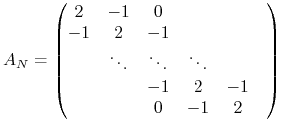 |
(6.1) |
Można pokazać, że wartości własne ![]() są dodatnie i
są dodatnie i
czyli układ jest sztywny dla dużych ![]() , czyli małych
, czyli małych ![]() .
.
Dla przykładowych dużych ![]() możemy sprawdzić, czy rzeczywiście tak jest w octave, że
stosunek największej do najmniejszej wartości własnej wynosi ok.
możemy sprawdzić, czy rzeczywiście tak jest w octave, że
stosunek największej do najmniejszej wartości własnej wynosi ok. ![]() dla
dla ![]() , a dla
, a dla ![]() ten stosunek wynosi ok.
ten stosunek wynosi ok. ![]() .
Tu podajemy kod octave obliczający ten stosunek:
.
Tu podajemy kod octave obliczający ten stosunek:
6.3. Schematy zamknięte. Predyktor-korektor
Schematy zamknięte stosujemy dla zadań sztywnych.
Aby obliczyć kolejne przybliżenie ![]() w schematach zamkniętych, musimy rozwiązać liniowy lub nieliniowy układ równań np.
dla zamkniętego schematu Eulera:
w schematach zamkniętych, musimy rozwiązać liniowy lub nieliniowy układ równań np.
dla zamkniętego schematu Eulera:
czyli w każdym kroku musimy rozwiązać układ równań:
dla funkcji ![]() \textcolor.
\textcolor.
W ogólności dla zamkniętego schematu ![]() -krokowego liniowego musimy w każdym kroku rozwiązać
układ równań względem
-krokowego liniowego musimy w każdym kroku rozwiązać
układ równań względem ![]() :
:
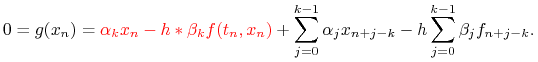 |
Analogiczna sytuację widzimy dla zamkniętych schematów jednokrokowych.
Powyższe równanie (układ równań) możemy rozwiązać przy pomocy różnych metod np. metody Newtona, czy jakiejś wersji
metody iteracji prostej, zob. np. [18], [17].
Zauważmy, że w przypadku otwartego schematu Eulera ![]() jest punktem stałym dla funkcji
jest punktem stałym dla funkcji ![]() , czyli
naturalne jest zastosowanie następującej metody iteracyjnej: dla danego
, czyli
naturalne jest zastosowanie następującej metody iteracyjnej: dla danego ![]() liczymy
liczymy
Z odpowiedniej gładkości pola wektorowego ![]() wynika, że
wynika, że
![]() jest funkcją lipschizowską względem
jest funkcją lipschizowską względem ![]() (lokalnie na
(lokalnie na ![]() ) ze stałą Lipschitza
) ze stałą Lipschitza ![]() i
i ![]() jest ograniczona na kuli
jest ograniczona na kuli ![]() , tzn. dla
, tzn. dla ![]() zachodzi
zachodzi ![]() .
Wtedy
.
Wtedy
i stała Lipschitza ![]() wynosi
wynosi ![]() , ponieważ
, ponieważ
Zatem jeśli dla odpowiednio małego ![]() zachodzi
zachodzi ![]() i
i ![]() , to
, to ![]() jest kontrakcją na
jest kontrakcją na ![]() .
Z tego wynika istnienie
.
Z tego wynika istnienie ![]() i zbieżność metody iteracji prostej.
W przypadku innych schematów zamkniętych
możemy skonstruować analogiczne wersje metody iteracji prostych.
i zbieżność metody iteracji prostej.
W przypadku innych schematów zamkniętych
możemy skonstruować analogiczne wersje metody iteracji prostych.
Postawmy kwestię -
jak dobierać startowe przybliżenie ![]() .
.
Pierwsza opcja to: wziąć ![]() .
Z ciągłości rozwiązania wynika, że jeśli
.
Z ciągłości rozwiązania wynika, że jeśli ![]() jest dostatecznie małe, to
jest dostatecznie małe, to ![]() i
i ![]() są sobie bliskie, a dokładnie zachodzi
są sobie bliskie, a dokładnie zachodzi ![]() .
.
Zastanówmy się, czy można dobrać ![]() lepiej?
lepiej?
Istnieje możliwość, żeby za ![]() brać przybliżenie
brać przybliżenie ![]() obliczone jednym krokiem otwartego schematu
tego samego rzędu
obliczone jednym krokiem otwartego schematu
tego samego rzędu ![]() co schemat zamknięty (oczywiście zbieżnym z tym samym rzędem) tzn.
co schemat zamknięty (oczywiście zbieżnym z tym samym rzędem) tzn.
gdzie ![]() są obliczone wczesniej naszym schematem zamkniętym, a
są obliczone wczesniej naszym schematem zamkniętym, a
![]() jest dowolnym
jest dowolnym ![]() - krokowym otwartym schematem zbieżnym z rzędem
- krokowym otwartym schematem zbieżnym z rzędem ![]() , por. (4.5).
, por. (4.5).
Wtedy widzimy, że ![]() więc i o ile
więc i o ile ![]() dostatecznie małe
dostatecznie małe ![]() .
.
W takim przypadku schemat otwarty nazywamy predyktorem,
a schemat zamknięty, który naprawdę stosujemy do rozwiązania zadania początkowego - korektorem.
Podsumowując;
nazwy schemat predyktor-korektor używa się względem schematu zamkniętego rzędu ![]() , zaimplementowanego w ten sposób, że kolejne
, zaimplementowanego w ten sposób, że kolejne ![]() przybliżenie
przybliżenie ![]() obliczone jest poprzez zastosowanie w każdym kroku czasowym jakiejś metody iteracyjnej rozwiązywania nieliniowego równania (układu równań)
z przybliżeniem
startowym obliczonym odpowiednim pojedyńczym krokiem schematu otwartego tego samego rzędu (predyktorem).
Metoda iteracyjna niekoniecznie musi być taka, jak opisana powyżej.
Do rozwiązywania nieliniowego układu równań można stosować też np. metodę Newtona, czy jeszcze inną metodę iteracyjną, por. np. [18] lub [25].
obliczone jest poprzez zastosowanie w każdym kroku czasowym jakiejś metody iteracyjnej rozwiązywania nieliniowego równania (układu równań)
z przybliżeniem
startowym obliczonym odpowiednim pojedyńczym krokiem schematu otwartego tego samego rzędu (predyktorem).
Metoda iteracyjna niekoniecznie musi być taka, jak opisana powyżej.
Do rozwiązywania nieliniowego układu równań można stosować też np. metodę Newtona, czy jeszcze inną metodę iteracyjną, por. np. [18] lub [25].
W praktyce bierze się odpowiednie pary schematów tego samego rzędu: np. otwarty schemat Eulera za predyktor i zamknięty schemat Eulera za korektor, czy ogólniej - schemat otwarty Adamsa-Bashfordsa rzędu ![]() za predyktor ze schematem zamkniętym Adamsa-Moultona rzędu
za predyktor ze schematem zamkniętym Adamsa-Moultona rzędu ![]() jako korektorem.
Popatrzmy, jak wygląda przykładowa implementacja schematu predyktor-korektor w przypadku schematów Eulera: otwartego schematu Eulera wziętego jako predyktor i zamkniętego schematu Eulera, który tu pełni rolę korektora dla równania
jako korektorem.
Popatrzmy, jak wygląda przykładowa implementacja schematu predyktor-korektor w przypadku schematów Eulera: otwartego schematu Eulera wziętego jako predyktor i zamkniętego schematu Eulera, który tu pełni rolę korektora dla równania ![]() z
z ![]() z rozwiązaniem
z rozwiązaniem ![]() . Zaimplementowaliśmy
powyższy schemat w octave biorąc
jako metodę iteracyjnego rozwiązywania równania nieliniowego w każdym kroku funkcję octave
. Zaimplementowaliśmy
powyższy schemat w octave biorąc
jako metodę iteracyjnego rozwiązywania równania nieliniowego w każdym kroku funkcję octave fsolve():
function [X,t]=predkoreuler(f,t0=0,x0=1,N=100,h=1.0/N) # Parametry funkcji: #f - wskaznik do pola wektorowego - funkcji dwóch argumentów f(x,t) # przy czym x0 - wektor pionowy dlugosc M; # przyklad definicji wskaznika do prostego pola wekt.: f=@(x,t) -x; #t0 - czas początkowy #h - stały krok dla schematu Eulera #N - ilość kroku schematu #Funkcja zwraca macierz X wymiaru (N+1)xM długości N+1 taka ze #X(k,:) jest przybliżeniem rozwiazania w punkcie czasu t0+(k-1)*h #oraz wektor t dlugosci N+1 z dyskretnymi punktami czasowymi global xx hh tt hh=h; M=length(x0); X=zeros(N+1,M); t=zeros(N+1,1); xx=X(1,:)=x0; tt=t(1)=t0; for k=2:N+1, xp=xx+h*f(xx,tt); #predyktor g=@(x) x - hh*f(x,tt) - xx; #funkcja pomocnicza dla zamkniętego schematu Eulera X(k,:)=xx=fsolve(g,xp); #rozwiązujemy równanie - korektor tt+=hh; t(k)=tt; endfor endfunction
6.4. Adaptacyjny dobór kroku całkowania
Stałe w twierdzeniach o zbieżności schematów są znacznie zawyżone i dobór kroku całkowania w oparciu o szacowania z tych twierdzeń jest niepraktyczny. Czy można jakoś oszacować błąd na bieżąco i zmieniać krok całkowania w zależności od tych oszacowań?
Załóżmy, że chcemy użyć konkretnego schematu jednokrokowego rzędu ![]() przybliżonego rozwiązywania
zadania początkowego (3.1)
takiego, że przy założeniu odpowiedniej gładkości
pola wektorowego
przybliżonego rozwiązywania
zadania początkowego (3.1)
takiego, że przy założeniu odpowiedniej gładkości
pola wektorowego ![]() otrzymujemy, że błąd metody
spełnia dla
otrzymujemy, że błąd metody
spełnia dla ![]() :
:
dla ![]() ,
, ![]() rozwiązania (3.1),
rozwiązania (3.1), ![]() rozwiązania przybliżonego obliczonego naszym schematem i pewnej funkcji
rozwiązania przybliżonego obliczonego naszym schematem i pewnej funkcji ![]() .
Można pokazać, że tak rzeczywiście jest, i że funkcja
.
Można pokazać, że tak rzeczywiście jest, i że funkcja ![]() jest rozwiązaniem odpowiedniego równania różniczkowego. Najważniejsze zaś jest to, że
jest rozwiązaniem odpowiedniego równania różniczkowego. Najważniejsze zaś jest to, że ![]() nie zależy od
nie zależy od ![]() .
Oznaczmy przez
.
Oznaczmy przez ![]() rozwiązanie otrzymane przy pomocy schematu dla ustalonego
rozwiązanie otrzymane przy pomocy schematu dla ustalonego ![]() i dla
i dla ![]() , a przez
, a przez
![]() oznaczmy błąd metody w punkcie
oznaczmy błąd metody w punkcie ![]() .
.
Wtedy
Postępując podobnie jak w ekstrapolacji Richardsona, jeśli odejmiemy stronami te równości to otrzymamy:
czyli otrzymujemy:
dla ![]() ,
a zatem:
,
a zatem:
Otrzymaliśmy w ten sposób estymator błędu.
Jeśli chcemy otrzymać błąd na poziomie ![]() i dla pewnego
i dla pewnego ![]() obliczyliśmy:
obliczyliśmy:
to możemy wyliczyć ![]() , dla którego błąd będzie na poziomie
, dla którego błąd będzie na poziomie ![]() , tzn.
przyjmując
, tzn.
przyjmując
otrzymujemy
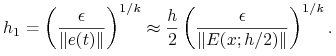 |
(6.2) |
Następnie możemy zastosować ten schemat z krokiem ![]() .
.
Oczywiście adapatacyjną zmianę kroku całkowania (ang. adaptive step control) można stosować i do zwiększania kroku w celu obniżania kosztu obliczeń.
To znaczy, że jeśli
![]() , to możemy zmniejszyć krok zgodnie z powyższym wzorem i wtedy
powtarzamy obliczenia z mniejszym krokiem
, to możemy zmniejszyć krok zgodnie z powyższym wzorem i wtedy
powtarzamy obliczenia z mniejszym krokiem ![]() . Jeśli
. Jeśli
![]() to za przybliżenie
to za przybliżenie ![]() weźmiemy
weźmiemy ![]() , a do następnego kroku możemy przyjąć nowy większy krok
, a do następnego kroku możemy przyjąć nowy większy krok ![]() z (6.2).
z (6.2).
Oczywiście zamiast połowienia kroku możemy obliczać ![]() dla
dla ![]() lub
lub ![]() i wtedy otrzymujemy analogiczne wzory.
i wtedy otrzymujemy analogiczne wzory.
Można też, zamiast stosowania tego samego schematu dwa razy z krokiem ![]() i potem
i potem ![]() ,
obliczać przybliżenie
,
obliczać przybliżenie ![]() , schematem rzędu
, schematem rzędu ![]() , a potem większego rzędu np.
, a potem większego rzędu np. ![]() ,
jak to się dzieje np. w metodzie Rungego-Fehlberga, gdzie stosuje się schematy Rungego-Kutty czwartego rzędu i Rungego-Kutty piątego rzędu, por. rozdział 17.2 w [24].
,
jak to się dzieje np. w metodzie Rungego-Fehlberga, gdzie stosuje się schematy Rungego-Kutty czwartego rzędu i Rungego-Kutty piątego rzędu, por. rozdział 17.2 w [24].
6.5. Metoda strzałów
Metoda strzałów (ang. shooting method) służy rozwiązywaniu zadań brzegowych. Rozpatrujemy w tym przypadku równanie różniczkowe zwyczajne, w którym
część warunków początkowych zastępujemy liniowymi lub nieliniowymi warunkami brzegowymi, tzn.
szukamy funkcji klasy ![]() na odcinku
na odcinku ![]() spełniającej:
spełniającej:
| (6.3) | |||||
dla ![]() danej funkcji co najmniej ciągłej.
danej funkcji co najmniej ciągłej.
Proszę zauważyć, że ogólnie takie zadanie nie musi mieć rozwiązania nawet w prostym przypadku np.
Rozwiązanie ogólne tego równania to ![]() i z powyższych warunków brzegowych otrzymujemy sprzeczne warunki na
i z powyższych warunków brzegowych otrzymujemy sprzeczne warunki na ![]() :
:
![]() i
i ![]() .
.
Jeśli istnieje rozwiązanie zadania brzegowego (6.3), to oczywiście jest to szczególny przypadek rozwiązania zadania początkowego (dla pewnej wartości ![]() ):
):
| (6.4) | |||||
Dodatkowo wiemy, że jeśli ![]() jest funkcją ciągłą, to wartość rozwiązania powyższego zadania początkowego dla
jest funkcją ciągłą, to wartość rozwiązania powyższego zadania początkowego dla ![]() , tzn.
, tzn.
![]() jest funkcją ciągłą względem
jest funkcją ciągłą względem ![]() . A jeśli
. A jeśli ![]() jest klasy
jest klasy ![]() , to
, to ![]() ma taką samą gładkość jak
ma taką samą gładkość jak ![]() , por. np. [23].
, por. np. [23].
Jeśli istnieje rozwiązanie (6.3), to dla pewnego ![]() zachodzi
zachodzi ![]() .
Sprowadziliśmy zadanie brzegowe do zadania nieliniowego znalezienia pierwiastka układu:
.
Sprowadziliśmy zadanie brzegowe do zadania nieliniowego znalezienia pierwiastka układu:
Do rozwiązania tego układu możemy zastosować jakąś metodę rozwiązywania układów równań nieliniowych, np. metodę bisekcji (o ile zadanie jest skalarne), czy metodę Newtona lub iteracji prostych, por. np. [18].
Można się spytać: jak obliczyć wartość ![]() dla danego
dla danego ![]() . Trzeba obliczyć
. Trzeba obliczyć ![]() , które jest wartością rozwiązania zadania początkowego (6.4) dla
, które jest wartością rozwiązania zadania początkowego (6.4) dla ![]() z warunkiem początkowym
z warunkiem początkowym ![]() .
.
Zwykle nie znamy rozwiązań ogólnych tego równania, więc musimy zastosować jakiś schemat rozwiązywania zadania początkowego.
Dla przykładu zastosowaliśmy metodę strzałów do rozwiązania zadania:
Wykorzystaliśmy metodę rozwiązywania równań zwyczajnych w octave lsode(),
w połączeniu z funkcją octave'a rozwiązywania równań nieliniowych fsolve().
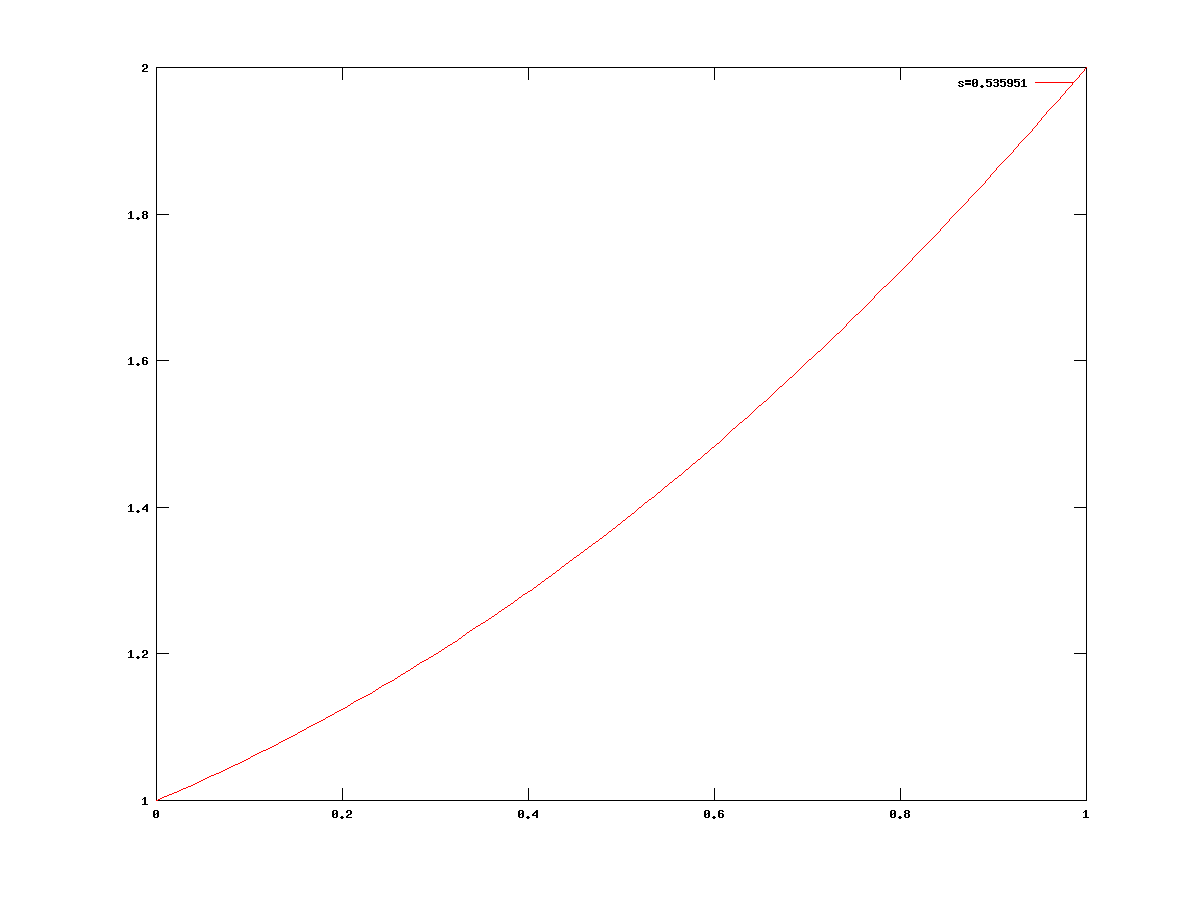
Otrzymaliśmy, że
dla ![]() błąd wynosi w przybliżeniu
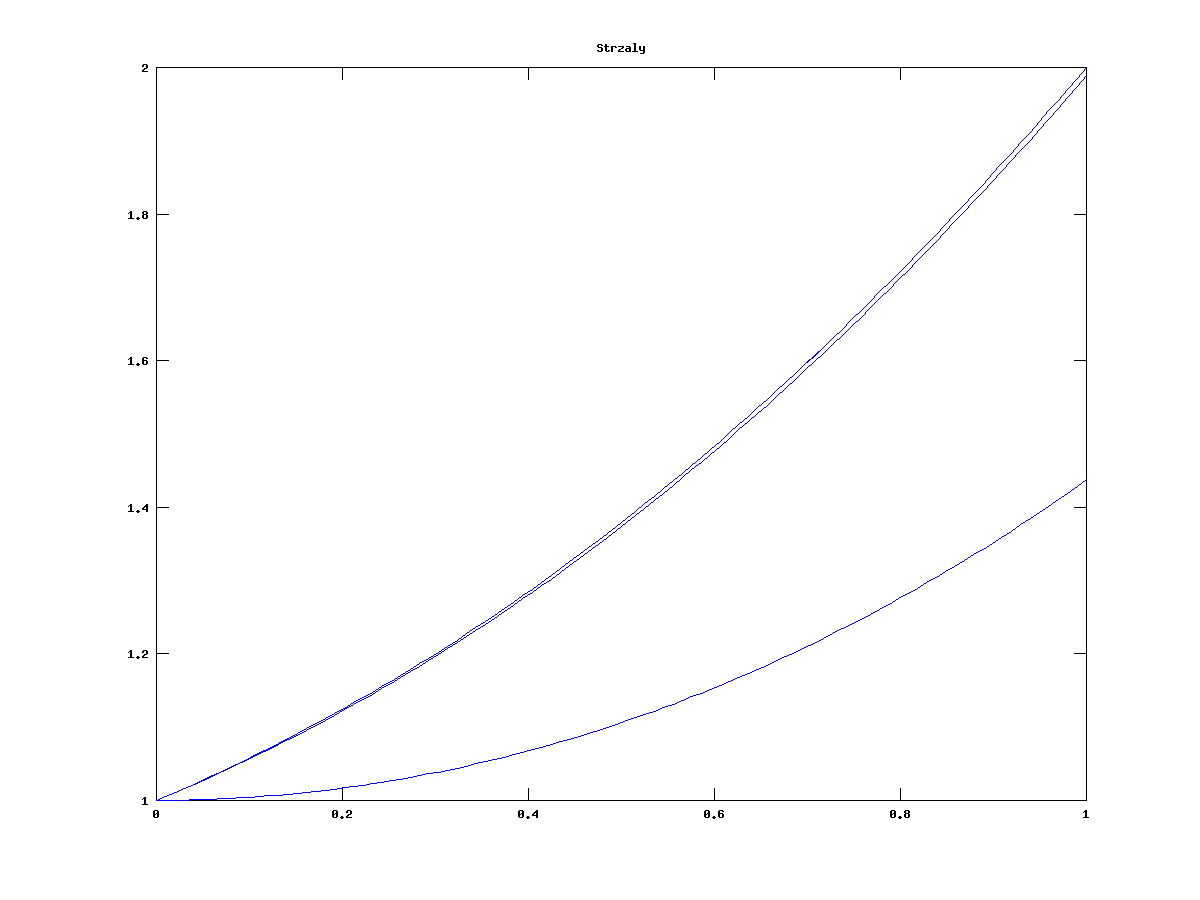
błąd wynosi w przybliżeniu ![]() . Na rysunku 6.1 widzimy wykres rozwiązania, a na rysunku 6.2
widać wykresy przybliżeń rozwiązania, tzn. rozwiązania zadania początkowego z
. Na rysunku 6.1 widzimy wykres rozwiązania, a na rysunku 6.2
widać wykresy przybliżeń rozwiązania, tzn. rozwiązania zadania początkowego z ![]() dla
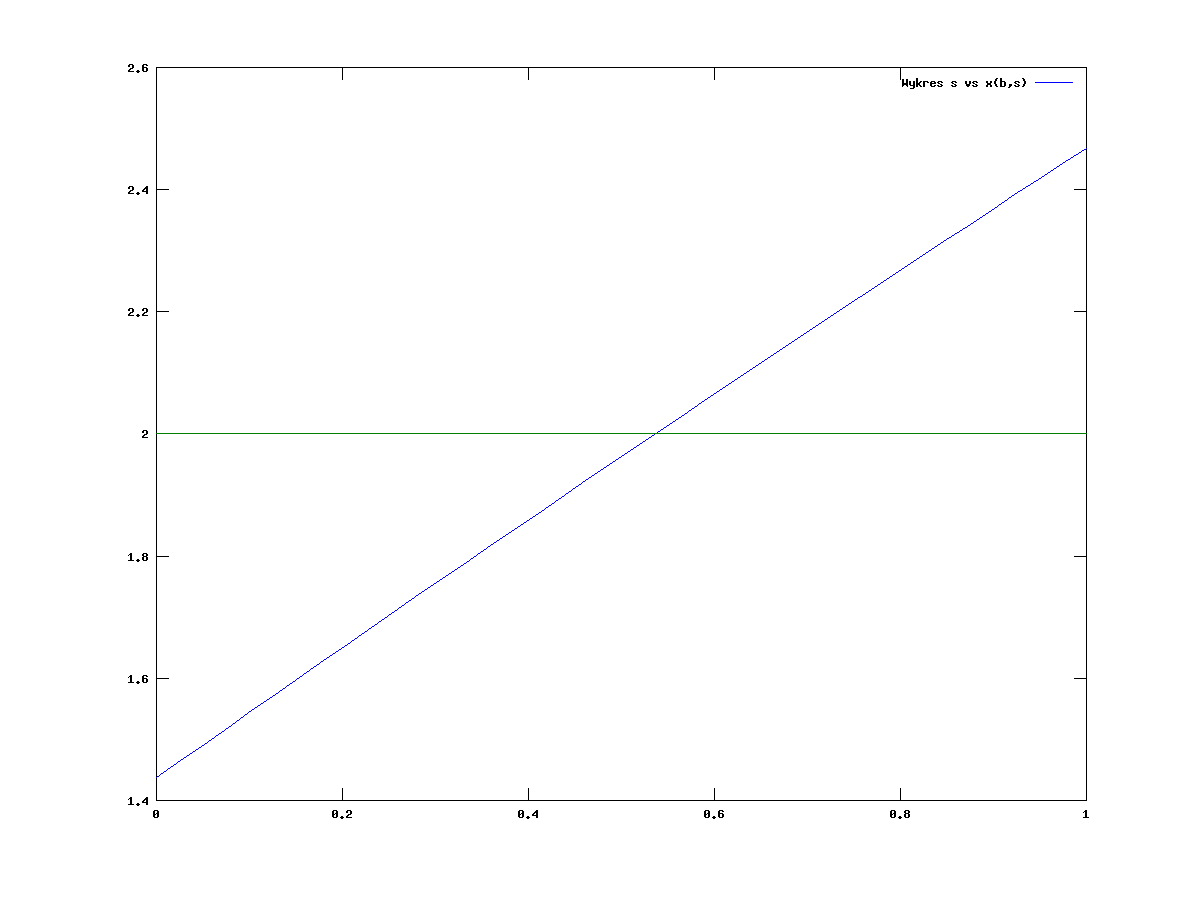
dla ![]() wartości kolejnych iteracji metody Newtona. Na rysunku 6.3
widzimy wykres funkcji
wartości kolejnych iteracji metody Newtona. Na rysunku 6.3
widzimy wykres funkcji ![]() .
.
Niestety metoda strzałów w wielu przypadkach może być bardzo niestabilna. Rozpatrzmy bardzo proste liniowe zadanie: ![]() z warunkami brzegowymi
z warunkami brzegowymi ![]() , dla którego znamy rozwiązanie
, dla którego znamy rozwiązanie ![]() . Zastosowanie metody strzałów z wykorzystaniem standardowej metody rozwiązywania równań zwyczajnych octave'a, czyli funkcją
. Zastosowanie metody strzałów z wykorzystaniem standardowej metody rozwiązywania równań zwyczajnych octave'a, czyli funkcją lsode(),
daje rozwiązanie przybliżone, dla którego błąd w ![]() wynosi ok.
wynosi ok. ![]() .
Wynika to z tego, że wartość rozwiązania zadania początkowego
.
Wynika to z tego, że wartość rozwiązania zadania początkowego ![]()
![]()
![]() dla
dla ![]() , tzn.
, tzn. ![]() , jest bardzo niestabilna. Małe zaburzenie
, jest bardzo niestabilna. Małe zaburzenie ![]() powoduje ogromną zmianę wyniku. W tym przypadku możemy funkcję
powoduje ogromną zmianę wyniku. W tym przypadku możemy funkcję ![]() , wyliczyć analitycznie, co pozostawiamy jako zadanie. Natomiast zastosowanie metody różnic skończonych daje dobre wyniki, por. rozdział 7.
, wyliczyć analitycznie, co pozostawiamy jako zadanie. Natomiast zastosowanie metody różnic skończonych daje dobre wyniki, por. rozdział 7.
6.6. Zadania
Ćwiczenie 6.1
Rozpatrzmy następujące zadanie brzegowe:
dla ![]() funkcji
funkcji ![]() .
.
-
Pokaż, że to zadanie ma jednoznaczne rozwiązanie dla stałego współczynnika
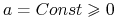 .
.
-
Przy założeniu, że współczynnik
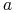 jest stały, wyznacz wszystkie wartości
jest stały, wyznacz wszystkie wartości 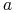 , dla których
powyższe zadanie może nie mieć rozwiązania.
, dla których
powyższe zadanie może nie mieć rozwiązania. -
Pokaż, że jeśli znamy rozwiązania zadania początkowego
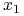 i
i 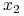 :
: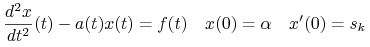
dla różnych
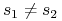 takie, że
takie, że 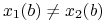 ,
to możemy wyznaczyć wzór na
,
to możemy wyznaczyć wzór na 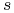 od
od 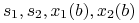 takie, że rozwiązanie zadania początkowego dla tego równania z warunkiem początkowym
takie, że rozwiązanie zadania początkowego dla tego równania z warunkiem początkowym 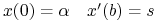 będzie rozwiązaniem wyjściowego zadania brzegowego.
będzie rozwiązaniem wyjściowego zadania brzegowego.
Ćwiczenie 6.2 (laboratoryjne)
Rozpatrzmy następujące zadanie brzegowe:
dla ![]() .
.
Zaimplementuj w octave metodę rozwiązywania zadania brzegowego
metodą strzałów korzystając z rozwiązania poprzedniego zadania.
W szczególności przetestuj dla ![]() i
i ![]() z warunkami brzegowymi
z warunkami brzegowymi ![]() dla
dla ![]() . Porównaj wynik z rozwiązaniem dokładnym
. Porównaj wynik z rozwiązaniem dokładnym ![]() .
.
Rozwiąż na odcinku ![]() korzystając z funkcji octave
korzystając z funkcji octave lsode() zadanie początkowe dla tego równania
z dwoma różnymi warunkami początkowym ![]() i
i ![]() dla
dla ![]() i
i ![]() . Następnie oblicz
. Następnie oblicz ![]() takie, że rozwiązanie zadania początkowego z
takie, że rozwiązanie zadania początkowego z
![]() i
i ![]() będzie rozwiązaniem wyjściowego zadania brzegowego.
będzie rozwiązaniem wyjściowego zadania brzegowego.
Ćwiczenie 6.3 (laboratoryjne)
Bazując na otwartym schemacie Eulera zaimplementuj w octave
schemat z adaptacyjnym krokiem całkowania korzystający ze wzoru (6.2)
w rozdziale 6.4.
Następnie dla równania ![]() z
z ![]() sprawdź błąd tego schematu dla
sprawdź błąd tego schematu dla ![]() i
i ![]() .
.
Ćwiczenie 6.4 (częściowo laboratoryjne)
Wyprowadź wzór analogiczny do (6.2) w rozdziale 6.4
dla schematu drugiego rzędu obliczając ![]() dla
dla ![]() , tzn. wzór na oszacowanie błędu bazujący na przybliżeniach
rozwiązania otrzymanych danym schematem dla
, tzn. wzór na oszacowanie błędu bazujący na przybliżeniach
rozwiązania otrzymanych danym schematem dla ![]() i
i ![]() .
Zastosuj otrzymane wzory dla zadania początkowego z poprzedniego zadania i schematu Heuna.
.
Zastosuj otrzymane wzory dla zadania początkowego z poprzedniego zadania i schematu Heuna.
Ćwiczenie 6.5
Udowodnij, że macierz ![]() dana wzorem (6.1) jest symetryczna, nieosobliwa i nieujemnie określona, czyli dodatnio określona.
dana wzorem (6.1) jest symetryczna, nieosobliwa i nieujemnie określona, czyli dodatnio określona.
Nieujemną określoność najprościej udowodnić z twierdzenia Gerszgorina, por. [17]. A nieosobliwość macierzy - wprost zakładając, że istnieje niezerowy wektor w jądrze macierzy i dochodząc do sprzeczności.
Ćwiczenie 6.6 (laboratoryjne)
Zaimplementuj w octave schemat predyktor-korektor biorąc za korektor
schemat trapezów rzędu dwa, a za predyktor schemat Heuna. Do rozwiązywania nieliniowego układu równań zastosuj
funkcję octave'a fsolve(). Przetestuj rząd takiego schematu metodą połowionego kroku, jak opisano w rozdziale 5.4, dla równania ![]() z
z ![]() dla
dla ![]() z rozwiązaniem
z rozwiązaniem ![]() i dla równania wahadła porównując z rozwiązaniem otrzymanym dla równania wahadła przy pomocy funkcji octave'a
i dla równania wahadła porównując z rozwiązaniem otrzymanym dla równania wahadła przy pomocy funkcji octave'a lsode().
Ćwiczenie 6.7 (laboratoryjne)
Zaimplementuj w octave schemat predyktor-korektor biorąc za korektor zamknięty schemat Eulera, a za predyktor otwarty schemat Eulera. Do rozwiązywania nieliniowego układu równań zastosuj swoje metody rozwiązywania równań nieliniowych tzn.:
-
metodę iteracji prostych, jak opisano w rozdziale 6.3,
-
wielowymiarową metodę Newtona.
Przetestuj rząd takiego schematu metodą połowionego kroku, jak opisano w rozdziale 5.4, dla równania ![]() z
z ![]() z rozwiązaniem
z rozwiązaniem ![]() dla
dla ![]() i dla równania wahadła porównując z rozwiązaniem otrzymanym dla równania wahadła przy pomocy funkcji octave'a
i dla równania wahadła porównując z rozwiązaniem otrzymanym dla równania wahadła przy pomocy funkcji octave'a lsode(). Porównaj czas i ilość iteracji potrzebne do wyliczenia ![]() każdą z tych metod przy tym samym warunku stopu metody.
każdą z tych metod przy tym samym warunku stopu metody.
Metoda Newtona rozwiązywania ![]() jest zdefiniowana następująco:
jest zdefiniowana następująco:
![]() dla
dla ![]() .
Układ równań liniowych
.
Układ równań liniowych ![]() możemy rozwiązać w octave przy użyciu operatora backslash tzn.
możemy rozwiązać w octave przy użyciu operatora backslash tzn. y=A \ b.