Zagadnienia
7. Metoda różnic skończonych dla równań eliptycznych drugiego rzędu
W tym rozdziale przedstawimy idee metody różnic skończonych na dwóch modelowych przykładach. Ze wszystkich metod przybliżonego rozwiązywania równań różniczkowych cząstkowych metoda ta wydaje się najbardziej intuicyjna w konstrukcji. W klasycznym sformułowaniu danego równania różniczkowego zamiast pochodnych rozpatrujemy ich przybliżenia. Na zadanej siatce rozpatrujemy przybliżenia pochodnych za pomocą różnic skończonych, czyli ilorazów różnicowych.
7.1. Modelowe zadanie jednowymiarowe
Rozpatrzmy następujące zagadnienie brzegowe:
| (7.1) | |||||
dla nieujemnej stałej ![]() , ustalonego odcinka
, ustalonego odcinka ![]() i znanych wartości
i znanych wartości ![]() .
.
Na podstawie tego modelowego zadania opiszemy ideę metody różnic skończonych (MRS).
Przyjmijmy następujące oznaczenia na różnicę skończoną w przód (ang. forward finite difference) i różnicę skończoną w tył (ang. backward finite difference) :
| (7.2) | |||||
dla ![]() . Będziemy często opuszczali dolny indeks
. Będziemy często opuszczali dolny indeks ![]() , jeśli
, jeśli ![]() będzie ustalone.
będzie ustalone.
Dla ustalonego kroku ![]() rozważmy następującą aproksymację drugiej pochodnej:
rozważmy następującą aproksymację drugiej pochodnej:
| (7.3) |
Nietrudno zauważyć, że jeśli funkcja ![]() jest klasy
jest klasy ![]() w otoczeniu
w otoczeniu ![]() to:
to:
| (7.4) |
co pozostawiamy jako zadanie, zob. ćwiczenie 7.1.
Wprowadzając siatkę (ang. mesh), czyli zbiór dyskretny dla ![]() :
:
z ![]() i
i ![]() ,
możemy zdefiniować następujące zadanie dyskretne:
znaleźć
,
możemy zdefiniować następujące zadanie dyskretne:
znaleźć ![]() funkcję określoną na siatce
funkcję określoną na siatce ![]() taką, że
taką, że
| (7.5) | |||||
| (7.6) |
Przyjmujemy, że ![]() przyjmuje wartości
przyjmuje wartości ![]() i
i ![]() .
.
Możemy przypuszczać, że ![]() będzie aproksymowało w jakimś sensie
będzie aproksymowało w jakimś sensie ![]() rozwiązanie zadania wyjściowego w punktach siatki.
rozwiązanie zadania wyjściowego w punktach siatki.
Jak porównać ![]() określone na zbiorze dyskretnym z
określone na zbiorze dyskretnym z ![]() określonym
na całym domknięciu obszaru?
Możemy porównać te funkcje w punktach siatki licząc błąd:
określonym
na całym domknięciu obszaru?
Możemy porównać te funkcje w punktach siatki licząc błąd:
dla ![]() funkcji obcięcia (ang. restriction) określonej na siatce, przyjmującej wartości
funkcji obcięcia (ang. restriction) określonej na siatce, przyjmującej wartości ![]() w punktach siatki,
ale możemy też badać dyskretną normę Euklidesową
w punktach siatki,
ale możemy też badać dyskretną normę Euklidesową ![]() , czyli pierwiastek z sumy kwadratów błędów w punktach siatki przeskalowanych przez
, czyli pierwiastek z sumy kwadratów błędów w punktach siatki przeskalowanych przez ![]() :
:
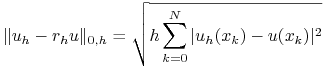 |
dla ![]() .
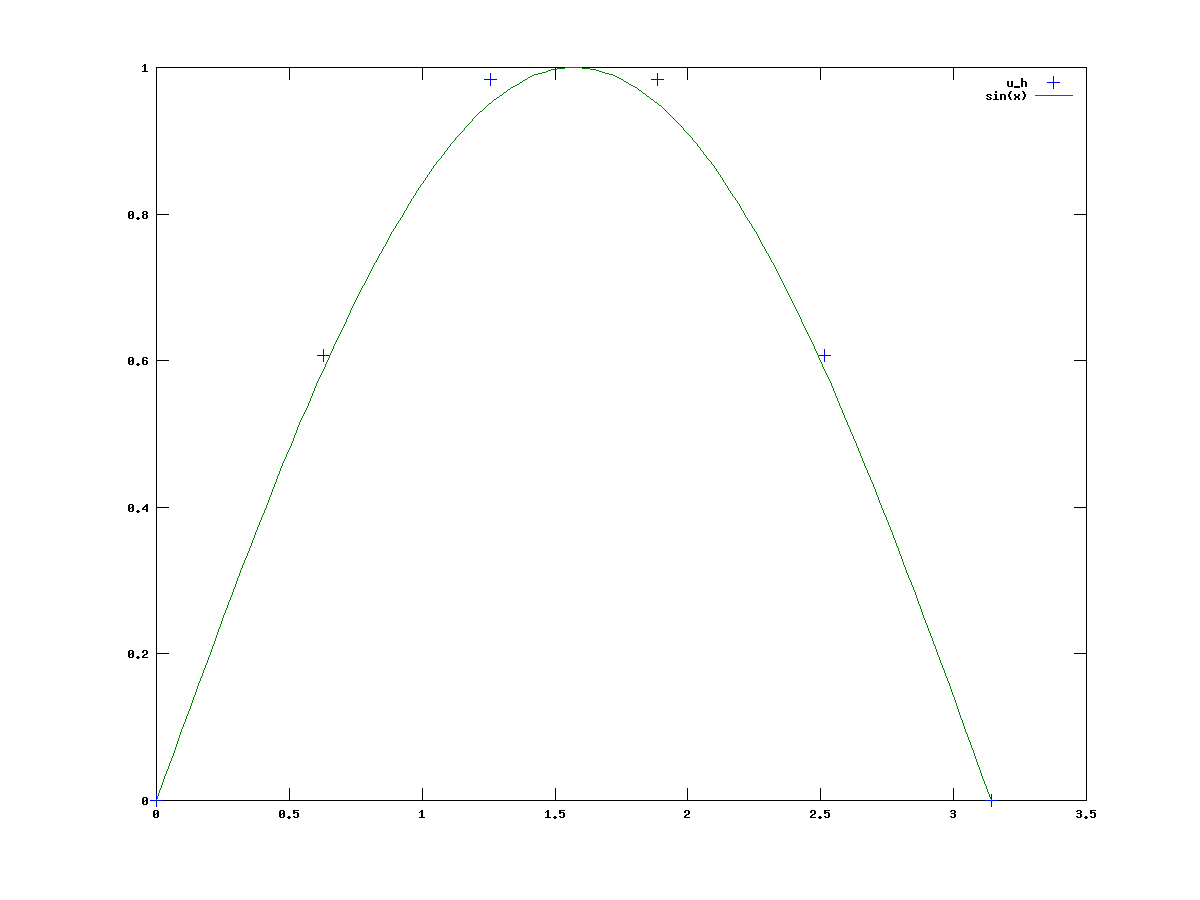
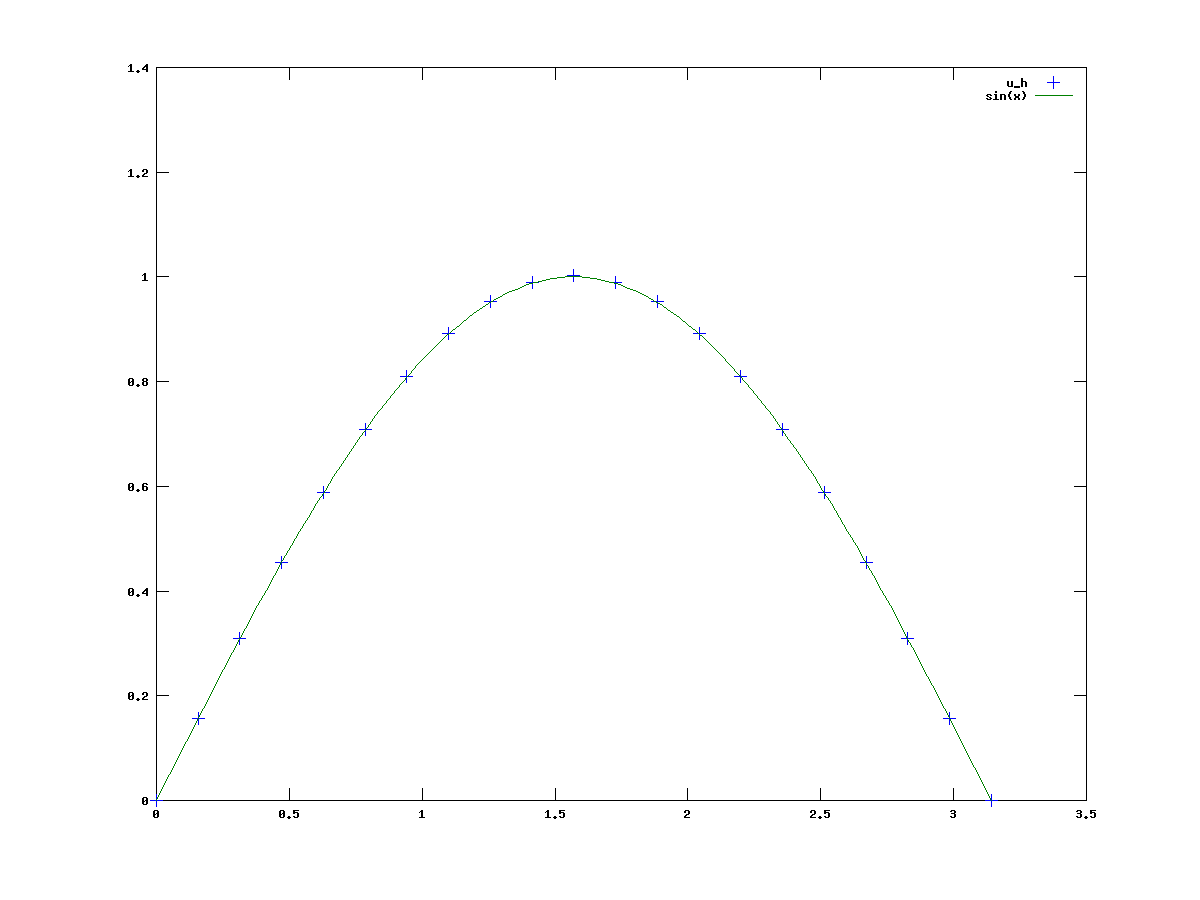
Popatrzmy na wykres rozwiązania zadania dyskretnego dla
.
Popatrzmy na wykres rozwiązania zadania dyskretnego dla ![]() i
i ![]() ,
dla którego rozwiązaniem jest
,
dla którego rozwiązaniem jest ![]() dla sześciu punktów i dla dwudziestu punktów, por. rysunki 7.1 i 7.2.
Widać, że dla dwudziestu punktów siatki rozwiązanie przybliżone pokrywa się
z rozwiązaniem dokładnym w punktach siatki.
dla sześciu punktów i dla dwudziestu punktów, por. rysunki 7.1 i 7.2.
Widać, że dla dwudziestu punktów siatki rozwiązanie przybliżone pokrywa się
z rozwiązaniem dokładnym w punktach siatki.
Będziemy badać błąd w normach ![]() i
i
![]() dla połowionych kroków, tzn. dla
dla połowionych kroków, tzn. dla ![]() dla ustalonego
dla ustalonego ![]() . Wyniki w tabeli 7.1 sugerują, że błędy dyskretne w obu normach są rzędu dwa, tzn. że
. Wyniki w tabeli 7.1 sugerują, że błędy dyskretne w obu normach są rzędu dwa, tzn. że ![]() i
i ![]() . W kolejnych rozdziałach wyjaśnimy dlaczego tak jest.
Jak się okaże wyniki eksperymentu są zgodne z oszacowaniami otrzymanymi teoretycznie.
. W kolejnych rozdziałach wyjaśnimy dlaczego tak jest.
Jak się okaże wyniki eksperymentu są zgodne z oszacowaniami otrzymanymi teoretycznie.
![\begin{array}[]{|l|c|c|c|c|}\hline N&\| e_{h}\| _{{\infty,h}}&\| e_{h}\| _{{\infty,h}}/\| e_{{2h}}\| _{{\infty,2h}}&\| e_{h}\| _{{0,h}}&\| e_{h}\| _{{0,h}}/\| e_{{2h}}\| _{{0,2h}}\\
\hline 10&8.265e-03&&1.036e-02&\\
20&2.059e-03&4.01e+00&2.580e-03&4.01e+00\\
40&5.142e-04&4.00e+00&6.445e-04&4.00e+00\\
80&1.285e-04&4.00e+00&1.611e-04&4.00e+00\\
160&3.213e-05&4.00e+00&4.027e-05&4.00e+00\\
320&8.032e-06&4.00e+00&1.007e-05&4.00e+00\\
640&2.008e-06&4.00e+00&2.517e-06&4.00e+00\\
1280&5.020e-07&4.00e+00&6.292e-07&4.00e+00\\
2560&1.255e-07&4.00e+00&1.573e-07&4.00e+00\\
5120&3.138e-08&4.00e+00&3.933e-08&4.00e+00\\
\hline\end{array}](wyklady/nrr/mi/mi939.png) |
Przyjmując oznaczenie ![]() otrzymujemy następujący układ równań liniowych:
otrzymujemy następujący układ równań liniowych:
![\begin{array}[]{rcl}u_{0}&=&g(a),\\
\frac{1}{h^{2}}(-u_{{k-1}}+2*u_{k}-u_{{k-1}})+c*u_{k}&=&f(x_{k})=f_{k}\qquad k=1,\ldots,N-1,\\
u_{N}&=&g(b).\end{array}](wyklady/nrr/mi/mi971.png) |
Wstawiając ![]() i
i ![]() do układu równań otrzymujemy następujący układ równań:
do układu równań otrzymujemy następujący układ równań:
![\frac{1}{h^{2}}\left(\begin{array}[]{rrrrr}2+c*h^{2}&-1&0&\cdots&0\\
-1&2+c*h^{2}&-1&\vdots\\
0&\ddots&\ddots&\ddots&\vdots\\
&&-1&2+c*h^{2}&-1\\
0&\cdots&0&-1&2+c*h^{2}\end{array}\right)\left(\begin{array}[]{c}u_{1}\\
u_{2}\\
\vdots\\
u_{{N-2}}\\
u_{{N-1}}\end{array}\right)=\left(\begin{array}[]{c}f_{1}+\frac{1}{h^{2}}g(a)\\
u_{2}\\
\vdots\\
u_{{N-2}}\\
u_{{N-1}}+\frac{1}{h^{2}}g(b)\end{array}\right),](wyklady/nrr/mi/mi935.png) |
(7.7) |
czyli układ z macierzą trójdiagonalną, który można rozwiązać np. metodą przeganiania
(wersja rozkładu LU dla macierzy trójdiagonalnej) kosztem
![]() dla
dla ![]() , czy nawet większych
, czy nawet większych ![]() (w zależności od dostępnego komputera).
(w zależności od dostępnego komputera).
7.2. Modelowe zadanie dwuwymiarowe
W tym rozdziale rozpatrzymy modelowe zadanie eliptyczne dwuwymiarowe na kwadracie jednostkowym
![]() .
Zadanie polega na
znalezieniu
.
Zadanie polega na
znalezieniu ![]() takiego, że
takiego, że
| (7.8) | |||||
gdzie ![]() ,
, ![]() jest ustaloną nieujemną stałą,
jest ustaloną nieujemną stałą, ![]() - to funkcja ciągła na
- to funkcja ciągła na ![]() , a
, a ![]() - to funkcja ciągła na
- to funkcja ciągła na ![]() . Zakładamy, że istnieje jednoznaczne rozwiązanie (7.8).
. Zakładamy, że istnieje jednoznaczne rozwiązanie (7.8).
Dla ustalonego kroku ![]() rozważmy następującą aproksymację drugiej pochodnej cząstkowej (por. (7.3)):
rozważmy następującą aproksymację drugiej pochodnej cząstkowej (por. (7.3)):
| (7.9) |
gdzie ![]() jest
jest ![]() -tym wersorem.
-tym wersorem.
Wprowadzamy siatkę (zbiór dyskretny) dla ![]() :
:
| (7.10) |
i jej odpowiednie podzbiory
![]() i
i ![]() .
.
Definiujemy następujące zadanie dyskretne: chcemy
znaleźć ![]() funkcję określoną na siatce
funkcję określoną na siatce ![]() taką, że
taką, że
![\left\{\begin{array}[]{rcl}-\sum _{{k=1,2}}\partial\overline{\partial}_{k}u_{h}(x)+c*u_{h}(x)&=&f(x)\qquad x\in\Omega _{h},\\
u(x)&=&g(x)\qquad x\in\partial\Omega _{h}\end{array}\right.](wyklady/nrr/mi/mi884.png) |
(7.11) |
Tak, jak w przypadku jednowymiarowym, możemy porównywać błąd w punktach siatki w dyskretnej normie maksimum:
dla ![]() zdefiniowanego analogicznie, tzn. funkcji określonej na siatce przyjmującej wartości
zdefiniowanego analogicznie, tzn. funkcji określonej na siatce przyjmującej wartości ![]() w punktach siatki lub
w dyskretnej normie
w punktach siatki lub
w dyskretnej normie ![]() :
:
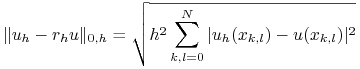 |
dla ![]() .
.
![\begin{array}[]{|l|c|c|c|c|}\hline N&\| z_{h}\| _{{\infty,h}}&\| z_{h}\| _{{\infty,h}}/\| z_{h}\| _{{\infty,2h}}&\| z_{h}\| _{{0,h}}&\| z_{h}\| _{{0,h}}/\| z_{h}\| _{{0,2h}}\\
\hline 10&5.211e-05&&2.789e-05&\\
20&1.317e-05&3.96e+00&7.011e-06&3.98e+00\\
40&3.298e-06&3.99e+00&1.755e-06&3.99e+00\\
80&8.254e-07&4.00e+00&4.389e-07&4.00e+00\\
160&2.064e-07&4.00e+00&1.097e-07&4.00e+00\\
\hline\end{array}](wyklady/nrr/mi/mi895.png) |
W Tabeli 7.2 podane są wyniki obliczeń dla dyskretyzacji (7.11)
zadania (7.8) z ![]() ze znanym rozwiązaniem
ze znanym rozwiązaniem ![]() i odpowiednio dobranymi
i odpowiednio dobranymi ![]() i
i ![]() dla
dla ![]() na brzegu kwadratu.
Stosunki norm dyskretnych dla danego
na brzegu kwadratu.
Stosunki norm dyskretnych dla danego ![]() względem błędu dla
względem błędu dla ![]() sugerują, że w tym przypadku widzimy
rząd zbieżności kwadratowej w obu normach, tzn.
że
sugerują, że w tym przypadku widzimy
rząd zbieżności kwadratowej w obu normach, tzn.
że ![]() i
i ![]() , tak samo jak w przypadku jednowymiarowym. Oczywiście obliczenia czyli rozwiązywanie odpowiedniego układu równań liniowych
jest teraz bardziej kosztowne, jako że np. dla
, tak samo jak w przypadku jednowymiarowym. Oczywiście obliczenia czyli rozwiązywanie odpowiedniego układu równań liniowych
jest teraz bardziej kosztowne, jako że np. dla ![]() czyli
czyli ![]() , otrzymujemy układ równań liniowych z
, otrzymujemy układ równań liniowych z
![]() niewiadomymi i z macierzą o
niewiadomymi i z macierzą o ![]() elementach. Jednak macierz jest pasmowa - o paśmie szerokości
elementach. Jednak macierz jest pasmowa - o paśmie szerokości ![]() i o około
i o około ![]() , czyli ma
, czyli ma ![]() niezerowych elementów.
Zatem możemy jeszcze zastosować specjalne, bezpośrednie metody rozwiązywania układów równań liniowych, takie jak
odpowiednia wersja rozkładu
niezerowych elementów.
Zatem możemy jeszcze zastosować specjalne, bezpośrednie metody rozwiązywania układów równań liniowych, takie jak
odpowiednia wersja rozkładu ![]() , por. np. [9], czy - jeśli trzymamy tę macierz w formacie rzadkim, np. spakowanych kolumn, czy wierszy - to możemy zastosować jakąś bezpośrednią metodę dla macierzy rzadkich, np. metodę frontalną, por. [8].
Warto zauważyć, że w tym szczególnym przypadku obszaru
, por. np. [9], czy - jeśli trzymamy tę macierz w formacie rzadkim, np. spakowanych kolumn, czy wierszy - to możemy zastosować jakąś bezpośrednią metodę dla macierzy rzadkich, np. metodę frontalną, por. [8].
Warto zauważyć, że w tym szczególnym przypadku obszaru ![]() znamy wartości i wektory własne tej macierzy i możemy zastosować specjalne metody rozwiązywania tego układu równań z wykorzystaniem algorytmu szybkiej transformaty Fouriera (FFT) (ang. Fast Fourier Transform), por. [10].
znamy wartości i wektory własne tej macierzy i możemy zastosować specjalne metody rozwiązywania tego układu równań z wykorzystaniem algorytmu szybkiej transformaty Fouriera (FFT) (ang. Fast Fourier Transform), por. [10].
Moglibyśmy też rozważyć siatkę ![]() z różnymi rozmiarami
z różnymi rozmiarami ![]()
![]() względem obu osi tzn.:
względem obu osi tzn.:
dla ![]() i
i ![]() i jej odpowiednie podzbiory
i jej odpowiednie podzbiory
![]() i
i ![]() .
.
Wtedy oczywiście otrzymalibyśmy trochę inny układ równań, ale generalnie o tych samych właściwościach.
7.2.1. Warunki brzegowe dla obszaru o skomplikowanej geometrii
Zauważmy, że dla obszaru ![]() możemy tak dobrać kroki siatki, aby
otrzymać w sposób naturalny punkty siatki leżące na
możemy tak dobrać kroki siatki, aby
otrzymać w sposób naturalny punkty siatki leżące na ![]() . W przypadku obszarów o bardziej skomplikowanej geometrii, które nie są prostokątami, czy sumami prostokątów, często nie ma takiej możliwości. Taka sytuacja ma miejsce np. gdy
. W przypadku obszarów o bardziej skomplikowanej geometrii, które nie są prostokątami, czy sumami prostokątów, często nie ma takiej możliwości. Taka sytuacja ma miejsce np. gdy ![]() jest kołem.
jest kołem.
Dla dowolnego ![]() i naszej aproksymacji różnicowej Laplasjanu wprowadzamy pomocniczą siatkę na
i naszej aproksymacji różnicowej Laplasjanu wprowadzamy pomocniczą siatkę na ![]() postaci
postaci
![]() dla
dla ![]() ustalonego punktu i
ustalonego punktu i ![]() dodatnich kroków.
Dla
dodatnich kroków.
Dla ![]() i naszego operatora różnicowego
i naszego operatora różnicowego ![]() definiujemy otoczenie siatkowe (ang. mesh neighborhood) punktu
definiujemy otoczenie siatkowe (ang. mesh neighborhood) punktu ![]() jako podzbiór
jako podzbiór ![]() taki, aby
taki, aby ![]() było zdefiniowane poprzez wartości
było zdefiniowane poprzez wartości ![]() w
w ![]() ,
czyli w tym przypadku otoczenie siatkowe
,
czyli w tym przypadku otoczenie siatkowe ![]() zawiera dany punkt
zawiera dany punkt ![]() i
cztery sąsiednie punkty leżące na pionowej i poziomej prostej przechodzącej przez
i
cztery sąsiednie punkty leżące na pionowej i poziomej prostej przechodzącej przez
![]() tzn.
tzn.
![]() ,
por. rysunek 7.4.
,
por. rysunek 7.4.
Wtedy definiujemy ![]() , a
, a
czyli
złożoną z takich punktów ![]() , że ten punkt i sąsiednie punkty na osiach siatki należą do
, że ten punkt i sąsiednie punkty na osiach siatki należą do ![]() .
Wtedy
.
Wtedy
![]() ,
por. rysunek 7.3.
(W przypadku bardziej skomplikowanych operatorów definicja
,
por. rysunek 7.3.
(W przypadku bardziej skomplikowanych operatorów definicja ![]() może być inna, a zatem i definicja
może być inna, a zatem i definicja ![]() może być inna).
może być inna).
Następnie będziemy szukali funkcji zdefiniowanej na tej siatce tj. w ![]() .
.
Zauważmy, że wtedy dla każdego ![]()
jest poprawnie zdefiniowany.
Pojawia się natomiast pytanie, jak postawić
warunek brzegowy Dirichleta w punktach ![]() , które nie leżą na
, które nie leżą na ![]() .
Najprostszym rozwiązaniem dla
.
Najprostszym rozwiązaniem dla ![]() , który leży w
, który leży w
![]() , jest postawienie w takim punkcie warunku:
, jest postawienie w takim punkcie warunku:
gdzie ![]() taki, że
odległość od
taki, że
odległość od ![]() jest nie większa niż
jest nie większa niż ![]() .
Dalej postępujemy jak w przypadku obszaru prostokątnego.
.
Dalej postępujemy jak w przypadku obszaru prostokątnego.
Rozwiązanie wyjściowego zadania ![]() jest określone we wszystkich punktach
jest określone we wszystkich punktach ![]() , ponieważ
, ponieważ ![]() . Operator obcięcia definiujemy tak samo, tzn.:
. Operator obcięcia definiujemy tak samo, tzn.:
Dla ![]() dostatecznie gładkiego otrzymujemy:
dostatecznie gładkiego otrzymujemy:
dla ![]() i tylko:
i tylko:
jeśli ![]() .
Pokazanie tego pozostawiamy jako zadanie.
.
Pokazanie tego pozostawiamy jako zadanie.
Oznacza to, że dokładność schematu na rozwiązaniu wyjściowego zagadnienia różniczkowego, czyli rząd aproksymacji schematu (który formalnie zostanie zdefiniowany w kolejnym rozdziale, por. definicja 8.4) wynosi jeden.
Istnieją oczywiście metody podwyższania rzędu aproksymacji w tym przypadku poprzez odpowiednią interpolację warunków brzegowych
z brzegu obszaru na punkty siatki ![]() leżące wewnątrz
leżące wewnątrz ![]() .
.
7.3. Zadania
Ćwiczenie 7.1
Udowodnij, (7.4).
Ćwiczenie 7.2
Rozpatrzmy zadanie różniczkowe jednowymiarowe:
czyli równanie
(7.5), ale z warunkiem brzegowym Neumanna :
tzn. z ![]() i
i ![]() .
Pokaż, że jeśli
.
Pokaż, że jeśli ![]() to zadanie ma jednoznaczne rozwiązanie.
to zadanie ma jednoznaczne rozwiązanie.
Rozważmy następującą dyskretyzację na siatce ![]() z
z ![]() i
i ![]() :
:
Sprawdź, czy to zadanie dyskretne ma jednoznaczne rozwiązanie. Sformułuj je jako układ równań liniowych:
dla ![]() ,
znajdując macierz
,
znajdując macierz ![]() i wektor prawej strony
i wektor prawej strony ![]() . Czy ta macierz jest symetryczna, czy jest nieosobliwa?
Czy jest trój-diagonalna? Jak rozwiązać powyższy układ możliwie małym kosztem?
. Czy ta macierz jest symetryczna, czy jest nieosobliwa?
Czy jest trój-diagonalna? Jak rozwiązać powyższy układ możliwie małym kosztem?
Ćwiczenie 7.3
Rozpatrzmy zadanie i schemat z poprzedniego zadania. Zbadaj, dla jakiego możliwie dużego ![]() lokalny błąd schematu posiada rząd
lokalny błąd schematu posiada rząd ![]() , czyli
, czyli
Zakładamy dowolnie wysoką regularność rozwiązania zadania wyjściowego.
Ćwiczenie 7.4
Rozpatrzmy zadanie różniczkowe i schemat z ćwiczenia 7.2, ale z ![]() . Pokaż, że zadanie nie ma jednoznacznego rozwiązania w ogólności, ale ma z dokładnością do stałej, o ile
. Pokaż, że zadanie nie ma jednoznacznego rozwiązania w ogólności, ale ma z dokładnością do stałej, o ile
![]() . Jaki warunek musi spełniać
. Jaki warunek musi spełniać ![]() , aby
zadanie dyskretne miało rozwiązanie?
Sformułuj ten schemat jako układ równań liniowych, jak w ćwiczeniu 7.2. Pokaż, że jądro macierzy
, aby
zadanie dyskretne miało rozwiązanie?
Sformułuj ten schemat jako układ równań liniowych, jak w ćwiczeniu 7.2. Pokaż, że jądro macierzy ![]() jest jednowymiarowe. Znajdź bazę jądra tej macierzy. Wykorzystując tę informację zaproponuj tanią (w sensie ilości operacji arytmetycznych) metodę znalezienia rozwiązania dyskretnego z dodatkowym warunkiem
jest jednowymiarowe. Znajdź bazę jądra tej macierzy. Wykorzystując tę informację zaproponuj tanią (w sensie ilości operacji arytmetycznych) metodę znalezienia rozwiązania dyskretnego z dodatkowym warunkiem ![]() .
.
Ćwiczenie 7.5
Analogicznie do przypadku jednowymiarowego, biorąc ![]() ,
,
i ![]() możemy zapisać zadanie dyskretne (7.11), jako układ równań liniowych
możemy zapisać zadanie dyskretne (7.11), jako układ równań liniowych
![]() z macierzą
z macierzą ![]() i wektorem prawej strony
i wektorem prawej strony ![]() . Wyznacz tę macierz i ten wektor (por. (7.7) dla przypadku jednowymiarowego).
Oblicz, ile elementów różnych od zera ma ta macierz. Policz, ile operacji arytmetycznych jest potrzebnych do rozwiązania tego układu równań liniowych z zastosowaniem metody Choleskiego, czyli rozkładu
. Wyznacz tę macierz i ten wektor (por. (7.7) dla przypadku jednowymiarowego).
Oblicz, ile elementów różnych od zera ma ta macierz. Policz, ile operacji arytmetycznych jest potrzebnych do rozwiązania tego układu równań liniowych z zastosowaniem metody Choleskiego, czyli rozkładu ![]() dla
dla ![]() macierzy dolnotrójkątnej w wersji dla macierzy pasmowych.
macierzy dolnotrójkątnej w wersji dla macierzy pasmowych.
Ćwiczenie 7.6 (laboratoryjne)
Stwórz w octavie macierz z poprzedniego zadania dla ![]() , tzn. macierz układu równań powstałego z (7.11), jako macierz pełną i rzadką (można wykorzystać funkcję octave'a
, tzn. macierz układu równań powstałego z (7.11), jako macierz pełną i rzadką (można wykorzystać funkcję octave'a sparse()). Następnie rozwiąż ten układ dla wektora prawej strony odpowiadającego funkcji ![]() dla
dla ![]() .
.
-
Korzystając z narzędzi octave'a
tic()itoc()sprawdź czas rozwiązywania dla różnych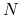 np.
np. 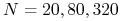 itp. dla obu typów macierzy. Czy różnica jest znacząca?
itp. dla obu typów macierzy. Czy różnica jest znacząca? -
Zbadaj błąd dyskretny w normie maksimum (funkcja octave'a
norm(wektor,'inf')) i w dyskretnej normie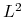 (np. używając funkcji octave'a
(np. używając funkcji octave'a norm(x,2)) między rozwiązaniem dokładnym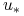 , a rozwiązaniem dyskretnym dla
, a rozwiązaniem dyskretnym dla 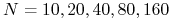 .
Czy eksperyment potwierdza teorię, tzn. czy dla podwojonych
.
Czy eksperyment potwierdza teorię, tzn. czy dla podwojonych 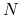 (czyli połowionych
(czyli połowionych 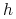 ) błąd maleje czterokrotnie?
) błąd maleje czterokrotnie?
Ćwiczenie 7.7 (laboratoryjne)
Rozwiąż równanie ![]() z warunkami brzegowymi
z warunkami brzegowymi ![]() na
na ![]() przy pomocy metody różnic skończonych, tzn. rozwiąż zadanie (7.1) dla
przy pomocy metody różnic skończonych, tzn. rozwiąż zadanie (7.1) dla ![]() i
i ![]() za pomocą schematu (7.5) dla
za pomocą schematu (7.5) dla ![]() . Policz normę maksimum w punktach siatki między dokładnymi wartościami rozwiązania
. Policz normę maksimum w punktach siatki między dokładnymi wartościami rozwiązania ![]() a rozwiązaniem dyskretnym
a rozwiązaniem dyskretnym ![]() zadania (7.5),
Porównaj z wynikami metody strzałów zastosowanej do tego zadania tj. z ćwiczeniem 6.2.
zadania (7.5),
Porównaj z wynikami metody strzałów zastosowanej do tego zadania tj. z ćwiczeniem 6.2.
Ćwiczenie 7.8 (częściowo laboratoryjne)
Rozpatrzmy przeskalowaną macierz z (7.7) (dla ![]() ):
):
![A_{{N-1}}=\left(\begin{array}[]{rrrrrr}2&-1&&&&\\
-1&2&-1&&&\\
&\ddots&\ddots&\ddots&&\\
&&-1&2&-1\\
&&&-1&2\\
\end{array}\right)\in\mathbb{R}^{{N-1,N-1}}](wyklady/nrr/mi/mi963.png) |
Pokaż, że jej wartości własne to ![]() dla
dla ![]() z odpowiednimi wektorami własnymi:
z odpowiednimi wektorami własnymi:
![]() dla
dla ![]() .
Oszacuj uwarunkowanie macierzy tzn.
.
Oszacuj uwarunkowanie macierzy tzn. ![]() dla
dla ![]() .
.
Porównaj z wynikami otrzymanymi przy pomocy funkcji octave'a eig() i cond().
Korzystamy z wzorów trygonometrycznych: ![]() oraz
oraz
![]() .
.
Zauważmy, że biorąc ![]() otrzymujemy, że
otrzymujemy, że
![]() . Zatem wystarczy sprawdzić, czy zachodzą równania
. Zatem wystarczy sprawdzić, czy zachodzą równania
![]() dla
dla ![]() .
.
Biorąc ![]() otrzymujemy:
otrzymujemy:
Uwarunkowanie ![]() dla dużych
dla dużych ![]() dąży do
nieskończoności jak
dąży do
nieskończoności jak ![]() .
.