Zagadnienia
8. Teoria zbieżności schematów różnicowych
W tym rozdziale przedstawimy ogólną teorię zbieżności schematów różnicowych, a następnie pokażemy m.in. zastosowanie tej teorii do przykładów z poprzedniego wykładu.
Osoby zainteresowane obszerniejszym przedstawieniem teorii różnic dzielonych odsyłamy do monografii [27].
8.1. Ogólna teoria zbieżności schematów różnicowych
W tym podrozdziale opiszemy ogólną teorię zbieżności schematów różnicowych. Ograniczymy się do szczegółowego omówienia przypadku schematów liniowych, tzn. aproksymacji równań różniczkowych liniowych.
Teoria ta potrzebna jest zarówno do badania zbieżności schematów różnicowych dla równań eliptycznych, jak i dla schematów dla innych typów równań, np. równań parabolicznych.
Załóżmy, że rozpatrujemy następujące zadanie różniczkowe:
chcemy znaleźć ![]() funkcję określoną na obszarze
funkcję określoną na obszarze ![]() taką, że
spełnia równanie różniczkowe z warunkami brzegowymi:
taką, że
spełnia równanie różniczkowe z warunkami brzegowymi:
| (8.1) | |||||
| (8.2) |
gdzie ![]() - to dane funkcje,
- to dane funkcje, ![]() - to operator różniczkowy liniowy,
- to operator różniczkowy liniowy, ![]() - to odpowiedni operator różniczkowy brzegowy liniowy określony na
- to odpowiedni operator różniczkowy brzegowy liniowy określony na ![]() dla
dla ![]() .
.
Będziemy zakładać, że powyższe zadanie jest poprawnie postawione, tzn. że
ma jednoznaczne rozwiązanie ![]() dla
dla ![]() przestrzeni liniowej funkcji określonych na
przestrzeni liniowej funkcji określonych na ![]() z normą
z normą ![]() .
Zakładamy też, że
.
Zakładamy też, że
dla ![]() przestrzeni funkcji określonych na
przestrzeni funkcji określonych na ![]() ,
a
,
a
dla ![]() przestrzeni funkcji określonych na
przestrzeni funkcji określonych na
![]() .
Wyjściowe zadanie różniczkowe możemy zapisać w postaci operatorowej jako:
znaleźć
.
Wyjściowe zadanie różniczkowe możemy zapisać w postaci operatorowej jako:
znaleźć ![]() takie, że
takie, że
| (8.3) | |||||
| (8.4) |
Zdefiniujmy ![]() jako siatkę, tzn. zbiór punktów izolowanych,
węzłów
należących do
jako siatkę, tzn. zbiór punktów izolowanych,
węzłów
należących do ![]() z parametrem
z parametrem ![]() .
.
Zakładamy, że istnieje rodzina siatek ![]() ,
czyli rodzina zbiorów punktów izolowanych należących do
,
czyli rodzina zbiorów punktów izolowanych należących do ![]() indeksowanych parametrem
indeksowanych parametrem ![]() , należącym do pewnego zbioru
, należącym do pewnego zbioru ![]() takim, że
takim, że ![]() (tzn. że istnieje podciąg siatek
(tzn. że istnieje podciąg siatek ![]() taki, że
taki, że ![]() ).
).
W praktyce najczęściej stosuje się siatki równomierne, tzn. podzbiory ![]() dla ustalonego punktu
dla ustalonego punktu ![]() . Ewentualnie stosuje się siatki o jednolitych krokach w danym kierunku w
. Ewentualnie stosuje się siatki o jednolitych krokach w danym kierunku w ![]() .
.
Siatkę ![]() przedstawiamy w postaci
przedstawiamy w postaci ![]() , gdzie
, gdzie ![]() będziemy nazywać zbiorem punktów siatkowych wewnętrznych (zazwyczaj zawartych w
będziemy nazywać zbiorem punktów siatkowych wewnętrznych (zazwyczaj zawartych w ![]() ), a
), a
![]() - zbiorem punktów siatkowych brzegowych (zawartych albo leżących w pobliżu
- zbiorem punktów siatkowych brzegowych (zawartych albo leżących w pobliżu ![]() ). W zbiorze
). W zbiorze ![]() punktów brzegowych możemy dalej wyróżniać podzbiory
punktów brzegowych możemy dalej wyróżniać podzbiory
![]() .
Zakładamy, że rodzina siatek
.
Zakładamy, że rodzina siatek ![]() jest gęsta w sensie następującej definicji:
jest gęsta w sensie następującej definicji:
Definicja 8.1
Rodzina siatek ![]() jest gęsta (ang. dense) w
jest gęsta (ang. dense) w ![]() , gdy dla dowolnego
, gdy dla dowolnego ![]() istnieje
istnieje ![]() takie, że dla
takie, że dla ![]() i dowolnego
i dowolnego ![]() kula
kula ![]() o środku w
o środku w ![]() i promieniu
i promieniu ![]() zawiera co najmniej jeden punkt
zawiera co najmniej jeden punkt
![]() .
.
Proszę zauważyć, że rodzina siatek zdefiniowana w Rozdziale 7.1 jest w sposób oczywisty gęsta dla ![]() .
.
Wprowadzamy teraz rodzinę zadań przybliżonych (schematów różnicowych), które dają się zapisać w następujący sposób:
chcemy
znaleźć funkcję ![]() określoną na
określoną na ![]() taką, że
taką, że
czy inaczej - operatorowo
| (8.5) | |||||
| (8.6) |
Zakładamy, że
![]() i
i ![]() dla
dla ![]() , gdzie:
, gdzie:
-
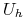 jest przestrzenią liniową unormowaną funkcji określonych na
jest przestrzenią liniową unormowaną funkcji określonych na 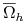 z normą
z normą 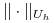 ,
, -
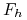 jest przestrzenią liniową unormowaną funkcji określonych na
jest przestrzenią liniową unormowaną funkcji określonych na 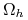 z normą
z normą 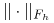 ,
, -
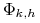 jest przestrzenią liniową unormowaną funkcji określonych na
jest przestrzenią liniową unormowaną funkcji określonych na 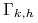 z normą
z normą 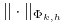 .
.
Zazwyczaj wszystkie rozpatrywane przestrzenie są zupełne, tzn. są przestrzeniami Banacha. W przypadku gdy ![]() jest ograniczony, są one też przestrzeniami skończenie wymiarowymi. Jeśli
jest ograniczony, są one też przestrzeniami skończenie wymiarowymi. Jeśli ![]() i wszystkie
i wszystkie ![]() są operatorami liniowymi, to mówimy, że rozpatrujemy zadanie przybliżone (dyskretne) liniowe, czy schemat różnicowy liniowy. W przeciwnym razie - gdy choć jeden z operatorów jest nieliniowy, to mamy do czynienia z zadaniem przybliżonym nieliniowym, czy schematem różnicowym nieliniowym.
są operatorami liniowymi, to mówimy, że rozpatrujemy zadanie przybliżone (dyskretne) liniowe, czy schemat różnicowy liniowy. W przeciwnym razie - gdy choć jeden z operatorów jest nieliniowy, to mamy do czynienia z zadaniem przybliżonym nieliniowym, czy schematem różnicowym nieliniowym.
Proszę zauważyć, że rozpatrujemy rodzinę zadań przybliżonych, parametryzowanych przez ![]() .
Tak, jak w przykładzie w Rozdziale 7.1, aby mówić o zbieżności rozwiązania zadania dyskretnego
.
Tak, jak w przykładzie w Rozdziale 7.1, aby mówić o zbieżności rozwiązania zadania dyskretnego ![]() do
do ![]() musimy mieć możliwość porównania obu funkcji. Dlatego
zakładamy, że istnieje rodzina operatorów obcięcia (ang. restriction)
musimy mieć możliwość porównania obu funkcji. Dlatego
zakładamy, że istnieje rodzina operatorów obcięcia (ang. restriction) ![]() , które są liniowe i ograniczone jednostajnie (ang.uniformly bounded) względem
, które są liniowe i ograniczone jednostajnie (ang.uniformly bounded) względem ![]() , tzn.
, tzn. ![]()
Operator obcięcia pozwala porównywać rozwiązania w normie przestrzeni dyskretnej, ale
możemy porównywać je również w normie przestrzeni ![]() . W tym celu musimy wprowadzić
rodzinę operatorów liniowych przedłużenia
. W tym celu musimy wprowadzić
rodzinę operatorów liniowych przedłużenia ![]() .
Najczęściej za operatory przedłużenia bierze się odpowiednie operatory interpolacji.
.
Najczęściej za operatory przedłużenia bierze się odpowiednie operatory interpolacji.
Uwaga 8.1
Można wprowadzić pojęcie zbieżności aproksymacji przestrzeni. Tzn.
rodzinę trójek ![]() nazywamy aproksymacją przestrzeni
nazywamy aproksymacją przestrzeni ![]() i mówimy, że
ta aproksymacja jest zbieżna, jeśli dla dowolnego
i mówimy, że
ta aproksymacja jest zbieżna, jeśli dla dowolnego ![]() zachodzi zbieżność
zachodzi zbieżność
W teorii zbieżności metod różnicowych najczęściej nie stosuje się operatorów przedłużenia, a za to wprowadza się warunek zgodności norm:
Definicja 8.2
Jeżeli dla danej przestrzeni unormowanej ![]() i rodziny przestrzeni unormowanych z odpowiednimi operatorami obcięcia
i rodziny przestrzeni unormowanych z odpowiednimi operatorami obcięcia ![]() zachodzi zbieżność
zachodzi zbieżność
to mówimy, że normy dyskretne ![]() są zgodne
(ang. consistent) z normą
są zgodne
(ang. consistent) z normą ![]() ,
,
Od tej pory będziemy zakładali zgodność norm dyskretnych z normą w ![]() , według powyższej definicji.
, według powyższej definicji.
Definicja 8.3
Zadanie przybliżone (zadanie dyskretne, schemat różnicowy) (8.5)-(8.6) jest zbieżne (czasami używa się terminu zbieżne dyskretnie) jeśli
gdzie ![]() - to rozwiązanie zadania (8.3)-(8.4), a
- to rozwiązanie zadania (8.3)-(8.4), a ![]() - to rozwiązanie dyskretne zadania przybliżonego (8.5)-(8.6).
- to rozwiązanie dyskretne zadania przybliżonego (8.5)-(8.6).
Jeśli dodatkowo zachodzi
to mówimy o zbieżności (dyskretnej) rzędu ![]() .
.
Wielkość ![]() będziemy nazywać błędem dyskretnym dla zadania przybliżonego (ang. dicrete error).
będziemy nazywać błędem dyskretnym dla zadania przybliżonego (ang. dicrete error).
Kolejnym krokiem jest wprowadzenie pojęcia aproksymacji zadania ciągłego (wyjściowego zadania różniczkowego) przez zadanie dyskretne.
Definicja 8.4 (aproksymacja; rząd schematu; (ang. consistency))
Mówimy, że zadanie przybliżone (8.5)-(8.6) aproksymuje zadanie (8.3)-(8.4), jeśli lokalne błędy aproksymacji zdefiniowane jako
dążą do zera dla ![]() . Tutaj
. Tutaj ![]() jest rozwiązaniem zadania (8.3)-(8.4), a
jest rozwiązaniem zadania (8.3)-(8.4), a
![]() są z zadania dyskretnego (8.5)-(8.6).
Jeśli dodatkowo zachodzi:
są z zadania dyskretnego (8.5)-(8.6).
Jeśli dodatkowo zachodzi:
to mówimy, że schemat aproksymuje (8.3)-(8.4) z rzędem ![]() (ang. local truncation error is of order
(ang. local truncation error is of order ![]() ),
(inaczej, że lokalne błędy aproksymacji są rzędu
),
(inaczej, że lokalne błędy aproksymacji są rzędu ![]() , dane zadanie przybliżone lub
schemat różnicowy ma rząd
, dane zadanie przybliżone lub
schemat różnicowy ma rząd ![]() , rząd aproksymacji schematu wynosi
, rząd aproksymacji schematu wynosi ![]() ).
).
Drugim ważnym pojęciem jest stabilność zadania dyskretnego. Tu podamy definicje stabilności dla schematu liniowego:
Definicja 8.5 (stabilność; (ang. stability))
Liniowe zadanie przybliżone (8.5)-(8.6) jest stabilne (poprawnie postawione), jeśli istnieje stała ![]() taka, że dla dowolnego
taka, że dla dowolnego ![]() ,
, ![]() i
dla dowolnych
i
dla dowolnych ![]() i
i ![]()
![]() zachodzą:
zachodzą:
-
rozwiązanie to spełnia następującą nierówność:
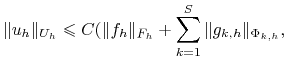
gdzie
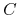 - to dodatnia stała niezależna od
- to dodatnia stała niezależna od 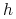 (ani oczywiście od
(ani oczywiście od 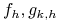 ).
).
Uwaga 8.2
W literaturze czasami za stabilność zadania przybliżonego przyjmuje się tylko warunek (2) z definicji 8.5.
Proszę zauważyć, że stabilność zadania przybliżonego jest samoistną cechą związaną tylko z definicją samego zadania dyskretnego- ona nie zależy w żaden sposób od rozwiązania równania różniczkowego.
Dodatkowo warto też zauważyć, że jeśli ![]() jest przestrzenią skończenie wymiarową,
istnieje rozwiązanie (8.5)-(8.6)
i spełniony jest warunek (2) z definicji 8.5, to wtedy to rozwiązanie jest
jednoznaczne.
jest przestrzenią skończenie wymiarową,
istnieje rozwiązanie (8.5)-(8.6)
i spełniony jest warunek (2) z definicji 8.5, to wtedy to rozwiązanie jest
jednoznaczne.
Sformułujemy teraz następujące twierdzenie o zbieżności zadania przybliżonego:
Twierdzenie 8.1 (Lax-Filipow)
Jeśli liniowe zadanie przybliżone (8.5)-(8.6) jest stabilne oraz aproksymuje
zadanie (8.3)-(8.4), którego rozwiązaniem jest ![]() , wtedy zadanie przybliżone jest zbieżne i
, wtedy zadanie przybliżone jest zbieżne i
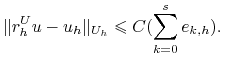 |
Z powyższego twierdzenia otrzymujemy od razu następujący wniosek:
Wniosek 8.1
Jeśli zadanie przybliżone (8.5)-(8.6) jest stabilne oraz aproksymuje
zadanie (8.3)-(8.4) z rzędem ![]() , to
, to
Oznaczmy ![]() .
Z liniowości
.
Z liniowości ![]() i
i ![]() dla
dla ![]() wynika, że
wynika, że
![]() spełnia zadanie przybliżone z odpowiednimi prawymi stronami:
spełnia zadanie przybliżone z odpowiednimi prawymi stronami:
zatem z definicji stabilności zadania przybliżonego otrzymujemy następujące oszacowanie:
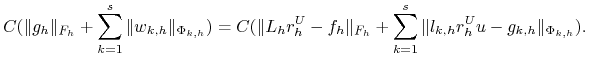 |
Następnie z faktu aproksymacji zadania (8.3)-(8.4) przez zadanie przybliżone (8.5)-(8.6) otrzymujemy ostatecznie oszacowanie:
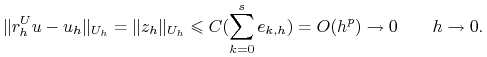 |
Powyższe twierdzenie można krótko podsumować, że aby otrzymać schemat zbieżny z rzędem ![]() musi być on stabilny i posiadać rząd aproksymacji
musi być on stabilny i posiadać rząd aproksymacji ![]() .
.
Proszę zauważyć, że twierdzenie jest bardzo ogólne, a dowód jest prosty. Pojawia się pytanie: jak dobrać odpowiednie przestrzenie i operatory, aby zadania przybliżone (schematy) były stabilne i miały możliwie wysoki rząd aproksymacji.
Uwaga 8.3
Proszę zauważyć, że powyższa teoria zbieżności może zostać zastosowana do zadań różniczkowych rożnego typu - zarówno eliptycznych, jak i parabolicznych, czy hiperbolicznych.
8.2. Zastosowanie teorii zbieżności do prostych schematów jedno- i dwuwymiarowych
8.2.1. Przypadek jednowymiarowy
Wracamy teraz do dyskretyzacji modelowego zadania jednowymiarowego (7.5)-(7.6).
Za przestrzeń ![]() weźmy przestrzeń funkcji ciągłych na
weźmy przestrzeń funkcji ciągłych na ![]() , czyli
, czyli ![]() z normą supremum
z normą supremum ![]() .
Oznaczmy przez
.
Oznaczmy przez ![]() zbiór funkcji określonych na dowolnym podzbiorze
zbiór funkcji określonych na dowolnym podzbiorze ![]() siatki
siatki
![]() z normą
z normą ![]() . Za przestrzeń dyskretną przyjmijmy
. Za przestrzeń dyskretną przyjmijmy
![]() .
Jeżeli wprowadzimy operatory
.
Jeżeli wprowadzimy operatory ![]() i
i
![]() zdefiniowane jako (por. (7.3)):
zdefiniowane jako (por. (7.3)):
dla ![]() i
i ![]() ,
to zadanie (7.5)-(7.6) możemy zapisać w formie operatorowej jako:
,
to zadanie (7.5)-(7.6) możemy zapisać w formie operatorowej jako:
| (8.7) | |||||
dla
![]() zdefiniowanego jako
zdefiniowanego jako ![]() dla
dla ![]() oraz
oraz ![]() z
z ![]() dla
dla ![]() .
.
W tym przypadku dla funkcji ciągłej przekształceniem obcięcia (ang. restriction) jest
![]() zdefiniowany jako
zdefiniowany jako
Możemy teraz zbadać zbieżność błędu dyskretnego:
dla ![]() , co jest równoważne badaniu zbieżności w punktach siatki.
Zauważmy, że otrzymujemy
, co jest równoważne badaniu zbieżności w punktach siatki.
Zauważmy, że otrzymujemy
co oznacza jednostajną ograniczoności operatorów obcięcia.
Można też w tym przypadku łatwo wprowadzić operator przedłużenia (ang. prolongation)
![]() Np. niech
Np. niech ![]() będzie funkcją ciągłą liniowo interpolującą wartości
będzie funkcją ciągłą liniowo interpolującą wartości
![]() pomiędzy punktami siatki tj.
pomiędzy punktami siatki tj.
Następnie możemy badać zbieżność błędu
![]() dla
dla ![]() . Jeśli błąd zbiega do zera, to
mówimy o zbieżności schematu w normie supremum.
. Jeśli błąd zbiega do zera, to
mówimy o zbieżności schematu w normie supremum.
Zauważmy, że w naszym przypadku dodatkowo zachodzi
| (8.8) |
czyli zbieżność aproksymacji przestrzeni wyjściowej przez przestrzeń dyskretną oraz
| (8.9) |
czyli zachodzi zgodność rodziny norm przestrzeni dyskretnych ![]() z normą przestrzeni wyjściowej
z normą przestrzeni wyjściowej ![]() .
Wykazanie tego pozostawiamy jako zadanie, por. ćwiczenie 8.1.
.
Wykazanie tego pozostawiamy jako zadanie, por. ćwiczenie 8.1.
Innym wyborem przestrzeni i norm jest badanie zbieżności i błędu w normie ![]() , czy odpowiednio dyskretnej normie
, czy odpowiednio dyskretnej normie ![]() definiowanej dla
definiowanej dla ![]() jako:
jako:
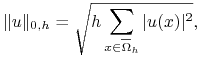 |
gdzie ![]() - to przestrzeń wszystkich funkcji określonych na
- to przestrzeń wszystkich funkcji określonych na ![]() .
Oczywiście zmieniliśmy oznaczenie przestrzeni funkcji dyskretnych na siatce. Jest to ten sam zbiór funkcji określonych na siatce, ale zmieniła się norma dyskretna.
.
Oczywiście zmieniliśmy oznaczenie przestrzeni funkcji dyskretnych na siatce. Jest to ten sam zbiór funkcji określonych na siatce, ale zmieniła się norma dyskretna.
Aby otrzymać zgodność norm powinniśmy inaczej zdefiniować obcięcia np. poprzez uśrednienia,
czyli ![]() dla
dla ![]() definiujemy:
definiujemy:
dla ![]() kuli o środku w
kuli o środku w ![]() i promieniu
i promieniu ![]() .
.
Inna możliwość to rozważenie zbioru funkcji ciągłych ![]() ale z normą
ale z normą ![]() , oraz normy dyskretnej typu
, oraz normy dyskretnej typu ![]() na
na ![]() . Następnie możemy przeprowadzić analizę z obcięciem
. Następnie możemy przeprowadzić analizę z obcięciem ![]() . Zbiór funkcji
. Zbiór funkcji
![]() z normą
z normą ![]() nie jest przestrzenią zupełną, ale jest gęstą podprzestrzenią przestrzeni
nie jest przestrzenią zupełną, ale jest gęstą podprzestrzenią przestrzeni ![]() .
.
Nietrudno zauważyć, że problem przybliżony aproksymuje problem wyjściowy z rzędem dwa, o ile rozwiązanie należy do ![]() , w obu powyżej przedstawionych przestrzeniach dyskretnych, czyli w odpowiednich normach dyskretnych.
Wykazanie, że schemat jest stabilny zarówno w
, w obu powyżej przedstawionych przestrzeniach dyskretnych, czyli w odpowiednich normach dyskretnych.
Wykazanie, że schemat jest stabilny zarówno w ![]() jak i
jak i ![]() jest trudniejsze. Zajmiemy się tym w kolejnych wykładach.
jest trudniejsze. Zajmiemy się tym w kolejnych wykładach.
8.2.2. Przypadek dwuwymiarowy
Rozpatrzmy ponownie modelowe zadanie dwuwymiarowe na kwadracie jednostkowym (7.8).
Analogicznie, jak w przypadku jednowymiarowym, niech ![]() z normą supremum
z normą supremum ![]() i
i ![]() będzie przestrzenią funkcji określonych na podzbiorze
będzie przestrzenią funkcji określonych na podzbiorze ![]() siatki
siatki
![]() (por. (7.10))
z normą
(por. (7.10))
z normą ![]() .
Przestrzeń dyskretną definiujemy jako
.
Przestrzeń dyskretną definiujemy jako
![]() .
.
Operator siatkowy (ang. mesh operator or discrete operator)
![]() i
brzegowy
i
brzegowy ![]() definiujemy jako:
definiujemy jako:
dla ![]() i
i ![]() .
Teraz zadanie (7.11) możemy zapisać w formie operatorowej jako
.
Teraz zadanie (7.11) możemy zapisać w formie operatorowej jako
| (8.10) |
dla funkcji prawej strony
![]() oraz
oraz ![]() zdefiniowanych jako
zdefiniowanych jako ![]() dla
dla ![]() i
i ![]() dla
dla ![]() .
Operatorem obcięcia (ang. restriction) jest
.
Operatorem obcięcia (ang. restriction) jest
![]() zdefiniowany jako
zdefiniowany jako
Tak samo jak w przypadku jednowymiarowym badamy błąd:
![]() lub w dyskretnej normie
lub w dyskretnej normie ![]() , tzn. w
, tzn. w
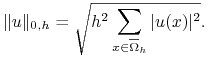 |
Tu ![]() jest zdefiniowana jako przestrzeń wszystkich funkcji określonych na
jest zdefiniowana jako przestrzeń wszystkich funkcji określonych na ![]() .
Oczywiście zbiór funkcji siatkowych jest ten sam, zmieniła się tylko norma.
.
Oczywiście zbiór funkcji siatkowych jest ten sam, zmieniła się tylko norma.
Można pokazać, że zachodzi zgodność norm dyskretnych z odpowiednimi normami, oraz że schemat (7.11) posiada rząd aproksymacji dwa i jest stabilny w obu normach dyskretnych. Wykazanie rzędu aproksymacji jest prostym zadaniem, natomiast pokazanie stabilności jest trudniejsze, por. rozdziały 9 i rozdział 10.
8.3. Zadania
Ćwiczenie 8.2
Zbadaj rząd lokalnych błędów aproksymacji schematu (8.7) dyskretyzacji modelowego problemu jednowymiarowego w obu normach dyskretnych.
Ćwiczenie 8.3
Wykaż, że rząd aproksymacji schematu (7.11) w dyskretnych normach maksimum i ![]() wynosi dwa, o ile rozwiązania wyjściowego zadania różniczkowego są dostatecznie gładkie.
wynosi dwa, o ile rozwiązania wyjściowego zadania różniczkowego są dostatecznie gładkie.
Ćwiczenie 8.4
Zbadaj rząd lokalnych błędów aproksymacji schematu (8.10) dyskretyzacji modelowego problemu dwuwymiarowego w obu normach dyskretnych.
Ćwiczenie 8.5
(Przybliżony warunek brzegowy) Rozpatrzmy modelowe zadanie jednowymiarowe z warunkiem brzegowym Dirichleta:
dla ![]() .
.
Rozpatrzmy następującą dyskretyzację zbudowaną na siatce ![]() dla
dla ![]() z
z ![]() z
z ![]() . Definiujemy
. Definiujemy ![]() i
i
![]() , oraz operatory:
, oraz operatory:
i
![]() . Zbadaj rząd lokalnego błędu aproksymacji tej dyskretyzacji w dyskretnej normie maksimum.
. Zbadaj rząd lokalnego błędu aproksymacji tej dyskretyzacji w dyskretnej normie maksimum.
Wystarczy zbadać błąd operatora brzegowego w punkcie ![]() . W pozostałych punktach błąd jest jak w schemacie (8.7).
. W pozostałych punktach błąd jest jak w schemacie (8.7).
Ćwiczenie 8.6
Rozważmy modelowe zadanie, jak i siatkę niezawierającą prawy koniec obszaru, tak jak w poprzednim ćwiczeniu.
Operatory ![]() i
i ![]() definiujemy tak samo, natomiast zmodyfikujmy operator brzegowy
definiujemy tak samo, natomiast zmodyfikujmy operator brzegowy ![]() w prawym końcu, tzn. w punkcie
w prawym końcu, tzn. w punkcie ![]() .
.
Rozpatrzmy tzw. aproksymację Collatza, tzn. niech wartość ![]() będzie liniowo interpolowała
warunek brzegowy w końcu obszaru:
będzie liniowo interpolowała
warunek brzegowy w końcu obszaru:
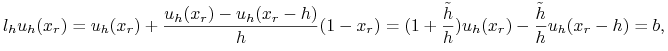 |
gdzie ![]() .
.
Zbadaj lokalny błąd aproksymacji tego schematu w normach dyskretnych maksimum i ![]() i jego rząd, tzn. czy zachowuje się jak
i jego rząd, tzn. czy zachowuje się jak ![]() dla pewnego
dla pewnego ![]() naturalnego.
naturalnego.
Ćwiczenie 8.7
Rozpatrzmy zadanie z poprzedniego ćwiczenia, ale z siatką nierównomierną:
![]() dla
dla ![]() z
z ![]() z
z ![]() .
Operator
.
Operator ![]() możemy zdefiniować jako
możemy zdefiniować jako
gdzie ![]() , ale musimy zmodyfikować definicję
, ale musimy zmodyfikować definicję ![]() , tzn.
, tzn.
i
Wyznacz ![]() w zależności od wartości
w zależności od wartości ![]() i
i ![]() tak, aby lokalny błąd aproksymacji schematu był możliwie mały.
tak, aby lokalny błąd aproksymacji schematu był możliwie mały.
Ćwiczenie 8.8
Rozpatrzmy zadanie jednowymiarowe ![]() na
na ![]() z warunkiem Neumanna
z warunkiem Neumanna
![]() . Rozpatrzmy następującą dyskretyzację zbudowaną na siatce
. Rozpatrzmy następującą dyskretyzację zbudowaną na siatce ![]() dla
dla ![]() z
z ![]() .
.
oraz
Zbadaj rząd lokalnego błędu aproksymacji tego schematu względem parametru siatki ![]() w dyskretnej normie maksimum i dyskretnej normie
w dyskretnej normie maksimum i dyskretnej normie ![]() .
.
Ćwiczenie 8.9
Rozpatrzmy zadanie jednowymiarowe ![]() na
na ![]() z warunkiem Neumanna
z warunkiem Neumanna
![]() . Rozpatrzmy następującą dyskretyzację o podwyższonym rzędzie
zbudowaną na siatce
. Rozpatrzmy następującą dyskretyzację o podwyższonym rzędzie
zbudowaną na siatce ![]() dla
dla ![]() z
z ![]() .
W punktach wewnętrznych siatki stosujemy standardowo aproksymacje na trzech punktach:
.
W punktach wewnętrznych siatki stosujemy standardowo aproksymacje na trzech punktach:
natomiast na brzegu podnosimy rząd schematu, a dokładniej zakładamy, że równanie jest spełnione w punktach brzegu, tzn.
funkcja ![]() jest określona na
jest określona na ![]() i
i ![]() dla
dla ![]() .
Rozpatrzmy lewy punkt brzegu
.
Rozpatrzmy lewy punkt brzegu ![]() . Widzimy, że
. Widzimy, że
o ile ![]() jest dostatecznie gładka. Zatem - korzystając z obu faktów - możemy skonstruować równanie różnicowe:
jest dostatecznie gładka. Zatem - korzystając z obu faktów - możemy skonstruować równanie różnicowe:
przybliżające warunek Neumanna w punkcie ![]() z wyższym rzędem.
z wyższym rzędem.
Skonstruuj analogiczne równanie różnicowe przybliżające warunek Neumanna w punkcie ![]() z wyższym rzędem.
Pokaż, że rząd lokalnego błędu aproksymacji tego schematu względem parametru siatki
z wyższym rzędem.
Pokaż, że rząd lokalnego błędu aproksymacji tego schematu względem parametru siatki ![]() wynosi dwa w dyskretnej normie maksimum i dyskretnej normie
wynosi dwa w dyskretnej normie maksimum i dyskretnej normie ![]() dla odpowiednio gładkiego rozwiązania.
Przetestuj w octavie rząd lokalnego błędu schematu w normie dyskretnej maksimum dla
dla odpowiednio gładkiego rozwiązania.
Przetestuj w octavie rząd lokalnego błędu schematu w normie dyskretnej maksimum dla ![]() metodą połowienia kroków.
metodą połowienia kroków.
Ćwiczenie 8.10
Rozpatrzmy modelowe zadanie dwuwymiarowe na kole o średnicy jeden tzn. (7.8) dla ![]() .
Dobierzmy siatkę na płaszczyźnie o parametrze
.
Dobierzmy siatkę na płaszczyźnie o parametrze ![]() równomierną zawierającą punkt
równomierną zawierającą punkt ![]() , tzn.
, tzn. ![]() .
.
Za ![]() uznajmy wszystkie punkty siatki, które należą do
uznajmy wszystkie punkty siatki, które należą do ![]() i wszystkie punkty przecięcia prostych zadających siatkę z brzegiem
i wszystkie punkty przecięcia prostych zadających siatkę z brzegiem
![]() . Te punkty przecięcia uznajemy za brzegowe punkty siatki. Otrzymujemy oczywiście siatkę nierównomierną, bo odległość między brzegowym punktem siatki, a jego sąsiadem wewnętrznym
jest mniejsza od
. Te punkty przecięcia uznajemy za brzegowe punkty siatki. Otrzymujemy oczywiście siatkę nierównomierną, bo odległość między brzegowym punktem siatki, a jego sąsiadem wewnętrznym
jest mniejsza od ![]() (poza ewentualnie pojedynczymi punktami).
(poza ewentualnie pojedynczymi punktami).
Tu warunek brzegowy możemy zadać dokładnie. Pojawia się pytanie: jak przybliżyć drugą pochodną w punktach wewnętrznych siatki, których punkty sąsiednie są na brzegu?
Definiujemy w takim punkcie ![]() (załóżmy, że tylko jego prawy sąsiad
(załóżmy, że tylko jego prawy sąsiad ![]() jest na brzegu):
jest na brzegu):
dla pewnych parametrów ![]() .
.
Jeśli ![]() ma dwa punkty sąsiednie leżące na brzegu (powiedzmy prawy i dolny punkt sąsiedni), tzn.
ma dwa punkty sąsiednie leżące na brzegu (powiedzmy prawy i dolny punkt sąsiedni), tzn. ![]() są na brzegu, to oczywiście musimy wyznaczyć całe równanie różnicowe:
są na brzegu, to oczywiście musimy wyznaczyć całe równanie różnicowe:
Zadanie: Wyznacz odpowiednie parametry ![]() , czy
, czy ![]() tak, aby lokalny błąd schematu
tak, aby lokalny błąd schematu ![]() był możliwie mały, tzn. żeby schemat posiadał możliwie wysoki rząd lokalnego błędu aproksymacji względem
był możliwie mały, tzn. żeby schemat posiadał możliwie wysoki rząd lokalnego błędu aproksymacji względem ![]() w dyskretnej normie maksimum.
w dyskretnej normie maksimum.




