Zagadnienia
7. Linie i okręgi
Podczas kursu matematyki obliczeniowej zetknęliśmy się z zadaniem: mając dany zestaw punktów na płaszczyźnie:
znaleźć prostą ![]() taką, że
taką, że
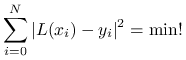 |
Było to po prostu inne sformułowanie liniowego zadania najmniejszych kwadratów na współczynniki ![]() . Zwróćmy jednak uwagę, że takie sformułowanie zadania nierówno traktuje zmienne
. Zwróćmy jednak uwagę, że takie sformułowanie zadania nierówno traktuje zmienne ![]() oraz
oraz ![]() .
.
W wielu zastosowaniach, na przykład: w analizie obrazów, w energetyce, czy w komunikacji, mamy do czynienia z zadaniem minimalizacji średniej odległości prostej od zestawu ![]() punktów na płaszczyźnie. Rzeczywiście, jest to matematyczne sformułowanie praktycznego zadania w rodzaju: Jak poprowadzić (prostą) autostradę tak, by dojazd do niej z pobliskich miejscowości był możliwie szybki? Albo: Jak, na podstawie nieco rozmytego konturu budynku na zdjęciu, zdefiniować jego brzeg?
punktów na płaszczyźnie. Rzeczywiście, jest to matematyczne sformułowanie praktycznego zadania w rodzaju: Jak poprowadzić (prostą) autostradę tak, by dojazd do niej z pobliskich miejscowości był możliwie szybki? Albo: Jak, na podstawie nieco rozmytego konturu budynku na zdjęciu, zdefiniować jego brzeg?
Przez analogię do zadania najmniejszych kwadratów określimy zadanie geometrycznego dopasowania prostej do punktów, polegające na wskazaniu takiej prostej ![]() , dla której
, dla której
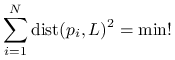 |
przy czym odległość będziemy mierzyć w normie euklidesowej.
Powyższe zadanie jest najprostszą wersją całej klasy zadań geometrycznego dopasowania, w których krzywą ![]() określonego typu chcemy dopasować do zadanego zestawu punktów
określonego typu chcemy dopasować do zadanego zestawu punktów ![]() tak, by
tak, by
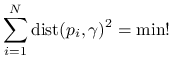 |
W przypadku budynków na przykład, szukalibyśmy prostokąta spełniającego powyższy warunek (por. uwagę na końcu wykładu). W niniejszym rozdziale zajmiemy się na początek, w oparciu o [6], geometrycznym dopasowaniem prostej, a w dalszej części wykładu, korzystając z materiałów zawartych w [1] — dopasowaniem okręgu do zadanych punktów.
Liczba punktów pomiarowych ![]() w praktyce nie jest bardzo duża, dlatego będziemy mieli do czynienia z zadaniami niezbyt intensywnymi obliczeniowo: głównym problemem będzie tutaj właściwe sformułowanie zadania w taki sposób, by można było je skutecznie zaatakować dostępnymi metodami.
w praktyce nie jest bardzo duża, dlatego będziemy mieli do czynienia z zadaniami niezbyt intensywnymi obliczeniowo: głównym problemem będzie tutaj właściwe sformułowanie zadania w taki sposób, by można było je skutecznie zaatakować dostępnymi metodami.
7.1. Dopasowanie prostej
Nietrudno zauważyć, że reprezentowanie prostej ![]() w postaci
w postaci ![]() nie jest zbyt zręczne, bo na przykład czasem najlepsze dopasowanie może zachodzić dla prostej
nie jest zbyt zręczne, bo na przykład czasem najlepsze dopasowanie może zachodzić dla prostej ![]() , której nie jesteśmy w stanie tak przedstawić. Dlatego korzystniej będzie rozpatrzyć ogólne równanie prostej
, której nie jesteśmy w stanie tak przedstawić. Dlatego korzystniej będzie rozpatrzyć ogólne równanie prostej ![]() postaci
postaci
oczywiście uzupełnione jakimś warunkiem normującym (współczynniki ![]() są dane z dokładnością do mnożnika). Tutaj najrozsądniej będzie przyjąć, że
są dane z dokładnością do mnożnika). Tutaj najrozsądniej będzie przyjąć, że ![]() : wektor
: wektor ![]() jest wektorem normalnym do prostej
jest wektorem normalnym do prostej ![]() .
Wtedy odległość punktu
.
Wtedy odległość punktu ![]() od
od ![]() jest dana równością
jest dana równością
zatem mamy znaleźć ![]() takie, że
takie, że ![]() oraz wyrażenie
oraz wyrażenie
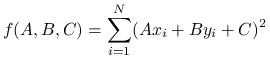 |
przyjmuje najmniejszą wartość.
7.1.1. Uproszczenia i analiza problemu
Ponieważ na parametr ![]() nie ma ograniczeń, możemy łatwo go wyeliminować z rozważań przyrównując do zera pochodną
nie ma ograniczeń, możemy łatwo go wyeliminować z rozważań przyrównując do zera pochodną
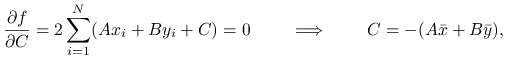 |
gdzie ![]() i analogicznie
i analogicznie ![]() .
.
W ten sposób zadanie zredukowało się do znalezienia wektora ![]() takiego, że
takiego, że
gdzie
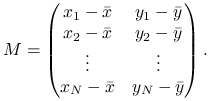 |
Jest to więc nic innego, jak zadanie wyznaczenia wektora szczególnego15Więcej na temat wektorów i wartości szczególnych można dowiedzieć się np. w wykładzie z Matematyki Obliczeniowej II, w rozdziale dotyczącym rozkładu SVD macierzy. macierzy ![]() , odpowiadającego najmniejszej wartości szczególnej. Rzeczywiście, jeśli
, odpowiadającego najmniejszej wartości szczególnej. Rzeczywiście, jeśli ![]() i macierze
i macierze ![]() są ortogonalne, a
są ortogonalne, a
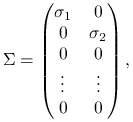 |
przy czym dla ustalenia uwagi ![]() , to
, to
a równość zachodzi gdy ![]() , czyli dla
, czyli dla ![]() .
.
7.1.2. Implementacja
Ponieważ w Octave znajduje się gotowa funkcja wyznaczająca pełny rozkład SVD zadanej macierzy, możemy pokusić się o implementację funkcji wyznaczenia ![]() na podstawie punktów, których współrzędne na osiach
na podstawie punktów, których współrzędne na osiach ![]() i
i ![]() podane są, odpowiednio, w talicach
podane są, odpowiednio, w talicach ![]() i
i ![]() :
:
function ABC = linefit(x,y) x = x(:); y = y(:); ABC = NaN(3,1); xm = mean(x); ym = mean(y); [U, S, V] = svd([x-xm, y-ym], 0); % ekonomiczny rozkład SVD ABC(1:2) = V(:,end); % [A, B] ABC(3) = - ABC(1)*xm - ABC(2)*ym; end
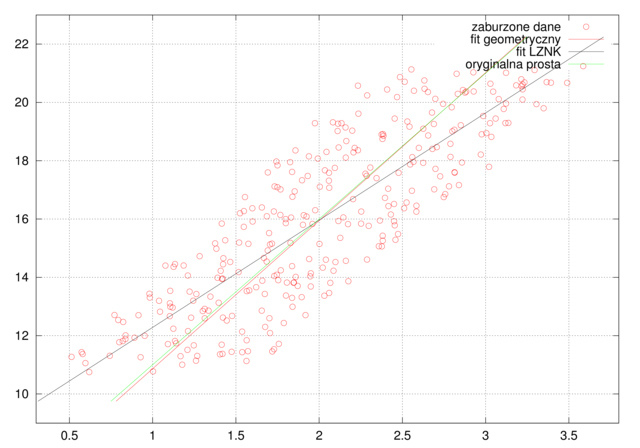
Aby przetestować działanie naszego kodu, zaburzymy losowo punkty prostej ![]() i sprawdzimy, co wyjdzie. Porównamy także nasz (geometryczny) fit z dopasowaniem na podstawie standardowej metody najmniejszych kwadratów.
i sprawdzimy, co wyjdzie. Porównamy także nasz (geometryczny) fit z dopasowaniem na podstawie standardowej metody najmniejszych kwadratów.
W celu wygodnego rysowania prostej zadanej w postaci uwikłanej, naprędce opracujemy funkcję lineplot, której listing zamieszczamy poniżej.
function lineplot(ABC, X, Y, color) if nargin < 4 color = ''; end xmin = X(1); xmax = X(2); ymin = Y(1); ymax = Y(2); A = ABC(1); B = ABC(2); C = ABC(3); if abs(A/B) <= 1 plot(X, (-C-A*X)/B, ['-',color]); else plot((-C-B*Y)/A, Y, ['-',color]); end end
Teraz możemy rozpocząć testy, korzystając na przykład z kodu poniższej postaci:
a = 5; b = 6;
x = linspace(1,3,300);
y = a*x + b;
x = x+0.6*(2*rand(size(x))-1);
y = y+0.6*(2*rand(size(y))-1);
% fit geometryczny
ABC = linefit(x,y);
% fit LZNK
ba = [ones(size(x)); x]'\y';
plot(x,y,'or');
hold on;
lineplot(ABC,[0,4],[min(y)-1,max(y)+1],'r');
lineplot([ba(2),-1,ba(1)],[0,4],[min(y)-1,max(y)+1],'k');
lineplot([a,-1,b],[0,4],[min(y)-1,max(y)+1],'g');
hold off;
legend('zaburzone dane','fit geometryczny','fit LZNK','oryginalna prosta');
grid on;
7.2. Dopasowanie okręgu
Analogicznie, można rozważyć zadanie geometrycznego dopasowania okręgu (lub, w większej ogólności, elipsy) ![]() do danych punktów na płaszczyźnie. Zastosowania mogą dotyczyć [1] medycyny (zwłaszcza — okulistyki), kontroli jakości wykonania obrotowych części mechanicznych, wyznaczania torów cząstek elementarnych, robotyki, a nawet — archeologii (wyznaczenie średnicy stadionu na podstawie zachowanych fragmentów). W wymienionych przypadkach zazwyczaj mamy do czynienia z zestawem punktów znajdujących się na łuku stanowiącym jedynie niewielki fragment okręgu. Z powodu zaburzeń danych, spowodowanych na przykład błędami pomiaru, zadane punkty nie układają się idealnie na poszukiwanej krzywej.
do danych punktów na płaszczyźnie. Zastosowania mogą dotyczyć [1] medycyny (zwłaszcza — okulistyki), kontroli jakości wykonania obrotowych części mechanicznych, wyznaczania torów cząstek elementarnych, robotyki, a nawet — archeologii (wyznaczenie średnicy stadionu na podstawie zachowanych fragmentów). W wymienionych przypadkach zazwyczaj mamy do czynienia z zestawem punktów znajdujących się na łuku stanowiącym jedynie niewielki fragment okręgu. Z powodu zaburzeń danych, spowodowanych na przykład błędami pomiaru, zadane punkty nie układają się idealnie na poszukiwanej krzywej.
Jeśli okrąg ![]() reprezentować przez środek
reprezentować przez środek ![]() oraz promień
oraz promień ![]() :
:
to odległość ![]() zadanego punktu
zadanego punktu ![]() od
od ![]() jest równa, jak łatwo sprawdzić,
jest równa, jak łatwo sprawdzić,
W takim razie, musimy zminimalizować wartość funkcjonału
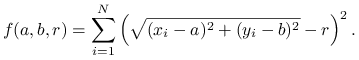 |
7.2.1. Atak na wprost
Ponieważ zadanie minimalizacji tym razem dotyczy bardziej skomplikowanego funkcjonału nieliniowego, użyjemy standardowej procedury optymalizacji nieliniowej w Octave, sqp.
function d = residgeom(X,x,y) % a = X(1); b = X(2); r = X(3); d = sumsq( sqrt((x-X(1)).^2 + (y-X(2)).^2) - X(3)); end function [S,dist,info] = fitcircle1(S0,x,y) % S = (a,b,r) [S,dist,info] = sqp(S0,@(X)residgeom(X,x,y)); end
Funkcja residgeom wyznacza wartość funkcjonału ![]() , przy czym przekazujemy jej wszystkie parametry funkcjonału w pierwszym argumencie, w postaci wektora
, przy czym przekazujemy jej wszystkie parametry funkcjonału w pierwszym argumencie, w postaci wektora X. Musimy tak zrobić, bo sqp spodziewa się funkcji jednego argumentu — taką tworzymy w postaci funkcji anonimowej
@(X)residgeom(X,x,y)przekazywanej do
sqp. Ponieważ w zadaniu nieliniowym wymagany jest sensowny punkt startowy fitcircle1. Zadaniem użytkownika jest właściwy dobór 7.2.2. Zmiana sformułowania zadania
Jakkolwiek dokonany przez nas wybór parametrów zadania: ![]() , jest niewątpliwie kuszący, to jednak, gdy punkty
, jest niewątpliwie kuszący, to jednak, gdy punkty ![]() są prawie współliniowe, wyznaczany promień
są prawie współliniowe, wyznaczany promień ![]() może być bardzo duży w porównaniu do współrzędnych środka
może być bardzo duży w porównaniu do współrzędnych środka ![]() . Ponadto małe zaburzenia położenia punktów
. Ponadto małe zaburzenia położenia punktów ![]() mogą prowadzić do dużych skoków wielkości
mogą prowadzić do dużych skoków wielkości ![]() (a także — położenia środka okręgu), dlatego warto zadanie sformułować inaczej.
(a także — położenia środka okręgu), dlatego warto zadanie sformułować inaczej.
Okrąg ![]() możemy opisać za pomocą standardowego równania krzywej drugiego stopnia,
możemy opisać za pomocą standardowego równania krzywej drugiego stopnia,
Ponieważ wynika stąd, że
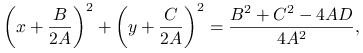 |
Jak podaje [1], Pratt zasugerował warunek normalizacyjny
Ponadto wówczas odległość ![]() punktu
punktu ![]() od okręgu jest równa
od okręgu jest równa
zatem musimy minimalizować funkcjonał
z ograniczeniem
To zadanie po raz kolejny zrealizujemy za pomocą funkcji sqp:
function d = residgeom2(X,x,y) A = X(1); B = X(2); C = X(3); D = X(4); P = A*(x.^2 +y.^2) + B*x + C*y + D; d = sumsq(2*(P./(1+sqrt(1+4*A*P)))); end function d = constr(X) d = X(2)^2 + X(3)^2 - 4*X(1)*X(4) - 1; end function [S,dist,info] = fitcircle2(S0,x,y) % S = (A,B,C,D) c = zeros(4,1); c(1) = 1/(2*S0(3)); c(2:3) = -2*c(1)*S0(1:2); c(4) = (c(2)^2 + c(3)^2 - 1)/(4*c(1)); [c,dist,info] = sqp(c, @(X)residgeom2(X,x(:),y(:)), @constr); S = [-c(2:3)/(2*c(1)); sqrt(c(2)^2 + c(3)^2 - 4*c(1)*c(4))/(2*abs(c(1)))]; end
Jakkolwiek ostatnią linijkę kodu moglibyśmy teoretycznie zastąpić tańszym
S = [-c(2:3); 1]/(2*c(1)), to jednak bezpieczniej będzie zrobić tak, jak powyżej — bo warunek ![]() może nie być idealnie spełniony.
może nie być idealnie spełniony.
7.2.3. Wybór przybliżenia początkowego jako nowe zadanie
Pozostaje jeszcze pytanie, w jaki sposób będziemy mogli sensownie wyznaczyć początkowe przybliżenie ![]() . Nadspodziewanie dobrym kandydatem na
. Nadspodziewanie dobrym kandydatem na ![]() jest (patrz [1]) okrąg spełniający tzw. algebraiczny warunek dopasowania, tzn. minimalizujący, przy ograniczeniu
jest (patrz [1]) okrąg spełniający tzw. algebraiczny warunek dopasowania, tzn. minimalizujący, przy ograniczeniu ![]() , sumę kwadratów residuum równania okręgu:
, sumę kwadratów residuum równania okręgu:
gdzie ![]() jest zadane przez
jest zadane przez ![]() .
.
Jest to więc — bardzo podobnie jak widzieliśmy to w przypadku fitowania prostej — zadanie najmniejszych kwadratów dla ![]()
gdzie
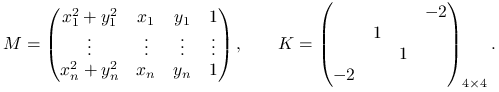 |
Niestety, macierz ![]() nie jest dodatnio określona, co komplikuje algorytm rozwiązywania tego zadania.
nie jest dodatnio określona, co komplikuje algorytm rozwiązywania tego zadania.
Funkcja Lagrange'a jest postaci
zatem koniecznym warunkiem dla ekstremum jest
Ponieważ ![]() , to pierwszy warunek oznacza po prostu, że para
, to pierwszy warunek oznacza po prostu, że para ![]() jest parą własną powyższego uogólnionego zadania własnego,
jest parą własną powyższego uogólnionego zadania własnego,
| (7.1) |
Wprowadzając (ekonomiczny) rozkład QR macierzy ![]() ,
,
mamy równoważnie ![]() i stąd
i stąd ![]() musi być parą własną macierzy
musi być parą własną macierzy ![]() .
Ponieważ macierz
.
Ponieważ macierz ![]() ma wartości własne
ma wartości własne ![]() , to macierz
, to macierz ![]() (na mocy tw. Sylvestera) także ma dokładnie jedną wartość własną ujemną, a pozostałe trzy — dodatnie.
(na mocy tw. Sylvestera) także ma dokładnie jedną wartość własną ujemną, a pozostałe trzy — dodatnie.
Mnożąc stronami (7.1) przez ![]() dostajemy
dostajemy
na mocy warunku ![]() . Ponieważ
. Ponieważ ![]() , interesująca nas
, interesująca nas ![]() nie może być ujemna. Ze względu na to, że poszukiwane przez nas
nie może być ujemna. Ze względu na to, że poszukiwane przez nas ![]() musi minimalizować
musi minimalizować ![]() , znaczy to, że minimum zostanie przyjęte równe najmniejszej dodatniej wartości własnej
, znaczy to, że minimum zostanie przyjęte równe najmniejszej dodatniej wartości własnej ![]() . W takim razie szukana przez nas para własna to para odpowiadająca najmniejszej dodatniej wartości własnej macierzy
. W takim razie szukana przez nas para własna to para odpowiadająca najmniejszej dodatniej wartości własnej macierzy ![]() .
.
Stąd jednym ze sposobów implementacji powyższego algorytmu wyznaczenia ![]() — a tym samym okręgu spełniającego wymieniony na początku tej sekcji algebraiczny warunek dopasowania — może być funkcja:
— a tym samym okręgu spełniającego wymieniony na początku tej sekcji algebraiczny warunek dopasowania — może być funkcja:
function [S,dist,info] = fitcircle3(x,y)
x = x(:); y = y(:);
invB = [0 0 0 -0.5; 0 1 0 0; 0 0 1 0; -0.5 0 0 0]; % $B^{-1}$ explicite
X = [x.^2+y.^2, x, y, ones(size(x))];
[Q R] = qr(X,0);
[V L] = eig(R*invB*R');
[L i] = sort(diag(L));
c = R \ V(:,i(2)); % interesuje nas druga najmniejsza w.wl, a raczej: wektor
S = [-c(2:3)/(2*c(1)); sqrt(c(2)^2 + c(3)^2 - 4*c(1)*c(4))/(2*abs(c(1)))];
dist = residgeom(S,x,y);
info = 1;
end
Ćwiczenie 7.1
Przeredaguj funkcje fitcircle1 i fitcircle2 tak, by jeśli użytkownik nie poda przybliżenia startowego, zostało wybrane przybliżenie wyznaczanie funkcją fitcircle3.
Musimy zmienić kolejność argumentów tak, by przybliżenie początkowe było ostatnim. Wtedy początek funkcji, np. fitcircle1, należałoby zapisać np. w takiej formie:
function [S,dist,info] = fitcircle1(x,y,S0) if nargin < 3 S0 = fitcircle3(x,y); end % ... tu dalsze instrukcje ... end
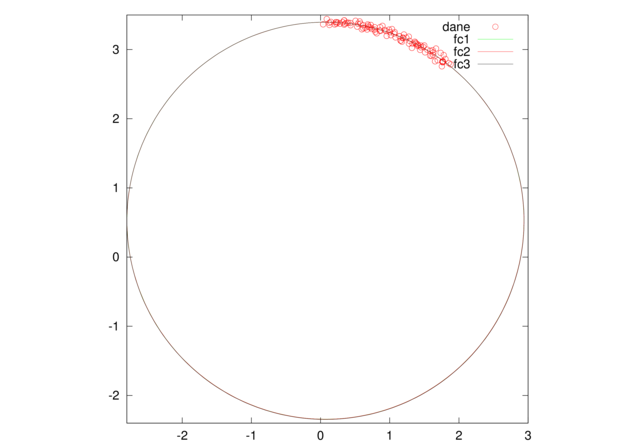
Poniżej przytaczamy przykładowy skrypt dopasowujący okrąg do zadanych punktów trzema opisanymi wcześniej metodami.
t = linspace(0,0.2*pi,100)';
X = 3*sin(t)+0.2*rand(size(t));
Y = 3.35*cos(t)+0.1*rand(size(t));
XY = [X,Y];
e = fitcircle3(X,Y);
c = fitcircle1(e,X,Y);
d = fitcircle2(e,X,Y);
[e c d]
t = linspace(0,2*pi,300);
plot(X,Y,'ro');
axis('square');
hold on;
plot(c(1) + c(3)*sin(t),c(2)+c(3)*cos(t),'g-');
plot(d(1) + d(3)*sin(t),d(2)+d(3)*cos(t),'r-');
plot(e(1) + e(3)*sin(t),e(2)+e(3)*cos(t),'k-');
plot(X,Y,'ro');
hold off;
legend('dane', 'fc1', 'fc2', 'fc3');
[residgeom(c,X,Y), residgeom(d,X,Y), residgeom(e,X,Y)]