Zagadnienia

4.1 Równanie Michaelisa–Menten
- 4.1.1 Nietrafione uproszczenia
- 4.1.2 Rozwiązanie nieliniowego zadania najmniejszych kwadratów
4.2 Różniczkowy model łańcucha reakcji enzymatycznych

4. Reakcja enzymatyczna

4.1. Równanie Michaelisa–Menten

W jednym z prostszych modeli reakcji enzymatycznych pojawia się równanie Michaelisa–Menten, ustanawiające zależność szybkość reakcji $v_{0}$ od stężenia substratu $S$ :

$v_{0}=\dfrac{V\, S}{K_{m}+S}.$

(4.1)

Współczynniki $K_{m}$ i $V$ są pewnymi parametrami ( $K_{m}$ nazywa się stałą Michaelisa) — por. także wykład z Modeli matematycznych w biologii i medycynie. Wartości $v_{0}$ i $S$ można zmierzyć doświadczalnie, [32] (zob. także [13]) podaje m.in. następujący zestaw danych:

$S\quad[\text{mmol}\,\text{dm}^{{-3}}]$	0.25	0.30	0.40	0.50	0.70	1.00	1.40	2.00
$v_{0}\quad[\text{$\mu{}$mol}\,\text{dm}^{{-3}}\,\text{min}^{{-1}}]$	2.4	2.6	4.2	3.8	6.2	7.4	10.2	11.4

Naszym zadaniem jest wyznaczenie takich wartości parametrów $K_{m}$ i $V$ , które najlepiej pasowałyby do powyższych danych eksperymentalnych.

4.1.1. Nietrafione uproszczenia

Wielu badaczy, jeszcze w czasach gdy obliczenia były zaporowo drogie, zaproponowało rozmaite transformacje powyższego problemu, pozwalające w ostatecznym rozrachunku sformułować zadanie jako liniowe zadanie najmniejszych kwadratów. Mając w pamięci numeryczną maksymę, że

Jeśli zadanie jest za trudne, należy… zmienić zadanie!

możemy ulec wrażeniu, że będzie to właściwa droga ku efektywnemu znalezieniu ,,optymalnych” wartości szukanych parametrów.

W przypadku zadania dopasowania $K_{m}$ i $V$ , używano (por. [10]) między innymi takich (matematycznie równoważnych) transformacji (4.1):

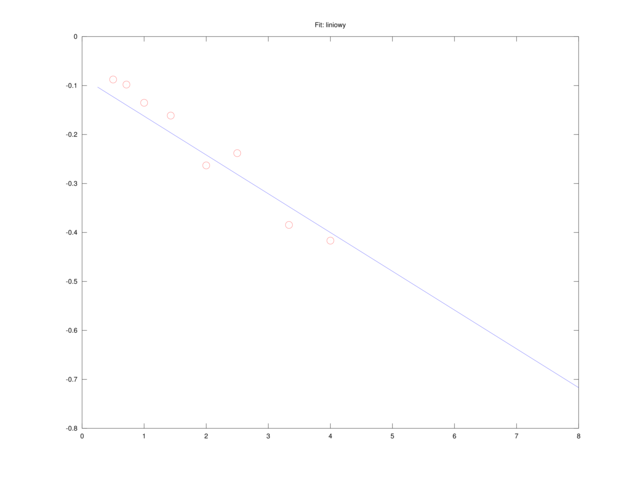
Równanie czysto liniowe

Mnożąc (4.1) stronami przez $K_{m}+S$ i dzieląc przez $S$ , dostajemy równanie liniowe względem $K_{m}$ i $V$ :

$K_{m}\dfrac{1}{S}-V\dfrac{1}{v_{0}}=-1,$

(4.2)

które możemy oczywiście rozwiązać metodą najmniejszych kwadratów. Jeśli wektory kolumnowe S i v0 będą zawierać dane z pomiarów (odpowiednio: $S_{i}$ i $(v_{0})_{i}$ , $i=1,\ldots,N$ ), to instrukcje

e = ones(size(S),1);

A = [1./S, -1./v0]; b = -e;
x = A \ b;

V = x(2); Km = x(1);

spowodują wyznaczenie $K_{m}$ i $V$ takich, które zminimalizują sumę

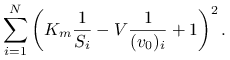$\sum _{{i=1}}^{N}\left(K_{m}\dfrac{1}{S_{i}}-V\dfrac{1}{(v_{0})_{i}}+1\right)^{2}.$

Rys. 4.1. Dopasowanie prostej do danych w równaniu liniowym (4.2).

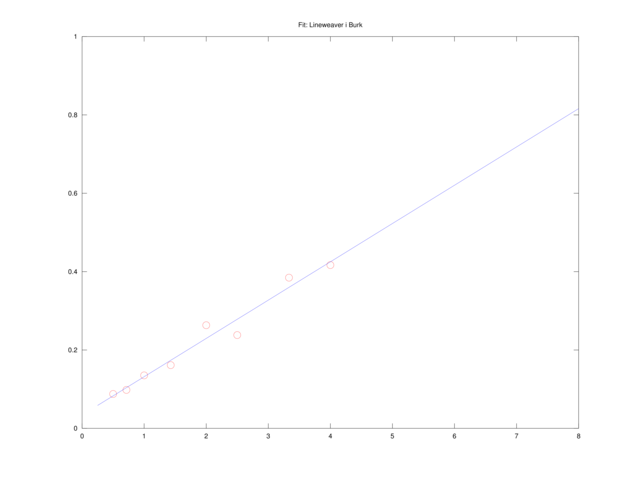
Równanie Lineweavera i Burka

Jeśli poprzednio wyprowadzone równanie podzielimy przez $V$ , dostaniemy równanie Lineweavera i Burka,

$\dfrac{1}{v_{0}}=\dfrac{1}{V}+\dfrac{K_{m}}{V}\dfrac{1}{S}=x_{2}+x_{1}\dfrac{1}{S},$

które jest liniowe względem pomocniczych zmiennych $x_{1}=\dfrac{K_{m}}{V}$ , $x_{2}=\dfrac{1}{V}$ .

Analogicznie jak poprzednio, możemy znaleźć wartości $x_{1},x_{2}$ , które zminimalizują wyrażenie

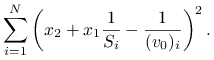$\sum _{{i=1}}^{N}\left(x_{2}+x_{1}\dfrac{1}{S_{i}}-\dfrac{1}{(v_{0})_{i}}\right)^{2}.$

Rozwiążemy je w Octave, korzystając z operatora ,,\”, sekwencją komend:

A = [1./S, e]; b = 1./v0;
x = A \ b;
V = 1/x(2); Km = x(1)*V;

Fit jest w miarę niezły, ale dane punkty zagęszczają się przy S bliskich zero!

Rys. 4.2. Dopasowanie prostej do danych w równaniu Lineweavera i Burka.

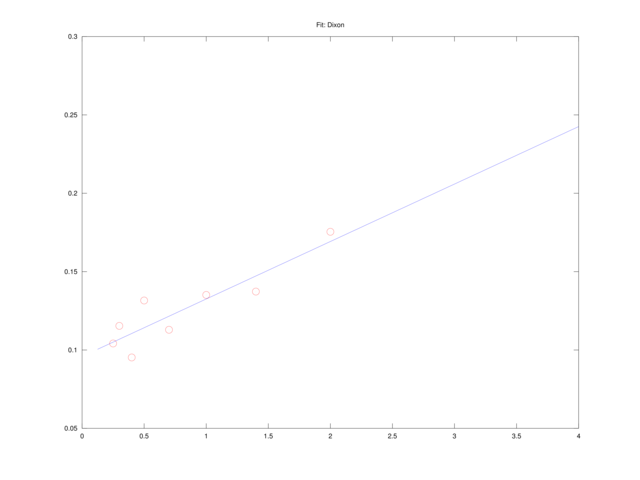
Równanie Dixona

Mnożąc równanie Lineweavera i Burka przez $S$ , dostajemy równanie Dixona,

$\dfrac{S}{v_{0}}=\dfrac{1}{V}S+\dfrac{K_{m}}{V}=x_{2}S+x_{1},$

liniowe w pomocniczych zmiennych $x_{1}=\dfrac{K_{m}}{V}$ , $x_{2}=\dfrac{1}{V}$ . Ponownie więc możemy dopasować $K_{m}$ i $V$ , rozwiązując liniowe zadanie najmniejszych kwadratów.

Zadane punkty nie wyglądają na ułożone wzdłuż prostej!

Rys. 4.3. Dopasowanie prostej do danych w równaniu Dixona.

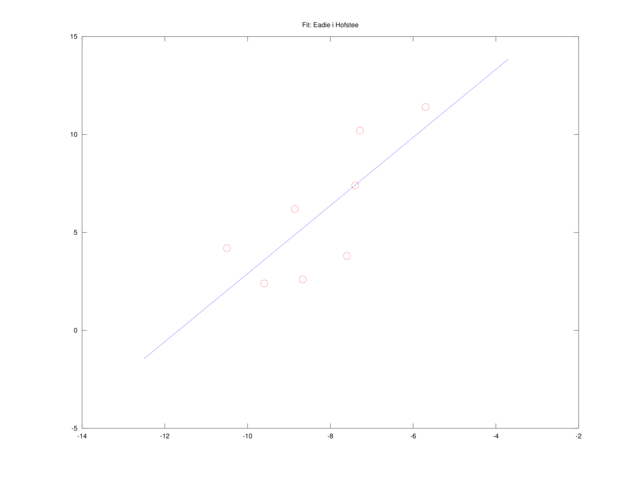
Równanie Eadie i Hofstee

Mnożąc wreszcie równanie liniowe (4.2) przez $v_{0}$ , dochodzimy do równania postaci:

$-K_{m}\dfrac{v_{0}}{S}+V=v_{0},$

które jest liniowe w oryginalnych zmiennych, $K_{m}$ i $V$ . To zadanie też możemy rozwiązać przez liniowe zadanie najmniejszych kwadratów.

Rys. 4.4. Dopasowanie prostej do danych w równaniu Eadie i Hofstee.

Ćwiczenie 4.1

Dla danych podanych w tabeli na początku rozdziału, wyznacz każdym z opisanych sposobów współczynniki $K_{m}$ i $V$ .

Rozwiązanie:

Przykładowe rozwiązania znajdują się w listingu w dalszej części wykładu. Swoją odpowiedź możesz porównać z tabelką w następnym rozdziale.

4.1.1.1. Krytyka metod prowadzących do liniowego zadania najmniejszych kwadratów

Powstaje więc — bynajmniej nie filozoficzne, ale czysto praktyczne — pytanie, która z metod jest ,,lepsza”, czyli która z nich da najlepsze możliwe dopasowanie (przy rozsądnym koszcie). Otóż wszystko zależy od tego, co będziemy rozumieli pod pojęciem ,,najlepsze”: wszak z definicji każde z uzyskanych przez nas rozwiązań było najlepsze, jako rozwiązanie zadania minimalizacji residuum postaci $\| b-Ax\| _{2}^{2}$ dla zadanych $A$ i $b$ .

Ponieważ ,,naturalnym” sformułowaniem naszego zadania było (4.1), wydaje się równie naturalnym postawienie i ocena rozwiązania w sensie nieliniowego zadania najmniejszych kwadratów:

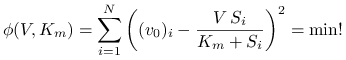$\phi(V,K_{m})=\sum _{{i=1}}^{N}\left((v_{0})_{i}-\dfrac{V\, S_{i}}{K_{m}+S_{i}}\right)^{2}=\min!$

(4.3)

Jeśli porównać wartości $\phi$ dla parametrów otrzymanych wyżej opisanymi metodami, to okaże się, że

równanie	$V$	$K_{m}$	$\phi(V,K_{m})$	uwarunkowanie ( $\kappa$ )
Lineweaver i Burk	29.43	2.88	1.71	12.1
Dixon	27.27	2.61	1.58	7.13
Eadie i Hofstee	20.27	1.74	2.65	874
liniowe	12.00	0.95	23.40	3170

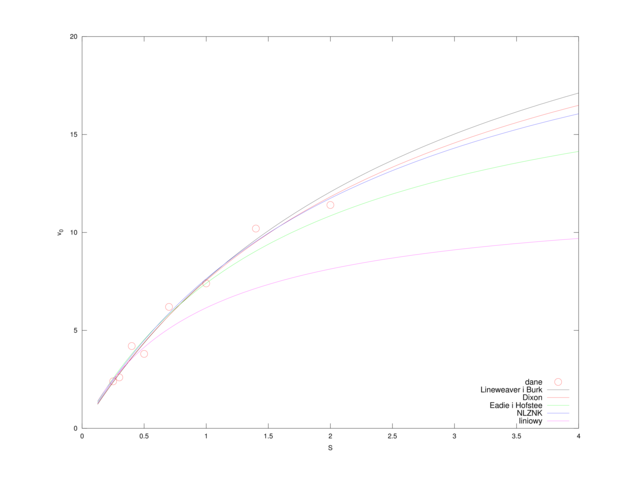
A więc w tym sensie, zdecydowanie najlepsze rezultaty dało dopasowanie metodą Dixona (por. także rysunek 4.5). Co więcej, okazuje się, że metody prowadzące do liniowej zależności od $V$ i $K_{m}$ , czyli równanie liniowe (4.2) i równanie Eadie i Hofstee są bardzo źle uwarunkowane¹⁰Współczynnik uwarunkowania zadania odzwierciedla podatność wyniku na zaburzenia danych. Gdy zadanie jest źle uwarunkowane (tzn. ma bardzo duży współczynnik uwarunkowania), nawet małe zaburzenie danych może spowodować bardzo duży błąd wyniku., ze współczynnikiem uwarunkowania $\kappa$ rzędu $10^{3}$ . Jest to o tyle ważne, że dane do naszego zadania zdają się być zmierzone z dokładnością względną $\epsilon$ rzędu $10^{{-1}}\ldots 10^{{-2}}$ : taki błąd może więc skutkować zaburzeniem względnym wyniku na poziomie rzędu $\kappa\epsilon$ , czyli na poziomie $10^{1}\ldots 10^{2}$ .

Sensowne wyniki dają metody Lineweaver i Burk oraz Dixona, ale… czy nie można jeszcze lepiej? Wszak możemy spróbować rozwiązać wprost nieliniowe zadanie najmniejszych kwadratów (4.3), na przykład korzystając z solvera sqp, dostępnego w Octave.

4.1.2. Rozwiązanie nieliniowego zadania najmniejszych kwadratów

Solversqp jest narzędziem służącym do rozwiązywania znacznie bardziej złożonych zadań optymalizacji, dlatego jego użycie bywa skomplikowane. Ale w naszym prostym przypadku — minimalizacji bez ograniczneń, dla funkcjonału kwadratowego — nie będziemy musieli podawać mu zbyt wielu parametrów. Najpierw jednak zdefiniujemy funkcjonał, który będziemy minimalizować:

% (X(1), X(2)) <---> (V, K)
F = @(X,S) (X(1)*S)./(X(2)+S);
phi = @(X) sumsq(v0 - F(X,S));

Jak widać, zaczęliśmy od określenia funkcji

$F_{{V,K_{m}}}(S)=\dfrac{V\, S}{K_{m}+S},$

która pojawia się w definicji (4.1) i w (4.3), i która z pewnością nam się przyda: na przykład do narysowania wykresu $F$ dla wyznaczonych $V$ i $K_{m}$ (dlatego definiujemy ją od razu wektorowo ze względu na $S$ ). Potem, przy użyciu $F$ , zdefiniowaliśmy $\phi$ , przy czym — ponieważ phi jest anonimową funkcją tylko jednego argumentu, X, to w jej definicji zostaną użyte wcześniej przez nas zdefiniowane wektory S i v0, zawierające dane zadania. Dzięki temu, łatwo nam będzie wyznaczyć sumę kwadratów współrzędnych wektora v0 - F(X,S) — do tego właśnie służy funkcja Octave sumsq.

Teraz wystarczy wywołać solver sqp na naszym funkcjonale $\phi$ , z początkowym przybliżeniem $(V,K_{m})^{T}$ wyznaczonym np. metodą Dixona:

% podane na wejściu sqp parametry (V, Km) zostały wyznaczone metodą Dixona
[x, phix, info, iter, nphi] = sqp([V;Km], phi)
V = x(1); Km = x(2);

W wyniku dostajemy $V=25.40$ oraz $K_{m}=2.33$ , dla których $\phi(V,K_{m})=1.51$ , a więc (nieco) lepiej niż dotychczas! Jak zwykle w przypadku metod iteracyjnych, zażądamy możliwie wielu informacji diagnostycznych, takich jak: kod zakończenia info, liczba wykonanych iteracji iter, oraz wywołań funkcjonału nphi. Pożądana wartość info to, zgodnie z manualem, 101: zakończenie z powodu nikłego postępu iteracji. Musimy jednak pamiętać, że znalezione minimum może być jedynie minimum lokalnym i wybór innego punktu startowego może dać w rezultacie znacznie lepszy (lub gorszy) wynik.

Podsumowując, w dzisiejszych czasach, gdy nawet dość zaawansowae obliczenia są (w miarę) łatwe i tanie, nie powinniśmy bać się nieliniowości. Pamiętajmy także, że jeśli tylko możemy sensownie wspomóc się przybliżeniem uzyskanym na drodze rozsądnej linearyzacji — warto z tej opcji skorzystać.

Na marginesie dodajmy, że opisane przez nas wcześniej metody sprowadzenia zadania do zadania liniowego, są wciąż rutynowo stosowane w innych zadaniach dopasowywania do punktów pomiarowych wykresu, na przykład postaci $y(x)=ae^{{bx}}$ : biorąc logarytm od obu stron, ponownie dostajemy zadanie liniowe na $a$ i $b$ : $\log(y)=\log(a)+bx$ . Jednak, jak już doświadczyliśmy, transformacja zadania najczęściej powoduje też zmianę sposobu, w jaki mierzymy błąd dopasowania. Niektóre transformacje dodatkowo mogą wyolbrzymiać lub redukować różnice pomiędzy danymi punktami pomiarowymi.

$Naprawdę, tylko fit nieliniowy oraz fit Dixona są zadowalające; jednak \emph{ekstrapolacja} obu daje już wyraźnie różne rezultaty! Fity oparte na sprowadzeniu zadania do prostego zadania liniowego okazały się najgorsze.$

Rys. 4.5. Dopasowanie krzywej (4.1) do danych dla różnych sposobów wyznaczenia parametrów.

S = [0.25 ; 0.30; 0.40; 0.50; 0.70; 1.00; 1.40; 2.00];
v0 = [2.4; 2.6; 4.2; 3.8; 6.2; 7.4; 10.2; 11.4];

F = @(X,S) (X(1)*S)./(X(2)+S);
fitfun = @(X) sumsq(v0 - F(X,S));

function cbA = lsqcond(A, b, x, tol)
if nargin < 4
	tol = 1e2;
end
c = norm(A*x)/norm(b);
t = norm(A*x-b)/norm(A*x);
condA = cond(A);
cb = condA/c;
cA = (condA^2)*t + condA;
cbA = cb+cA;
if (cbA) > tol
	warning(['Uwarunkowanie zadania: ', num2str([cb, cA])]);
end
end

p = 0; n = 100;
s = linspace(0.125,4,n);

e = ones(size(S));

model = 5;
A = [1./S, -1./v0]; b = -e;
x = A \ b;
V(model) = x(2); Km(model) = x(1);
resid(model) = fitfun([V(model),Km(model)]);
cbA(model) = lsqcond(A,b,x);
plot(A(:,1), A(:,2), 'ro'); hold on;
plot(1./s, -(1+x(1)./s)/x(2),'-b'); hold off;
title('Fit: liniowy'); pause(p);
print('-depsc','linear.eps');

% Lineweaver i Burk
model = 1;
A = [1./S, e]; b = 1./v0;
x = A \ b;
V(model) = 1/x(2); Km(model) = x(1)*V(model);
resid(model) = fitfun([V(model),Km(model)]);
cbA(model) = lsqcond(A,b,x);
plot(A(:,1), b, 'ro'); hold on;
plot(1./s, x(1)./s+x(2),'-b'); hold off;
title('Fit: Lineweaver i Burk'); pause(p);
print('-depsc','lib.eps');

% Dixon
model = 2;
A = [e, S]; b = S./v0;
x = A \ b;
V(model) = 1/x(2); Km(model) = x(1)*V(model); 
resid(model) = fitfun([V(model),Km(model)]);
cbA(model) = lsqcond(A,b,x);
plot(A(:,2), b, 'ro'); hold on;
plot(s, x(2)*s+x(1),'-b'); hold off;
title('Fit: Dixon'); pause(p);
print('-depsc','dixon.eps');


% Eadie i Hofstee
model = 3;
A = [-v0./S, e]; b = v0;
x = A \ b;
V(model) = x(2); Km(model) = x(1);
resid(model) = fitfun([V(model),Km(model)]);
cbA(model) = lsqcond(A,b,x);
plot(A(:,1), b, 'ro'); hold on;
s3 = linspace(min(A(:,1))-2, max(A(:,1))+2, 100);
plot(s3, x(1)*s3+x(2),'-b'); hold off;
title('Fit: Eadie i Hofstee'); pause(p);
print('-depsc','eih.eps');

% nonlinear fit; X = (V,Km)
model = 4;
[x, fitfunx, info, iter, nF, lambda] = sqp([V(2);Km(2)], fitfun);
V(model) = x(1); Km(model) = x(2); 
resid(model) = fitfun([V(model),Km(model)]);
cbA(model) = NA;
if info ~= 101
	warning('SQP: problemy z rozwiazaniem zadania');
end

printf('+------+---------+--------+----------+----------+\n');
printf(' Model | V       | K      | resid    | cond\n');
printf('+------+---------+--------+----------+----------+\n');
printf(' %2d    | %4.2f   | %4.2f   | %6.2f   | %4.2e\n', [1:length(V);V;Km;resid;cbA]);
printf('+------+---------+--------+----------+----------+\n');

plotname = {'dane','Lineweaver i Burk','Dixon','Eadie i Hofstee','NLZNK','liniowy'};
plot(S, v0, 'ro');
hold on;
for i = 1:length(V)
	plot(s, F([V(i),Km(i)],s) , ['-', num2str(i-1)]);
	pause(p);
end
hold off;
xlabel('S'); ylabel('v_0');
legend(plotname, 'location', 'southeast');
print('-depsc','michaelis-fit.eps')

4.2. Różniczkowy model łańcucha reakcji enzymatycznych

W rozdziale 6. pracy [24] rozważa się model łańcucha trzech reakcji katalizowanych enzymatycznie. Niech $X_{7}$ oznacza (dane) stężenie substratu, $X_{2}$ i $X_{4}$ — (niewiadome) stężenie dwóch produktów pośrednich, a $X_{6}$ — (dane) stężenie produktu finalnego reakcji. Dalej, niech $X_{8},X_{9},X_{{10}}$ będą zadanymi całkowitymi stężeniami trzech enzymów katalizujących każdą z reakcji (zob. rysunek 4.6 pochodzący z (Źródło: [24, rysunek 9]), przy czym $X_{1},X_{3},X_{{5}}$ będą nieznanymi stężeniami odpowiednich enzymów związanych z produktami pośrednimi (a przez to nieczynnymi). Stężenia wolnych enzymów oznaczymy przez $X_{{11}}=X_{8}-X_{1}$ , $X_{{12}}=X_{9}-X_{3}$ , $X_{{13}}=X_{{10}}-X_{5}$ .

X7, z pomocą enzymu X1 przechodzi w X2, a ten, z pomocą enzymu X3 przechodzi w X4, który to katalizowany enzymem X5 przemienia się w produkt finalny X6. Wolne enzymy są reprezentowane przez X11, X12, X13.

Rys. 4.6. Schematyczne przedstawienie omawianej reakcji enzymatycznej.

Wtedy kinetyka powyższego układu może być modelowana następującym zestawem równań różniczkowych zwyczajnych [24, równania (75)—(82)]¹¹Podajemy go już po pewnych uproszczeniach.:

	$\displaystyle\dfrac{d}{dt}X_{1}$	$\displaystyle=aX_{7}^{c}X_{{11}}^{c}+bX_{2}^{c}X_{{11}}^{c}-(b+a)X_{1},$
	$\displaystyle\dfrac{d}{dt}X_{2}$	$\displaystyle=aX_{1}+bX_{3}-bX_{2}^{c}X_{{11}}^{c}-aX_{2}^{c}X_{{12}}^{c},$
	$\displaystyle\dfrac{d}{dt}X_{3}$	$\displaystyle=aX_{2}^{c}X_{{12}}^{c}+bX_{4}^{c}X_{{12}}^{c}-(b+a)X_{3},$
	$\displaystyle\dfrac{d}{dt}X_{4}$	$\displaystyle=aX_{3}+bX_{5}-bX_{4}^{c}X_{{12}}^{c}-aX_{4}^{c}X_{{13}}^{c},$
	$\displaystyle\dfrac{d}{dt}X_{5}$	$\displaystyle=aX_{4}^{c}X_{{13}}^{c}+bX_{6}^{c}X_{{13}}^{c}-(b+a)X_{5},$

z parametrami $a,b,c$ , uzupełnionego warunkiem początkowym dla $t=0$ . Naszym zadaniem jest wyznaczenie wykresu zależności prędkości (netto) $v$ powstawania produktu od czasu $t$ , zgodnie ze wzorem [24, równanie (83)]

$v(t)=aX_{5}-bX_{6}^{c}(X_{{10}}-X_{5})^{c}.$

W tym celu w rutynowy sposób wyznaczymy rozwiązanie powyższego układu równań, korzystając z funkcji lsode. Najpierw jednak zapiszemy układ równań w formie takiej, by występowały w nim jedynie niewiadome $X_{1},\ldots,X_{5}$ oraz zadane parametry $X_{6},\ldots,X_{{10}}$ :

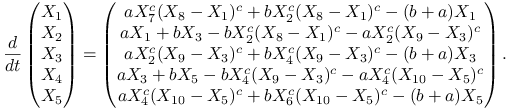$\displaystyle\dfrac{d}{dt}\begin{pmatrix}X_{1}\\ X_{2}\\ X_{3}\\ X_{4}\\ X_{5}\end{pmatrix}=\begin{pmatrix}aX_{7}^{c}(X_{8}-X_{1})^{c}+bX_{2}^{c}(X_{8}-X_{1})^{c}-(b+a)X_{1}\\ aX_{1}+bX_{3}-bX_{2}^{c}(X_{8}-X_{1})^{c}-aX_{2}^{c}(X_{9}-X_{3})^{c}\\ aX_{2}^{c}(X_{9}-X_{3})^{c}+bX_{4}^{c}(X_{9}-X_{3})^{c}-(b+a)X_{3}\\ aX_{3}+bX_{5}-bX_{4}^{c}(X_{9}-X_{3})^{c}-aX_{4}^{c}(X_{{10}}-X_{5})^{c}\\ aX_{4}^{c}(X_{{10}}-X_{5})^{c}+bX_{6}^{c}(X_{{10}}-X_{5})^{c}-(b+a)X_{5}\end{pmatrix}.$

W naszych eksperymentach numerycznych przyjmiemy za [24] $a=2$ , $b=1$ , $c=4$ , a także $X_{8}=X_{9}=X_{{10}}=1$ . Ponadto $X_{7}=1.425$ (badając model tak, jak w [24], sprawdzalibyśmy wpływ zmiany tego parametru na zmianę $v$ ), $X_{6}=1$ . W chwili $t=0$ , ustalamy $X_{1}(0)=\ldots=X_{5}(0)=0$ . Oczywiście, cały skrypt symulujący przebieg reakcji zapiszemy w formie sparametryzowanej tak, by móc łatwo zmieniać wartości wszystkich danych zadania.

Funkcja prawej strony miałaby więc postać¹²Jeżeli w definicji dX przypadkowo napiszesz dX = [ a -b; ..itd..], to interpreter Octave zrozumie, że chodzi o macierz o dwóch kolumnach, dX = [ a, -b; ..itd..]. Dlatego, powinniśmy tutaj konsekwentnie pisać dX = [ a - b; ..itd..] (z operatorem odejmowania otoczonym spacjami).

function dX = reaction(X,t)
global a;
global b;
global c;
global X6;
global X7;
global X8;
global X9;
global X10;

dX = [a*(X7*(X8-X(1)))^c + b*(X(2)*(X8-X(1)))^c - (b+a)*X(1) ;
a*X(1) + b*X(3) - b*(X(2)*(X8-X(1)))^c - a*(X(2)*(X9-X(3)))^c ;
a*(X(2)*(X9-X(3)))^c + b*(X(4)*(X9-X(3)))^c - (b+a)*X(3) ;
a*X(3) + b*X(5) - b*(X(4)*(X9-X(3)))^c - a*(X(4)*(X10-X(5)))^c ;
a*(X(4)*(X10-X(5)))^c + b*(X6*(X10-X(5)))^c - (b+a)*X(5)];
end

(dla większej skuteczności iloczyny postaci $X^{c}Y^{c}$ zapisaliśmy $(XY)^{c}$ ). Natomiast skrypt symulacji mógłby wyglądać na przykład następująco:

global a;
global b;
global c;
global X6;
global X7;
global X8;
global X9;
global X10;

a = 2; b = 1; c = 4;
X6 = X8 = X9 = X10 = 1;
X7 = 1.425;
T = 10;

N = 800;
t = linspace(0,T,N);
X = lsode(@reaction, zeros(5,1), t);
plot(t,X); pause(3);
v = a*X(:,5) - b*(X6*(X10-X(:,5))).^c;
plot(t,v)

Tradycyjnie, aby nieco upewnić się co do jakości otrzymanych wyników, powinniśmy przeprowadzić kilka symulacji z różnymi parametrami tolerancji błędu (i zbadać, czy przypadkiem nie padliśmy ofiarą aliasingu, czyli zbyt małej rozdzielczości wizualizacji, fałszującej rzeczywisty przebieg rozwiązania).

Ćwiczenie 4.2

Przeprowadź testy wizualnej i numerycznej jakości uzyskanego rozwiązania, zmieniając N (by zabezpieczyć się przed aliasingiem) oraz lsode_options (by zmniejszyć ryzyko wzięcia numerycznych artefaktów za prawdziwe własności rozwiązania).

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Obliczenia naukowe