1. Wiadomości wstępne
1.1. Wprowadzenie
Rozpoczniemy od przedstawienia kilku charakterystycznych przykładów zadań optymalizacji liniowej.
Zagadnienie diety.
Jak wymieszać pszenicę, soję i mączkę rybna by uzyskać najtańszą mieszankę zapewniającą wystarczającą zawartość węglowodanów, białka i soli mineralnych dla kurcząt.
Zapotrzebowanie, zawartość składników i ceny przedstawia następująca tabela:
![\begin{array}[]{|c|c|c|c|c|}\hline&\text{węglowodany}&\text{białko}&\text{sole mineralne}&\text{cena}\\
\cline{1-5}\text{pszenica}&0,8&0,01&0,15&300~\text{zł/t}\\
\text{soja}&0,3&0,4&0,1&500~\text{zł/t}\\
\text{mączka}&0,1&0,7&0,2&800~\text{zł/t}\\
\hline\text{zapotrzebowanie}&0,3&0,7&0,1&\\
\hline\end{array}](wyklady/op1/mi/mi60.png)
Rozpoczynamy od zdefiniowania zmiennych. Niech ![]() oznacza wagę i-tego składnika w mieszance.
oznacza wagę i-tego składnika w mieszance.
Funkcją celu jest
![]() - czyli koszt mieszanki.
- czyli koszt mieszanki.
Ograniczenia są dwojakiego typu
a) W mieszance musi być wystarczająco każdego ze składników:
![]()
![]()
![]()
b) Waga używanych składników jest nieujemna.
![]()
Podsumowując. Szukamy najmniejszej wartości funkcji trzech zmiennych ![]() ograniczonej do podzbioru
ograniczonej do podzbioru ![]() zwanego obszarem dopuszczalnym.
zwanego obszarem dopuszczalnym.
Zadanie to nazywamy liniowym, bo funkcja celu ![]() zależy
liniowo od zmiennych
zależy
liniowo od zmiennych ![]() i obszar dopuszczalny
opisany jest zbiorem nierówności liniowych.
i obszar dopuszczalny
opisany jest zbiorem nierówności liniowych.
Zagadnienie transportowe:
Mamy 3 hurtownie i 5 sklepów. Koszt transportu jednostki towaru
z ![]() - tej hurtowni do
- tej hurtowni do ![]() - tego sklepu przedstawia tabela.
- tego sklepu przedstawia tabela.
![\begin{array}[]{|c|ccccc|c|}\hline Koszt&S_{1}&S_{2}&S_{3}&S_{4}&S_{5}&\text{podaż}\\
\hline H_{1}&8&12&15&13&21&10\\
H_{2}&0&1&8&3&4&31\\
H_{3}&5&8&7&8&6&20\\
\hline\text{popyt}&10&10&20&10&11&\\
\hline\end{array}](wyklady/op1/mi/mi1622.png)
Jak zorganizować transport, żeby koszt całkowity był minimalny?
Wprowadźmy zmienne ![]() opisujące ilość towaru przewożonego z
opisujące ilość towaru przewożonego z
![]() - tej hurtowni do
- tej hurtowni do ![]() - tego sklepu.
- tego sklepu.
Niech ![]() oznacza koszt przewiezienia jednostki towaru przewożonego z
oznacza koszt przewiezienia jednostki towaru przewożonego z
![]() - tej hurtowni do
- tej hurtowni do ![]() - tego sklepu.
- tego sklepu.
Jako funkcję celu przyjmijmy: ![]()
Rozpatrzmy przypadek gdy zadanie jest zbilansowane, czyli gdy podaż = popyt.
Wtedy warunkami ograniczającymi są:
Aby pierwsza hurtownia wysłała cały towar to: ![]()
analogicznie dla pozostałych hurtowni:
![]()
Aby pierwszy sklep otrzymał cały zamówiony towar towar to: ![]() ,
,
analogicznie dla pozostałych sklepów
![]() ,
,
![]() .
.
Ponadto nie można przewozić ujemnej liczby towarów - a więc:
![]()
Czasami towary są podzielne jak prąd czy woda, ale często dodajemy warunek, że zmienne są liczbami całkowitymi - czyli dodajemy warunki:
![]() .
.
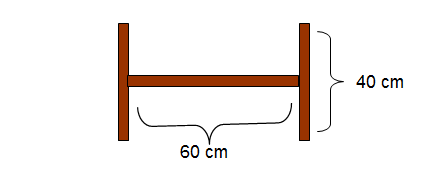
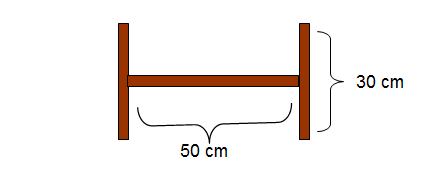
Dylemat stolarza
Stolarz ma zamówienie na 11 półek o kształcie jak na rysunku:
Ile desek o długości 220 cm potrzebuje na wykonanie zamówienia?
Na początku ustalamy sposoby cięcia desek:
![\begin{array}[]{|c|c|c|}\hline i&60\, cm&40\, cm\\
\hline 1&3&1\\
2&2&2\\
3&1&4\\
4&0&5\\
\hline\end{array}](wyklady/op1/mi/mi84.png)
Wprowadzamy zmienne: ![]() - liczba desek ciętych i-tym
sposobem.
- liczba desek ciętych i-tym
sposobem.
Teraz matematyczny model zagadnienia wygląda następująco:
![]()
![]()
![]()
![]() ,
, ![]()
Zadania tego typu występują często w realnym życiu gdyż huty dostarczają do fabryk pręty określonej długości, które trzeba oszczędnie pociąć lub taśmę, z której trzeba wykroić detale.
Jak widzimy w zadaniach optymalizacji liniowej opisujące obszar dopuszczalny są równaniami lub nierównościami liniowymi. Do pewnego stopnia te typy warunków są wymienne.
Równość ![]() można zastąpić układem nierówności.
można zastąpić układem nierówności.
![]()
lub równoważnie:
![]()
Podobnie nierówność ![]()
można zastąpić układem:
![]()
Podobnie warunki minimum i maksimum w funkcji celu można stosować
wymiennie gdyż:
![]()
1.2. Zbiory wypukłe i zbiory domknięte
Zagadnienie optymalizacji polega na znalezieniu minimum lub maksimum funkcji ![]() , gdzie
, gdzie ![]() jest podzbiorem
jest podzbiorem ![]() zwanym obszarem dopuszczalnym. Od zbioru
zwanym obszarem dopuszczalnym. Od zbioru ![]() wymagamy by był domknięty i wypukły.
wymagamy by był domknięty i wypukły.
Zaczniemy od opisania najważniejszych własności zbiorów wypukłych i domkniętych.
Definicja 1.1
Podzbiór ![]() nazywamy domkniętym jeżeli granica każdego zbieżnego ciągu punktów z
nazywamy domkniętym jeżeli granica każdego zbieżnego ciągu punktów z ![]() należy do zbioru
należy do zbioru ![]() . Lub równoważnie: Jeżeli punkt
. Lub równoważnie: Jeżeli punkt ![]() nie należy do
nie należy do ![]() to istnieje
to istnieje ![]() taki, że kula o środku p i promieniu
taki, że kula o środku p i promieniu ![]() jest rozłączna z
jest rozłączna z ![]() . Symbolami zapisujemy to:
. Symbolami zapisujemy to: ![]() .
.
Będziemy też używać znanego twierdzenia o zbiorach domkniętych.
Twierdzenie 1.1
Część wspólna zbiorów domkniętych jest zbiorem domkniętym.
Definicja 1.2
Domknięciem zbioru ![]() nazywamy zbiór
nazywamy zbiór
![]() domknięty
domknięty![]()
czyli najmniejszy zbiór domknięty zawierający ![]() .
.
Jedną z najważniejszych własności obszaru dopuszczalnego jest wypukłość.
Definicja 1.3
Wypukłość
Podzbiór ![]() jest wypukły jeśli wraz z każdymi dwoma
punktami zawiera odcinek łączący je, czyli:
jest wypukły jeśli wraz z każdymi dwoma
punktami zawiera odcinek łączący je, czyli:
![]()
![]()
Odcinek ![]() możemy zapisać jako
możemy zapisać jako
![]() .
.
Ostatni zapis czytamy: ![]() jest zbiorem
kombinacji wypukłych punktów
jest zbiorem
kombinacji wypukłych punktów ![]() i
i ![]() .
.
Definicja 1.4
Brzegiem zbioru![]() nazywamy zbiór
nazywamy zbiór
![]() .
.
Twierdzenie 1.2
Podzbiór ![]() jest domknięty wtedy i tylko wtedy gdy zawiera swój brzeg, czyli:
jest domknięty wtedy i tylko wtedy gdy zawiera swój brzeg, czyli:
![]() .
.
![]() Niech
Niech ![]() . Wtedy istnieje
. Wtedy istnieje ![]() taki, że
taki, że ![]() . Stąd
. Stąd ![]() .
.
![]() Niech
Niech ![]() . Ponieważ
. Ponieważ ![]() więc istnieje
więc istnieje ![]() taki, że
taki, że ![]() . Stąd
. Stąd ![]() .
.
Definicja 1.5
Półprzestrzenią w ![]() nazywamy zbiór rozwiązań nietrywialnej
nierówności liniowej, a zatem zbiór postaci:
nazywamy zbiór rozwiązań nietrywialnej
nierówności liniowej, a zatem zbiór postaci:
![]()
Twierdzenie 1.3
Brzegiem ![]() półprzestrzeni
półprzestrzeni
jest hiperprzestrzeń
Niech ![]() i
i ![]() .
Ponieważ
.
Ponieważ ![]() więc
więc ![]() . Ponadto jeśli
. Ponadto jeśli ![]() i
i ![]() to
to ![]() . Zatem
. Zatem ![]() .
.
Niech teraz ![]() . Wtedy, stosując wzór z algebry liniowej na odległość punktu od hiperprzestrzeni opisanej równaniem, otrzymujemy:
. Wtedy, stosując wzór z algebry liniowej na odległość punktu od hiperprzestrzeni opisanej równaniem, otrzymujemy: ![]() ,
,
więc dla ![]() ,
, ![]() gdy
gdy ![]() i
i ![]() ,
,
gdy ![]() . Stąd
. Stąd ![]() .
.
Twierdzenie 1.4
Półprzestrzeń jest zbiorem wypukłym i domkniętym.
Dowód domkniętości otrzymujemy jako wniosek z dwóch ostatnich twierdzeń.
Dowód wypukłości
Niech ![]() i
i ![]()
Niech ![]() .
.
Pokażemy, że ![]()
![]()
![]()
![]()
Twierdzenie 1.5
Część wspólna zbiorów wypukłych jest zbiorem wypukłym .
Niech ![]() będzie przecięciem zbiorów wypukłych. Weźmy
dwa punkty
będzie przecięciem zbiorów wypukłych. Weźmy
dwa punkty ![]() i
i ![]() ze zbioru
ze zbioru ![]() . Wówczas
. Wówczas ![]() oraz
oraz ![]() . Z wypukłości wynika, że odcinek
. Z wypukłości wynika, że odcinek
![]() . Zatem, wobec dowolności wyboru indeksu
. Zatem, wobec dowolności wyboru indeksu ![]() , odcinek
, odcinek
![]()
Przedstawimy teraz szereg faktów o rozdzielaniu zbiorów domkniętych.
Lemat 1.1
Niech ![]() będzie zbiorem wypukłym i domkniętym i
będzie zbiorem wypukłym i domkniętym i ![]() .
.
Wtedy istnieje taki punkt ![]() , że odległość
, że odległość ![]()
Weźmy dowolny punkt ![]() . Rozpatrujemy
. Rozpatrujemy ![]() . Wtedy
. Wtedy ![]() . Zatem bez zmniejszenia ogólności możemy przyjąć, że zbiór
. Zatem bez zmniejszenia ogólności możemy przyjąć, że zbiór ![]() jest
zwarty.
jest
zwarty.
Niech ![]() ,
, ![]() ,… będzie takim ciągiem punktów
,… będzie takim ciągiem punktów ![]() że
że
![]() .
.
Jeśli ![]() jest zwarty to z
jest zwarty to z ![]() możemy wybrać podciąg
możemy wybrać podciąg ![]() ,
, ![]() , … zbieżny do pewnego punktu
, … zbieżny do pewnego punktu ![]() . Wtedy
. Wtedy ![]() .
.
Twierdzenie 1.6
Jeśli ![]() jest zbiorem wypukłym i domkniętym zaś
jest zbiorem wypukłym i domkniętym zaś ![]() to istnieje
półprzestrzeń
to istnieje
półprzestrzeń ![]() , taka że
, taka że ![]() i
i
![]()
Niech ![]() będzie takim punktem, że
będzie takim punktem, że ![]() .
.
Wiemy, że ![]() , gdzie
, gdzie ![]() oznacza standardowy iloczyn skalarny. Zatem:
oznacza standardowy iloczyn skalarny. Zatem:
![]()
![]()
![]()
analogicznie ![]()
![]()
Przyjmijmy ![]() .
. ![]() jest półpłaszczyzną zawierającą
jest półpłaszczyzną zawierającą ![]() i nie zawierającą
i nie zawierającą ![]() . Jej brzeg
. Jej brzeg ![]() , jak łatwo
policzyć, jest symetralną odcinka
, jak łatwo
policzyć, jest symetralną odcinka ![]() .
.
Przypuśćmy teraz, że istnieje punkt ![]() . Wtedy na odcinku
. Wtedy na odcinku ![]() istnieje punkt
istnieje punkt ![]() . Trójkąt
. Trójkąt ![]() jest równoramienny a ponieważ
jest równoramienny a ponieważ ![]() , z wypukłości, to jego najkrótszym bokiem jest
, z wypukłości, to jego najkrótszym bokiem jest ![]() . Zatem wysokość opuszczona z wierzchołka
. Zatem wysokość opuszczona z wierzchołka ![]() ma spodek
ma spodek ![]() na boku
na boku ![]() . Otrzymaliśmy sprzeczność bo
. Otrzymaliśmy sprzeczność bo ![]() oraz
oraz ![]() . Zatem
. Zatem ![]() .
.
Twierdzenie 1.7
Każdy zbiór wypukły i domknięty w ![]() jest częścią wspólną
półprzestrzeni.
jest częścią wspólną
półprzestrzeni.
Niech ![]() będzie zbiorem wypukłym i domkniętym. Z każdym punktem
będzie zbiorem wypukłym i domkniętym. Z każdym punktem ![]() związujemy pewną półprzestrzeń
półprzestrzeń
związujemy pewną półprzestrzeń
półprzestrzeń ![]() taką, że
taką, że ![]() i
i
![]() . Teraz
. Teraz ![]() .
.
Więcej wiadomości na ten temat można znaleźć w [11].
Zadania
Ćwiczenie 1.3
Opisać wypukłe podzbiory prostej ![]() .
.
Ćwiczenie 1.4
Niech ![]() będzie zbiorem wypukłym w
będzie zbiorem wypukłym w ![]() .
.
a) Pokazać, że
jego domknięcie ![]() też jest zbiorem wypukłym.
też jest zbiorem wypukłym.
b) Pokazać, że
jego wnętrze ![]() też jest zbiorem wypukłym.
też jest zbiorem wypukłym.
Ćwiczenie 1.5
Niech ![]() będzie zbiorem wypukłym w
będzie zbiorem wypukłym w ![]() . Pokazać, że
jeżeli domknięcie
. Pokazać, że
jeżeli domknięcie ![]() to i
to i ![]() .
.