Zagadnienia

5.1 Tablice sympleks
- Zadania
5.2 Metoda sympleks
5.3 Wymiar zbioru punktów optymalnych.
- Zadania

5. Tablice sympleks

5.1. Tablice sympleks

Algorytm sympleks wymaga by obszar dopuszczalny, na którym badamy ekstrema funkcji celu, był wielościanem z wierzchołkiem. Dowolny wielościan możemy ”przerobić” na wielościan z wierzchołkiem przechodząc do zadania równoważnego i zamieniając zmienne tak by były nieujemne.

Jeżeli $x_{i}\leq 0$ to zastępujemy je nową zmienną $x_{i}^{{\prime}}=-x_{i}$ , gdzie $x_{i}^{{\prime}}\geq 0$ .

Jeżeli $x_{i}\in\mathbb{R}$ jest nieograniczone to zastępujemy je różnicą $x_{i}=x_{i}^{+}-x_{i}^{-}$ , gdzie $x_{i}^{+}=\geq 0$ oraz $x_{i}^{-}=\geq 0$ .

W szczególności w tym rozdziale będziemy badać wielościany zapisane w postaci kanonicznej czyli $W=\left\{ x\in R^{{n}}\ |\ Ax^{T}=b,\ x\geq 0\right\}$ .

Opis wierzchołków i krawędzi zadania $PL$ w postaci kanonicznej.

Niech $W=\left\{ x\in R^{{n}}\ |\ Ax^{T}=b,\ x\geq 0\right\}$ będzie wielościanem. Dodatkowo zakładamy, że równania opisujące $W$ są liniowo niezależne - czyli $rzA=t=$ liczba równań.

Niech $p$ będzie wierzchołkiem $W$ . Ze zbioru równań i ”nierówności spełnionych jako równości” które spełnia wierzchołek $p$ wybieramy $n$ liniowo niezależnych w specjalny sposób. Po pierwsze wybieramy $t$ równań $Ax^{T}=b$ opisujących wielościan a potem uzupełniamy do $n$ liniowo niezależnych równań dodając pewne $x_{i}=0$ .

Wynika to z lematu Steinitza o bazie. Dokładniej: ze zbioru równań spełnianych przez $p$ wybieramy dowolnie bazę $\mathcal{A}$ - $n$ liniowo niezależnych równań. Następnie zbiór liniowo niezależny $Ax^{T}=b$ uzupełniamy do bazy równaniami z $\mathcal{A}$ . Muszą to być równania typu $x_{{i_{{1}}}}=0,x_{{i_{{2}}}}=0,...,x_{{i_{{n-t}}}}=0$ Otrzymaliśmy układ $n$ liniowo niezależnych równań z $n$ niewiadomymi, którego jedynym rozwiązaniem jest punkt $p$ . Macierz tego układu oznaczmy literą U.

Zmienne $i_{{1}},...,i_{{n-t}}$ nazywamy niebazowymi zaś pozostałe bazowymi.

Współrzędne niebazowe wierzchołka $p$ są równe $0$ .

Uwaga: Wierzchołek ma co najwyżej $t$ niezerowych współrzędnych.

Dla ułatwienia przenumerujmy tak zmienne by $1,2,...,n-t$ były zmiennymi niebazowymi oraz $n-t+1,...,n$ zmiennymi bazowymi.

Wtedy macierz równania opisującego $W$ składa się z 3 części $A=[N|B|b]$ , gdzie $[B]$ jest macierzą kwadratową.

$rz[U]=n\Rightarrow rzB=t\Rightarrow B$ jest odwracalna.

Mnożąc układ równań $Ax^{T}=b$ z lewej strony przez macierz $B^{{-1}}$ otrzymujemy równoważny opis wielościanu $W$

$\left[B^{{-1}}N|I\right]x^{T}\,=\, B^{{-1}}b=\left[\begin{array}[]{c}b_{{1}}\\ \vdots\\ b_{{t}}\end{array}\right]$

Zaś wierzchołek ma współrzędne $p=(0,...,0,b_{{1}},b_{{2}},...,b_{{t}})$ .

Podsumowując, każdemu wierzchołkowi, przez wybór zmiennych bazowych przyporządkowujemy układ równań o macierzy zawierającej podmacierz jednostkową.

Definicja 5.1

Tablicą sympleks nazywamy taką macierz rozszerzoną układu równań $[A|b]$ , że $A$ zawiera podmacierz jednostkową rozmiaru t. Dokładniej, można z macierzy $A$ tak powykreślać kolumny i poprzestawiać wiersze by uzyskać macierz jednostkową.

Tablicę sympleks nazywamy pierwotnie dopuszczalną gdy wszystkie wyrazy wolne są $\geq 0$ . Co zapisujemy $b\geq 0$ .

Jak pokazaliśmy poprzednio każdemu wierzchołkowi odpowiada co najmniej jedna tablica sympleks pierwotnie dopuszczalna. Dokładniej tyle tablic ile jest możliwości wyboru zmiennych (nie)bazowych.

Stwierdzenie 5.1

Pierwotnie dopuszczalne tablice sympleks opisują wierzchołki.

Niech $[A|b]$ będzie tablicą sympleks pierwotnie dopuszczalną. W macierzy wybieramy kolumny tworzące macierz jednostkową. Zmienne odpowiadające tym kolumną nazwiemy bazowymi zaś pozostałe niebazowymi. Zmiennym niebazowym przypisujemy wartość 0. Bazowe zmienne wyliczamy z układu równań po opuszczeniu zmiennych niebazowych. Tak więc zmienne bazowe przyjmują wartości wyrazów wolnych w odpowiedniej kolejności. Otrzymany punkt jest wierzchołkiem gdyż spełnia $n$ nierówności jako równania. $t$ z równań $Ax=b$ i $n-t$ z równań $x_{i}=0$ spełnianych przez zmienne niebazowe. Dodatkowo równania te są liniowo niezależne.

∎

Twierdzenie 5.1

Niech $W=\left\{ x\in R^{{n}}\ |\ Ax^{T}=b,\ x\geq 0\right\}$ będzie wielościanem. Dodatkowo zakładamy, że równania opisujące $W$ są liniowo niezależne - czyli $rzA=t=$ liczba równań. Niech $p$ będzie wierzchołkiem $W$ . Wówczas:

a) Liczba niezerowych współrzędnych wierzchołka $p$ jest nie większa niż liczba równań.

b) Istnieje taka odwracalna podmacierz $B\in\mathbb{R}^{t}_{t}$ macierzy $A$ , że $[B^{{-1}}A|B^{{-1}}b]$ jest tablicą sympleks opisującą wierzchołek $p$ .

c) Niech $B\in\mathbb{R}^{t}_{t}$ będzie odwracalną podmacierzą macierzy $A$ . Wówczas $[B^{{-1}}A|B^{{-1}}b]$ jest tablicą sympleks opisującą wierzchołek $p$ wtedy i tylko wtedy gdy macierz $B$ zawiera wszystkie kolumny $A$ , których indeksy są indeksami niezerowych współrzędnych wierzchołka $p$ .

Stwierdzenie 5.2

Jeżeli w wielościanie $W=\left\{ x\in R^{{n}}\ |\ Ax^{T}=b,\ x\geq 0\right\}$ opisanym $t$ równaniami wierzchołek $p$ ma $t$ niezerowych współrzędnych to jest opisany dokładnie jedną tablicą sympleks.

Przykład 5.1

W tablicy sympleks $\left[\begin{array}[]{ccccccc|c}x_{1}&x_{2}&x_{3}&x_{4}&x_{5}&x_{6}&x_{7}&ww\\ \hline 0&1&5&0&-5&3&0&0\\ 1&0&1&1&-2&1&0&1\\ 0&0&-6&0&-4&1&1&3\end{array}\right]$ możemy wybrać kolumny 1, 2 i 7. Niebazowymi zmiennymi są $x_{3},\, x_{4},\, x_{5},\, x_{6}$ i one przyjmują wartość 0. Wykreślamy kolumny zmiennych niebazowych i zmienne bazowe wyliczamy z równania o macierzy $\left[\begin{array}[]{ccc|c}x_{1}&x_{2}&x_{7}&ww\\ \hline 0&1&0&0\\ 1&0&0&1\\ 0&0&1&3\end{array}\right]$ . Więc $x_{1}=1$ , $x_{2}=0$ i $x_{7}=3$ . Wierzchołkiem jest $p_{1}=(1,0,0,0,0,0,3)$ . Wybierzmy teraz kolumny 2, 4 i 7. Otrzymamy wierzchołek $p_{2}=(0,0,0,1,0,0,3)$ .

Algorytm szukania wierzchołków.

Niech $W=\left\{ x\in R^{{n}}\,|\, Ax=b,x\geq 0\right\}$ będzie

wielościanem. Dodatkowo zakładamy, że równania opisujące $W$ są

liniowo niezależne - czyli $rzA=t=$ liczba równań.

Wybieramy maksymalne kwadratowe podmacierze $B$ macierzy $A$ .

Jeżeli $B$ jest macierzą odwracalną to mnożymy równanie $Ax=b$

przez $B^{{-1}}$ z lewej strony i otrzymujemy tablice sympleks.

Jeżeli otrzymana tablica jest pierwotnie dopuszczalna to opisuje

wierzchołek.

Algorytm opisu krawędzi.

Niech $[A|b]$ będzie tablicą sympleks pierwotnie dopuszczalną

opisującą wierzchołek $p$ . Szukamy krawędzi wychodzących z tego

wierzchołka. Zaczynamy od wybrania $n-1$ równań z tych opisujących

wierzchołek. Nie możemy odrzucać równań z układu $Ax=b$ zatem dla

pewnej zmiennej niebazowej zamiast $x_{i}=0$ przyjmujemy $x_{i}\geq 0$ .

Otrzymujemy opis prostej w której zmienna $x_{i}$ jest

parametrem. Dla ustalenia uwagi przyjmijmy

$A=[A|b]=\left[\begin{array}[]{ccc|ccccc|c}x_{1}&...&x_{t}&x_{{t+1}}&...&x_{i}&...&x_{n}&ww\\ \hline 1&\ldots&0&a_{{1,t+1}}&...&a_{{1,i}}&...&a_{{1,n}}&b_{1}\\ \vdots&\ddots&\vdots&\vdots&\ddots&a_{{j,i}}&\ddots&\vdots&\vdots\\ 0&\ldots&1&a_{{t,t+1}}&\ldots&a_{{t,i}}&\ldots&a_{{t,n}}&b_{t}\end{array}\right]$

Teraz wyliczamy zmienne bazowe $x_{j}=b_{j}-a_{{j,i}}x_{i}$ , dla $1\leq j\leq t$ . Punkty otrzymanej prostej mają

postać $(b_{1}-a_{{1,i}}x_{i},\, b_{2}-a_{{2,i}}x_{i},\,...,b_{t}-a_{{t,i}}x_{i},\, 0,0,...,0,x_{i},0,...,0)=(b_{1},b_{2},...,b_{t},0,0,...,0)+x_{i}(a_{{1,i}},a_{{2,i}},...,a_{{t,i}},0,0,...,0,1,0,...,0)$ , gdzie $x_{i}$ stoi na i-tym miejscu.

Jeżeli wszystkie $a_{{j,i}}\leq 0$ to jedynym ograniczeniem jest

$x_{i}\geq 0$ i otrzymujemy krawędź nieskończoną.

W przeciwnym

przypadku największą wartością $x_{i}$ będzie minimum po wszystkich

dodatnich $a_{{j,i}}$ z liczb $\frac{b_{j}}{a_{{j,i}}}$ czyli liczba

$Min\,\{\frac{b_{j}}{a_{{j,i}}}\ |\ 0\leq j\leq t,\, a_{{j,i}}>0\}$ .

Uwaga 5.1

Liczba $d=Min\,\{\frac{b_{j}}{a_{{j,i}}}\ |\ 0\leq j\leq t,\, a_{{j,i}}>0\}$ wyznacza długość krawędzi. Jeżeli startujemy z wierzchołka $p=(b_{1},b_{2},...,b_{t},0,0,...,0)$ i poruszamy się w kierunku $\alpha=(a_{{1,i}},a_{{2,i}},...,a_{{t,i}},0,0,...,0,1,0,...,0)$ to $p+d\alpha$ jest kolejnym wierzchołkiem. Długością krawędzi jest liczba $d\cdot\|\alpha\|$ .

Uwaga 5.2

Jeżeli minimum $d=0$ to krawędź ma długość 0 ( jest punktem ) i nazywamy ją krawędzią zdegenerowaną.

Twierdzenie 5.2

Niech $TS$ będzie pierwotnie dopuszczalną tablicą sympleks, z ustaloną bazą i opisującą wierzchołek $p$ . Wówczas $TS$ opisuje $n-t$ krawędzi wychodzących z wierzchołka $p$ i wektory kierunkowe tych krawędzi są liniowo niezależne. Wliczamy krawędzie zdegenerowane zaś $n$ oznacza liczbę kolumn i $t$ liczbę wierszy.

Ustawmy wektory kierunkowe w macierz a następnie wykreślmy kolumny zmiennych bazowych. Otrzymaliśmy macierz jednostkową $(n-t)\times(n-t)$ . Zatem wektory były liniowo niezależne.

∎

Uwaga 5.3

Aby opisać wszystkie krawędzie wychodzące z wierzchołka $p$ należy użyć wszystkich tablic sympleks opisujących $p$ .

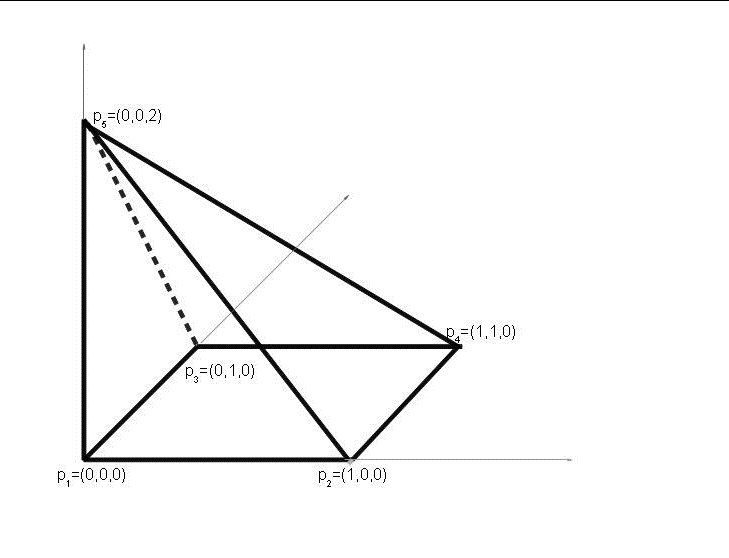
Przykład 5.2

Opiszmy ostrosłup $W\in\mathbf{R^{3}}$ o podstawie kwadratowej z wierzchołkami $p_{1}=(0,0,0),\ p_{2}=(1,0,0),\ p_{3}=(0,1,0),\ p_{4}=(1,1,0)$ i o szczycie w punkcie $p_{5}=(0,0,2)$ .

$\par$

Rys. 5.1. Ostrosłup.

$W$ jest opisane układem nierówności:

$2x_{{1}}+x_{{3}}\leq 2$

$2x_{{2}}+x_{{3}}\leq 2$

$x_{{1}},x_{{2}},x_{{3}}\geq 0$

Przerabiamy nierówności na równania dodając nowe zmienne i otrzymujemy postać kanoniczna:

$2x_{{1}}+x_{{3}}+x_{{4}}=2$

$2x_{{2}}+x_{{3}}+x_{{5}}=2$

$x_{{1}},x_{{2}},x_{{3}},x_{{4}},x_{{5}}\geq 0$

Zapiszmy w postaci tablicy sympleks:

$TS_{1}=\left[\begin{array}[]{ccccc|c}x_{{1}}&x_{{2}}&x_{{3}}&x_{{4}}&x_{{5}}&ww\\ \hline 2&0&1&1&0&2\\ 0&2&1&0&1&2\end{array}\right]$

Zmiennymi bazowymi są $x_{4}$ i $x_{5}$ zaś $TS_{1}$ opisuje wierzchołek:

$\overline{p_{1}}=(0,0,0\,|\, 2,2)$ ,

Poruszamy się w kierunku wierzchołka $\overline{p_{5}}$ krawędzią wyznaczoną przez $x_{3}$ :

$TS_{1}=\left[\begin{array}[]{ccccc|c}&&\downarrow&&&\\ x_{{1}}&x_{{2}}&x_{{3}}&x_{{4}}&x_{{5}}&ww\\ \hline 2&0&1&1&0&2\\ 0&2&(1)&0&1&2\end{array}\right]$ .

Szukamy elementu centralnego.

$Min\left\{\frac{2}{1},\frac{2}{1}\right\}=2$ zatem możemy wybrać dowolny element kolumny 3-ciej.

$TS_{2}=\left[\begin{array}[]{ccccc|c}k_{{1}}&k_{{2}}&&&k_{{3}}&\\ \hline 2&-2&0&1&-1&0\\ 0&2&1&0&1&2\end{array}\right]$ . Zmiennymi bazowymi są teraz $x_{3}$ i $x_{4}$ zaś $TS_{2}$ opisuje wierzchołek $\overline{p_{5}}=(0,0,2\,|\, 0,0)$

Ile krawędzi wychodzi z $W$ ?

Z rysunku widać, że 4, zaś tablica $TS_{2}$ opisuje tylko trzy krawędzie o wektorach kierunkowych
$k_{{1}}\rightarrow(1,0,0,-2,0)$ - krawędź zdegenerowana (długość 0) gdyż $Min\left\{\frac{0}{2},\ast\right\}=0$
$k_{{2}}\rightarrow(0,1,-2,2,0)$ w kierunku wierzchołka $\overline{p_{3}}$
$k_{{3}}\rightarrow(0,0,-1,1,1)$ w kierunku wierzchołka $\overline{p_{1}}$

Wędrując wzdłuż krawędzi zdegenerowanej $k_{1}$ znajdujemy nową TS opisującą $p$ .

Otrzymujemy $\left[\begin{array}[]{ccccc|c}k_{{1}}&&&&&\\ \hline(2)&-2&0&1&-1&0\\ 0&2&1&0&1&2\end{array}\right]\rightarrow\left[\begin{array}[]{ccccc|c}\hline 1&-1&0&\frac{1}{2}&-\frac{1}{2}&0\\ 0&2&1&0&1&2\\ &&B&B&&\end{array}\right]=TS_{3}$

Tablica $TS_{3}$ opisuje dalej wierzchołek $\overline{p_{5}}$ i krawędzie:

$\left[\begin{array}[]{ccccc|c}&k_{{4}}&&k_{{5}}&k_{{6}}&\\ \hline 1&-1&0&\frac{1}{2}&-\frac{1}{2}&0\\ 0&2&1&0&1&2\\ B&&B&&&\end{array}\right]$

$k_{{4}}\rightarrow(1,1,-2,0,0)$ w kierunku wierzchołka $\overline{p_{4}}$

$k_{{5}}\rightarrow(-\frac{1}{2},0,0,1,0)$ - zdegenerowana $k_{{6}}=-\frac{1}{2}k_{{1}}$

$k_{{6}}\rightarrow(\frac{1}{2},0,-1,0,1)$ w kierunku wierzchołka $\overline{p_{2}}$

Definicja 5.2

Tablicą Sympleks opisującą zadanie programowania liniowego

$Max\left\{\; x_{0}=c\bullet x\,+b_{0}\,|\; Ax=b,x\geq 0\right\}$

nazywamy taką macierz, w której pierwszy wiersz reprezentuje równanie $x_{0}-c\bullet x\,=b_{0}$ , pozostałe wiersze równania $[A|b]$ i macierz ta zawiera podmacierz jednostkową. Zwyczajowo pierwszy wiersz - opisujący funkcję celu jest oddzielony linią poziomą. Podobnie znak równości przedstawiamy jako linię pionową.

Tablicę sympleks nazywamy dualnie dopuszczalną gdy w wierszu kosztów zredukowanych (nad kreską ) wszystkie wyrazy są $\geq 0$ , dla zadania typu Max lub są $\leq 0$ , dla zadania typu Min.

Przykład 5.3

Tablicą sympleks dla zadania

Max $x_{0}=2x_{1}+6x_{2}-3x_{3}$ , gdy:

$x_{1}+2x_{2}-3x_{3}+x_{4}=3$

$2x_{1}+3x_{2}-5x_{3}+x_{5}=7$

$2x_{1}-3x_{2}-7x_{3}+x_{6}=8$

$x_{1}\geq 0$ , $x_{2}\geq 0$ , $x_{3}\geq 0$

jest

$\left[\begin{array}[]{ccccccc|c}x_{0}&x_{1}&x_{2}&x_{3}&x_{4}&x_{5}&x_{6}&WW\\ 1&-2&-6&3&0&0&0&0\\ \hline 0&1&2&-3&1&0&0&3\\ 0&2&3&-5&0&1&0&7\\ 0&2&-3&-7&0&0&1&8\end{array}\right]$

Funkcję celu zastąpiliśmy równaniem $x_{0}-2x_{1}-6x_{2}+3x_{3}=0$ zaś podmacierz jednostkowa powstaje z kolumn odpowiadających zmiennym o indeksach 0,4,5 i 6.

Uwaga 5.4

Ponieważ w algorytmie metody sympleks kolumna odpowiadająca zmiennej $x_{0}$ nie zmienia się więc zwykle ją pomijamy.

Zadania

Ćwiczenie 5.1

Poniższe dwie tablice sympleks opisują to samo zadanie PL.

wylicz zmienne od $a$ do $l$ .

1	0	0	2	-3	5
2	1	0	-2	d	e
-3	a	b	c	2	4

oraz

7	g	h	0	-7	-3
-4	1	2	i	5	14
f	0	1	j	k	$l$

Ćwiczenie 5.2

Wiedząc, że poniższe tablice sympleks dotyczą tego samego zadania programowania liniowego wyznacz nieznane współczynniki od $a$ do $k$ .

$\left[\begin{array}[]{ccccc|c}a&b&c&4&-2&-6\\ \hline 3&1&0&d&3&e\\ 7&0&1&1&6&f\end{array}\right]$ oraz $\left[\begin{array}[]{ccccc|c}4&g&0&10&0&-2\\ \hline 1&h&0&3&1&2\\ i&-2&1&j&k&3\end{array}\right]$

Ćwiczenie 5.3

Wiedząc, że punkt $p=(3,0,0,2,0,0,)$ jest wierzchołkiem wielościanu

$W=\{ x\,|\, Ax=b,\: x\geq 0\}$ , gdzie

$A=\left[\begin{array}[]{cccccc}2&3&-2&1&-1&1\\ 2&-1&-5&-3&3&0\\ 1&3&0&2&-2&1\end{array}\right]\: b=\left[\begin{array}[]{c}8\\ 0\\ 7\end{array}\right]$

wypisz wszystkie takie macierze $B$ , zawarte w $A$ , że $[B^{{-1}}A|B^{{-1}}b]$

jest tablicą sympleks opisującą $p$ .

5.2. Metoda sympleks

Wędrowanie między wierzchołkami, eliminacja Gaussa - Jordana.

W zadaniu PL mamy wierzchołek $p$ opisany tablicą sympleks. Dla ustalenia uwagi przyjmijmy $\left[\begin{array}[]{c|ccc|ccccc|c}x_{0}&x_{1}&...&x_{t}&x_{{t+1}}&...&x_{i}&...&x_{n}&ww\\ 1&0&\ldots&0&-c_{{t+1}}&...&-c_{{i}}&...&-c_{{n}}&b_{0}\\ \hline 0&1&\ldots&0&a_{{1,t+1}}&...&a_{{1,i}}&...&a_{{1,n}}&b_{1}\\ \vdots&\vdots&\ddots&\vdots&\vdots&\ddots&a_{{j,i}}&\ddots&\vdots&\vdots\\ 0&0&\ldots&1&a_{{t,t+1}}&\ldots&a_{{t,i}}&\ldots&a_{{t,n}}&b_{t}\end{array}\right]$

Zakładamy, że krawędź odpowiadająca zmiennej $x_{i}$ jest skończona i szukamy tablicy sympleks opisującej drugi koniec tej krawędzi.

Wyliczamy minimum po wszystkich dodatnich $a_{{j,i}}$ z liczb $\frac{b_{j}}{a_{{j,i}}}$ czyli liczbę

$Min_{j}\{\frac{b_{j}}{a_{{j,i}}}\,|\, a_{{j,i}}>0\}$ . Wybieramy dowolny współczynnik $a_{{j,i}}$ , na którym osiągane jest minimum. Nazywamy go elementem centralnym. Na następnej tablicy zaznaczony będzie nawiasem.

$\left[\begin{array}[]{c|ccccc|ccccc|c}x_{0}&x_{1}&\ldots&x_{j}&\ldots&x_{t}&x_{{t+1}}&...&x_{i}&...&x_{n}&ww\\ 1&0&\ldots&0&\ldots&0&-c_{{t+1}}&...&-c_{{i}}&...&-c_{{n}}&b_{0}\\ \hline 0&1&\ldots&0&\ldots&0&a_{{1,t+1}}&...&a_{{1,i}}&...&a_{{1,n}}&b_{1}\\ \vdots&\vdots&\ddots&\vdots&\ddots&\vdots&\vdots&\ddots&\ldots&\ddots&\vdots&\vdots\\ 0&0&\ldots&1&\ldots&0&a_{{j,t+1}}&\ldots&(a_{{j,i}})&\ldots&a_{{j,n}}&b_{j}\\ \vdots&\vdots&\ddots&\vdots&\ddots&\vdots&\vdots&\ddots&\ldots&\ddots&\vdots&\vdots\\ 0&0&\ldots&0&\ldots&1&a_{{t,t+1}}&\ldots&a_{{t,i}}&\ldots&a_{{t,n}}&b_{t}\end{array}\right]$

Teraz j - ty wiersz dzielimy przez $a_{{j,i}}$ zaś od każdego innego wiersza $k$ odejmujemy poprawiony j-ty wiersz pomnożony przez $a_{{k,i}}$ - czyli zerujemy pozostałe miejsca k-tej kolumny. Otrzymujemy macierz:

$\left[\begin{array}[]{c|ccccc|ccccc|c}x_{0}&x_{1}&\ldots&x_{j}&\ldots&x_{t}&x_{{t+1}}&...&x_{i}&...&x_{n}&ww\\ 1&0&\ldots&d_{0}&\ldots&0&-c_{{t+1}}^{*}&...&0&...&-c_{{n}}^{*}&b_{0}^{*}\\ \hline 0&1&\ldots&d_{1}&\ldots&0&a_{{1,t+1}}*&...&0&...&a_{{1,n}}^{*}&b_{1}*\\ \vdots&\vdots&\ddots&\vdots&\ddots&\vdots&\vdots&\ddots&\ldots&\ddots&\vdots&\vdots\\ 0&0&\ldots&d_{j}&\ldots&0&a_{{j,t+1}}^{*}&\ldots&1&\ldots&a_{{j,n}}^{*}&b_{j}^{*}\\ \vdots&\vdots&\ddots&\vdots&\ddots&\vdots&\vdots&\ddots&\ldots&\ddots&\vdots&\vdots\\ 0&0&\ldots&d_{t}&\ldots&1&a_{{t,t+1}}^{*}&\ldots&0&\ldots&a_{{t,n}}^{*}&b_{t}^{*}\end{array}\right]$ ,

gdzie $d_{0}=\frac{c_{i}}{a_{{j,i}}},d_{1}=-\frac{a_{{1,i}}}{a_{{j,i}}},...,\\ d_{{j-1}}=-\frac{a_{{j-1,i}}}{a_{{j,i}}},d_{j}=\frac{1}{a_{{j,i}}},d_{{j+1}}=-\frac{a_{{j+1,i}}}{a_{{j,i}}},...,d_{t}=-\frac{a_{{t,i}}}{a_{{j,i}}}$

Otrzymaliśmy tablicę sympleks. Z bazy wypadła zmienna $x_{j}$ a doszła zmienna $x_{i}$ .

Test optymalności i koszty zredukowane. Rozważamy zadanie typu

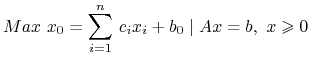$Max\ x_{0}=\sum _{{i=1}}^{n}\, c_{i}x_{i}+b_{0}\;|\; Ax=b,\ x\geq 0$

opisane tablicą sympleks TS. Oznacza to, że w górnym wierszu TS mamy kolejno liczby

$1,-c_{1},-c_{2},...,-c_{n}\,|\, b_{0}$

. Ponieważ jest to tablica sympleks wszystkie współczynniki $c_{i}$ odpowiadające zmiennym bazowym są równe 0.

Jeżeli koszt zredukowany $-c_{j}$ odpowiadający zmiennej niebazowej $x_{j}$ jest $<0$ ( $c_{j}>0$ ) to krawędź wyznaczona przez zmienną $x_{j}$ jest poprawiająca. Ponieważ wędrując tą krawędzią zmieniamy tylko zmienne bazowe nie mające wpływu na funkcję celu i zwiększamy liczbę $x_{0}=c_{j}x_{j}+b_{0}$ .

Jeżeli koszt zredukowany $-c_{j}$ odpowiadający zmiennej niebazowej $x_{j}$ jest = 0 ( $c_{j}=0$ ) to krawędź wyznaczona przez zmienną $x_{j}$ jest neutralna.

Jeżeli koszt zredukowany $-c_{j}$ odpowiadający zmiennej niebazowej $x_{j}$ jest $>0$ ( $c_{j}<0$ ) to krawędź wyznaczona przez zmienną $x_{j}$ jest pogarszająca. Ponieważ wędrując tą krawędzią zmieniamy tylko zmienne bazowe nie mające wpływu na funkcję celu i zmniejszamy liczbę

$x_{0}=c_{j}x_{j}+b_{0}$

Twierdzenie 5.3

Jeżeli w tablicy sympleks opisującej zadanie $Max\ x_{0}=\sum _{{i=1}}^{n}\, c_{i}x_{i}+b_{0}\;|\; Ax=b,\ x\geq 0$ wszystkie koszty zredukowane są $\geq 0$ to tablica ta opisuje wierzchołek optymalny zadania zaś w prawym górnym rogu tablicy otrzymujemy optymalną wartość funkcji celu.

Jeżeli w tablicy sympleks wszystkie koszty zredukowane są $\geq 0$ to funkcja celu $x_{0}=\sum _{{i=1}}^{n}\, c_{i}x_{i}+b_{0}$ może być zapisana tylko przy pomocy zmiennych niebazowych $x_{0}=\sum _{{x_{i}\ niebazowe}}\, c_{i}x_{i}+b_{0}$ gdyż dla zmiennych bazowych $c_{i}=0$ . Funkcja celu $x_{0}$ przyjmuje w wierzchołku opisanym tablicą sympleks wartość $b_{0}$ a dla pozostałych punktów wielościanu $x_{0}\leq b_{0}$ .

∎

Algorytm prosty metody sympleks.

Rozważamy zadanie typu $Max\, x_{0}=\sum _{{i=1}}^{n}\, c_{i}x_{i}+b_{0}\;|\; Ax=b$

0) Start: Dana tablica sympleks pierwotnie dopuszczalna.

1) Test optymalności i wybór kolumny głównej.

1a) Jeżeli wszystkie koszty zredukowane są nieujemne

to STOP. Tablica opisuje wierzchołek optymalny.

1b) Jeżeli nie to wybieramy kolumnę $i$ , w której koszt

zredukowany jest ujemny.

2) Test nieograniczoności i wybór elementu centralnego.

2a) Jeżeli wszystkie elementy kolumny $i$ są

niedodatnie to STOP. Funkcja celu jest nieograniczona.

2b) Jeżeli istnieją $a_{{k,i}}>0$ to jako element centralny wybieramy taki $a_{{j,i}}$ ,

że $\frac{b_{j}}{a_{{j,i}}}=Min_{k}\{\frac{b_{k}}{a_{{k,i}}}\ ;\, a_{{k,i}}\geq 0\}$ .

3) Znajdujemy tablicę sympleks opisującą drugi koniec krawędzi

metodą Gaussa - Jordana, GOTO 1).

Przykład 5.4

Rozwiązujemy zadanie: Max $x_{0}=2x_{1}+6x_{2}-3x_{3}$ , gdy:

$x_{1}+2x_{2}-3x_{3}\leq 3$

$2x_{1}+5x_{2}-5x_{3}\leq 7$

$2x_{1}-3x_{2}-7x_{3}\leq 8$

$x_{1}\geq 0$ , $x_{2}\geq 0$ , $x_{3}\geq 0$

Postacią kanoniczną jest:

Max $x_{0}=2x_{1}+6x_{2}-3x_{3}$ , gdy:

$x_{1}+2x_{2}-3x_{3}+x_{4}=3$

$2x_{1}+5x_{2}-5x_{3}+x_{5}=7$

$2x_{1}-3x_{2}-7x_{3}+x_{6}=8$

$x_{1}\geq 0$ , $x_{2}\geq 0$ , $x_{3}\geq 0$

Wierzchołkowi $p_{1}=(0,0,0,3,7,8)$ odpowiada TS

$\left[\begin{array}[]{c|cccccc|c}1&-2&-6&3&0&0&0&0\\ \hline 0&(1)&2&-3&1&0&0&3\\ 0&2&5&-5&0&1&0&7\\ 0&2&-3&-7&0&0&1&8\end{array}\right]$

Idziemy krawędzią poprawiająca wyznaczoną przez $x_{1}$

Liczymy $Min\,\{\frac{3}{1},\,\frac{7}{2},\,\frac{8}{2}\}=3$ więc jako element centralny wybieramy $a_{{1,1}}=1$ .

Po przekształceniach Gaussa - Jordana Otrzymujemy

$\left[\begin{array}[]{c|cccccc|c}1&0&-2&-3&2&0&0&6\\ \hline 0&1&2&-3&1&0&0&3\\ 0&0&1&(1)&-2&1&0&1\\ 0&0&-7&-1&-2&0&1&2\end{array}\right]$

Tablica ta opisuje wierzchołek $p_{2}=(3,0,0,0,1,2,)$

Idziemy krawędzią poprawiająca wyznaczoną przez $x_{2}$

Liczymy $Min\,\{\frac{3}{2},\,\frac{1}{1},\,*\}=1$ więc jako element centralny wybieramy $a_{{2,3}}=1$ .

Po przekształceniach Gaussa - Jordana Otrzymujemy

$\left[\begin{array}[]{c|cccccc|c}1&0&1&0&-4&3&0&9\\ \hline 0&1&5&0&-5&3&0&6\\ 0&0&1&1&-2&1&0&1\\ 0&0&-6&0&-4&1&1&3\end{array}\right]$

Kolumna odpowiadająca zmiennej $x_{4}$ ma ujemny koszt zredukowany więc na krawędzi przez nią wyznaczonej

$k=\{(6+5x_{4},0,1+2x_{4},x_{4},0,3+4x_{4})\;|\; x_{4}\geq 0\}$ funkcja celu $x_{0}=9-x_{2}+4x_{4}-3x_{5}=9+4x_{4}$ rośnie w nieskończoność.

5.3. Wymiar zbioru punktów optymalnych.

Twierdzenie 5.4

Niech zadanie $Max\ x_{0}=\sum _{{i=1}}^{n}\, c_{i}x_{i}+b_{0}\;|\; Ax=b,\ x\geq 0$ będzie opisane tablicą sympleks pierwotnie i dualnie dopuszczalną. Wówczas zbiór punktów dopuszczalnych zadania ma wymiar nie większy niż liczba zer niebazowych.

Przyjmijmy, że tablica sympleks ma $t$ wierszy i $n$ kolumn. Zbiór punktów optymalnych $P$ jest wielościanem w przestrzeni $\mathbb{R}^{n}$ opisanym równaniami z tablicy, nierównościami $x_{i}\geq 0$ i funkcją celu. Ale jeżeli punkt $q$ jest optymalny to jego współrzędne odpowiadające kolumnom poprawiającym muszą być równe zero. Tak więc zbiór punktów optymalnych jest przecięciem stożka opisanego nierównościami $x_{i}\geq 0$ i podprzestrzeni $V$ opisanej równaniami z tablicy i równaniami $x_{i}=0$ dla $i$ odpowiadających kolumnom poprawiającym. Równania te są liniowo niezależne więc $dim\, V=n-(t+n-t-k)=k$ . Zatem $dim\, P\leq dim\, V=k$ .

∎

Z twierdzenia 5.4 otrzymujemy bezpośrednio:

Wniosek 5.1

Jeżeli w tablicy sympleks pierwotnie dopuszczalnej wszystkie koszty zredukowane odpowiadające zmiennym niebazowym są $>0$ to tablica ta opisuje jedyny wierzchołek optymalny zadania.

Wniosek 5.2

Jeżeli w tablicy sympleks pierwotnie i dualnie dopuszczalnej każda krawędź neutralna opisywana przez tą tablicę jest niezdegenerowana to wymiar zbioru punktów optymalnych jest równy liczbie tych krawędzi. ( Liczbie zer niebazowych w tablicy sympleks.)

Przyjmijmy, że tablica sympleks opisuje wierzchołek $p$ i wychodzące z niego krawędzie neutralne $k_{1},k_{2},...,k_{s}$ . Wtedy wymiar zbioru punktów optymalnych $d$ spełnia warunki: $d\leq dim\, af(p+lin\{ k_{1},k_{2},...,k_{s}\})=s$ , gdyż na mocy twierdzenia 5.2 wektory krawędzi są liniowo niezależne. Z drugiej strony $d\geq s$ na mocy twierdzenia 5.4.

∎

Wniosek 5.3

Jeżeli tablica sympleks pierwotnie i dualnie dopuszczalna o $t$ wierszach pod kreską ma nad kreską dokładnie $t+1$ zer, to:

a) jeżeli krawędź neutralna jest niezdegenerowana to zbiorem punktów optymalnych zadania jest ta krawędź,

b) jeżeli krawędź neutralna jest zdegenerowana to tablica ta opisuje jedyny wierzchołek optymalny zadania.

Ad a) Zbiór punktów optymalnych jest ścianą wielościanu - obszaru dopuszczalnego, zawiera krawędź neutralną opisaną tablicą sympleks i na mocy twierdzenia 5.3 ma wymiar $\leq 1$ więc jest tą krawędzią.

Ad b) Przenumerujmy kolumny tak by tablica sympleks miała postać

$[A|b]=\left[\begin{array}[]{ccc|cccccc|c}0&...&0&0&d_{{t+2}}&...&d_{i}&...&d_{n}&b_{0}\\ \hline 1&\ldots&0&a_{{1,t+1}}&a_{{1,t+2}}&...&a_{{1,i}}&...&a_{{1,n}}&b_{1}\\ \vdots&\ddots&\vdots&\vdots&\vdots&\ddots&a_{{j,i}}&\ddots&\vdots&\vdots\\ 0&\ldots&1&a_{{t,t+1}}&a_{{t,t+2}}&\ldots&a_{{t,i}}&\ldots&a_{{t,n}}&b_{t}\end{array}\right]$ ,

gdzie pierwszych $t$ zmiennych jest bazowych zaś $d_{i}>0$ dla $i>t+1$ .

Niech $q=(q_{1},q_{2},...,q_{n})$ będzie punktem optymalnym. Porównując wartości funkcji celu w punkcie $p$ opisanym tablicą i w punkcie $q$ otrzymujemy $b_{0}=x_{0}(p)=x_{0}(q)=-\sum _{{i=t+2}}^{n}d_{i}q_{i}$ . Więc $i>t+1\Rightarrow q_{i}=0$ .

Krawędź opisana $t+1$ -szą kolumną jest zdegenerowana więc istnieje wiersz $j$ taki, że $a_{{j,t+1}}>0$ i $b_{j}=0$ . Po wstawieniu do $j$ -tego równania $q$ otrzymujemy $q_{j}+a_{{j,t+1}}q_{{j,t+1}}=b_{j}=0$ i stąd $q_{{j,t+1}}=0$ . W rezultacie punkt $q$ spełnia ten sam układ równań co punkt $p$ więc $q=p$ .

∎

Przykład 5.5

Jeżeli w tablica sympleks pierwotnie i dualnie dopuszczalna o $t$ wierszach pod kreską ma nad kreską więcej niż $t+1$ zer, to wymiar zbioru punktów optymalnych może być każdą liczbą między 0 a liczbą zer niebazowych. Zobaczmy to na przykładzie zadania opisanego tablicą:

$\left[\begin{array}[]{ccccccc|c}0&0&0&0&0&0&3&0\\ \hline 1&0&0&0&0&1&1&1\\ 0&1&0&0&0&0&1&2\\ 0&0&1&0&\left(1\right)&-2&1&0\\ 0&0&0&1&-1&1&1&0\end{array}\right]$

Wierzchołek optymalny ma współrzędne $p_{1}=(1,2,0,0,0,0,0)$ . Mamy dodatkowo dwie kolumny opisujące zdegenerowane krawędzie neutralne 5-tą i 6-tą. Pokażemy, że zbiór punktów optymalnych jest trójkątem. Po eliminacji Gaussa - Jordana otrzymujemy inną tablicę opisującą ten sam wierzchołek.

$\left[\begin{array}[]{ccccccc|c}0&0&0&0&0&0&3&0\\ \hline 1&0&0&0&0&\left(1\right)&1&1\\ 0&1&0&0&0&0&1&2\\ 0&0&1&0&1&-2&1&0\\ 0&0&1&1&0&-1&2&0\end{array}\right]$

Teraz 6-ta kolumna opisuje krawędź niezdegenerowaną. Dochodzimy nią do wierzchołka $p_{2}=(0,2,0,1,2,1,0)$ opisanego tablicą:

$\left[\begin{array}[]{ccccccc|c}0&0&0&0&0&0&3&0\\ \hline 1&0&0&0&0&1&1&1\\ 0&1&0&0&0&0&1&2\\ 2&0&1&0&1&0&3&2\\ 1&0&\left(1\right)&1&0&0&3&1\end{array}\right]$

Teraz 3-ta kolumna opisuje kolejną krawędź niezdegenerowaną. Dochodzimy nią do wierzchołka $p_{3}=(0,2,1,0,1,1,0)$ opisanego tablicą:

$\left[\begin{array}[]{ccccccc|c}0&0&0&0&0&0&3&0\\ \hline(1)&0&0&0&0&1&1&1\\ 0&1&0&0&0&0&1&2\\ 1&0&0&-1&1&0&0&1\\ 1&0&1&1&0&0&3&1\end{array}\right]$

Z tej tablicy możemy dojść do tablicy opisującej wierzchołek $p_{1}$ wybierając element centralny w wyznaczonym miejscu.

Zadania

Ćwiczenie 5.4

Opisz prosty algorytm metody sympleks na przykładzie zadania:

Max $x_{0}=2x_{1}+5x_{2}-3x_{3}$ , gdy:

$x_{1}+2x_{2}+3x_{3}\leq 4$

$x_{1}+3x_{2}+x_{3}\leq 5$

$2x_{1}-3x_{2}+7x_{3}\leq 9$

$x_{1}\geq 0$ , $x_{2}\geq 0$ , $x_{3}\geq 0$

Ćwiczenie 5.5

Opisz wszystkie punkty optymalne zadania:

$Max\ x_{0}=-4x_{1}+2x_{2}+3x_{3}\\ \begin{array}[]{rl}2x_{1}-x_{2}+x_{3}&\leq 2\\ -6x_{1}+3x_{2}-2x_{3}&\leq 2\\ -7x_{1}+4x_{2}-3x_{3}&\leq 2\end{array}$

$x_{1}\geq 0$ , $x_{2}\geq 0$ , $x_{3}\geq 0$

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Optymalizacja I

Zagadnienia

5. Tablice sympleks

5.1. Tablice sympleks

Definicja 5.1

Stwierdzenie 5.1

Twierdzenie 5.1

Stwierdzenie 5.2

Przykład 5.1

Algorytm szukania wierzchołków.

Algorytm opisu krawędzi.

Uwaga 5.1

Uwaga 5.2

Twierdzenie 5.2

Uwaga 5.3

Przykład 5.2

Definicja 5.2

Przykład 5.3

Uwaga 5.4

Zadania

Ćwiczenie 5.1

Ćwiczenie 5.2

Ćwiczenie 5.3

5.2. Metoda sympleks

Twierdzenie 5.3

Algorytm prosty metody sympleks.

Przykład 5.4

5.3. Wymiar zbioru punktów optymalnych.

Twierdzenie 5.4

Wniosek 5.1

Wniosek 5.2

Wniosek 5.3

Przykład 5.5

Zadania

Ćwiczenie 5.4

Ćwiczenie 5.5