« 9. Warunki drugiego rzędu  Spis treści  11. Teoria wrażliwości »  

Zagadnienia

10. Teoria dualności

W tym rozdziale omówimy elementy teorii dualności, tzn. innej charakteryzacji optymalności rozwiązania zadania optymalizacyjnego z ograniczeniami nierównościowymi. Teoria ta odróżnia się od poprzednio opisywanego podejścia Kuhna-Tucker'a tym, że nie wymagamy różniczkowalności funkcji celu f i funkcji ograniczeń g_{i}. Ponadto, przy odpowiednich założeniach, rozwiązanie pierwotnego zadania optymalizacyjnego możemy łatwo uzyskać z rozwiązania tzw. zadania do niego dualnego. Niezależnie od zadania pierwotnego, zadanie dualne polega na maksymalizacji wklęsłej funkcji celu po nieujemnym oktancie. Jak zobaczymy w następnych rozdziałach, wklęsłość jest cechą gwarantującą dobrą zbieżność metod numerycznych. Prosty zbiór punktów dopuszczalnych dodatkowo przyspiesza działanie i ułatwia implementację algorytmów numerycznych. Nie należy zapominać także o tym, że zadanie dualne jest czasami łatwiejsze do rozwiązania metodami analitycznymi, czego przykłady zobaczymy w zadaniach na końcu niniejszego rozdziału.

10.1. Warunek dostateczny

Definicja 10.1

Niech A,B będą dowolnymi zbiorami, zaś h:A\times B\to\mathbb{R} funkcją. Punkt ({\bar{\mathbf{x}}},\bar{\mu})\in A\times B nazywamy punktem siodłowym funkcji h, jeśli

h({\bar{\mathbf{x}}},\mu)\le h({\bar{\mathbf{x}}},\bar{\mu})\le h(\mathbf{x},\bar{\mu}),\qquad\forall\ \mathbf{x}\in A,\ \mu\in B.
Przykład 10.1
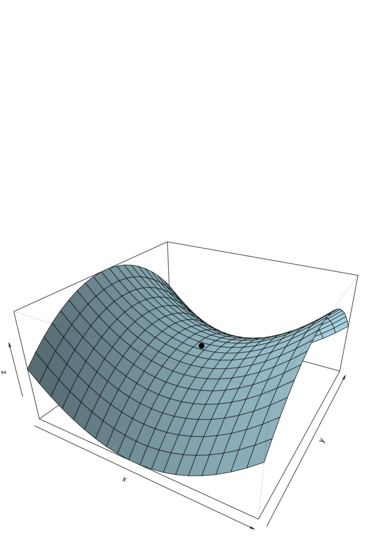
Wykres funkcji $(x,y)\mapsto x^{2}-y^{2}$
Rys. 10.1. Wykres funkcji (x,y)\mapsto x^{2}-y^{2}.

Najprostszym przykładem punktu siodłowego jest ”środek siodła” (patrz rys. 10.1): A,B=\mathbb{R}, h(x,\mu)=x^{2}-\mu^{2} ma punkt siodłowy w (0,0). Funkcja h ma minimum w (0,0) ze względu na zmienną x i maksimum ze względu na \mu.

Okazuje się, że punkt siodłowy funkcji Lagrange'a jest związany z rozwiązaniem globalnym problemu optymalizacji z ograniczeniami nierównościowymi:

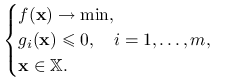\begin{cases}f(\mathbf{x})\to\min,&\\ g_{i}(\mathbf{x})\le 0,\quad i=1,\ldots,m,&\\ \mathbf{x}\in\mathbb{X}.\end{cases} (10.1)

Przypomnijmy, że przez W oznaczamy zbiór punktów dopuszczalnych, tj.

W=\big\{\mathbf{x}\in\mathbb{X}:\quad g_{1}(\mathbf{x})\le 0,\ldots,g_{m}(\mathbf{x})\le 0\big\}.
Twierdzenie 10.1

Jeśli ({\bar{\mathbf{x}}},\bar{\mu})\in W\times[0,\infty)^{m} jest punktem siodłowym funkcji Lagrange'a na W\times[0,\infty)^{m}

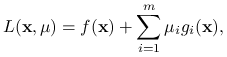L(\mathbf{x},\mu)=f(\mathbf{x})+\sum _{{i=1}}^{m}\mu _{i}g_{i}(\mathbf{x}),

tzn.

L({\bar{\mathbf{x}}},\mu)\le L({\bar{\mathbf{x}}},\bar{\mu})\le L(\mathbf{x},{\bar{\mu}}),\qquad\forall\ \mathbf{x}\in W,\ \mu\in[0,\infty)^{m},

to {\bar{\mathbf{x}}} jest rozwiązaniem globalnym problemu (10.1) oraz {\bar{\mu}}_{i}g_{i}({\bar{\mathbf{x}}})=0 dla i=1,\ldots,m.

Dowód

Udowodnimy najpierw, że {\bar{\mu}}_{i}g_{i}({\bar{\mathbf{x}}})=0 dla i=1,\ldots,m. Nierówność L({\bar{\mathbf{x}}},\mu)\le L({\bar{\mathbf{x}}},{\bar{\mu}}) możemy rozwinąć następująco:

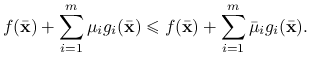f({\bar{\mathbf{x}}})+\sum _{{i=1}}^{m}\mu _{i}g_{i}({\bar{\mathbf{x}}})\le f({\bar{\mathbf{x}}})+\sum _{{i=1}}^{m}{\bar{\mu}}_{i}g_{i}({\bar{\mathbf{x}}}).

Zatem dla każdego \mu\in[0,\infty)^{m} mamy

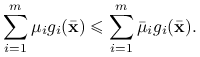\sum _{{i=1}}^{m}\mu _{i}g_{i}({\bar{\mathbf{x}}})\le\sum _{{i=1}}^{m}{\bar{\mu}}_{i}g_{i}({\bar{\mathbf{x}}}).

W szczególności, dla \mu={\bar{\mu}}/2 dostajemy

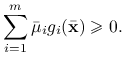\sum _{{i=1}}^{m}{\bar{\mu}}_{i}g_{i}({\bar{\mathbf{x}}})\ge 0.

Wiemy, że {\bar{\mathbf{x}}} jest punktem dopuszczalnym ({\bar{\mathbf{x}}}\in W), czyli g_{i}({\bar{\mathbf{x}}})\le 0 dla i=1,\ldots,m. Pamiętając, że {\bar{\mu}} ma wszystkie współrzędne nieujemne wnioskujemy, iż \sum _{{i=1}}^{m}{\bar{\mu}}_{i}g_{i}({\bar{\mathbf{x}}})=0 oraz każdy wyraz jest niedodatni. Stąd już wynika, że {\bar{\mu}}_{i}g_{i}({\bar{\mathbf{x}}})=0 dla i=1,\ldots,m.

Skorzystamy teraz z drugiej nierówności L({\bar{\mathbf{x}}},{\bar{\mu}})\le L(\mathbf{x},{\bar{\mu}}) dla \mathbf{x}\in W, aby wykazać globalną optymalność {\bar{\mathbf{x}}}. Nierówność tą rozpisujemy następująco:

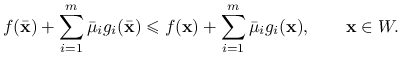f({\bar{\mathbf{x}}})+\sum _{{i=1}}^{m}{\bar{\mu}}_{i}g_{i}({\bar{\mathbf{x}}})\le f(\mathbf{x})+\sum _{{i=1}}^{m}{\bar{\mu}}_{i}g_{i}(\mathbf{x}),\qquad\mathbf{x}\in W.

Z pierwszej części dowodu mamy \sum _{{i=1}}^{m}{\bar{\mu}}_{i}g_{i}({\bar{\mathbf{x}}})=0. Z faktu, że \mathbf{x}\in W dostajemy \sum _{{i=1}}^{m}{\bar{\mu}}_{i}g_{i}(\mathbf{x})\le 0. Czyli

f({\bar{\mathbf{x}}})\le f(\mathbf{x}),\qquad\mathbf{x}\in W.
∎
Uwaga 10.1

\

  1. W powyższym twierdzeniu nie zakładamy otwartości 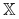\mathbb{X} ani ciągłości funkcji f i g_{i}.

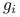  2. Zbiór punktów dopuszczalnych 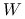W nie musi być wypukły.

  3. Nie ma żadnych warunków regularności.

  4. Tw. 10.1 nie podaje sposobu szukania punktu siodłowego. Można go znaleźć np. przy pomocy warunków koniecznych pierwszego rzędu, a twierdzenie 10.1 używać jako warunek dostateczny.

  5. Tw. 10.1 pełni ważną rolę teoretyczną (podejście dualne) i służy do budowy algorytmów numerycznych rozwiązujących zadanie (10.1).

10.2. Warunek konieczny dla programowania wypukłego

W tym podrozdziale zakładamy, że w problemie (10.1) zbiór \mathbb{X}\subset\mathbb{R}^{n} jest wypukły oraz funkcje f,g_{i}:\mathbb{X}\to\mathbb{R}, i=1,\ldots,m, są wypukłe. Dla takiego zadania optymalizacyjnego warunek punktu siodłowego funkcji Lagrange'a jest warunkiem koniecznym dla rozwiązania globalnego. Zaczniemy od prostszego przypadku, gdy wszystkie funkcje są różniczkowalne, by przejść później do twierdzenia nie wymagającego różniczkowalności. Jak wspomnieliśmy wcześniej, brak wymagania różniczkowalności odróżnia metodę punktu siodłowego od opisanej wcześniej metody Kuhn'a-Tucker'a.

Lemat 10.1

Załóżmy, że zbiór \mathbb{X} w problemie programowania wypukłego jest otwarty oraz funkcje f i g_{i}, i=1,\ldots,m, są różniczkowalne w punkcie {\bar{\mathbf{x}}}. Jeśli {\bar{\mathbf{x}}} jest rozwiązaniem lokalnym (10.1) i spełniony jest jeden z warunków regularności: liniowej niezależności, afiniczności lub Slatera, to istnieje {\bar{\mu}}\in[0,\infty)^{m}, taki że ({\bar{\mathbf{x}}},{\bar{\mu}}) jest punktem siodłowym funkcji Lagrange'a na przestrzeni \mathbb{X}\times[0,\infty)^{m}.

Dowód

Na mocy twierdzenia 5.2 istnieje wektor mnożników Langrange'a {\bar{\mu}}\in[0,\infty)^{m}, dla których spełniony jest warunek optymalności pierwszego rzędu (spełnienie założeń tego twierdzenia wynika z regularności punktu {\bar{\mathbf{x}}} oraz rozważań rozdziału 6). Teza wynika teraz z ćwiczenia 10.1.

∎
Uwaga 10.2

Na mocy twierdzenia 7.6 każdy punkt spełniający warunki pierwszego rzędu jest rozwiązaniem globalnym zadania programowania wypukłego. Nie jest zatem ważne, czy wymagać będziemy w powyższym lemacie, aby {\bar{\mathbf{x}}} był rozwiązaniem lokalnym czy globalnym.

Przechodzimy teraz do głównego twierdzenia.

Twierdzenie 10.2

Niech {\bar{\mathbf{x}}}\in\mathbb{X} będzie rozwiązaniem globalnym problemu programowania wypukłego (10.1) oraz istnieje \mathbf{x}^{*}\in\mathbb{X}, taki że g_{i}(\mathbf{x}^{*})<0 dla i=1,\ldots,m. Wówczas istnieje {\bar{\mu}}\in[0,\infty)^{m} o tej własności, że ({\bar{\mathbf{x}}},{\bar{\mu}}) jest punktem siodłowym funkcji Lagrange'a na przestrzeni \mathbb{X}\times[0,\infty)^{m}, tzn.

L({\bar{\mathbf{x}}},\mu)\le L({\bar{\mathbf{x}}},\bar{\mu})\le L(\mathbf{x},{\bar{\mu}}),\qquad\forall\ \mathbf{x}\in\mathbb{X},\ \mu\in[0,\infty)^{m}.

Ponadto, {\bar{\mu}}_{i}g_{i}({\bar{\mathbf{x}}})=0 dla i=1,\ldots,m.

Uwaga 10.3

Punkt siodłowy funkcji Langrange'a jest rozpatrywany na różnych przestrzeniach w tw. 10.1 i 10.2. W drugim ze wspomnianych twierdzeń przestrzeń jest większa, gdyż pierwsza zmienna przebiega cały zbiór \mathbb{X}, a nie tylko zbiór punktów dopuszczalnych W. W sumie, dostajemy równoważność istnienia punktu siodłowego funkcji Lagrange'a i rozwiązania globalnego zadania optymalizacji wypukłej.

Dowód tw. 10.2

Podobnie jak w dowodzie warunku koniecznego pierwszego rzędu, tw. 5.2, główną rolę będzie tutaj odgrywać twierdzenie o oddzielaniu zbiorów wypukłych. Wskaże nam ono wektor mnożników Lagrange'a {\bar{\mu}}.

Oznaczmy g(\mathbf{x})=\big(g_{1}(x),\ldots,g_{m}(\mathbf{x})\big). Zdefiniujmy następujące podzbiory \mathbb{R}^{{m+1}}:

\displaystyle A \displaystyle=\big\{{\bar{\mathbf{y}}}=(y_{0},\mathbf{y})\in\mathbb{R}\times\mathbb{R}^{m}:\quad y_{0}\ge f(\mathbf{x}),\ \mathbf{y}\ge g(\mathbf{x})\text{ dla pewnego $\mathbf{x}\in\mathbb{X}$}\big\},
\displaystyle B \displaystyle=\big\{{\bar{\mathbf{y}}}=(y_{0},\mathbf{y})\in\mathbb{R}\times\mathbb{R}^{m}:\quad y_{0}=f(\mathbf{x}),\ \mathbf{y}=g(\mathbf{x})\text{ dla pewnego $\mathbf{x}\in\mathbb{X}$}\big\},
\displaystyle C \displaystyle=\big\{{\bar{\mathbf{y}}}=(y_{0},\mathbf{y})\in\mathbb{R}\times\mathbb{R}^{m}:\quad y_{0}<f({\bar{\mathbf{x}}}),\ \mathbf{y}<\mathbf{0}\big\}.

Zauważmy, że ostatni ze zbiorów jest ”oszukany”: jest on produktem półprostej kończącej się w minimum f({\bar{\mathbf{x}}}) i ujemnego oktantu. Łatwo widzimy, że jest on wypukły. Z optymalności {\bar{\mathbf{x}}} dostajemy, że B\cap C=\emptyset. Zbiór B nie jest jednak wypukły, więc nie możemy stosować twierdzeń o oddzielaniu. Radą na to jest spostrzeżenie, że zamiast B można brać zbiór wypukły A, który ma również puste przecięcie z C. Przypuśćmy przeciwnie: niech {\bar{\mathbf{y}}}=(y_{0},\mathbf{y})\in A\cap C. Mamy zatem dla pewnego \mathbf{x}^{{\prime}}\in\mathbb{X} następujące nierówności:

y_{0}\ge f(\mathbf{x}^{{\prime}}),\quad\mathbf{y}\ge g(\mathbf{x}^{{\prime}}),\quad y_{0}<f({\bar{\mathbf{x}}}),\quad\mathbf{y}<0.

Wnioskujemy z nich, że f(\mathbf{x}^{{\prime}})<f({\bar{\mathbf{x}}}) oraz g(\mathbf{x}^{{\prime}})<0. A zatem punkt \mathbf{x}^{{\prime}} jest dopuszczalny, zaś funkcja f przyjmuje w nim wartość mniejszą od f({\bar{\mathbf{x}}}). Przeczy to optymalności {\bar{\mathbf{x}}}.

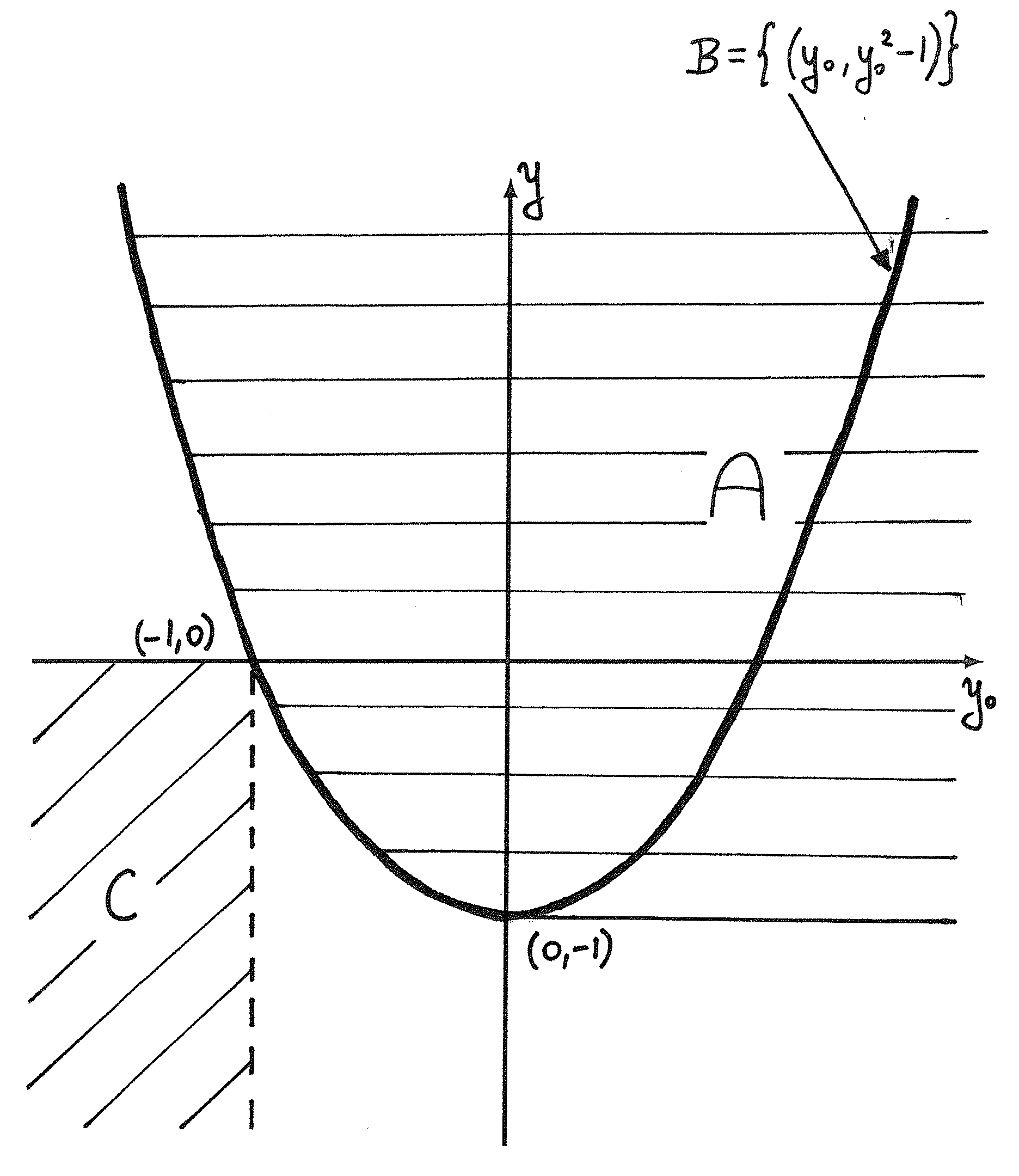
Przykład 10.2

Przed przystąpieniem do dalszej części dowodu popatrzmy na zbiory A,B,C dla następującego problemu optymalizacyjnego:

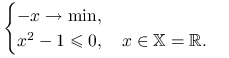\begin{cases}-x\to\min,&\\ x^{2}-1\le 0,\quad x\in\mathbb{X}=\mathbb{R}.&\end{cases}

Rozwiązaniem tego zagadnienia jest \bar{x}=1. Mamy jedno ograniczenie, więc szukane zbiory leżą w przestrzeni \mathbb{R}^{2}. Na rysunku 10.2 znajduje się ich szkic. Zwróćmy uwagę na zależność między zbiorami A i B. Zbiór B jest brzegiem A dla y_{0}\le 0, lecz znajduje się w jego wnętrzu dla y_{0}>0.

Rys. 10.2. Szkic zbiorów A,B,C zdefiniowanych w dowodzie twierdzenia 10.2.

Powróćmy do dowodu. Wypukłość zbioru C już została uzasadniona. Wypukłość A dowodzimy bezpośrednio. Weźmy dwa punkty {\bar{\mathbf{y}}}^{{\prime}},{\bar{\mathbf{y}}}^{{\prime\prime}}\in A oraz \lambda\in(0,1). Istnieją wówczas punkty \mathbf{x}^{{\prime}},\mathbf{x}^{{\prime\prime}}\in\mathbb{X} o następującej własności:

\displaystyle y_{0}^{{\prime}}\ge f(\mathbf{x}^{{\prime}}),\quad\mathbf{y}^{{\prime}}\ge g(\mathbf{x}^{{\prime}}),
\displaystyle y_{0}^{{\prime\prime}}\ge f(\mathbf{x}^{{\prime\prime}}),\quad\mathbf{y}^{{\prime\prime}}\ge g(\mathbf{x}^{{\prime\prime}}).

Zdefiniujmy \mathbf{x}=\lambda\mathbf{x}^{{\prime}}+(1-\lambda)\mathbf{x}^{{\prime\prime}}. Z wypukłości \mathbb{X} wynika, że \mathbf{x}\in\mathbb{X}. Mamy również

\lambda y_{0}^{{\prime}}+(1-\lambda)y_{0}^{{\prime\prime}}\ge\lambda f(\mathbf{x}^{{\prime}})+(1-\lambda)f(\mathbf{x}^{{\prime\prime}})\ge f\big(\lambda\mathbf{x}^{{\prime}}+(1-\lambda)\mathbf{x}^{{\prime\prime}}\big)=f(\mathbf{x}),

gdzie pierwsza nierówność wynika z powyższych własności \mathbf{x}^{{\prime}} i \mathbf{x}^{{\prime\prime}}, zaś druga nierówność z wypukłości f. Podobnie, korzystając z wypukłości g, pokazujemy, że

\lambda\mathbf{y}^{{\prime}}+(1-\lambda)\mathbf{y}^{{\prime\prime}}\ge g(\mathbf{x}).

Stąd {\bar{\mathbf{y}}}=\lambda{\bar{\mathbf{y}}}^{{\prime}}+(1-\lambda){\bar{\mathbf{y}}}^{{\prime\prime}}\in A, ponieważ

y_{0}\ge f(\mathbf{x}),\qquad\mathbf{y}\ge g(\mathbf{x})

dla zdefiniowanego powyżej punktu \mathbf{x}. Kończy to dowód wypukłości zbioru A.

Na mocy słabego twierdzenia o oddzielaniu, tw. 3.1, istnieje \tilde{\mu}\in\mathbb{R}^{{m+1}}, \tilde{\mu}\ne\mathbf{0} i takie że

\tilde{\mu}^{T}{\bar{\mathbf{y}}}\ge\tilde{\mu}^{T}{\bar{\mathbf{z}}},\qquad\forall\ {\bar{\mathbf{y}}}\in A,\ {\bar{\mathbf{z}}}\in C.

Z faktu, że \sup _{{{\bar{\mathbf{z}}}\in C}}\tilde{\mu}^{T}{\bar{\mathbf{z}}}<\infty wynika, że \tilde{\mu}\ge 0. Z ciągłości funkcji liniowej wnioskujemy, że {\bar{\mathbf{z}}} można brać z domknięcia C:

\tilde{\mu}^{T}{\bar{\mathbf{y}}}\ge\tilde{\mu}^{T}{\bar{\mathbf{z}}},\qquad\forall\ {\bar{\mathbf{y}}}\in A,\ {\bar{\mathbf{z}}}\in\mathop{\rm cl}C.

Zatem dla {\bar{\mathbf{z}}}=[f({\bar{\mathbf{x}}}),\mathbf{0}]^{T} mamy

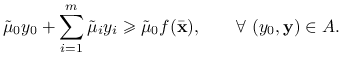\tilde{\mu}_{0}y_{0}+\sum _{{i=1}}^{m}\tilde{\mu}_{i}y_{i}\ge\tilde{\mu}_{0}f({\bar{\mathbf{x}}}),\qquad\forall\ (y_{0},\mathbf{y})\in A.

W szczególności powyższa nierówność zachodzi dla y_{0}=f(\mathbf{x}) i \mathbf{y}=g(\mathbf{x}) dla \mathbf{x}\in\mathbb{X}:

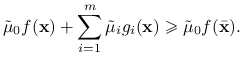\tilde{\mu}_{0}f(\mathbf{x})+\sum _{{i=1}}^{m}\tilde{\mu}_{i}g_{i}(\mathbf{x})\ge\tilde{\mu}_{0}f({\bar{\mathbf{x}}}). (10.2)

Wykażemy teraz, że \tilde{\mu}_{0}\ne 0, co razem z obserwacją \tilde{\mu}\ge 0 będzie implikować \tilde{\mu}_{0}>0. Dowód przeprowadzimy przez zaprzeczenie: załóżmy \tilde{\mu}_{0}=0. Wówczas z nierówności (10.2) wynika, że

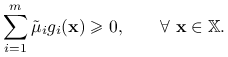\sum _{{i=1}}^{m}\tilde{\mu}_{i}g_{i}(\mathbf{x})\ge 0,\qquad\forall\ \mathbf{x}\in\mathbb{X}.

W szczególności zachodzi to dla punktu \mathbf{x}^{*} z założenia twierdzenia. W tym punkcie mamy jednak g_{i}(\mathbf{x}^{*})<0 dla każdego i=1,\ldots,m. To, w połączeniu z faktem, iż \tilde{\mu}\ge 0 pociąga \tilde{\mu}_{1},\ldots,\tilde{\mu}_{m}=0. Przypomnijmy, że \tilde{\mu}_{0}=0, czyli \tilde{\mu}=\mathbf{0}, a to przeczy wyborowi \tilde{\mu} z twierdzenia o oddzielaniu.

Wiemy zatem, że \tilde{\mu}_{0}>0. Zdefiniujmy

{\bar{\mu}}=\Big[\frac{\tilde{\mu}_{1}}{\tilde{\mu}_{0}},\ldots,\frac{\tilde{\mu}_{m}}{\tilde{\mu}_{0}}\Big]^{T}.

Oczywiście {\bar{\mu}}\in[0,\infty)^{m}. Ponieważ {\bar{\mathbf{x}}}, jako rozwiązanie, jest punktem dopuszczalnym, to g_{i}({\bar{\mathbf{x}}})\le 0, i=1,\ldots,m, i \sum _{{i=1}}^{m}{\bar{\mu}}_{i}g_{i}({\bar{\mathbf{x}}})\le 0. Dodajemy tą sumę do prawej strony nierówności (10.2) podzielonej przez \tilde{\mu}_{0}:

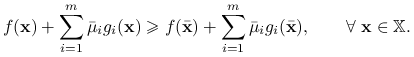f(\mathbf{x})+\sum _{{i=1}}^{m}{\bar{\mu}}_{i}g_{i}(\mathbf{x})\ge f({\bar{\mathbf{x}}})+\sum _{{i=1}}^{m}{\bar{\mu}}_{i}g_{i}({\bar{\mathbf{x}}}),\qquad\forall\ \mathbf{x}\in\mathbb{X}.

Inaczej,

L(\mathbf{x},{\bar{\mu}})\ge L({\bar{\mathbf{x}}},{\bar{\mu}}),\qquad\forall\ \mathbf{x}\in\mathbb{X}.

Pozostaje jeszcze wykazanie drugiej nierówności punktu siodłowego. Biorąc \mathbf{x}={\bar{\mathbf{x}}} i dzieląc obie strony nierówności (10.2) przez \tilde{\mu}_{0} dostajemy \sum _{{i=1}}^{m}{\bar{\mu}}_{i}g_{i}({\bar{\mathbf{x}}})\ge 0. Z drugiej strony punkt {\bar{\mathbf{x}}} jest dopuszczalny, czyli g_{i}({\bar{\mathbf{x}}})\le 0. Pamiętając, że {\bar{\mu}}\ge 0 wnioskujemy, że każdy składnik tej sumy jest niedodatni. Stąd już mamy

{\bar{\mu}}_{i}g_{i}({\bar{\mathbf{x}}})=0,\qquad i=1,\ldots,m.

Dla dowolnego innego \mu\in[0,\infty)^{m} mamy \sum _{{i=1}}^{m}\mu _{i}g_{i}({\bar{\mathbf{x}}})\le 0, czyli

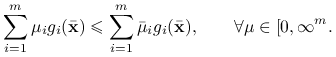\sum _{{i=1}}^{m}\mu _{i}g_{i}({\bar{\mathbf{x}}})\le\sum _{{i=1}}^{m}{\bar{\mu}}_{i}g_{i}({\bar{\mathbf{x}}}),\qquad\forall\mu\in[0,\infty^{m}.

Ta nierówność jest równoważna

L({\bar{\mathbf{x}}},\mu)\le L({\bar{\mathbf{x}}},{\bar{\mu}}),\qquad\forall\ \mu\in[0,\infty)^{m}.
∎

10.3. Zadanie pierwotne i dualne

Z teorią puntów siodłowych związane są pojęcia zadania pierwotnego i dualnego. Rozważmy zadanie optymalizacyjne (10.1) i związaną z nim funkcję Lagrange'a L(\mathbf{x},\mu). Zdefiniujmy funkcję L_{P}:\mathbb{X}\to(-\infty,\infty]

L_{P}(\mathbf{x})=\sup _{{\mu\in[0,\infty)^{m}}}L(\mathbf{x},\mu).

Zauważmy, że

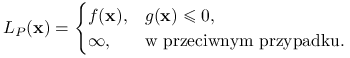L_{P}(\mathbf{x})=\begin{cases}f(\mathbf{x}),&g(\mathbf{x})\le 0,\\ \infty,&\text{w przeciwnym przypadku.}\end{cases}

A zatem zadanie (10.1) można zapisać w wydawałoby się prostszej postaci

L_{P}(\mathbf{x})\to\min,\qquad\mathbf{x}\in\mathbb{X}.

Niestety powyższe przeformułowanie sprowadza się do rozwiązania oryginalnego zadania, a więc nie zawiera żadnej ,,wartości dodanej”; ale tylko do czasu. Zanim zdradzimy jego zastosowanie, zdefiniujmy kolejną funkcję L_{D}:[0,\infty)^{m}\to[-\infty,\infty)

L_{D}(\mu)=\inf _{{\mathbf{x}\in\mathbb{X}}}L(\mathbf{x},\mu).
Uwaga 10.4

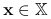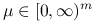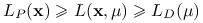  1. Dla dowolnego \mathbf{x}\in\mathbb{X} i \mu\in[0,\infty)^{m} mamy L_{P}(\mathbf{x})\ge L(\mathbf{x},\mu)\ge L_{D}(\mu).

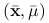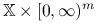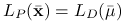  2. Jeśli ({\bar{\mathbf{x}}},{\bar{\mu}}) jest punktem siodłowym funkcji Lagrange'a na \mathbb{X}\times[0,\infty)^{m}, to L_{P}({\bar{\mathbf{x}}})=L_{D}({\bar{\mu}}).

Powyższe spostrzeżenia kierują nas we właściwą stronę. Będziemy wykorzystywać funkcje L_{P} i L_{D} do znajdowania punktów siodłowych.

Definicja 10.2

Zadaniem pierwotnym nazywamy problem optymalizacyjny

L_{P}(\mathbf{x})\to\min,\qquad\mathbf{x}\in\mathbb{X}.

Zadaniem dualnym do niego jest problem optymalizacyjny

L_{D}(\mu)\to\max,\qquad\mu\in[0,\infty)^{m}.

Z własności wspomnianych w uwadze 10.4 wynika, że wartość rozwiązania zadania pierwotnego jest nie mniejsza niż wartość rozwiązania zadania dualnego:

\inf _{{\mathbf{x}\in\mathbb{X}}}L_{P}(\mathbf{x})\ge\sup _{{\mu\in[0,\infty)^{m}}}L_{D}(\mu).

Co więcej, rozwiązanie zadania dualnego daje dolne oszacowanie na wartość funkcji f:

Lemat 10.2 (Słabe twierdzenie o dualności)

Dla dowolnego punktu dopuszczalnego \mathbf{x}\in W oraz dowolnego \mu\in[0,\infty)^{m} mamy

f(\mathbf{x})\ge L_{D}(\mu).

A zatem

f(\mathbf{x})\ge\sup _{{\mu\in[0,\infty)^{m}}}L_{D}(\mu).
Dowód

Dowód pozostawiamy jako ćwiczenie.

∎
Definicja 10.3

Luką dualności nazwiemy różnicę między wartością rozwiązania zadania pierwotnego i dualnego:

\inf _{{\mathbf{x}\in\mathbb{X}}}L_{P}(\mathbf{x})-\sup _{{\mu\in[0,\infty)^{m}}}L_{D}(\mu).

Zapiszmy w języku funkcji pierwotnej i dualnej warunek punktu siodłowego: ({\bar{\mathbf{x}}},\bar{\mu}) jest punktem siodłowym, jeśli

L_{P}({\bar{\mathbf{x}}})=L({\bar{\mathbf{x}}},\bar{\mu})=L_{D}(\bar{\mu}).

Innymi słowy, jeśli funkcja Lagrange'a posiada punkt siodłowy, to luka dualności jest zerowa. Ma to miejsce, na przykład, jeśli spełnione są założenia tw. 10.2.

Możemy teraz zaproponować algorytm rozwiązywania zagadnienia (10.1) przy pomocy metod dualnych.

  1. Rozwiąż zadanie dualne. Jego wartość daje dolne ograniczenie na wartość rozwiązania problemu pierwotnego na mocy lematu 10.2.

  2. Załóżmy, że istnieje rozwiązanie skończone {\bar{\mu}}\in[0,\infty) zadania dualnego oraz taki punkt {\bar{\mathbf{x}}}\in\mathbb{X}, że L_{D}({\bar{\mu}})=L({\bar{\mathbf{x}}},{\bar{\mu}}). Jeśli {\bar{\mathbf{x}}} jest dopuszczalny oraz f({\bar{\mathbf{x}}})=L_{D}({\bar{\mu}}), to ({\bar{\mathbf{x}}},{\bar{\mu}}) jest punktem siodłowym funkcji Lagrange'a i twierdzenie 10.1 implikuje, że {\bar{\mathbf{x}}} jest rozwiązaniem zadania (10.1).

Wyjaśnijmy warunki punktu drugiego. Z faktu L_{D}({\bar{\mu}})=L({\bar{\mathbf{x}}},{\bar{\mu}}) wynika, że L({\bar{\mathbf{x}}},{\bar{\mu}})\le L(\mathbf{x},{\bar{\mu}}) dla dowolnego \mathbf{x}\in\mathbb{X}. Zatem mamy prawą nierówność warunku punktu siodłowego. Pozostaje jeszcze nierówność lewa. Przypomnijmy, że L_{P}(\mathbf{x})=f(\mathbf{x}) dla punktu dopuszczalnego \mathbf{x} i \inf _{{\mathbf{x}\in\mathbb{X}}}L_{P}(\mathbf{x})\ge L_{D}(\mu) dla dowolnego \mu\in[0,\infty)^{m}. W punkcie drugim zakładamy, że f({\bar{\mathbf{x}}})=L_{D}({\bar{\mu}}), co pociąga

L_{P}({\bar{\mathbf{x}}})=f({\bar{\mathbf{x}}})=L_{D}({\bar{\mu}}),

a zatem ({\bar{\mathbf{x}}},{\bar{\mu}}) jest punktem siodłowym.

10.4. Zadania

Ćwiczenie 10.1

Udowodnij, że jeśli w problemie optymalizacyjnym (10.1) funkcje f i g_{i}, i=1,\ldots,m, są wypukłe, to punkt spełniający warunek konieczny pierwszego rzędu jest punktem siodłowym funkcji Lagrange'a na przestrzeni \mathbb{X}\times[0,\infty)^{m}.

Ćwiczenie 10.2

Uzasadnij, że L_{P}(\mathbf{x})\ge L(\mathbf{x},\mu)\ge L_{D}(\mu) dla dowolnego \mathbf{x}\in\mathbb{X} i \mu\in[0,\infty)^{m}.

Ćwiczenie 10.3

Uzasadnij nierówność:

\inf _{{\mathbf{x}\in\mathbb{X}}}L_{P}(\mathbf{x})\ge\sup _{{\mu\in[0,\infty)^{m}}}L_{D}(\mu).
Ćwiczenie 10.4

Udowodnij, że jeśli ({\bar{\mathbf{x}}},{\bar{\mu}}) jest punktem siodłowym funkcji Lagrange'a, to L_{P}({\bar{\mathbf{x}}})=L_{D}({\bar{\mu}}) lub, innymi słowy, luka dualności jest zerowa.

Ćwiczenie 10.5

Udowodnij lemat 10.2.

Ćwiczenie 10.6

Wykaż, że funkcja dualna L_{D} jest wklęsła.

Ćwiczenie 10.7

Podaj przykład problemu optymalizacyjnego, dla którego luka dualności jest dodatnia.

Ćwiczenie 10.8

Rozwiąż metodą dualną zadanie

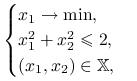\begin{cases}x_{1}\to\min,&\\ x_{1}^{2}+x_{2}^{2}\le 2,&\\ (x_{1},x_{2})\in\mathbb{X},&\end{cases}

gdzie \mathbb{X}=\{\mathbf{x}\in\mathbb{R}^{2}:\ x_{1}\ge 1\}. Zwróć uwagę na umieszczenie jednego z ograniczeń w zbiorze \mathbb{X}.

Ćwiczenie 10.9

Rozwiąż metodą dualną zadanie

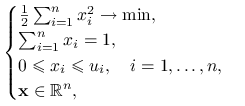\begin{cases}\frac{1}{2}\sum _{{i=1}}^{n}x_{i}^{2}\to\min,&\\ \sum _{{i=1}}^{n}x_{i}=1,&\\ 0\le x_{i}\le u_{i},\quad i=1,\ldots,n,&\\ \mathbf{x}\in\mathbb{R}^{n},&\end{cases}

gdzie 0\le u_{1}\le\ldots\le u_{n} oraz \sum _{{i=1}}^{n}u_{i}\ge 1.

Wskazówka: 

Rozważ zbiór \mathbb{X}=\{\mathbf{x}\in\mathbb{R}^{n}:\ 0\le x_{i}\le u_{i}\text{ dla $i=1,\ldots,n$}\}.

Ćwiczenie 10.10

Znajdź zadanie dualne (czyli formę zadania \sup _{{\mu\in[0,\infty)^{m}}}L_{D}(\mu)) dla zadania optymalizacji liniowej

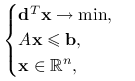\begin{cases}\mathbf{d}^{T}\mathbf{x}\to\min,&\\ A\mathbf{x}\le\mathbf{b},&\\ \mathbf{x}\in\mathbb{R}^{n},&\end{cases}

gdzie \mathbf{d}\in\mathbb{R}^{n}, A jest macierzą m\times n i \mathbf{b}\in\mathbb{R}^{m}.

Ćwiczenie 10.11

Znajdź zadanie dualne do zadania programowania kwadratowego

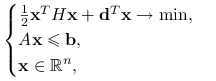\begin{cases}\frac{1}{2}\mathbf{x}^{T}H\mathbf{x}+\mathbf{d}^{T}\mathbf{x}\to\min,&\\ A\mathbf{x}\le\mathbf{b},&\\ \mathbf{x}\in\mathbb{R}^{n},&\end{cases}

gdzie H jest macierzą symetryczną dodatnio określoną, \mathbf{d}\in\mathbb{R}^{n}, A jest macierzą m\times n i \mathbf{b}\in\mathbb{R}^{m}.

Definicja 10.4

Niech \mathbb{X}\subset\mathbb{R}^{n}. Transformatą Legendre'a-Fenchela funkcji f:\mathbb{X}\to\mathbb{R} nazywamy funkcję f^{*}:\mathbb{R}^{n}\to\mathbb{R}\cup\{+\infty\} daną wzorem

f^{*}(\mathbf{y})=\sup _{{\mathbf{x}\in\mathbb{X}}}\big(\mathbf{y}^{T}\mathbf{x}-f(\mathbf{x})\big).
Ćwiczenie 10.12

Rozważmy problem optymalizacyjny:

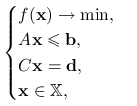\begin{cases}f(\mathbf{x})\to\min,&\\ A\mathbf{x}\le\mathbf{b},&\\ C\mathbf{x}=\mathbf{d},&\\ \mathbf{x}\in\mathbb{X},&\end{cases}

gdzie \mathbb{X}\subset\mathbb{R}^{n}, \mathbf{b}\in\mathbb{R}^{m}, \mathbf{d}\in\mathbb{R}^{l}, zaś A,C są dowolnymi macierzami o odpowiednich wymiarach. Udowodnij, że problem do niego dualny ma następującą postać:

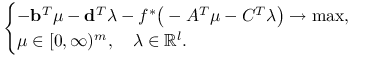\begin{cases}-\mathbf{b}^{T}\mu-\mathbf{d}^{T}\lambda-f^{*}\big(-A^{T}\mu-C^{T}\lambda\big)\to\max,&\\ \mu\in[0,\infty)^{m},\quad\lambda\in\mathbb{R}^{l}.&\end{cases}
Wskazówka: 

Rozbij ograniczenie równościowe na dwa ograniczenia nierównościowe.

Ćwiczenie 10.13

Znajdź transformatę Legendre'a-Fenchela następujących funkcji:

\displaystyle f(x)=\frac{1}{2}x^{2},\qquad x\in\mathbb{X}=\mathbb{R},
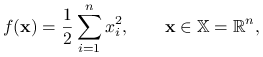\displaystyle f(\mathbf{x})=\frac{1}{2}\sum _{{i=1}}^{n}x_{i}^{2},\qquad\mathbf{x}\in\mathbb{X}=\mathbb{R}^{n},
\displaystyle f(x)=e^{x},\qquad x\in\mathbb{X}=\mathbb{R},
\displaystyle f(\mathbf{x})=\|\mathbf{x}\| _{p},\qquad\mathbf{x}\in\mathbb{X}=\mathbb{R}^{n},\quad p>1,
\displaystyle f(\mathbf{x})=\frac{1}{2}\mathbf{x}^{T}H\mathbf{x},\qquad\mathbf{x}\in\mathbb{X}=\mathbb{R}^{n},\quad\text{$H$ - macierz symetryczna, nieosobliwa.}
Ćwiczenie 10.14

Udowodnij, że transformata Legendre'a-Fenchela f^{*} jest wypukła dla dowolnej funkcji f.

Ćwiczenie 10.15

Wykaż równoważność następujących dwóch zadań optymalizacyjnych:

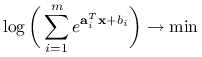\log\bigg(\sum _{{i=1}}^{m}e^{{\mathbf{a}_{i}^{T}\mathbf{x}+b_{i}}}\bigg)\to\min

oraz

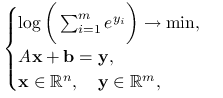\begin{cases}\log\bigg(\sum _{{i=1}}^{m}e^{{y_{i}}}\bigg)\to\min,&\\ A\mathbf{x}+\mathbf{b}=\mathbf{y},&\\ \mathbf{x}\in\mathbb{R}^{n},\quad\mathbf{y}\in\mathbb{R}^{m},&\end{cases} (10.3)

gdzie przez \mathbf{a}_{1},\ldots,\mathbf{a}_{m} oznaczamy rzędy macierzy A. Udowodnij następnie, że zadaniem dualnym do (10.3) jest

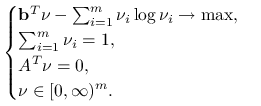\begin{cases}\mathbf{b}^{T}\nu-\sum _{{i=1}}^{m}\nu _{i}\log\nu _{i}\to\max,&\\ \sum _{{i=1}}^{m}\nu _{i}=1,&\\ A^{T}\nu=0,&\\ \nu\in[0,\infty)^{m}.&\end{cases}
« 9. Warunki drugiego rzędu  Spis treści  11. Teoria wrażliwości »  

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

strona główna | webmaster | o portalu | pomoc

© Wydział Matematyki, Informatyki i Mechaniki UW, 2009-2010. Niniejsze materiały są udostępnione bezpłatnie na licencji Creative Commons Uznanie autorstwa-Użycie niekomercyjne-Bez utworów zależnych 3.0 Polska.

Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego.

Projekt współfinansowany przez Ministerstwo Nauki i Szkolnictwa Wyższego i przez Uniwersytet Warszawski.