Zagadnienia
7. Funkcje quasi-wypukłe i warunki dostateczne
Mogliśmy już zaobserwować na kilku przykładach, że wypukłość znacznie ułatwia rozwiązywanie problemów optymalizacyjnych. W rozdziale 3 zauważyliśmy, że warunkiem koniecznym i dostatecznym minimum funkcji wypukłej jest zerowanie się pochodnej. Później wykazaliśmy, że identyczny warunek zachodzi dla większej rodziny funkcji: funkcji pseudowypukłych. W rozdziale 4 zajmowaliśmy się maksymalizacją funkcji wypukłej na zbiorze wypukłym i zwartym. Udowodniliśmy, że maksimum jest przyjmowane w jednym z punktów ekstremalnych tego zbioru. W tym rozdziale rozszerzymy rodzinę funkcji, dla których jest to prawdą; wprowadzimy własność quasi-wypukłości.
Patrząc na powyższą listę można się domyślać, że wypukłość może również pomagać przy rozwiązywaniu zadań z ograniczeniami nierównościowymi. Jeśli założymy, że funkcje ![]() , opisujące ograniczenia nierównościowe, są wypukłe lub, ogólniej, quasi-wypukłe oraz funkcja
, opisujące ograniczenia nierównościowe, są wypukłe lub, ogólniej, quasi-wypukłe oraz funkcja ![]() jest pseudowypukła, to spełnienie warunku pierwszego rzędu w pewnym punkcie
jest pseudowypukła, to spełnienie warunku pierwszego rzędu w pewnym punkcie ![]() jest wystarczające, by stwierdzić jego optymalność. Dowód powyższego faktu przytoczymy pod koniec tego rozdziału.
jest wystarczające, by stwierdzić jego optymalność. Dowód powyższego faktu przytoczymy pod koniec tego rozdziału.
7.1. Quasi-wypukłość
W tym podrozdziale rozszerzymy rodzinę funkcji, dla których maksimum znajduje się w punktach ekstremalnych dziedziny.
Definicja 7.1
Niech ![]() będzie zbiorem wypukłym, zaś
będzie zbiorem wypukłym, zaś ![]() .
.
Funkcję ![]() nazywamy quasi-wypukłą, jeśli dla dowolnych
nazywamy quasi-wypukłą, jeśli dla dowolnych ![]() i
i ![]() mamy
mamy
Funkcję ![]() nazywamy quasi-wklęsłą, jeśli funkcja
nazywamy quasi-wklęsłą, jeśli funkcja ![]() jest quasi-wypukła, tzn. dla dowolnych
jest quasi-wypukła, tzn. dla dowolnych ![]() i
i ![]() zachodzi
zachodzi
Funkcję ![]() nazywamy quasi-liniową, jeśli jest ona jednocześnie quasi-wypukła i quasi-wklęsła.
nazywamy quasi-liniową, jeśli jest ona jednocześnie quasi-wypukła i quasi-wklęsła.
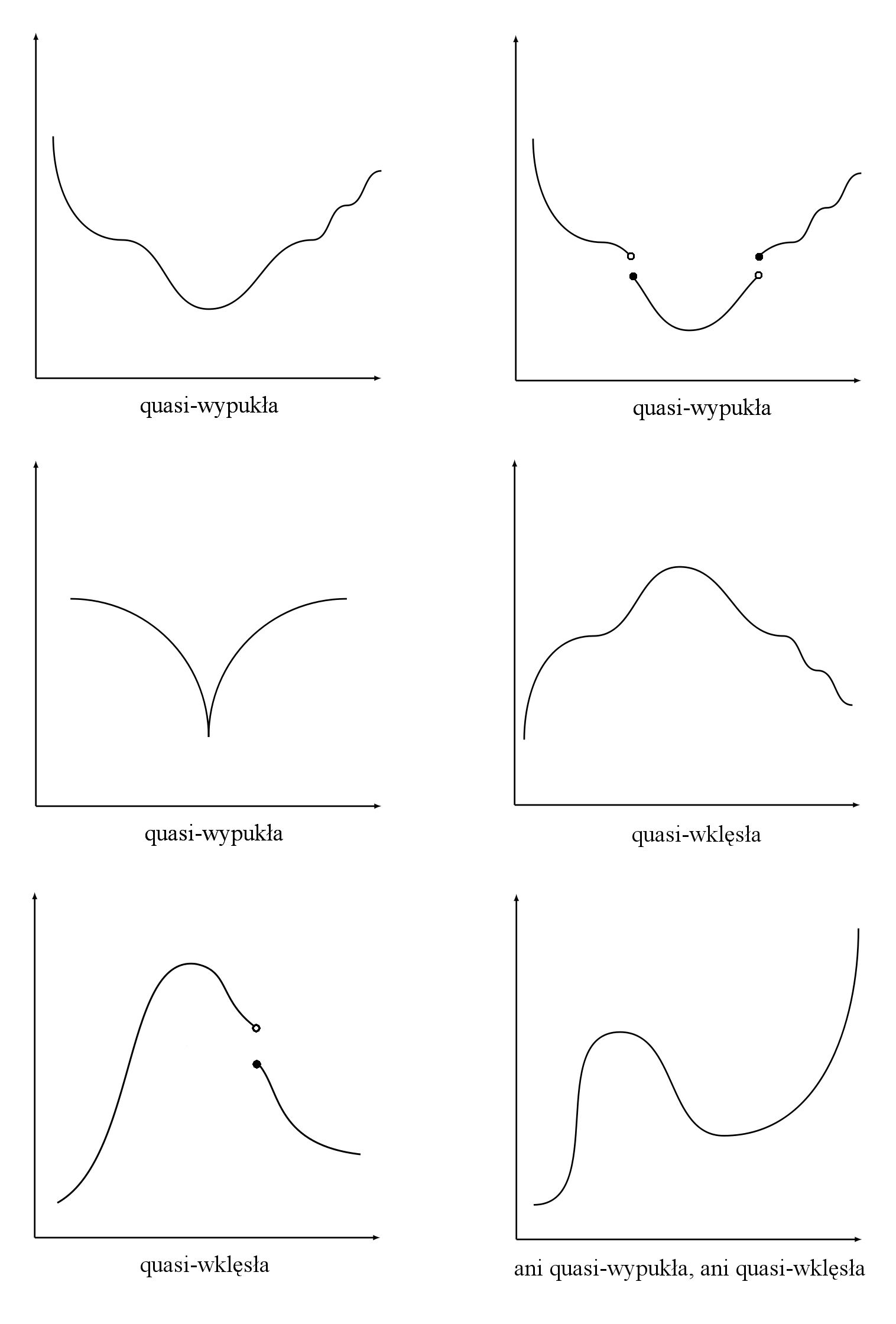
Na rys. 7.1 pokazane są przykłady jednowymiarowych funkcji quasi-wypukłych i quasi-wklęsłych. Zwróćmy uwagę na to, że funkcje takie nie muszą być ciągłe, nie mówiąc już o różniczkowalności. Ciekawym jest również uogólnienie rodziny funkcji afinicznych do funkcji quasi-liniowych, patrz rys. 7.2.
Przykład 7.1
Funkcja afiniczna jest quasi-liniowa. Rzeczywiście, niech ![]() dla
dla ![]() i
i ![]() . Wówczas dla dowolnych
. Wówczas dla dowolnych ![]() i
i ![]() mamy
mamy
Prawa strona jest oczywiście nie mniejsza od minimum z ![]() i
i ![]() i nie większa od maksimum tych liczb, czyli
i nie większa od maksimum tych liczb, czyli ![]() jest zarówno quasi-wypukła jak i quasi-wklęsła.
jest zarówno quasi-wypukła jak i quasi-wklęsła.
Przypomnijmy, że zbiorem poziomicowym funkcji ![]() nazywamy zbiór
nazywamy zbiór
Twierdzenie 7.1
Niech ![]() , gdzie
, gdzie ![]() wypukły. Wówczas funkcja
wypukły. Wówczas funkcja ![]() jest quasi-wypukła wtw, gdy zbiór poziomicowy
jest quasi-wypukła wtw, gdy zbiór poziomicowy ![]() jest wypukły dla każdego
jest wypukły dla każdego ![]() .
.
Dowód
Załóżmy, że funkcja ![]() jest quasi-wypukła i ustalmy
jest quasi-wypukła i ustalmy ![]() . Niech
. Niech ![]() . Wówczas
. Wówczas ![]() i
i ![]() . Dla dowolnego
. Dla dowolnego ![]() dostajemy
dostajemy
Wnioskujemy stąd, że ![]() , czyli
, czyli ![]() jest zbiorem wypukłym.
jest zbiorem wypukłym.
Załóżmy teraz, że ![]() jest wypukły dla każdego
jest wypukły dla każdego ![]() . Ustalmy
. Ustalmy ![]() oraz
oraz ![]() . Na mocy założenia zbiór
. Na mocy założenia zbiór ![]() jest wypukły dla
jest wypukły dla ![]() Wynika stąd, że
Wynika stąd, że ![]() , czyli
, czyli
Uwaga 7.1
Analogiczne twierdzenie dla funkcji wypukłej, tw. 3.5, brzmiało: funkcja ![]() jest wypukła wtw, gdy jej epigraf jest zbiorem wypukłym.
jest wypukła wtw, gdy jej epigraf jest zbiorem wypukłym.
Wniosek 7.1
Funkcja wypukła jest quasi-wypukła.
Twierdzenie przeciwne nie jest prawdziwe. Poniżej podajemy przykład funkcji quasi-wypukłej, która nie jest wypukła.
Przykład 7.2
Funkcja ![]() , dla
, dla ![]() , jest quasi-wypukła choć jest ściśle wklęsła. Dla
, jest quasi-wypukła choć jest ściśle wklęsła. Dla ![]() zbiór
zbiór ![]() , zaś dla
, zaś dla ![]() mamy
mamy ![]() . Wszystkie te zbiory są wypukłe, więc na mocy twierdzenia 7.1 funkcja
. Wszystkie te zbiory są wypukłe, więc na mocy twierdzenia 7.1 funkcja ![]() jest quasi-wypukła. W podobny sposób możemy także pokazać, że funkcja
jest quasi-wypukła. W podobny sposób możemy także pokazać, że funkcja ![]() jest quasi-wklęsła, a zatem quasi-liniowa.
jest quasi-wklęsła, a zatem quasi-liniowa.
Przykład 7.3
Funkcja ![]() ,
, ![]() , jest ściśle wklęsła a zarazem quasi-liniowa (czyli, między innymi, quasi-wypukła).
, jest ściśle wklęsła a zarazem quasi-liniowa (czyli, między innymi, quasi-wypukła).
Przykład 7.4
Funkcja ![]() jest quasi-wypukła, lecz nie jest quasi-wklęsła. Quasi-wypukłość wynika z wypukłości
jest quasi-wypukła, lecz nie jest quasi-wklęsła. Quasi-wypukłość wynika z wypukłości ![]() . Quasi-wklęsłość badamy rozpatrując zbiory poziomicowe funkcji
. Quasi-wklęsłość badamy rozpatrując zbiory poziomicowe funkcji ![]() . Dla
. Dla ![]() mamy
mamy ![]() . Nie jest to zbiór wypukły, czyli funkcja
. Nie jest to zbiór wypukły, czyli funkcja ![]() nie jest quasi-wypukła.
nie jest quasi-wypukła.
Dowód poniższego lematu pozostawiamy jako zadanie.
Lemat 7.1
Funkcja ![]() ,
, ![]() wypukły, jest quasi-liniowa wtw, gdy jej obcięcie do dowolnego odcinka jest funkcją monotoniczną.
wypukły, jest quasi-liniowa wtw, gdy jej obcięcie do dowolnego odcinka jest funkcją monotoniczną.
Na mocy tego lematu możemy od razu zauważyć, że funkcja z przykładu 7.2 jest quasi-liniowa.
Okazuje się, że istnieją funkcje quasi-wypukłe jednej zmiennej, które nie są ani wypukłe ani monotoniczne.
Przykład 7.5
Funkcja ![]() jest quasi-wypukła. Mamy następujące zbiory poziomicowe w zależności od
jest quasi-wypukła. Mamy następujące zbiory poziomicowe w zależności od ![]() :
:
Wszystkie te zbiory są wypukłe, czyli na mocy tw. 7.1 funkcja ![]() jest quasi-wypukła.
jest quasi-wypukła.
Na koniec podamy przykład funkcji quasi-wypukłej wielu zmiennych, która nie jest wypukła.
Przykład 7.6
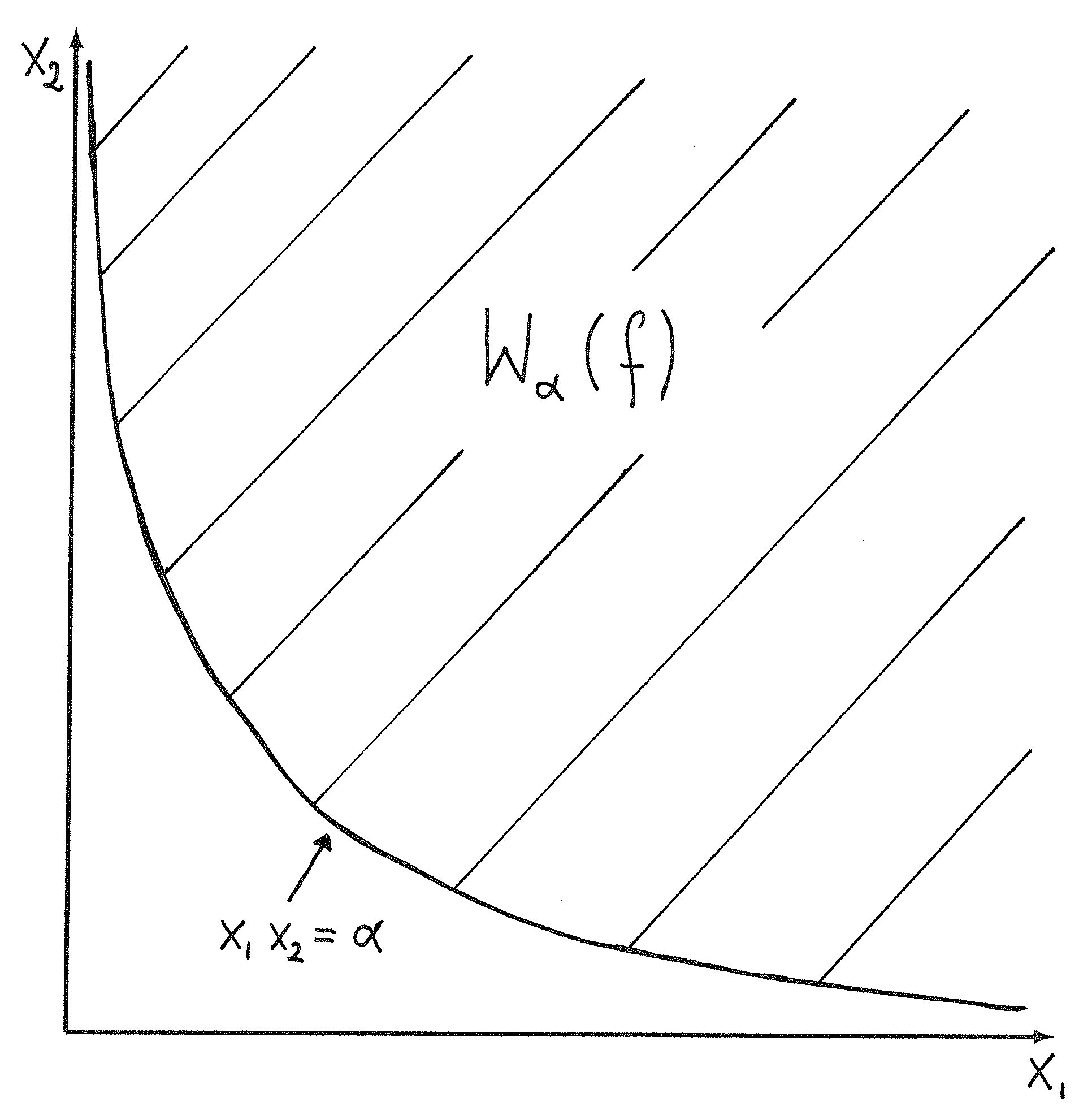
Funkcja ![]() zadana wzorem
zadana wzorem ![]() jest quasi-wypukła. Jej zbiory poziomicowe dla
jest quasi-wypukła. Jej zbiory poziomicowe dla ![]() są trywialne:
są trywialne: ![]() , zaś dla
, zaś dla ![]() mają formę przedstawioną na rysunku 7.3. Funkcja
mają formę przedstawioną na rysunku 7.3. Funkcja ![]() nie jest ani wypukła ani wklęsła, gdyż jej hesjan ma wartości własne
nie jest ani wypukła ani wklęsła, gdyż jej hesjan ma wartości własne ![]() i
i ![]()
Przykład 7.7
Niech ![]() i
i ![]() . Połóżmy
. Połóżmy ![]() Wówczas funkcja wymierna
Wówczas funkcja wymierna ![]()
jest quasi-liniowa. Dowód pozostawiamy jako ćwiczenie.
Zbadamy teraz własności różniczkowalnych funkcji quasi-wypukłych.
Twierdzenie 7.2
Niech ![]() dla wypukłego zbioru
dla wypukłego zbioru ![]() .
.
I) Jeśli funkcja
 jest quasi-wypukła i różniczkowalna w
jest quasi-wypukła i różniczkowalna w 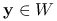 , to
, to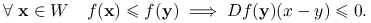
II) Załóżmy, że funkcja
 jest różniczkowalna w każdym punkcie
jest różniczkowalna w każdym punkcie 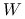 . Wówczas
. Wówczas  jest quasi-wypukła wtw, gdy zachodzi następujący warunek:
jest quasi-wypukła wtw, gdy zachodzi następujący warunek: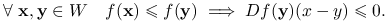
Uwaga 7.2
Implikacja
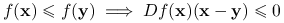 ma równoważną postać:
ma równoważną postać: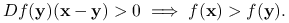
Jeśli funkcja
 jest quasi-liniowa i
jest quasi-liniowa i 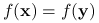 , to
, to 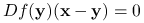 .
.
Dowód tw. 7.2
(I): Ustalmy ![]() , dla których zachodzi warunek
, dla których zachodzi warunek ![]() . Dla każdego
. Dla każdego ![]() mamy
mamy
Wynika stąd, że
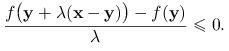 |
Z definicji pochodnej kierunkowej dostajemy
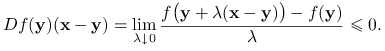 |
Dowód (II) pozostawiamy jako niełatwe ćwiczenie.
∎Wiemy już, że funkcja wypukła jest quasi-wypukła. Okazuje się, że również funkcja pseudowypukła jest quasi-wypukła.
Twierdzenie 7.3
Jeśli ![]() określona na zbiorze wypukłym
określona na zbiorze wypukłym ![]() jest pseudowypukła, to
jest pseudowypukła, to ![]() jest quasi-wypukła.
jest quasi-wypukła.
Dowód
Zakładając, że funkcja ![]() nie jest quasi-wypukła doprowadzimy do sprzeczności z pseudowypukłością. Weźmy więc punkty
nie jest quasi-wypukła doprowadzimy do sprzeczności z pseudowypukłością. Weźmy więc punkty ![]() oraz
oraz ![]() spełniające
spełniające
Oznaczmy ![]() . Na mocy pseudowypukłości (wykorzystujemy tu warunek pseudowypukłości zapisany w uwadze 4.3) dostajemy:
. Na mocy pseudowypukłości (wykorzystujemy tu warunek pseudowypukłości zapisany w uwadze 4.3) dostajemy:
Wektory ![]() i
i ![]() mają ten sam kierunek lecz przeciwne zwroty. Pochodna
mają ten sam kierunek lecz przeciwne zwroty. Pochodna ![]() w punkcie
w punkcie ![]() nie może być ujemna w obu kierunkach. Sprzeczność.
nie może być ujemna w obu kierunkach. Sprzeczność.
Twierdzenie odwrotne nie jest prawdziwe. Możemy jednak podać warunek dostateczny, przy którym funkcja quasi-wypukła jest pseudowypukła.
Twierdzenie 7.4
Niech ![]() określona na zbiorze wypukłym otwartym
określona na zbiorze wypukłym otwartym ![]() będzie quasi-wypukła i ciągła. Jeśli
będzie quasi-wypukła i ciągła. Jeśli ![]() jest różniczkowalna w
jest różniczkowalna w ![]() oraz
oraz ![]() , to
, to ![]() jest pseudowypukła w
jest pseudowypukła w ![]() .
.
Dowód
Musimy pokazać, że dla każdego ![]() warunek
warunek ![]() pociąga
pociąga ![]() . Oznaczmy przez
. Oznaczmy przez ![]() przestrzeń afiniczną prostopadłą do
przestrzeń afiniczną prostopadłą do ![]() i przechodzącą przez
i przechodzącą przez ![]() :
:
Z warunku, że ![]() wynika, że przestrzeń
wynika, że przestrzeń ![]() ma wymiar
ma wymiar ![]() , czyli jest właściwą hiperpłaszczyzną w
, czyli jest właściwą hiperpłaszczyzną w ![]() .
.
Zauważmy najpierw, że jeśli ![]() i
i ![]() , to pochodna kierunkowa jest ściśle dodatnia:
, to pochodna kierunkowa jest ściśle dodatnia: ![]() . Na mocy uwagi 7.2 wnioskujemy, że
. Na mocy uwagi 7.2 wnioskujemy, że ![]() , czyli to, co mieliśmy wykazać. Ustalmy teraz punkt
, czyli to, co mieliśmy wykazać. Ustalmy teraz punkt ![]() . Z otwartości
. Z otwartości ![]() i z tego, że
i z tego, że ![]() jest hiperpłaszczyzną wynika, że istnieje ciąg punktów
jest hiperpłaszczyzną wynika, że istnieje ciąg punktów ![]() zmierzający do
zmierzający do ![]() i taki że
i taki że ![]() . Zatem
. Zatem ![]() . Korzystając z ciągłości funkcji
. Korzystając z ciągłości funkcji ![]() dostajemy
dostajemy ![]() .
.
7.2. Maksymalizacja funkcji quasi-wypukłej
Jak zostało zasygnalizowane wcześniej, funkcja quasi-wypukła zachowuje się podobnie jak funkcja wypukła przy maksymalizacji na zbiorze wypukłym zwartym. Dla pełności przytoczymy dowód, który jest prawie identyczny jak dowód twierdzenia 4.5.
Twierdzenie 7.5
Niech ![]() quasi-wypukła, ciągła, określona na wypukłym i zwartym zbiorze
quasi-wypukła, ciągła, określona na wypukłym i zwartym zbiorze ![]() . Wówczas punkt ekstremalny zbioru
. Wówczas punkt ekstremalny zbioru ![]() jest jednym z rozwiązań globalnych problemu
jest jednym z rozwiązań globalnych problemu
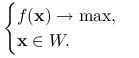 |
Dowód
Funkcja ciągła osiąga swoje kresy na zbiorze zwartym. Powyższy problem maksymalizacyjny ma zatem rozwiązanie ![]() . Na mocy tw. 4.4 punkt
. Na mocy tw. 4.4 punkt ![]() jest kombinacją wypukłą skończonej liczby punktów ekstremalnych,
jest kombinacją wypukłą skończonej liczby punktów ekstremalnych, ![]() , zbioru
, zbioru ![]() , tzn.
, tzn.
dla liczb ![]() takich że
takich że ![]() . Z quasi-wypukłości
. Z quasi-wypukłości ![]() dostajemy
dostajemy
Ponieważ w punkcie ![]() jest maksimum
jest maksimum ![]() na zbiorze
na zbiorze ![]() , to dla któregoś z punktów
, to dla któregoś z punktów ![]() zachodzi równość
zachodzi równość ![]()
7.3. Warunki dostateczne
Zajmiemy się problemem optymalizacyjnym, w którym występują zarówno ograniczenia nierównościowe jak i równościowe:
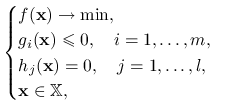 |
(7.1) |
gdzie ![]() jest zbiorem otwartym i
jest zbiorem otwartym i ![]() . A zatem zbiór punktów dopuszczalnych zadany jest następująco:
. A zatem zbiór punktów dopuszczalnych zadany jest następująco:
| (7.2) |
Funkcje ![]() nazywane są ograniczeniami nierównościowymi, funkcje
nazywane są ograniczeniami nierównościowymi, funkcje ![]() są ograniczeniami równościowymi, zaś cały problem (7.1) nazywa się zadaniem optymalizacyjnym z ograniczeniami mieszanymi.
są ograniczeniami równościowymi, zaś cały problem (7.1) nazywa się zadaniem optymalizacyjnym z ograniczeniami mieszanymi.
Podamy teraz warunki dostateczne, by punkt spełniający warunki pierwszego rzędu był rozwiązaniem globalnym.
Twierdzenie 7.6
Rozważmy problem optymalizacyjny w kanonicznej formie (7.1) i punkt ![]() . Załóżmy, że
. Załóżmy, że
funkcje
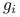 ,
, 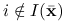 są ciągłe w
są ciągłe w  , funkcje
, funkcje 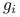 ,
, 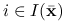 są różniczkowalne w
są różniczkowalne w  i quasi-wypukłe,
i quasi-wypukłe,funkcje
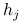 ,
, 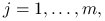 są quasi-liniowe i różniczkowalne w
są quasi-liniowe i różniczkowalne w  ,
,funkcja
 jest pseudowypukła w
jest pseudowypukła w  .
.
Jeśli istnieją stałe ![]() oraz
oraz ![]() spełniające warunek pierwszego rzędu:
spełniające warunek pierwszego rzędu:
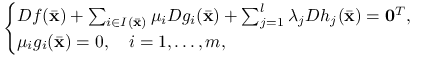 |
(7.3) |
to punkt ![]() jest rozwiązaniem globalnym.
jest rozwiązaniem globalnym.
Dowód
Ustalmy dowolny punkt dopuszczalny ![]() i pomnóżmy obie strony pierwszego równania w warunku (7.3) przez
i pomnóżmy obie strony pierwszego równania w warunku (7.3) przez ![]() :
:
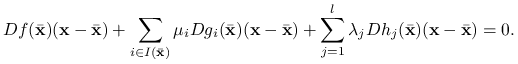 |
Na mocy tw. 7.2 mamy ![]() dla każdego
dla każdego ![]() , bo
, bo ![]() . To samo twierdzenie implikuje, że
. To samo twierdzenie implikuje, że ![]() dla
dla ![]() , ponieważ
, ponieważ ![]() . Korzystając z tych obserwacji wnioskujemy z powyższego równania, że
. Korzystając z tych obserwacji wnioskujemy z powyższego równania, że
Z definicji funkcji pseudowypukłej, ![]() . Punkt
. Punkt ![]() wybraliśmy dowolnie spośród punktów dopuszczalnych, a zatem
wybraliśmy dowolnie spośród punktów dopuszczalnych, a zatem ![]() jest rozwiązaniem globalnym.
jest rozwiązaniem globalnym.
Uwaga 7.3
Jeśli założenia twierdzenia 7.6 są spełnione lokalnie, na pewnym otoczeniu ![]() , to
, to ![]() jest rozwiązaniem lokalnym.
jest rozwiązaniem lokalnym.
Uwaga 7.4
Na mocy twierdzenia 7.4 zamiast zakładać pseudowypukłość funkcji ![]() w punkcie
w punkcie ![]() możemy założyć jej ciągłość na
możemy założyć jej ciągłość na ![]() , quasi-wypukłość oraz warunek
, quasi-wypukłość oraz warunek ![]() . Jest to jedna z form warunku koniecznego zaprezentowana w pracy Arrowa i Enthovena z 1961 roku [1].
. Jest to jedna z form warunku koniecznego zaprezentowana w pracy Arrowa i Enthovena z 1961 roku [1].
Kenneth Joseph Arrow jest amerykańskim ekonomistą. Wspólnie z John'em Hicks'em otrzymał nagrodę Nobla z ekonomii w 1972 roku.
7.4. Zadania
Ćwiczenie 7.1
Udowodnij, że funkcja ![]() jest quasi-liniowa wtw, gdy jest monotoniczna.
jest quasi-liniowa wtw, gdy jest monotoniczna.
Ćwiczenie 7.2
Niech ![]() ,
, ![]() wypukły. Udowodnij następujący fakt: funkcja
wypukły. Udowodnij następujący fakt: funkcja ![]() jest quasi-liniowa wtw, gdy jej obcięcie do każdego odcinka zawartego w
jest quasi-liniowa wtw, gdy jej obcięcie do każdego odcinka zawartego w ![]() jest funkcją monotoniczną.
jest funkcją monotoniczną.
Ćwiczenie 7.3
Wykaż, że jeśli funkcja ![]() ,
, ![]() wypukły, jest quasi-wypukła oraz
wypukły, jest quasi-wypukła oraz ![]() jest niemalejąca, to funkcja
jest niemalejąca, to funkcja ![]() jest quasi-wypukła. Jeśli natomiast funkcja
jest quasi-wypukła. Jeśli natomiast funkcja ![]() jest nierosnąca, to
jest nierosnąca, to ![]() jest quasi-wklęsła.
jest quasi-wklęsła.
Ćwiczenie 7.4
Niech ![]() będzie funkcją jednej zmiennej. Wykaż, że
będzie funkcją jednej zmiennej. Wykaż, że ![]() jest quasi-wypukła wtw, gdy zachodzi jeden z warunków:
jest quasi-wypukła wtw, gdy zachodzi jeden z warunków:
 jest monotoniczna,
jest monotoniczna,istnieje
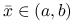 taki że
taki że  jest nierosnąca dla
jest nierosnąca dla 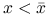 oraz niemalejąca dla
oraz niemalejąca dla 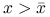 .
.
Ćwiczenie 7.5
Dla jakich wartości parametrów ![]() funkcja
funkcja ![]() jest quasi-wypukła?
jest quasi-wypukła?
Ćwiczenie 7.6
Sprawdź, że funkcja ![]() zadana wzorem
zadana wzorem ![]() jest quasi-wklęsła.
jest quasi-wklęsła.
Ćwiczenie 7.7
Znajdź przykład pokazujący, że suma funkcji quasi-wypukłych nie musi być quasi-wypukła.
Ćwiczenie 7.8
Niech ![]() i
i ![]() . Wykaż, że funkcja wymierna
. Wykaż, że funkcja wymierna
jest quasi-liniowa na swojej dziedzinie ![]()
Ćwiczenie 7.9
Niech ![]() będzie funkcją liniową i
będzie funkcją liniową i ![]() Wykaż, że jeśli
Wykaż, że jeśli ![]() jest wypukła, to funkcja
jest wypukła, to funkcja
![]() dla
dla ![]() jest quasi-wypukła.
jest quasi-wypukła.
Ćwiczenie 7.10
Udowodnij, że jeśli ![]() jest rodziną funkcji quasi-wypukłych,
jest rodziną funkcji quasi-wypukłych, ![]() jest funkcją nieujemną, to
jest funkcją nieujemną, to ![]() jest quasi-wypukła, o ile jest skończona dla każdego
jest quasi-wypukła, o ile jest skończona dla każdego ![]() .
.
Ćwiczenie 7.11
Niech ![]() ,
, ![]() będą zbiorami wypukłymi, zaś
będą zbiorami wypukłymi, zaś ![]() będzie quasi-wypukła. Wykaż, że
będzie quasi-wypukła. Wykaż, że ![]() jest quasi-wypukła.
jest quasi-wypukła.
Ćwiczenie 7.12
Niech ![]() zbiór wypukły,
zbiór wypukły, ![]() . Udowodnij, że jeśli
. Udowodnij, że jeśli ![]() quasi-liniowa, to zbiór
quasi-liniowa, to zbiór ![]() jest wypukły dla dowolnego
jest wypukły dla dowolnego ![]() .
.
Ćwiczenie 7.13
Niech ![]() , ciągła. Udowodnij następującą równoważność:
, ciągła. Udowodnij następującą równoważność: ![]() jest quasi-liniowa wtw, gdy
jest quasi-liniowa wtw, gdy ![]() dla funkcji monotonicznej, ciągłej
dla funkcji monotonicznej, ciągłej ![]() oraz wektora
oraz wektora ![]() .
.
Wykaż, że powyższa równoważność nie musi być prawdziwa, gdy funkcję ![]() rozważamy na wypukłym podzbiorze właściwym
rozważamy na wypukłym podzbiorze właściwym ![]() .
.
Ćwiczenie 7.14
Przeprowadź dowód punktu (II) twierdzenia 7.2.
Dla dowolnych punktów ![]() uporządkowanych tak, że
uporządkowanych tak, że ![]() rozważ funkcję
rozważ funkcję
oraz zbiór
Pokaż, że jeśli zbiór ten jest niepusty, to prowadzi to do sprzeczności z ciągłością funkcji ![]() . Oznacz przez
. Oznacz przez ![]() spójną składową
spójną składową ![]() , tzn. przedział.
, tzn. przedział.
Udowodnij, że
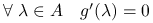 .
.Wykaż, że
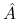 ma niepuste wnętrze.
ma niepuste wnętrze.Wykaż, że funkcja
 jest stała na
jest stała na 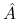 oraz ściśle większa od
oraz ściśle większa od 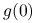 .
.Wykaż, że istnieje przedział otwarty
![I\subset[0,1]](wyklady/op2/mi/mi1282.png) taki że
taki że 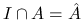 .
.Zauważ sprzeczność z ciągłością funkcji
 , bo
, bo 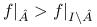 .
.
Ćwiczenie 7.15
Wykaż, że funkcja quasi-wypukła (niekoniecznie ciągła) określona na zbiorze wielościennym zwartym przyjmuje swoje maksimum globalne w jednym z punktów ekstremalnych.
Ćwiczenie 7.16
Rozważmy problem optymalizacyjny (7.1). Niech ![]() będzie punktem dopuszczalnym, w którym spełnione są warunki pierwszego rzędu z mnożnikami Lagrange'a
będzie punktem dopuszczalnym, w którym spełnione są warunki pierwszego rzędu z mnożnikami Lagrange'a ![]() i
i ![]() .
.
Załóżmy, że
 jest pseudowypukła w
jest pseudowypukła w  , zaś funkcja
, zaś funkcja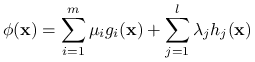
jest quasi-wypukła w
 . Udowodnij, że
. Udowodnij, że  jest rozwiązaniem globalnym.
jest rozwiązaniem globalnym.Przypomnijmy, że
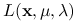 jest funkcją Lagrange'a. Udowodnij, że jeśli
jest funkcją Lagrange'a. Udowodnij, że jeśli 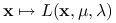 jest pseudowypukła w
jest pseudowypukła w  , to
, to  jest rozwiązaniem globalnym.
jest rozwiązaniem globalnym.Wykaż, że warunki zawarte w powyższych punktach nie są równoważne. Znajdź zależności pomiędzy nimi a założeniami twierdzenia 7.6.
Ćwiczenie 7.17
Niech ![]() będzie rozwiązaniem globalnym problemu optymalizacyjnego (7.1). Załóżmy, że
będzie rozwiązaniem globalnym problemu optymalizacyjnego (7.1). Załóżmy, że ![]() dla pewnego
dla pewnego ![]() . Wykaż, że jeśli ograniczenie
. Wykaż, że jeśli ograniczenie ![]() zostanie usunięte, to
zostanie usunięte, to ![]() może nie być nawet lokalnym rozwiązaniem otrzymanego problemu. Udowodnij natomiast, że jeśli funkcja
może nie być nawet lokalnym rozwiązaniem otrzymanego problemu. Udowodnij natomiast, że jeśli funkcja ![]() jest ciągła w
jest ciągła w ![]() , to po usunięciu tego ograniczenia
, to po usunięciu tego ograniczenia ![]() pozostaje rozwiązaniem lokalnym.
pozostaje rozwiązaniem lokalnym.
Ćwiczenie 7.18
Dla jakich wartości parametru ![]() problem
problem
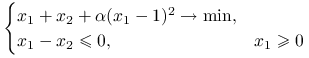 |
ma rozwiązanie? Jak zależy ono od wartości ![]() ?
?
Ćwiczenie 7.19
Rozwiąż zadanie optymalizacyjne:
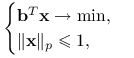 |
gdzie ![]() , zaś
, zaś ![]() i
i ![]() .
.
Ćwiczenie 7.20
Niech ![]() będzie funkcją quasi-wklęsłą o pochodnej
będzie funkcją quasi-wklęsłą o pochodnej ![]() dla każdego
dla każdego ![]() . Ustalmy liczbę
. Ustalmy liczbę ![]() i wektor
i wektor ![]() . Rozważmy problem optymalizacyjny
. Rozważmy problem optymalizacyjny
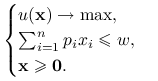 |
Wektor ![]() pełni rolę cen produktów,
pełni rolę cen produktów, ![]() ich ilości,
ich ilości, ![]() jest wielkością budżetu, zaś funkcja
jest wielkością budżetu, zaś funkcja ![]() ocenia satysfakcję z decyzji zakupowej
ocenia satysfakcję z decyzji zakupowej ![]() .
.
Zapisz warunki Kuhn'a-Tucker'a dla powyższego problemu.
Załóżmy, że
 jest rozwiązaniem. Czy będzie wówczas istniał wektor mnożników Lagrange'a, dla którego warunki Kuhn'a-Tucker'a są spełnione w
jest rozwiązaniem. Czy będzie wówczas istniał wektor mnożników Lagrange'a, dla którego warunki Kuhn'a-Tucker'a są spełnione w  ?
?Załóżmy, że warunki Kuhn'a-Tucker'a są spełnione w
 . Czy
. Czy  jest rozwiązaniem problemu optymalizacyjnego?
jest rozwiązaniem problemu optymalizacyjnego?Niech
 będzie rozwiązaniem. Co możesz powiedzieć o związku pomiędzy
będzie rozwiązaniem. Co możesz powiedzieć o związku pomiędzy 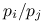 a
a 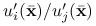 , gdy
, gdy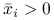 i
i 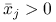 ?
?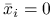 i
i 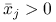 ?
?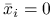 i
i 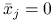 ?
?
Ćwiczenie 7.21
Rozwiąż problem optymalizacyjny
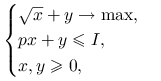 |
gdzie ![]() są parametrami.
są parametrami.
Ćwiczenie 7.22
Niech ![]() będzie macierzą symetryczną
będzie macierzą symetryczną ![]() dodatnio określoną, zaś
dodatnio określoną, zaś ![]() . Rozwiąż problem optymalizacyjny:
. Rozwiąż problem optymalizacyjny:
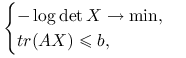 |
w zbiorze macierzy ![]() symetrycznych i dodatnio określonych.
symetrycznych i dodatnio określonych.