Zagadnienia

8.1 Warunek konieczny pierwszego rzędu
8.2 Warunki regularności

8. Warunek konieczny dla ograniczeń mieszanych

W tym rozdziale wyprowadzimy warunek konieczny pierwszego rzędu dla problemu optymalizacyjnego w następującej formie:

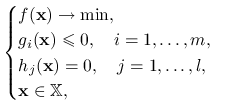$\begin{cases}f(\mathbf{x})\to\min,&\\ g_{i}(\mathbf{x})\le 0,\quad i=1,\ldots,m,&\\ h_{j}(\mathbf{x})=0,\quad j=1,\ldots,l,&\\ \mathbf{x}\in\mathbb{X},\end{cases}$

(8.1)

gdzie $\mathbb{X}\subset\mathbb{R}^{n}$ jest zbiorem otwartym i $f,g_{1},\ldots,g_{m},h_{1},\ldots,h_{l}:\mathbb{X}\to\mathbb{R}$ . Zbiór punktów dopuszczalnych zadany jest następująco:

$W=\big\{\mathbf{x}\in\mathbb{X}:g_{1}(\mathbf{x})\le 0,\ldots,g_{m}(\mathbf{x})\le 0,\ h_{1}(\mathbf{x})=0,\ldots,h_{l}(\mathbf{x})=0\big\}.$

(8.2)

Przypomnijmy, że funkcje $g_{i}$ nazywane są ograniczeniami nierównościowymi, funkcje $h_{j}$ są ograniczeniami równościowymi, zaś cały problem (8.1) nazywa się zadaniem optymalizacyjnym z ograniczeniami mieszanymi.

Przykład 8.1

Rozważmy następujący problem optymalizacyjny:

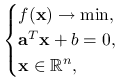$\begin{cases}f(\mathbf{x})\to\min,&\\ \mathbf{a}^{T}\mathbf{x}+b=0,&\\ \mathbf{x}\in\mathbb{R}^{n},&\end{cases}$

dla pewnego $\mathbf{a}\in\mathbb{R}^{n}$ i $b\in\mathbb{R}$ . Ograniczenie równościowe możemy zamienić na dwa ograniczenia nierównościowe:

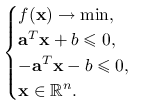$\begin{cases}f(\mathbf{x})\to\min,&\\ \mathbf{a}^{T}\mathbf{x}+b\le 0,&\\ -\mathbf{a}^{T}\mathbf{x}-b\le 0,&\\ \mathbf{x}\in\mathbb{R}^{n}.&\end{cases}$

Ograniczenia są afiniczne, czyli w każdym punkcie spełniony jest warunek afiniczności. Jeśli ${\bar{\mathbf{x}}}$ jest rozwiązaniem lokalnym, to istnieje wektor mnożników Lagrange'a $\mu=[\mu _{1},\mu _{2}]^{T}$ i spełnione są warunki Kuhna-Tuckera (5.5):

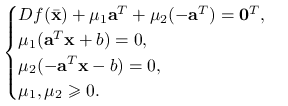$\begin{cases}Df({\bar{\mathbf{x}}})+\mu _{1}\mathbf{a}^{T}+\mu _{2}(-\mathbf{a}^{T})=\mathbf{0}^{T},&\\ \mu _{1}(\mathbf{a}^{T}\mathbf{x}+b)=0,&\\ \mu _{2}(-\mathbf{a}^{T}\mathbf{x}-b)=0,&\\ \mu _{1},\mu _{2}\ge 0.&\end{cases}$

Punkt ${\bar{\mathbf{x}}}$ jest dopuszczalny (jako że jest rozwiązaniem), czyli spełnia ograniczenia: $\mathbf{a}^{T}\mathbf{x}+b=0$ . Stąd trywialnie spełnione są druga i trzecia równość. Możemy zatem powyższe warunki równoważnie zapisać jako:

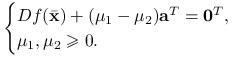$\begin{cases}Df({\bar{\mathbf{x}}})+(\mu _{1}-\mu _{2})\mathbf{a}^{T}=\mathbf{0}^{T},&\\ \mu _{1},\mu _{2}\ge 0.&\end{cases}$

Oznaczmy $\lambda=\mu _{1}-\mu _{2}$ . Warunki nieujemności $\mu _{1},\mu _{2}$ implikują, że $\lambda\in\mathbb{R}$ . Dostajemy więc finalnie:

$Df({\bar{\mathbf{x}}})+\lambda\mathbf{a}^{T}=\mathbf{0}^{T},\qquad\lambda\in\mathbb{R}.$

Jest to warunek Kuhna-Tuckera dla ograniczeń równościowych.

Powyższy przykład sugerowałby, że teoria dla problemów z ograniczeniami nierównościowymi, zbudowana w poprzednich rozdziałach, pozwala poradzić sobie z ograniczeniami równościowymi. Niestety nie jest to prawda. Ograniczenia afiniczne są szczególnym przypadkiem. Jeśli któreś z ograniczeń równościowych nie jest afiniczne i rozbijemy je na dwie nierówności, jak powyżej, to w żadnym punkcie zbioru $W$ nie jest spełniony ani warunek liniowej zależności ograniczeń ani warunek Slatera.

8.1. Warunek konieczny pierwszego rzędu

Teoria wprowadzana w tym podrozdziale jest prostym rozszerzeniem tego, co już zrobiliśmy dla problemu optymalizacyjnego z ograniczeniami nierównościowymi. Rozpoczniemy od rozszerzenia $T_{{lin}}$ :

Definicja 8.1

Niech ${\bar{\mathbf{x}}}\in W$ , $g_{i}$ różniczkowalne w ${\bar{\mathbf{x}}}$ dla ograniczeń aktywnych $i\in I({\bar{\mathbf{x}}})$ oraz $h_{j}$ są różniczkowalne w ${\bar{\mathbf{x}}}$ dla $j=1,\ldots,l$ . Stożkiem kierunków stycznych dla ograniczeń zlinearyzowanych nazywamy zbiór

$T_{{lin}}({\bar{\mathbf{x}}})=\big\{\mathbf{d}\in\mathbb{R}^{n}:\ \forall i\in I({\bar{\mathbf{x}}})\quad Dg_{i}({\bar{\mathbf{x}}})\mathbf{d}\le 0,\quad\forall j=1,\ldots,l\quad Dh_{j}({\bar{\mathbf{x}}})\mathbf{d}=0\big\}.$

Podobnie jak poprzednio zauważmy, że stożek kierunków stycznych dla ograniczeń zlinearyzowanych jest zbiorem wielościennym, a zatem wypukłym i domkniętym. Jeśli jest choć jedno ograniczenie równościowe, to ma on puste wnętrze.

Warunek konieczny istnienia rozwiązania lokalnego problemu z ograniczeniami mieszanymi jest sformułowany poniżej. Identycznie jak w twierdzeniu 5.2 zakładamy równość stożka kierunków stycznych dla ograniczeń oryginalnych i zlinearyzowanych. Później uogólnimy warunki regularności, które będą taką równość pociągały.

Twierdzenie 8.1 (Twierdzenia Kuhna-Tuckera)

Niech ${\bar{\mathbf{x}}}$ będzie rozwiązaniem lokalnym (8.1). Jeśli funkcje $f$ , $g_{i}$ , $i\in I({\bar{\mathbf{x}}})$ , oraz $h_{j}$ , $j=1,\ldots,l$ , są różniczkowalne w ${\bar{\mathbf{x}}}$ oraz $T({\bar{\mathbf{x}}})=T_{{lin}}({\bar{\mathbf{x}}})$ , to istnieją $\mu\in[0,\infty)^{m}$ oraz $\lambda\in\mathbb{R}^{l}$ takie że

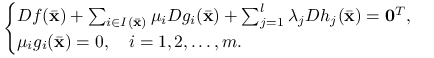$\begin{cases}Df({\bar{\mathbf{x}}})+\sum _{{i\in I({\bar{\mathbf{x}}})}}\mu _{i}Dg_{i}({\bar{\mathbf{x}}})+\sum _{{j=1}}^{l}\lambda _{j}Dh_{j}({\bar{\mathbf{x}}})=\mathbf{0}^{T},&\\ \mu _{i}g_{i}({\bar{\mathbf{x}}})=0,\quad i=1,2,\ldots,m.&\end{cases}$

(8.3)

Dowód

Na mocy twierdzenia 5.1 mamy $D({\bar{\mathbf{x}}})\cap T({\bar{\mathbf{x}}})=\emptyset$ . Dalej, korzystając z założenia, dostajemy $D({\bar{\mathbf{x}}})\cap T_{{lin}}({\bar{\mathbf{x}}})=\emptyset$ , co innymi słowy oznacza, że nie istnieje rozwiązanie $\mathbf{z}\in\mathbb{R}^{n}$ układu

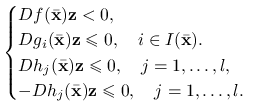$\begin{cases}Df({\bar{\mathbf{x}}})\mathbf{z}<0,&\\ Dg_{i}({\bar{\mathbf{x}}})\mathbf{z}\le 0,\quad i\in I({\bar{\mathbf{x}}}).&\\ Dh_{j}({\bar{\mathbf{x}}})\mathbf{z}\le 0,\quad j=1,\ldots,l,&\\ -Dh_{j}({\bar{\mathbf{x}}})\mathbf{z}\le 0,\quad j=1,\ldots,l.&\end{cases}$

(8.4)

Stosujemy lemat Farkasa, lemat 5.3, z $\mathbf{d}=-Df({\bar{\mathbf{x}}})$ i macierzą $A$ następującej postaci:

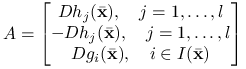$A=\begin{bmatrix}Dh_{j}({\bar{\mathbf{x}}}),\quad j=1,\ldots,l\\ -Dh_{j}({\bar{\mathbf{x}}}),\quad j=1,\ldots,l\\ Dg_{i}({\bar{\mathbf{x}}}),\quad i\in I({\bar{\mathbf{x}}})\end{bmatrix}$

Istnieje zatem $\mathbf{y}\in[0,\infty)^{{|I({\bar{\mathbf{x}}})|+2l}}$ takie że $\mathbf{y}^{T}A=-Df({\bar{\mathbf{x}}})$ lub inaczej

$Df({\bar{\mathbf{x}}})+\mathbf{y}^{T}A=\mathbf{0}^{T}.$

(8.5)

Zdefiniujmy $\lambda _{j}=y_{j}-y_{{l+j}}$ , $j=1,\ldots,l$ . Przypiszmy współrzędnym $\mu$ odpowiadającym ograniczeniom aktywnym, $i\in I({\bar{\mathbf{x}}})$ , ostatnie $|I({\bar{\mathbf{x}}})|$ wartości wektora $y$ . Na pozostałych współrzędnych połóżmy zera. Wówczas równość (8.5) jest równoważna następującej

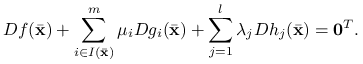$Df({\bar{\mathbf{x}}})+\sum _{{i\in I({\bar{\mathbf{x}}})}}^{m}\mu _{i}Dg_{i}({\bar{\mathbf{x}}})+\sum _{{j=1}}^{l}\lambda _{j}Dh_{j}({\bar{\mathbf{x}}})=\mathbf{0}^{T}.$

Z definicji $\mu _{i}$ oczywiste jest, że $\mu _{i}g_{i}({\bar{\mathbf{x}}})=0$ .

∎

8.2. Warunki regularności

Sformułujemy teraz trzy warunki dostateczne równości $T({\bar{\mathbf{x}}})=T_{{lin}}({\bar{\mathbf{x}}})$ , zwane warunkami regularności.

Definicja 8.2

W punkcie ${\bar{\mathbf{x}}}\in W$ spełniony jest:

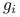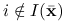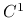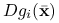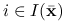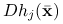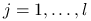warunek liniowej niezależności, jeśli funkcje $g_{i}$ , $i\notin I({\bar{\mathbf{x}}})$ , są ciągłe w ${\bar{\mathbf{x}}}$ , pozostałe ograniczenia nierównościowe i wszystkie równościowe są klasy $C^{1}$ na otoczeniu ${\bar{\mathbf{x}}}$ oraz wektory $Dg_{i}({\bar{\mathbf{x}}})$ dla $i\in I({\bar{\mathbf{x}}})$ i $Dh_{j}({\bar{\mathbf{x}}})$ dla $j=1,\ldots,l$ są liniowo niezależne,
warunek afiniczności, jeśli funkcje 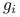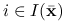$g_{i}$ , $i\in I({\bar{\mathbf{x}}})$ , oraz 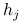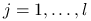$h_{j}$ , $j=1,\ldots,l$ , są afiniczne,
warunek Slatera, jeśli
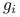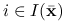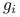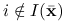- funkcje $g_{i}$ , $i\in I({\bar{\mathbf{x}}})$ są pseudowypukłe w ${\bar{\mathbf{x}}}$ , funkcje $g_{i}$ , $i\notin I({\bar{\mathbf{x}}})$ , są ciągłe w ${\bar{\mathbf{x}}}$ ,
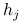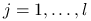- funkcje $h_{j}$ , $j=1,\ldots,l$ , są afiniczne,
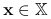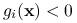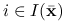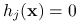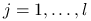- istnieje $\mathbf{x}\in\mathbb{X}$ , dla którego $g_{i}(\mathbf{x})<0$ dla $i\in I({\bar{\mathbf{x}}})$ oraz $h_{j}(\mathbf{x})=0$ dla $j=1,\ldots,l$ .

Zaczniemy od najprostszego przypadku.

Twierdzenie 8.2

Jeśli w punkcie ${\bar{\mathbf{x}}}\in W$ spełniony jest warunek afiniczności, to zachodzi równość $T({\bar{\mathbf{x}}})=T_{{lin}}({\bar{\mathbf{x}}})$ .

Dowód

Postępując jak w przykładzie 8.1 zamieniamy ograniczenia afiniczne równościowe na ograniczenia afiniczne nierównościowe. Teza wynika z twierdzenia 6.1.

∎

Twierdzenie 8.3

Jeśli w punkcie ${\bar{\mathbf{x}}}\in W$ spełniony jest warunek Slatera, to zachodzi równość $T({\bar{\mathbf{x}}})=T_{{lin}}({\bar{\mathbf{x}}})$ .

Dowód

Zapiszmy najpierw funkcje $h_{j}$ dla $j=1,\ldots,l$ :

$h_{j}(\mathbf{y})=\mathbf{a}_{j}^{T}\mathbf{y}+b_{j},\qquad\mathbf{a}_{j}\in\mathbb{R}^{n},\quad b_{j}\in\mathbb{R}.$

Wprowadźmy uogólnienie zbioru $T_{{int}}({\bar{\mathbf{x}}})$ do przypadku ograniczeń mieszanych:

$T_{{int}}({\bar{\mathbf{x}}})=\big\{\mathbf{d}\in\mathbb{R}^{n}:\ \forall i\in I({\bar{\mathbf{x}}})\quad Dg_{i}({\bar{\mathbf{x}}})\mathbf{d}<0,\quad\forall j=1,\ldots,l\quad Dh_{j}({\bar{\mathbf{x}}})\mathbf{d}=0\big\}.$

(1) $T_{{int}}({\bar{\mathbf{x}}})\ne\emptyset.$ Weźmy punkt $\mathbf{x}$ z warunku Slatera. Na mocy pseudowypukłości, patrz uwaga 4.3, mamy

$Dg_{i}({\bar{\mathbf{x}}})(\mathbf{x}-{\bar{\mathbf{x}}})<0,\qquad\forall\ i\in I({\bar{\mathbf{x}}}).$

Dla każdego $j$ mamy także

$\mathbf{a}_{j}^{T}(\mathbf{x}-{\bar{\mathbf{x}}})=\mathbf{a}_{j}^{T}\mathbf{x}+b_{j}-\mathbf{a}_{j}^{T}{\bar{\mathbf{x}}}-b_{j}=h_{j}(\mathbf{x})-h_{j}({\bar{\mathbf{x}}})=0.$

Wnioskujemy więc, że wektor $(\mathbf{x}-{\bar{\mathbf{x}}})\in T_{{int}}({\bar{\mathbf{x}}})$ .

(2) $T_{{int}}({\bar{\mathbf{x}}})\subset T({\bar{\mathbf{x}}})$ . W tym celu weźmy dowolny $\mathbf{d}\in T_{{int}}({\bar{\mathbf{x}}})$ . Wystarczy pokazać, że pewien odcinek o końcu ${\bar{\mathbf{x}}}$ i kierunku $\mathbf{d}$ zawiera się w całości w zbiorze $W$ . Rozważmy w tym celu funkcję $\mathbf{y}(\lambda)=\mathbf{x}+\lambda\mathbf{d}.$ Na mocy ciągłości funkcji opisujących ograniczenia nieaktywne istnieje $\varepsilon>0$ taki że $g_{i}\big(\mathbf{y}(\lambda)\big)\le 0$ dla $\lambda\in[0,\varepsilon]$ oraz $i\notin I({\bar{\mathbf{x}}})$ . Z faktu, że $\mathbf{d}\in T_{{int}}({\bar{\mathbf{x}}})$ dostajemy również, że $h_{j}\big(\mathbf{y}(\lambda)\big)=0$ dla $j=1,\ldots,l$ i dowolnego $\lambda$ . Pozostaje tylko zająć się ograniczeniami aktywnymi. Z faktu, że $g_{i}$ są różniczkowalne w ${\bar{\mathbf{x}}}$ dla $i\in I({\bar{\mathbf{x}}})$ mamy

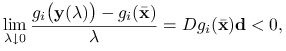$\lim _{{\lambda\downarrow 0}}\frac{g_{i}\big(\mathbf{y}(\lambda)\big)-g_{i}({\bar{\mathbf{x}}})}{\lambda}=Dg_{i}({\bar{\mathbf{x}}})\mathbf{d}<0,$

gdzie ostatnia nierówność wynika z tego, że $\mathbf{d}\in T_{{int}}({\bar{\mathbf{x}}})$ . A zatem $g_{i}\big(\mathbf{y}(\lambda)\big)-g_{i}({\bar{\mathbf{x}}})<0$ dla dostatecznie małych $\lambda$ .

(3) $\mathop{\rm cl}T_{{int}}({\bar{\mathbf{x}}})=T_{{lin}}({\bar{\mathbf{x}}})$ . Zbiory $T_{{int}}({\bar{\mathbf{x}}})$ i $T_{{lin}}({\bar{\mathbf{x}}})$ leżą na hiperpłaszczyźnie $H$ wyznaczonej przez afiniczne ograniczenia liniowe. Możemy zatem znaleźć przekształcenie liniowe $P$ o pełnym rzędzie przekształcające tą hiperpłaszczyznę w przestrzeń $\mathbb{R}^{{n^{{\prime}}}}$ , gdzie $n^{{\prime}}$ jest wymiarem rzeczonej hiperpłaszczyzny (jeśli funkcje $h_{j}$ są parami różne, to $n^{{\prime}}=n-l$ ). Przekształcenie to jest wzajemnie jednoznaczne rozpatrywane jako funkcja określona na $H$ . A zatem topologie w $\mathbb{R}^{{n^{{\prime}}}}$ i na $H$ są identyczne. Wystarczy więc udowodnić tezę tego podpunktu na obrazach $T^{{\prime}}_{{int}}({\bar{\mathbf{x}}})$ i $T^{{\prime}}_{{lin}}({\bar{\mathbf{x}}})$ zbiorów $T_{{int}}({\bar{\mathbf{x}}})$ i $T_{{lin}}({\bar{\mathbf{x}}})$ . Zauważmy, że zbiór $T^{{\prime}}_{{int}}({\bar{\mathbf{x}}})$ jest otwarty. Wykazaliśmy, że jest niepusty. Jest również wnętrzem zbioru $T^{{\prime}}_{{lin}}({\bar{\mathbf{x}}})$ . Na mocy lematu 6.1 mamy $\mathop{\rm cl}T^{{\prime}}_{{int}}({\bar{\mathbf{x}}})=T^{{\prime}}_{{lin}}({\bar{\mathbf{x}}})$ .

(4) $T({\bar{\mathbf{x}}})\subset T_{{lin}}({\bar{\mathbf{x}}})$ . Identycznie jak dowód lematu 5.2.

Pozostaje już tylko przypomnieć, że $T({\bar{\mathbf{x}}})$ jest zbiorem domkniętym. A zatem

$\mathop{\rm cl}T_{{int}}({\bar{\mathbf{x}}})\subset T({\bar{\mathbf{x}}})\subset T_{{lin}}=\mathop{\rm cl}T_{{int}}({\bar{\mathbf{x}}}).$

∎

Zanim przejdziemy do rozważań nad trzecim warunkiem regularności, warunkiem liniowej niezależności, przypomnijmy twierdzenie o funkcji uwikłanej, by, korzystając z niego, podać opis stożka kierunków stycznych do powierzchni zadanej przez ograniczenia równościowe.

Twierdzenie 8.4 (Twierdzenie o funkcji uwikłanej)

Niech $f:\mathbb{X}\to\mathbb{R}^{n}$ , gdzie $\mathbb{X}\subset\mathbb{R}^{{n+m}}$ otwarty, będzie odwzorowaniem klasy $C^{k}$ . Załóżmy, że $f(\mathbf{a},\mathbf{b})=\mathbf{0}$ , gdzie $(\mathbf{a},\mathbf{b})\in\mathbb{X}$ . Przyjmujemy tutaj notację, że $\mathbf{a}\in\mathbb{R}^{n}$ , zaś $\mathbf{b}\in\mathbb{R}^{m}$ . Oznaczmy przez $A_{x}$ macierz pochodnych cząstkowych, w punkcie $(\mathbf{a},\mathbf{b})$ , względem pierwszych $n$ zmiennych: $A_{x}\in\mathbb{R}^{{n\times n}}$ zadana jest wzorem $(A_{x})_{{ij}}=\frac{\partial f_{i}}{\partial u_{j}}(\mathbf{a},\mathbf{b}).$

Jeśli macierz $A_{x}$ jest odwracalna, to istnieje zbiór otwarty $W\subset\mathbb{R}^{m}$ zawierający $\mathbf{b}$ oraz funkcja $g:W\to\mathbb{R}^{{n}}$ klasy $C^{k}$ , taka że $\big(g(\mathbf{y}),\mathbf{y}\big)\in\mathbb{X}$ dla $\mathbf{y}\in W$ , $g(\mathbf{b})=\mathbf{a}$ oraz $f\big(g(\mathbf{y}),\mathbf{y}\big)=\mathbf{0}$ dla $\mathbf{y}\in W$ . Ponadto, $Dg(\mathbf{b})=-(A_{x})^{{-1}}A_{y}$ , gdzie $A_{y}$ jest pochodną $f$ w punkcie $(\mathbf{a},\mathbf{b})$ względem ostatnich $m$ zmiennych: $A_{y}\in\mathbb{R}^{{n\times m}}$ zadana jest wzorem $(A_{y})_{{ij}}=\frac{\partial f_{i}}{\partial u_{{n+j}}}(\mathbf{a},\mathbf{b}).$

Rozważmy powierzchnię opisaną przez układ $m^{*}$ równań:

$S=\big\{\mathbf{x}\in\mathbb{X}:\ c_{i}(\mathbf{x})=0,\quad i=1,\ldots,m^{*}\},$

gdzie $\mathbb{X}\subset\mathbb{R}^{n}$ otwarty. Przez $T^{S}({\bar{\mathbf{x}}})$ oznaczmy stożek kierunków stycznych do $S$ punkcie ${\bar{\mathbf{x}}}\in S$ .

Twierdzenie 8.5

Załóżmy, że funkcje $c_{i}$ , $i=1,\ldots,m^{*},$ są klasy $C^{k}$ , $k\ge 1$ , na otoczeniu ${\bar{\mathbf{x}}}$ oraz gradienty $Dc_{i}({\bar{\mathbf{x}}})$ , $i=1,\ldots,m^{*}$ , są liniowo niezależne. Wówczas

$T^{S}({\bar{\mathbf{x}}})=T^{S}_{{lin}}({\bar{\mathbf{x}}}):=\big\{\mathbf{d}\in\mathbb{R}^{n}:\ Dc_{i}({\bar{\mathbf{x}}})\mathbf{d}=0,\quad i=1,\ldots,m^{*}\big\}.$

Ponadto, dla każdego $\mathbf{d}\in T^{S}({\bar{\mathbf{x}}})$ istnieje $\varepsilon>0$ i krzywa $\mathbf{y}:(-\varepsilon,\varepsilon)\to S$ klasy $C^{k}$ o tej własności, że $y(0)={\bar{\mathbf{x}}}$ oraz $\mathbf{y}^{{\prime}}(0)=\mathbf{d}$ .

Dowód

Pokażemy najpierw, że $T^{S}({\bar{\mathbf{x}}})\subset T^{S}_{{lin}}({\bar{\mathbf{x}}})$ . Niech $\mathbf{d}\in T^{S}({\bar{\mathbf{x}}})$ . Wówczas $\mathbf{d}=\lim _{{k\to\infty}}\lambda _{k}(\mathbf{x}_{k}-{\bar{\mathbf{x}}})$ dla $(\mathbf{x}_{k})\subset S$ , $\mathbf{x}_{k}\ne\mathbf{x}$ . Z definicji pochodnej dostajemy dla każdego $i=1,\ldots,m^{*}$ :

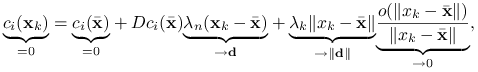$\underset{=0}{\underbrace{c_{i}(\mathbf{x}_{k})}}=\underset{=0}{\underbrace{c_{i}({\bar{\mathbf{x}}})}}+Dc_{i}({\bar{\mathbf{x}}})\underset{\to\mathbf{d}}{\underbrace{\lambda _{n}(\mathbf{x}_{k}-{\bar{\mathbf{x}}})}}+\underset{\to\|\mathbf{d}\|}{\underbrace{\lambda _{k}\| x_{k}-{\bar{\mathbf{x}}}\|}}\underset{\to 0}{\underbrace{\frac{o(\| x_{k}-{\bar{\mathbf{x}}}\|)}{\| x_{k}-{\bar{\mathbf{x}}}\|}}},$

czyli $Dc_{i}({\bar{\mathbf{x}}})\mathbf{d}=0$ . Stąd wynika, że $\mathbf{d}\in T^{S}_{{lin}}({\bar{\mathbf{x}}})$ .

Pozostało jeszcze zawieranie w drugą stronę. Dowód tej części będzie zdecydowanie trudniejszy. Ustalmy $\mathbf{d}\in T^{S}_{{lin}}({\bar{\mathbf{x}}})$ . Skonstruujemy krzywą przechodzącą przez ${\bar{\mathbf{x}}}$ i zawartą w $S$ , której pochodna w punkcie ${\bar{\mathbf{x}}}$ jest równa $\mathbf{d}$ . Oznaczmy $c(\mathbf{x})=\big(c_{1}(\mathbf{x}),\ldots,c_{{m^{*}}}(\mathbf{x})\big)$ i zdefiniujmy funkcję $\Phi:\mathbb{R}^{{m^{*}}}\times\mathbb{R}\to\mathbb{R}^{{m^{*}}}$ wzorem

$\Phi(u,t)=c\big({\bar{\mathbf{x}}}+t\mathbf{d}+(Dc({\bar{\mathbf{x}}}))^{T}u\big).$

Zauważmy, że $\Phi(\mathbf{0},0)=\mathbf{0}$ . Oznaczmy przez $D_{u}\Phi$ macierz pochodnych cząstkowych względem zmiennych wektora $u$ : $D_{u}\Phi=(\frac{\partial\Phi _{i}}{\partial u_{j}})_{{i,j=1}}^{{m^{*}}}.$ W $(\mathbf{0},0)$ mamy $D_{u}\Phi(\mathbf{0},0)=Dc({\bar{\mathbf{x}}})\big(Dc({\bar{\mathbf{x}}})\big)^{T}$ . Przypomnijmy, że zgodnie z założeniem macierz $Dc({\bar{\mathbf{x}}})$ ma maksymalny rząd (równy $m^{*}$ ), czyli $D_{u}\Phi(\mathbf{0},0)$ jest odwracalna. Na mocy twierdzenia o funkcji uwikłanej istnieje zatem $\varepsilon>0$ oraz funkcja $u:(-\varepsilon,\varepsilon)\to\mathbb{R}^{{m^{*}}}$ klasy $C^{k}$ , taka że $\Phi\big(u(t),t\big)=\mathbf{0}$ . Połóżmy

$y(t)={\bar{\mathbf{x}}}+t\mathbf{d}+(Dc({\bar{\mathbf{x}}}))^{T}u(t).$

Krzywa ta, zgodnie z konstrukcją, leży na powierzchni $S$ , tzn. $c(y(t))=\mathbf{0}$ dla $t\in(-\varepsilon,\varepsilon)$ oraz $y(0)={\bar{\mathbf{x}}}$ . Różniczkując złożenie $c(y(t))$ dostajemy

$\frac{d}{dt}c\big(y(t)\big)=Dc\big(y(t)\big)\big(\mathbf{d}+(Dc({\bar{\mathbf{x}}}))^{T}u^{{\prime}}(t)\big).$

czyli w $t=0$ mamy

$\frac{d}{dt}c\big(y(t)\big)\big|_{{t=0}}=Dc({\bar{\mathbf{x}}})\big(\mathbf{d}+(Dc({\bar{\mathbf{x}}}))^{T}u^{{\prime}}(0)\big).$

Z drugiej strony wiemy, że $c(y(t))=\mathbf{0}$ , czyli powyższa pochodna jest równa zero: $Dc({\bar{\mathbf{x}}})\big(\mathbf{d}+(Dc({\bar{\mathbf{x}}}))^{T}u^{{\prime}}(0)\big)=\mathbf{0}$ . Przypomnijmy, że $\mathbf{d}\in T^{S}_{{lin}}({\bar{\mathbf{x}}})$ , co w naszym zapisie oznacza $Dc({\bar{\mathbf{x}}})\mathbf{d}=\mathbf{0}$ . Wynika stąd, że $Dc({\bar{\mathbf{x}}})(Dc({\bar{\mathbf{x}}}))^{T}u^{{\prime}}(0)=\mathbf{0}$ . Korzystając z faktu, że $Dc({\bar{\mathbf{x}}})$ ma rząd $m^{*}$ dostajemy $u^{{\prime}}(0)=\mathbf{0}$ . Jesteśmy już teraz gotowi, aby dokończyć dowód. Różniczkując funkcję $y$ dostajemy

$y^{{\prime}}(t)=\mathbf{d}+(Dc({\bar{\mathbf{x}}}))^{T}u^{{\prime}}(t),$

co w $t=0$ daje $y^{{\prime}}(0)=\mathbf{d}$ . Możemy stąd już łatwo wywnioskować, że $\mathbf{d}\in T^{S}({\bar{\mathbf{x}}})$ .

∎

Uwaga 8.1

Powyższe twierdzenie dowodzi powszechnie znanego faktu dotyczącego przestrzeni stycznej do rozmaitości. Otóż, z założeń wynika, że $S$ jest lokalnie wokół punktu ${\bar{\mathbf{x}}}$ rozmaitością różniczkową klasy $C^{k}$ . Przestrzeń styczna do rozmaitości w punkcie ${\bar{\mathbf{x}}}$ definiowana jest jako zbiór wektorów, które są pochodnymi (w punkcie ${\bar{\mathbf{x}}}$ ) krzywych leżących na tej rozmaitości i przechodzących przez ${\bar{\mathbf{x}}}$ (jest to równoważne definicji $T({\bar{\mathbf{x}}})$ ). Równość $T_{{lin}}({\bar{\mathbf{x}}})=T({\bar{\mathbf{x}}})$ oznacza, że przestrzeń styczna jest jądrem przekształcenia liniowego $Dc({\bar{\mathbf{x}}})$ .

Z powyższego twierdzenia będziemy wielokrotnie korzystać w następnych rozdziałach. Będzie ono głównym narzędziem przy dowodzeniu warunku koniecznego drugiego rzędu. W tym rozdziale pozwoli łatwo wykazać równość $T({\bar{\mathbf{x}}})=T_{{lin}}({\bar{\mathbf{x}}})$ przy założeniu warunku liniowej niezależności.

Twierdzenie 8.6

Jeśli w punkcie ${\bar{\mathbf{x}}}\in W$ spełniony jest warunek liniowej niezależności, to zachodzi równość $T({\bar{\mathbf{x}}})=T_{{lin}}({\bar{\mathbf{x}}})$ .

Dowód

Ustalmy $\mathbf{d}\in T_{{lin}}({\bar{\mathbf{x}}})$ . Niech $\hat{I}({\bar{\mathbf{x}}})=\{ i\in I({\bar{\mathbf{x}}}):\ Dg_{i}({\bar{\mathbf{x}}})\mathbf{d}=0\}$ . Na mocy twierdzenia 8.5 istnieje krzywa $y:(-\varepsilon,\varepsilon)\to\mathbb{R}^{n}$ , taka że $y(0)={\bar{\mathbf{x}}}$ , $y^{{\prime}}(0)=\mathbf{d}$ oraz $g_{i}\big(y(t)\big)=0$ , $i\in\hat{I}({\bar{\mathbf{x}}})$ , i $h_{j}\big(y(t)\big)=0$ , $j=1,\ldots,l.$ Ustalmy $i\in I({\bar{\mathbf{x}}})\setminus\hat{I}({\bar{\mathbf{x}}})$ . Połóżmy $\hat{g}_{i}(t)=g_{i}(y(t))$ , $t\in(-\varepsilon,\varepsilon)$ . Wówczas $\hat{g}^{{\prime}}_{i}(0)=Dg_{i}({\bar{\mathbf{x}}})\mathbf{d}<0$ , czyli istnieje $\varepsilon _{i}>0$ , takie że $\hat{g}_{i}(t)<0$ dla $t\in[0,\varepsilon _{i})$ . Z ciągłości, $g_{i}(y(t))<0$ na pewnym otoczeniu $0$ dla $i\notin I({\bar{\mathbf{x}}})$ . Podsumowując, istnieje $\bar{\varepsilon}>0$ , takie że $y(t)\in W$ dla $t\in[0,\bar{\varepsilon})$ . Stąd trywialnie $\mathbf{d}\in T({\bar{\mathbf{x}}})$ .