Zagadnienia
1. Wiadomości wstępne
1.1. Problem optymalizacji
Niech ![]() będzie niepustym zbiorem, zaś
będzie niepustym zbiorem, zaś ![]() dowolną funkcją. Będziemy rozważać problem minimalizacji funkcji
dowolną funkcją. Będziemy rozważać problem minimalizacji funkcji ![]() na zbiorze
na zbiorze ![]() , przyjmując różne postaci
, przyjmując różne postaci ![]() , w tym:
, w tym:
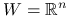 (problem optymalizacji bez ograniczeń),
(problem optymalizacji bez ograniczeń),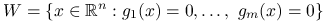 , gdzie
, gdzie 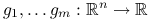 pewne funkcje (problem optymalizacji z ograniczeniami równościowymi),
pewne funkcje (problem optymalizacji z ograniczeniami równościowymi),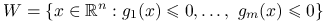 , gdzie
, gdzie 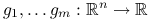 pewne funkcje (problem optymalizacji z ograniczeniami nierównościowymi).
pewne funkcje (problem optymalizacji z ograniczeniami nierównościowymi).
Zbiór ![]() nosi nazwę zbioru punktów dopuszczalnych.
nosi nazwę zbioru punktów dopuszczalnych.
Definicja 1.1
Punkt ![]() nazywamy minimum globalnym
funkcji
nazywamy minimum globalnym
funkcji ![]() na zbiorze
na zbiorze ![]() jeśli
jeśli
Definicja 1.2
Punkt ![]() nazywamy minimum lokalnym
funkcji
nazywamy minimum lokalnym
funkcji ![]() jeśli istnieje
jeśli istnieje ![]() takie, że dla kuli
takie, że dla kuli
![]() o środku w
o środku w ![]() i promieniu
i promieniu ![]() zachodzi
zachodzi
Oczywiście, jeśli ![]() jest minimum globalnym to jest minimum
lokalnym. Minimum nazywamy ścisłym, jeśli w
powyższych definicjach zachodzi
jest minimum globalnym to jest minimum
lokalnym. Minimum nazywamy ścisłym, jeśli w
powyższych definicjach zachodzi ![]() , dla
, dla ![]() .
Analogicznie definiujemy globalne i lokalne maksimum. Punkt
.
Analogicznie definiujemy globalne i lokalne maksimum. Punkt ![]() nazywamy ekstremum (lokalnym, globalnym) jeśli jest on
maksimum lub minimum (lokalnym, globalnym).
nazywamy ekstremum (lokalnym, globalnym) jeśli jest on
maksimum lub minimum (lokalnym, globalnym).
Minimum (globalne, lokalne) nie musi istnieć, tzn. może się
okazać, że nie istnieje ![]() spełniające warunek z
definicji 1.1 lub 1.2. W szczególności minimum
globalne
spełniające warunek z
definicji 1.1 lub 1.2. W szczególności minimum
globalne ![]() na zbiorze
na zbiorze ![]() nie istnieje gdy:
nie istnieje gdy:
(a)
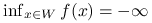 , lub
, lub(b)
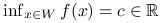 , ale
, ale 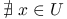 takie, że
takie, że
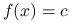 .
.
Przykład 1.1
Niech ![]() . Dla tej funkcji
. Dla tej funkcji
![]() , zatem minimum globalne nie istnieje.
Jeżeli natomiast ograniczymy się do przedziału
, zatem minimum globalne nie istnieje.
Jeżeli natomiast ograniczymy się do przedziału ![]() ,
to minimum globalne będzie istnieć. Funkcja ta osiąga
minimum lokalne w nieskończonej ilości punktów, dla
,
to minimum globalne będzie istnieć. Funkcja ta osiąga
minimum lokalne w nieskończonej ilości punktów, dla ![]() .
Jeżeli za
.
Jeżeli za ![]() przyjmiemy odcinek otwarty, to minimum globalne
istnieje lub nie istnieje, w zależności od tego odcinka.
Ogólnie, funkcja ciągła może nie osiągać kresów na
zbiorze niezwartym, w szczególności na podzbiorze otwartym
przyjmiemy odcinek otwarty, to minimum globalne
istnieje lub nie istnieje, w zależności od tego odcinka.
Ogólnie, funkcja ciągła może nie osiągać kresów na
zbiorze niezwartym, w szczególności na podzbiorze otwartym
![]() .
.
1.2. Istnienie minimum funkcji ciągłej
Przypomnijmy, że podzbiór zwarty w ![]() to podzbiór domknięty i ograniczony.
to podzbiór domknięty i ograniczony.
Twierdzenie 1.1
Jeśli ![]() jest zbiorem zwartym i
jest zbiorem zwartym i ![]() jest funkcją ciągłą, to
jest funkcją ciągłą, to ![]() osiąga kresy na
osiąga kresy na ![]() (dolny i górny).
Oznacza to, że istnieją
(dolny i górny).
Oznacza to, że istnieją ![]() ,
, ![]() takie, że dla dowolnego
takie, że dla dowolnego ![]() zachodzi
zachodzi
Będziemy oznaczali normę euklidesową w ![]() przez
przez
Warunek zwartości zbioru w powyższym twierdzeniu możemy osłabić do warunku domkniętości, jeśli funkcja jest koercywna. Koercywność funkcji definiujemy następująco:
Definicja 1.3
Funkcję ![]() na podzbiorze
na podzbiorze ![]() nazywamy koercywną, jeśli
nazywamy koercywną, jeśli ![]() dla
dla ![]() . Można ten warunek zapisać równoważnie
. Można ten warunek zapisać równoważnie
W szczególności, jeśli ![]() jest ograniczony, to
jest ograniczony, to ![]() jest automatycznie koercywna na
jest automatycznie koercywna na ![]() .
.
Twierdzenie 1.2
Jeśli zbiór ![]() jest domknięty oraz funkcja
jest domknięty oraz funkcja ![]() jest ciągła i koercywna, to istnieje punkt
jest ciągła i koercywna, to istnieje punkt ![]() w którym funkcja
w którym funkcja ![]() przyjmuje minimum, tzn. istnieje
przyjmuje minimum, tzn. istnieje ![]() taki, że
taki, że ![]() .
.
Dowód
Niech ![]() będzie ustalonym punktem w zbiorze
będzie ustalonym punktem w zbiorze ![]() . Rozpatrzmy zbiór
. Rozpatrzmy zbiór ![]() . Zauważmy, że
. Zauważmy, że ![]() jest zbiorem domkniętym w
jest zbiorem domkniętym w ![]() , bo funkcja
, bo funkcja ![]() jest ciągła, a nierówność w warunku nieostra. Z domkniętości
jest ciągła, a nierówność w warunku nieostra. Z domkniętości ![]() wynika, że
wynika, że ![]() jest domknięty w
jest domknięty w
![]() . Jest on też ograniczony. Mianowicie, dla
. Jest on też ograniczony. Mianowicie, dla ![]() , z koercywności
, z koercywności ![]() istnieje
istnieje ![]() takie, że jeśli
takie, że jeśli ![]() ,
to
,
to ![]() , skąd
, skąd ![]() jest zawarte w kuli
jest zawarte w kuli ![]() . Zatem
. Zatem ![]() jest zbiorem zwartym. Wówczas istnieje
jest zbiorem zwartym. Wówczas istnieje ![]() – punkt minimum na zbiorze
– punkt minimum na zbiorze ![]() . Dla
. Dla ![]() mamy
mamy ![]() , więc
, więc ![]() jest globalnym minimum na całym
jest globalnym minimum na całym ![]() .
.
Domkniętość ![]() nie jest potrzebna, jeśli
nie jest potrzebna, jeśli ![]() odpowiednio rośnie w pobliżu granicy
odpowiednio rośnie w pobliżu granicy ![]() .
.
Twierdzenie 1.3
Niech ![]() będzie dowolnym niepustym
podzbiorem oraz
będzie dowolnym niepustym
podzbiorem oraz ![]() – funkcją ciągłą. Jeśli dla pewnego ustalonego punktu
– funkcją ciągłą. Jeśli dla pewnego ustalonego punktu ![]() oraz dowolnego ciągu
oraz dowolnego ciągu ![]() , takiego że
, takiego że
zachodzi
to istnieje punkt ![]() w którym funkcja
w którym funkcja ![]() przyjmuje minimum.
przyjmuje minimum.
Dowód
Zbiór ![]() definiujemy jak w poprzednim dowodzie,
definiujemy jak w poprzednim dowodzie, ![]() . Aby pokazać domkniętość
. Aby pokazać domkniętość
![]() weźmy dowolny ciąg
weźmy dowolny ciąg ![]() zbieżny do
zbieżny do ![]() . Pokażemy, że
. Pokażemy, że ![]() . Z
. Z ![]() mamy
mamy ![]() i
jeśli
i
jeśli ![]() , nierówność ta przeczy założeniu twierdzenia. Wynika stąd, że
, nierówność ta przeczy założeniu twierdzenia. Wynika stąd, że ![]() . Korzystając teraz z
ciągłości
. Korzystając teraz z
ciągłości ![]() na
na ![]() dostajemy
dostajemy ![]() , skąd
, skąd ![]() . Ograniczoność zbioru
. Ograniczoność zbioru ![]() wynika z założonej w
twierdzeniu implikacji
wynika z założonej w
twierdzeniu implikacji ![]() . Pozostała część dowodu jest identyczna jak
w dowodzie poprzedniego twierdzenia.
. Pozostała część dowodu jest identyczna jak
w dowodzie poprzedniego twierdzenia.
Przykład 1.2
Funkcja ![]() jest ciągła i spełnia
założenia Twierdzenia 1.3 na zbiorze
jest ciągła i spełnia
założenia Twierdzenia 1.3 na zbiorze ![]() , osiąga więc minimum na
, osiąga więc minimum na ![]() .
.
1.3. Minima lokalne funkcji jednej zmiennej
Niech ![]() - podzbiór otwarty. Przypomnimy elementarne fakty.
- podzbiór otwarty. Przypomnimy elementarne fakty.
Twierdzenie 1.4 (Warunek konieczny I rzędu)
Jeśli ![]() jest punktem lokalnego minimum lub maksimum funkcji
jest punktem lokalnego minimum lub maksimum funkcji ![]() oraz
oraz ![]() posiada pochodną w punkcie
posiada pochodną w punkcie ![]() , to
, to
Dowód twierdzenia 1.4
Niech ![]() - minimum lokalne. Dla dostatecznie małych
- minimum lokalne. Dla dostatecznie małych ![]() zachodzi
zachodzi ![]() . Zatem dla
. Zatem dla ![]() mamy
mamy
Dla ![]()
Stąd ![]() .
.
Twierdzenie 1.5 (Warunek konieczny II rzędu)
Jeśli ![]() jest klasy
jest klasy ![]() na zbiorze
na zbiorze ![]() i
i ![]() jest punktem lokalnego minimum, to
jest punktem lokalnego minimum, to
Twierdzenie 1.6 (Warunek dostateczny II rzędu)
Jeśli ![]() jest klasy
jest klasy ![]() na zbiorze W oraz
na zbiorze W oraz ![]() ,
, ![]() dla pewnego
dla pewnego ![]() , to
, to ![]() ma ścisłe
lokalne minimum w punkcie
ma ścisłe
lokalne minimum w punkcie ![]() .
.
Uwaga 1.1
Twierdzenie 1.5 pozostaje prawdziwe przy zamianie lokalnego minimum na maksimum, jeśli znak znak drugiej pochodnej zmienimy na przeciwny.
Uwaga 1.2
Jeśli ![]() nie jest otwarty, to Twierdzenia 1.4 i 1.5 nie są prawdziwe dla
nie jest otwarty, to Twierdzenia 1.4 i 1.5 nie są prawdziwe dla ![]() (brzeg
(brzeg ![]() ), np. funkcja
), np. funkcja ![]() przyjmuje minimum na odcinku
przyjmuje minimum na odcinku ![]() w punkcie
w punkcie ![]() , ale żaden z warunków koniecznych tych twierdzeń nie zachodzi. Natomiast Twierdzenie 1.6 zachodzi również dla
, ale żaden z warunków koniecznych tych twierdzeń nie zachodzi. Natomiast Twierdzenie 1.6 zachodzi również dla ![]() będącego odcinkiem domkniętym i
będącego odcinkiem domkniętym i ![]() .
.
Poniższe twierdzenie uogólnia warunek dostateczny II rzędu.
Twierdzenie 1.7
Jeśli funkcja ![]() jest klasy
jest klasy ![]() na podzbiorze otwartym
na podzbiorze otwartym ![]() i zachodzi
i zachodzi ![]() oraz
oraz ![]() w pewnym
w pewnym ![]() , to:
, to:
I) Jeśli
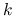 jest nieparzyste, to funkcja
jest nieparzyste, to funkcja 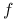 nie posiada w punkcie
nie posiada w punkcie 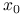 ekstremum
lokalnego.
ekstremum
lokalnego.II) Jeśli
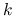 jest parzyste oraz:
jest parzyste oraz:(a)
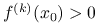 , to punkt
, to punkt 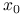 jest ścisłym minimum lokalnym
jest ścisłym minimum lokalnym 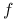 ,
,(b)
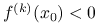 , to punkt
, to punkt 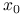 jest ścisłym maksimum lokalnym
jest ścisłym maksimum lokalnym 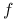 .
.
1.4. Wzory Taylora
W tym podrozdziale przypomnimy wyniki, których będziemy używać w wielu dowodach w trakcie tego wykładu. Skorzystamy z nich również, aby przedstawić zwięzłe dowody twierdzeń 1.5-1.7.
Twierdzenie 1.8 (Twierdzenie o wartości średniej)
Jeśli funkcja ![]() jest ciągła na
jest ciągła na ![]() i różniczkowalna na
i różniczkowalna na ![]() , to istnieje taki punkt
, to istnieje taki punkt ![]() , że
, że
Zauważmy, że do prawdziwości powyższego twierdzenia nie jest konieczna ciągłość pierwszej pochodnej (w zadaniu 1.7 pokazujemy, że różnicznowalność nie musi pociągać ciągłości pochodnej).
Dowód twierdzenia 1.8
Niech ![]() dla
dla ![]() . Wówczas
. Wówczas ![]() jest ciągła na
jest ciągła na ![]() , różniczkowalna w
, różniczkowalna w ![]() oraz
oraz
Pokażemy teraz, że istnieje punkt ![]() , w którym pochodna
, w którym pochodna ![]() się zeruje. Jeśli
się zeruje. Jeśli ![]() jest funkcją stałą, to dla dowolnego
jest funkcją stałą, to dla dowolnego ![]() mamy
mamy ![]() . W przeciwnym przypadku, na mocy twierdzenia 1.1 funkcja
. W przeciwnym przypadku, na mocy twierdzenia 1.1 funkcja ![]() przyjmuje swoje kresy na
przyjmuje swoje kresy na ![]() . Jeden z kresów jest różny od
. Jeden z kresów jest różny od ![]() . Zatem jest on przyjmowany w punkcie
. Zatem jest on przyjmowany w punkcie ![]() we wnętrzu przedziału
we wnętrzu przedziału ![]() . Korzystając z twierdzenia 1.4 wnioskujemy, że
. Korzystając z twierdzenia 1.4 wnioskujemy, że ![]() . Różniczkując
. Różniczkując ![]() otrzymujemy:
otrzymujemy:
Po prostych przekształceniach otrzymujemy poszukiwany wzór.
∎Twierdzenie 1.9 (Twierdzenie Taylora z resztą w postaci Peano)
Niech ![]() będzie funkcją klasy
będzie funkcją klasy ![]() na
na ![]() oraz dwukrotnie różniczkowalna w pewnym
oraz dwukrotnie różniczkowalna w pewnym ![]() . Wówczas dla
. Wówczas dla ![]() zachodzi następujący wzór:
zachodzi następujący wzór:
Uwaga 1.3
W sformułowaniu powyższego twierdzenia użyliśmy notacji małe o. Rozumieć ją należy następująco:
jest rządu mniejszego niż ![]() , tzn.
, tzn.
Przykład 1.3
Innym zastosowaniem powyższej notacji jest definicja pochodnej. Pochodną funkcji ![]() w punkcie
w punkcie ![]() nazywamy taką liczbę
nazywamy taką liczbę ![]() , że
, że
Dowód twierdzenia 1.9
Bez straty ogólności możemy założyć ![]() . Musimy wykazać, że
. Musimy wykazać, że ![]() jest niższego rzędu niż
jest niższego rzędu niż ![]() , tzn.
, tzn. ![]() . Z ciągłości pierwszej pochodnej
. Z ciągłości pierwszej pochodnej ![]() dostajemy
dostajemy
Wiemy, że ![]() jest różniczkowalna w
jest różniczkowalna w ![]() . Zatem
. Zatem ![]() , gdzie
, gdzie ![]() . Oznacza to, że
. Oznacza to, że
Dla dowolnego ![]() istnieje zatem
istnieje zatem ![]() , taka że
, taka że ![]() pociąga
pociąga ![]() .
.
Ustalmy zatem dowolny ![]() i związaną z nim
i związaną z nim ![]() . Weźmy
. Weźmy ![]() i scałkujmy pochodną
i scałkujmy pochodną ![]() . Otrzymamy wówczas:
. Otrzymamy wówczas:
czyli ![]() . Korzystając z oszacowania
. Korzystając z oszacowania ![]() dla
dla ![]() dostajemy
dostajemy
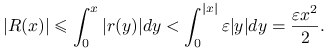 |
A zatem
Z dowolności ![]() wynika, iż
wynika, iż ![]() .
.
Uwaga 1.4
Twierdzenie 1.9 można uogólnić do dowolnie długiej aproksymacji Taylora. Dowód przebiega wówczas podobnie, lecz jest nieznacznie dłuższy.
Zakładając większą gładkość funkcji ![]() możemy opisać dokładniej błąd aproksymacji we wzorze Taylora.
możemy opisać dokładniej błąd aproksymacji we wzorze Taylora.
Twierdzenie 1.10 (Twierdzenie Taylora z resztą w postaci Lagrange'a)
Niech ![]() będzie funkcją klasy
będzie funkcją klasy ![]() na
na ![]() oraz
oraz ![]() -krotnie różniczkowalna na
-krotnie różniczkowalna na ![]() . Wtedy dla ustalonego
. Wtedy dla ustalonego ![]() i
i ![]() zachodzi następujący wzór:
zachodzi następujący wzór:
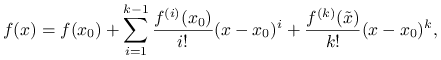 |
gdzie ![]() jest pewnym punktem pomiędzy
jest pewnym punktem pomiędzy ![]() i
i ![]() .
.
W szczególności dla ![]() dostajemy
dostajemy
Dowód twierdzenia 1.10
Niech liczba ![]() spełnia równanie
spełnia równanie
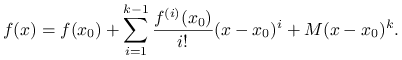 |
Celem dowodu jest pokazanie, że ![]() dla pewnego punktu
dla pewnego punktu ![]() pomiędzy
pomiędzy ![]() i
i ![]() . Określmy funkcję
. Określmy funkcję
![g(y)=f(y)-\sum _{{i=1}}^{{k-1}}\frac{f^{{(i)}}(x_{0})}{i!}(y-x_{0})^{i}-M(y-x_{0})^{k},\qquad y\in[x_{0},x].](wyklady/op2/mi/mi148.png) |
Zauważmy, że
Ponieważ ![]() , to na podstawie twierdzenia 1.8 istnieje
, to na podstawie twierdzenia 1.8 istnieje ![]() , taki że
, taki że ![]() . Stosując jeszcze raz tw. 1.8 do funkcji
. Stosując jeszcze raz tw. 1.8 do funkcji ![]() dla
dla ![]() dostajemy
dostajemy ![]() , w którym
, w którym ![]() . Postępując w ten sposób dostajemy ciąg punktów
. Postępując w ten sposób dostajemy ciąg punktów ![]() , takich że
, takich że ![]() ,
, ![]() . Z warunku dla punktu
. Z warunku dla punktu ![]() otrzymujemy
otrzymujemy
Szukanym punktem ![]() w twierdzeniu jest więc
w twierdzeniu jest więc ![]() .
.
1.5. Dowody twierdzeń 1.5-1.7
Dowód twierdzenia 1.5
Z twierdzenia 1.4 wiemy, że jeśli ![]() jest punktem minimum to
jest punktem minimum to ![]() Zatem korzystając ze wzoru Taylora, tw. 1.10, uzyskujemy
Zatem korzystając ze wzoru Taylora, tw. 1.10, uzyskujemy
dla pewnego punktu ![]() leżącego pomiędzy
leżącego pomiędzy ![]() i
i ![]() .
Z założenia, że
.
Z założenia, że ![]() jest minimum lokalnym, otrzymujemy
jest minimum lokalnym, otrzymujemy ![]() . Stąd i z
. Stąd i z ![]() wnioskujemy, że
wnioskujemy, że
Jeśli ![]() , to również
, to również ![]() . Wykorzystując ciągłość
. Wykorzystując ciągłość ![]() dostajemy
dostajemy ![]() .
.
Dowód twierdzenia 1.6
Z ciągłości drugiej pochodnej ![]() wynika, że istnieje kula
wynika, że istnieje kula ![]() , na której
, na której ![]() . Zatem dla
. Zatem dla ![]() ,
, ![]() , wnioskujemy ze wzoru Taylora, tw. 1.10, że
, wnioskujemy ze wzoru Taylora, tw. 1.10, że ![]() :
:
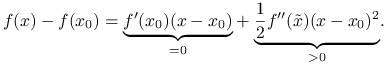 |
Oznacza to, że ![]() ma ścisłe minimum lokalne w
ma ścisłe minimum lokalne w ![]() .
.
Dowód twierdzenia 1.7
Z ciągłości ![]() i otwartości
i otwartości ![]() wynika, że istnieje kula
wynika, że istnieje kula ![]() , na której
, na której ![]() jest niezerowa (tzn.
jest niezerowa (tzn. ![]() nie zmienia znaku z ciągłości). Korzystając ze wzoru Taylora, tw. 1.10 i z założeń twierdzenia otrzymujemy
nie zmienia znaku z ciągłości). Korzystając ze wzoru Taylora, tw. 1.10 i z założeń twierdzenia otrzymujemy
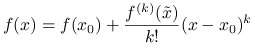 |
dla dowolnego ![]() oraz
oraz ![]() , zależnego od
, zależnego od ![]() , należącego do przedziału o końcach
, należącego do przedziału o końcach ![]() i
i ![]() .
Aby zbadać, czy zachodzi jedna z nierówności
.
Aby zbadać, czy zachodzi jedna z nierówności ![]() lub
lub ![]() dla wszystkich
dla wszystkich ![]() ,
, ![]() należy zbadać znak członu z potęgą
należy zbadać znak członu z potęgą ![]() . Człon ten zmienia znak dla
. Człon ten zmienia znak dla ![]() nieparzystego, stąd teza (I). Dla
nieparzystego, stąd teza (I). Dla ![]() parzystego znak różnicy
parzystego znak różnicy ![]() zależy od znaku pochodnej
zależy od znaku pochodnej ![]() na
na ![]() .
.
1.6. Ekstrema globalne
Uzupełnimy jeszcze twierdzenie 1.6 o wynik dotyczący ekstremów globalnych.
Niech ![]() będzie odcinkiem otwartym, domkniętym, lub jednostronnie domkniętym (być może nieograniczonym) i niech
będzie odcinkiem otwartym, domkniętym, lub jednostronnie domkniętym (być może nieograniczonym) i niech ![]() będzie funkcją klasy
będzie funkcją klasy ![]() na
na ![]() i klasy
i klasy ![]() na
na ![]() . Zachodzi następujące
. Zachodzi następujące
Twierdzenie 1.11
Przy powyższych założeniach, jeśli ![]() oraz:
oraz:
(a)
 jest globalnym minimum na
jest globalnym minimum na 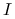 ,
,(b)
 jest globalnym maksimum na
jest globalnym maksimum na 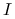 .
.
Jeśli założenia powyższe uzupełnimy o warunek ![]() (odpowiednio
(odpowiednio ![]() ), to
), to ![]() będzie ścisłym
globalnym minimum (maksimum).
będzie ścisłym
globalnym minimum (maksimum).
Dowód
Wzór Taylora, tw. 1.10, daje
gdzie ![]() jest pewnym punktem pomiędzy
jest pewnym punktem pomiędzy ![]() i
i ![]() . Stąd drugi człon wzoru Taylora decyduje o nierówności pomiędzy
. Stąd drugi człon wzoru Taylora decyduje o nierówności pomiędzy ![]() a
a ![]() i otrzymujemy obie implikacje w twierdzeniu dotyczące słabych ekstremów.
i otrzymujemy obie implikacje w twierdzeniu dotyczące słabych ekstremów.
Załóżmy dodatkowo w pierwszym stwierdzeniu, że ![]() . Z założenia
. Z założenia ![]() i warunku
i warunku ![]() dostajemy
dostajemy
gdy ![]() . Podobnie pokazujemy, że
. Podobnie pokazujemy, że ![]() , gdy
, gdy ![]() . Z faktu, że
. Z faktu, że
![]() i ciągłości drugiej pochodnej dostajemy dodatkowo, że ta pochodna jest ściśle dodatnia w otoczeniu
i ciągłości drugiej pochodnej dostajemy dodatkowo, że ta pochodna jest ściśle dodatnia w otoczeniu ![]() . Zatem
całki są dodatnie, co pociąga nierówności
. Zatem
całki są dodatnie, co pociąga nierówności ![]() , gdy
, gdy ![]() , oraz
, oraz ![]() , gdy
, gdy ![]() . Wynika stąd, że funkcja
. Wynika stąd, że funkcja ![]() jest ściśle rosnąca na prawo od
jest ściśle rosnąca na prawo od ![]() i ściśle malejąca na lewo od
i ściśle malejąca na lewo od ![]() , a więc
, a więc ![]() jest ścisłym minimum. Przypadek ścisłego maksimum dowodzimy analogicznie.
jest ścisłym minimum. Przypadek ścisłego maksimum dowodzimy analogicznie.
1.7. Zadania
Ćwiczenie 1.1
Czy funkcja ![]() osiąga minimum na zbiorze
osiąga minimum na zbiorze ![]() .
.
Ćwiczenie 1.2
Znajdź minimum funkcji ![]() na zbiorze
na zbiorze ![]()
Ćwiczenie 1.3
Znajdź maksimum funkcji ![]() na zbiorze
na zbiorze ![]()
Ćwiczenie 1.4
Znajdź minimum funkcji ![]() na zbiorze
na zbiorze ![]()
Ćwiczenie 1.5
Rozważmy następujący nieliniowy problem optymalizacyjny:
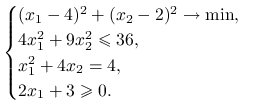 |
Naszkicuj zbiór punktów dopuszczalnych, czyli punktów spełniających wszystkie ograniczenia.
Znajdź graficznie rozwiązanie powyższego problemu optymalizacyjnego.
Znajdź następnie rozwiązanie w przypadku, gdy minimalizacja zamieniona zostanie na maksymalizację.
Ćwiczenie 1.6
Niech ![]() będzie funkcją spełniającą:
będzie funkcją spełniającą: ![]() ,
, ![]() , oraz
, oraz ![]() Znajdź
Znajdź ![]() , dla którego następująca całka jest minimalna:
, dla którego następująca całka jest minimalna:
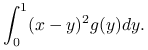 |
Ćwiczenie 1.7
Wykaż, że funkcja
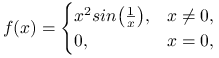 |
jest różniczkowalna w ![]() , lecz jej pochodna nie jest ciągła.
, lecz jej pochodna nie jest ciągła.
Ćwiczenie 1.8
Udowodnij, że poniższe definicje pochodnej funkcji ![]() w punkcie
w punkcie ![]() są równoważne:
są równoważne:
(a)
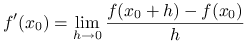 ,
,(b)
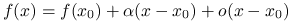 dla
dla ![x\in[a,b]](wyklady/op2/mi/mi145.png) i
i 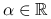 niezależnego od
niezależnego od 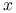 .
.
Przez równoważność rozumiemy to, że jeśli granica w (a) istnieje, to zależność (b) jest spełniona z ![]() ; i odwrotnie, jeśli (b) zachodzi dla pewnego
; i odwrotnie, jeśli (b) zachodzi dla pewnego ![]() , to granica w (a) istnieje i jest równa
, to granica w (a) istnieje i jest równa ![]() .
.




