11. Teoria wrażliwości
Dotychczas mnożniki Lagrange'a wydawały się techniczną sztuczką służącą do znajdowania rozwiązania problemu optymalizacyjnego z ograniczeniami. W tym rozdziale pokażemy, że pełnią one rolę kosztu związanego ze zmianą ograniczeń. Oddzielnie zajmiemy się ograniczeniami równościowymi i nierównościowymi.
11.1. Ograniczenia równościowe
Rozważmy problem optymalizacyjny z ograniczeniami równościowymi:
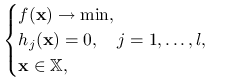 |
(11.1) |
gdzie ![]() jest zbiorem otwartym i
jest zbiorem otwartym i ![]() . Dla uproszczenia notacji połóżmy
. Dla uproszczenia notacji połóżmy ![]() . Rozważmy problem zaburzony, tzn.
. Rozważmy problem zaburzony, tzn.
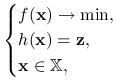 |
(11.2) |
gdzie ![]()
Twierdzenie 11.1
Niech ![]() będzie rozwiązaniem lokalnym problemu (11.1), zaś
będzie rozwiązaniem lokalnym problemu (11.1), zaś ![]() wektorem jego mnożników Lagrange'a. Załóżmy, że funkcje
wektorem jego mnożników Lagrange'a. Załóżmy, że funkcje ![]() są klasy
są klasy ![]() na otoczeniu
na otoczeniu ![]() , gradienty ograniczeń są liniowo niezależne (spełniony jest warunek liniowej niezależności) oraz
, gradienty ograniczeń są liniowo niezależne (spełniony jest warunek liniowej niezależności) oraz
| (11.3) |
dla ![]() spełniających
spełniających ![]() ,
, ![]() Wówczas istnieje otoczenie
Wówczas istnieje otoczenie ![]() punktu
punktu ![]() oraz funkcja
oraz funkcja ![]() klasy
klasy ![]() , taka że
, taka że ![]() oraz
oraz ![]() jest ścisłym rozwiązaniem lokalnym problemu zaburzonego (11.2). Ponadto,
jest ścisłym rozwiązaniem lokalnym problemu zaburzonego (11.2). Ponadto,
Dowód
Na mocy tw. 8.1 punkt ![]() rozwiązuje układ równań:
rozwiązuje układ równań:
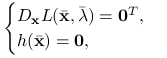 |
gdzie
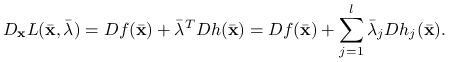 |
Zaburzając prawą stronę drugiej równości przez ![]() będziemy chcieli pokazać, że istnieje rozwiązanie, które jest funkcją
będziemy chcieli pokazać, że istnieje rozwiązanie, które jest funkcją ![]() klasy
klasy ![]() . Rozważmy więc układ:
. Rozważmy więc układ:
gdzie niewiadomymi są ![]() oraz
oraz ![]() .
Zdefiniujmy funkcję
.
Zdefiniujmy funkcję ![]() wzorem
wzorem
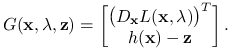 |
Zaburzony układ możemy wówczas zapisać jako
Wiemy, że ![]() Skorzystamy z twierdzenia o funkcji uwikłanej, aby rozwikłać pierwsze dwie zmienne w zależności od trzeciej. W tym celu rozważamy macierz pochodnych
Skorzystamy z twierdzenia o funkcji uwikłanej, aby rozwikłać pierwsze dwie zmienne w zależności od trzeciej. W tym celu rozważamy macierz pochodnych ![]() :
:
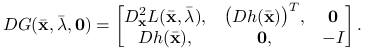 |
Warunek liniowej niezależności gradientów ograniczeń implikuje nieosobliwość podmacierzy
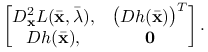 |
Spełnione są zatem założenia twierdzenia 8.4 i istnieje otoczenie ![]() punktu
punktu ![]() oraz funkcje
oraz funkcje ![]() i
i ![]() klasy
klasy ![]() , takie że dla
, takie że dla ![]() zachodzi
zachodzi ![]() , czyli
, czyli
Korzystając z faktu, iż funkcje ![]() są ciągłe oraz nierówność (11.3) spełniona jest dla niezaburzonego problemu, wnioskujemy, że istnieje być może mniejsze otoczenie
są ciągłe oraz nierówność (11.3) spełniona jest dla niezaburzonego problemu, wnioskujemy, że istnieje być może mniejsze otoczenie ![]() punktu
punktu ![]() , takie że
, takie że
dla ![]() i
i ![]() spełniających
spełniających ![]() ,
, ![]() Kluczowa dla tego wyniku jest ostra nierówność w warunku (11.3). Na mocy tw. 9.3 punkt
Kluczowa dla tego wyniku jest ostra nierówność w warunku (11.3). Na mocy tw. 9.3 punkt ![]() jest zatem ścisłym rozwiązaniem lokalnym problemu zaburzonego (11.2). Przypomnijmy, że funkcja
jest zatem ścisłym rozwiązaniem lokalnym problemu zaburzonego (11.2). Przypomnijmy, że funkcja ![]() jest klasy
jest klasy ![]() . Możemy zatem zdefiniować pochodną złożenia
. Możemy zatem zdefiniować pochodną złożenia
Od zakończenia dowodu dzielą nas dwa spostrzeżenia. Po pierwsze, mnożąc obie strony warunku koniecznego pierwszego rzędu dla problemu niezaburzonego
przez ![]() dostajemy
dostajemy
Po drugie, rózniczkując ![]() po
po ![]() otrzymujemy w punkcie
otrzymujemy w punkcie ![]() następującą pochodną
następującą pochodną ![]() , czyli
, czyli ![]() Upraszcza to powyższe równanie do
Upraszcza to powyższe równanie do
Stąd już teza wynika natychmiast.
∎Twierdzenie 11.1 można rozumieć następująco: nieznaczna zmiana ![]() -tego ograniczenia z zera do
-tego ograniczenia z zera do ![]() prowadzi do zmiany optymalnej wartości funkcji
prowadzi do zmiany optymalnej wartości funkcji ![]() o
o ![]() , tzn. dla małych
, tzn. dla małych ![]() zmiana ta jest w przybliżeniu równa
zmiana ta jest w przybliżeniu równa ![]()
11.2. Ograniczenia nierównościowe
W przypadku ograniczeń nierównościowych zastosujemy inne podejście. Skoncentrujemy się na zadaniu optymalizacji wypukłej:
 |
(11.4) |
gdzie ![]() jest wypukły,
jest wypukły, ![]() są wypukłe. Dla uproszczenia notacji będziemy pisać
są wypukłe. Dla uproszczenia notacji będziemy pisać ![]() . Problem (11.4) zapisujemy więc jako
. Problem (11.4) zapisujemy więc jako
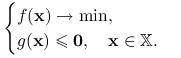 |
(11.5) |
Rozważmy zadanie zaburzone: dla ![]()
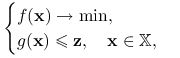 |
(11.6) |
Definicja 11.1
Niech ![]() będzie zbiorem takich
będzie zbiorem takich ![]() , dla których zbiór punktów dopuszczalnych
, dla których zbiór punktów dopuszczalnych ![]() jest niepusty.
Funkcją perturbacji nazywamy funkcję
jest niepusty.
Funkcją perturbacji nazywamy funkcję
określoną dla ![]() należących do dziedziny
należących do dziedziny ![]() .
.
Zauważmy, że ![]() dla
dla ![]() , ale może się zdarzyć, że
, ale może się zdarzyć, że ![]() .
.
Twierdzenie 11.2
![]()
Zbiór
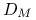 jest wypukły.
jest wypukły.Funkcja
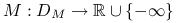 jest wypukła.
jest wypukła.Jeśli istnieje punkt
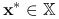 , taki że
, taki że 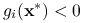 ,
, 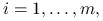 to
to 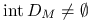 i
i 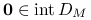 .
.
Dowód
Z wypukłości ![]() wynika następująca implikacja:
wynika następująca implikacja:
| (11.7) |
Będziemy korzystać z tego spostrzeżenia wielokrotnie w dowodzie.
(1) Niech ![]() i
i ![]() Wówczas istnieją
Wówczas istnieją ![]() takie że
takie że ![]() i
i ![]() Z wzoru (11.7) dostajemy
Z wzoru (11.7) dostajemy ![]() , skąd wynika
, skąd wynika ![]()
(2) Niech ![]() i
i ![]() Wówczas
Wówczas
gdzie pierwsza nierówność wynika z wypukłości ![]() , zaś ostatnia – z własności (11.7):
, zaś ostatnia – z własności (11.7):
(3) Musimy udowodnić, że zbiór dopuszczalny ![]() jest niepusty dla
jest niepusty dla ![]() z pewnego otoczenia
z pewnego otoczenia ![]() . Wiemy, że istnieje punkt
. Wiemy, że istnieje punkt ![]() , taki że
, taki że ![]() ,
, ![]() Weźmy
Weźmy ![]() Wówczas dla każdego
Wówczas dla każdego ![]() mamy
mamy ![]() Zatem
Zatem ![]() .
.
Uwaga 11.1
Jeśli
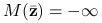 dla pewnego
dla pewnego 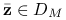 , to dla dowolnego
, to dla dowolnego 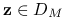 i
i 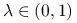 mamy z wypukłości
mamy z wypukłości 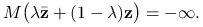
Jeśli
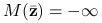 dla pewnego
dla pewnego 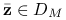 , to
, to 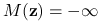 dla
dla 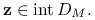 Wynika to wprost z powyższej uwagi.
Wynika to wprost z powyższej uwagi.Jeśli istnieje
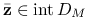 taki że
taki że 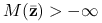 , to
, to 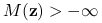 dla każdego
dla każdego 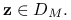 Inaczej mielibyśmy sprzeczność z punktem (2).
Inaczej mielibyśmy sprzeczność z punktem (2).
Twierdzenie 11.3
Jeśli w problemie optymalizacji wypukłej istnieje punkt ![]() , taki że
, taki że ![]() ,
, ![]() oraz
oraz ![]() , to
, to ![]() dla każdego
dla każdego ![]() oraz istnieje wektor
oraz istnieje wektor ![]() wyznaczający płaszczyznę podpierającą
wyznaczający płaszczyznę podpierającą ![]() :
:
Dowód
Z tw. 11.2 wynika, że ![]() jest funkcją wypukłą i
jest funkcją wypukłą i ![]() Zatem na mocy ostatniej z powyższych uwag mamy
Zatem na mocy ostatniej z powyższych uwag mamy ![]() dla
dla ![]() Istnienie płaszczyzny podpierającej wynika z tw. 3.8:
Istnienie płaszczyzny podpierającej wynika z tw. 3.8:
dla pewnego ![]() Udowodnimy teraz, że wszystkie współrzędne
Udowodnimy teraz, że wszystkie współrzędne ![]() muszą być nieujemne. Przypuśćmy przeciwnie, tzn.
muszą być nieujemne. Przypuśćmy przeciwnie, tzn. ![]() dla pewnego
dla pewnego ![]() Ponieważ
Ponieważ ![]() , to dla dostatecznie małego
, to dla dostatecznie małego ![]() punkt
punkt ![]() , gdzie
, gdzie ![]() jest na
jest na ![]() -tej pozycji, należy do
-tej pozycji, należy do ![]() . Korzystając z ujemności
. Korzystając z ujemności ![]() mamy
mamy
Z drugiej strony ![]() , czyli
, czyli ![]() To daje sprzeczność, czyli dowiedliśmy, że
To daje sprzeczność, czyli dowiedliśmy, że ![]()
Wektor ![]() nazywamy wektorem wrażliwości dla problemu (11.4). Z tw. 3.8 wynika, że jeśli funkcja
nazywamy wektorem wrażliwości dla problemu (11.4). Z tw. 3.8 wynika, że jeśli funkcja ![]() jest różniczkowalna w punkcie
jest różniczkowalna w punkcie ![]() , to
, to ![]() Zatem
Zatem ![]() oznacza szybkość i kierunek zmian wartości minimalnej
oznacza szybkość i kierunek zmian wartości minimalnej ![]() przy zmianie ograniczeń, podobnie jak w przypadku ograniczeń równościowych omawianych wcześniej w tym rozdziale.
przy zmianie ograniczeń, podobnie jak w przypadku ograniczeń równościowych omawianych wcześniej w tym rozdziale.
Zbadajmy teraz relacje pomiędzy wektorem wrażliwości a punktem siodłowym i warunkiem pierwszego rzędu. Zauważmy, że powiązanie punktu siodłowego z wektorem wrażliwości nie wymaga wypukłości problemu optymalizacyjnego.
Twierdzenie 11.4
Jeśli
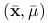 jest punktem siodłowym funkcji Lagrange'a na zbiorze
jest punktem siodłowym funkcji Lagrange'a na zbiorze 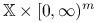 , to
, to 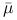 jest wektorem wrażliwości (tzn. wyznacza płaszczyznę podpierającą). Teza ta nie wymaga założenia o wypukłości problemu optymalizacyjnego.
jest wektorem wrażliwości (tzn. wyznacza płaszczyznę podpierającą). Teza ta nie wymaga założenia o wypukłości problemu optymalizacyjnego.Załóżmy, że funkcje
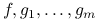 są różniczkowalne w
są różniczkowalne w 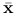 , i wypukłe. Jeśli w
, i wypukłe. Jeśli w 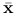 spełniony jest warunek pierwszego rzędu z mnożnikami Lagrange'a
spełniony jest warunek pierwszego rzędu z mnożnikami Lagrange'a 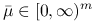 , to
, to 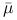 jest wektorem wrażliwości.
jest wektorem wrażliwości.
Dowód
(1) Oznaczmy przez ![]() funkcję Langrange'a dla problemu zaburzonego. Wówczas
funkcję Langrange'a dla problemu zaburzonego. Wówczas
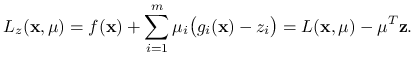 |
Z faktu, że ![]() jest punktem siodłowym wynika, że
jest punktem siodłowym wynika, że
Zatem
| (11.8) |
Zauważmy, że dla dowolnego ![]() i
i ![]() mamy
mamy ![]() czyli, w szczególności,
czyli, w szczególności,
Wstawiając tą zależność do (11.8) otrzymujemy
(2) Z zadania 10.1 wynika, iż punkt ![]() jest punktem siodłowym funkcji Lagrange'a. Tezę dostajemy z pierwszej części niniejszego twierdzenia.
jest punktem siodłowym funkcji Lagrange'a. Tezę dostajemy z pierwszej części niniejszego twierdzenia.
11.3. Zadania
Ćwiczenie 11.1
Dla problemu
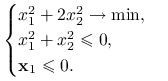 |
Znaleźć
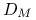 .
.Znaleźć wektor wrażliwości.
Znaleźć funkcję perturbacji.
Umieszczenie ograniczenia ![]() było intencją autora zadania.
było intencją autora zadania.
Ćwiczenie 11.2
Znajdź funkcję perturbacji i wektor wrażliwości dla problemu
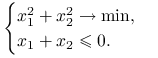 |
Ćwiczenie 11.3
Załóżmy, że w zadaniu optymalizacyjnym (11.4) funkcje ![]() i
i ![]() są klasy
są klasy ![]() oraz
oraz ![]() . Czy funkcja perturbacji musi być wówczas klasy
. Czy funkcja perturbacji musi być wówczas klasy ![]() ? Udowodnij lub podaj kontrprzykład.
? Udowodnij lub podaj kontrprzykład.
Ćwiczenie 11.4
Załóżmy, że w zadaniu optymalizacyjnym (11.4) funkcje ![]() i
i ![]() są ciągłe oraz
są ciągłe oraz ![]() . Czy funkcja perturbacji musi być wówczas ciągła? Udowodnij lub podaj kontrprzykład.
. Czy funkcja perturbacji musi być wówczas ciągła? Udowodnij lub podaj kontrprzykład.
Ćwiczenie 11.5
Rozważmy problem producenta. Dysponuje on budżetem ![]() , który może spożytkować na wytworzenie dwóch rodzajów towarów. Pierwszy z towarów sprzedaje po cenie
, który może spożytkować na wytworzenie dwóch rodzajów towarów. Pierwszy z towarów sprzedaje po cenie ![]() , zaś drugi – po cenie
, zaś drugi – po cenie ![]() Cena produkcji opisana jest funkcją
Cena produkcji opisana jest funkcją ![]() , gdzie wektor
, gdzie wektor ![]() opisuje wielkość produkcji każdego z towarów. Celem producenta jest maksymalizacja przychodów ze sprzedaży bez przekroczenia budżetu produkcyjnego:
opisuje wielkość produkcji każdego z towarów. Celem producenta jest maksymalizacja przychodów ze sprzedaży bez przekroczenia budżetu produkcyjnego:
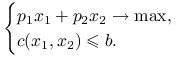 |
Podaj warunki konieczne istnienia rozwiązania powyższego problemu.
Załóżmy, że
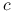 jest funkcją wypukłą. Jak należy zmodyfikować wielkość produkcji, jeśli budżet produkcyjny
jest funkcją wypukłą. Jak należy zmodyfikować wielkość produkcji, jeśli budżet produkcyjny 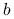 wrośnie nieznacznie?
wrośnie nieznacznie?
Ćwiczenie 11.6
Rozważmy funkcję ![]() zadaną wzorem
zadaną wzorem
Uzasadnij, że funkcja ![]() jest dobrze określona i wypukła.
jest dobrze określona i wypukła.




