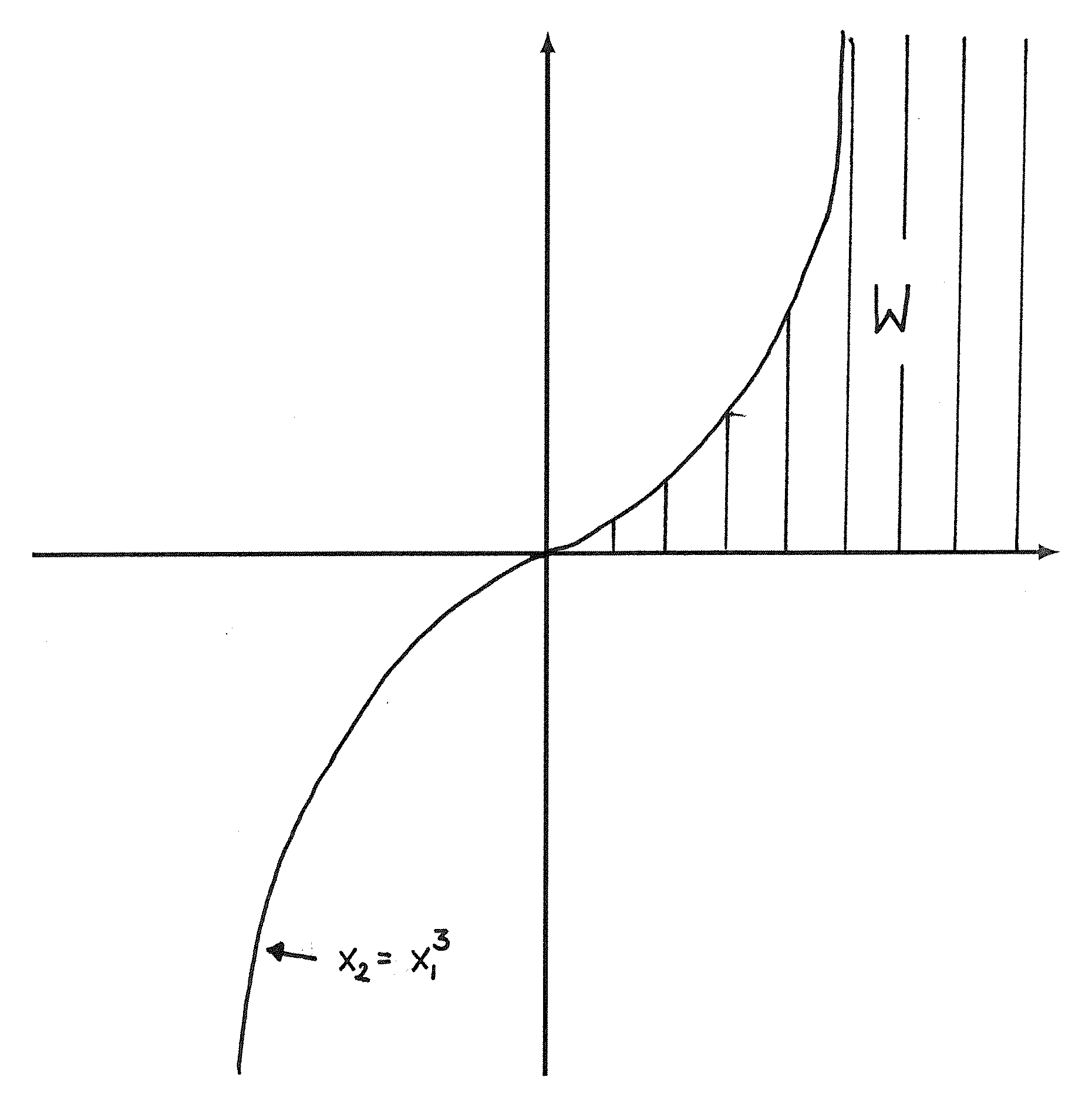Zagadnienia
6. Warunki regularności i przykłady
W tym rozdziale podamy warunki dostateczne równości stożka kierunków stycznych ![]() i stożka kierunków stycznych dla ograniczeń zlinearyzowanych
i stożka kierunków stycznych dla ograniczeń zlinearyzowanych ![]() . Przypomnijmy, że jest to główne założenie twierdzenia Kuhna-Tuckera, tw. 5.2, opisującego warunek konieczny pierwszego rzędu dla lokalnego rozwiązania problemu optymalizacyjnego z ograniczeniami nierównościowymi (5.3).
. Przypomnijmy, że jest to główne założenie twierdzenia Kuhna-Tuckera, tw. 5.2, opisującego warunek konieczny pierwszego rzędu dla lokalnego rozwiązania problemu optymalizacyjnego z ograniczeniami nierównościowymi (5.3).
6.1. Warunki regularności
Sformułujemy teraz trzy warunki dostateczne równości ![]() , zwane warunkami regularności. Dowody dostateczności podamy w kolejnych twierdzeniach.
, zwane warunkami regularności. Dowody dostateczności podamy w kolejnych twierdzeniach.
Definicja 6.1
W punkcie ![]() spełniony jest:
spełniony jest:
warunek liniowej niezależności, jeśli funkcje
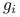 ,
, 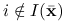 , są ciągłe w
, są ciągłe w  oraz wektory
oraz wektory 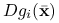 , dla
, dla 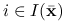 , są liniowo niezależne,
, są liniowo niezależne,warunek afiniczności, jeśli funkcje
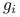 ,
, 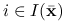 , są afiniczne oraz funkcje
, są afiniczne oraz funkcje 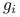 ,
, 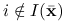 , są ciągłe w
, są ciągłe w  ,
,warunek Slatera, jeśli funkcje
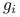 ,
, 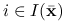 są pseudowypukłe w
są pseudowypukłe w  , funkcje
, funkcje 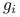 ,
, 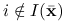 , są ciągłe w
, są ciągłe w  oraz istnieje
oraz istnieje 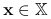 , dla którego
, dla którego 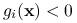 dla
dla 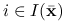 .
.
Zauważmy, że w warunku Slatera nie wymagamy, aby punkt ![]() spełniał warunki ograniczeń nieaktywnych, tzn.
spełniał warunki ograniczeń nieaktywnych, tzn. ![]() nie musi być w zbiorze
nie musi być w zbiorze ![]() .
.
Twierdzenie 6.1
Jeśli w punkcie ![]() spełniony jest warunek afiniczności, to
spełniony jest warunek afiniczności, to ![]() .
.
Dowód
Zawieranie ![]() wynika z lematu 5.2. Wystarczy zatem wykazać zawieranie w drugą stronę.
wynika z lematu 5.2. Wystarczy zatem wykazać zawieranie w drugą stronę.
Niech ![]() . Udowodnimy, że istnieje
. Udowodnimy, że istnieje ![]() , taka że cały odcinek
, taka że cały odcinek ![]() ,
, ![]() , zawarty jest w
, zawarty jest w ![]() :
:
| (6.1) |
Zauważmy, że ![]() dla
dla ![]() . Z ciągłości tych funkcji w
. Z ciągłości tych funkcji w ![]() wynika, że istnieje
wynika, że istnieje ![]() , dla której
, dla której ![]() ,
, ![]() ,
, ![]() . Pozostaje jeszcze wykazać, że nierówność taka zachodzi dla ograniczeń aktywnych. Ustalmy
. Pozostaje jeszcze wykazać, że nierówność taka zachodzi dla ograniczeń aktywnych. Ustalmy ![]() . Z definicji
. Z definicji ![]() wiemy, że
wiemy, że ![]() . Ograniczenie
. Ograniczenie ![]() jest afiniczne, czyli postaci
jest afiniczne, czyli postaci ![]() , gdzie
, gdzie ![]() ,
, ![]() . Zatem
. Zatem ![]() . Z faktu, że
. Z faktu, że ![]() jest aktywne w
jest aktywne w ![]() dostajemy również
dostajemy również ![]() . Stąd dla dowolnego
. Stąd dla dowolnego ![]() mamy
mamy
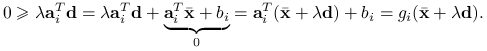 |
Dowodzi to (6.1).
Pozostaje już tylko skonstruować ciąg ![]() ,
, ![]() i
i ![]() . Kładziemy
. Kładziemy
Wówczas ![]() ,
, ![]() oraz
oraz ![]() , czyli trywialnie
, czyli trywialnie
a zatem ![]() .
.
Przed przystąpieniem do dowodu analogicznych twierdzeń dla pozostałych warunków regularności sformułujemy pomocniczy lemat. Wprowadźmy zbiór
Uwaga 6.1
Zauważmy, że jeśli w punkcie ![]() funkcje
funkcje ![]() ,
, ![]() , są różniczkowalne w
, są różniczkowalne w ![]() , zaś funkcje
, zaś funkcje ![]() ,
, ![]() są ciągłe w
są ciągłe w ![]() , to
, to ![]() oznacza, że
oznacza, że ![]() dla dostatecznie małych
dla dostatecznie małych ![]() .
.
Lemat 6.1
Niech ![]() oraz funkcje
oraz funkcje ![]() ,
, ![]() , są różniczkowalne w
, są różniczkowalne w ![]() , zaś funkcje
, zaś funkcje ![]() ,
, ![]() są ciągłe w
są ciągłe w ![]() .
Wówczas
.
Wówczas
I)
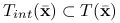 ,
,II) Jeśli
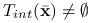 , to
, to 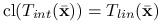 .
.
Dowód
Dowód (I) zostawiamy jako ćwiczenie. Do dowodu (II) zauważmy, że ![]() jest wnętrzem zbioru
jest wnętrzem zbioru ![]() . Ponadto
. Ponadto ![]() jest zbiorem wielościennym, a zatem wypukłym (patrz lemat 4.5). Zastosowanie lematu 3.2 kończy dowód.
jest zbiorem wielościennym, a zatem wypukłym (patrz lemat 4.5). Zastosowanie lematu 3.2 kończy dowód.
Twierdzenie 6.2
Jeśli w punkcie ![]() spełniony jest warunek Slatera, to
spełniony jest warunek Slatera, to ![]() .
.
Dowód
Pokażemy najpierw, że ![]() . Niech
. Niech ![]() taki że
taki że ![]() dla
dla ![]() . Z pseudowypukłości
. Z pseudowypukłości ![]() w punkcie
w punkcie ![]() dostajemy
dostajemy ![]() dla
dla ![]() , czyli
, czyli ![]() .
.
Na mocy lematu 6.1 mamy ![]() . Udowodniliśmy także, że
. Udowodniliśmy także, że ![]() oraz, że
oraz, że ![]() jest domknięty. A zatem
jest domknięty. A zatem ![]() .
.
Dowód analogicznego twierdzenia dla warunku liniowej niezależności wymaga pomocniczego lematu w stylu lematu Farkasa. Wynik ten jest jednak wcześniejszy i został uzyskany przez Paul'a Gordana w 1873 roku.
Lemat 6.2 (Gordan, 1873)
Niech ![]() będzie macierzą
będzie macierzą ![]() . Wówczas dokładnie jeden z układów ma rozwiązanie:
. Wówczas dokładnie jeden z układów ma rozwiązanie:
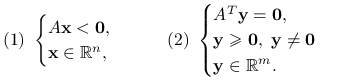 |
Dowód
Dowód rozpoczniemy od uzasadnienia, że oba te układy nie mogą mieć rozwiązania jednocześnie. Załóżmy więc przez sprzeczność, że istnieją ![]() spełniające (1)-(2). Z faktu, że
spełniające (1)-(2). Z faktu, że ![]() rozwiązuje (2), dostajemy, że
rozwiązuje (2), dostajemy, że ![]() . Z drugiej strony
. Z drugiej strony ![]() rozwiązuje (1), czyli
rozwiązuje (1), czyli ![]() dla każdego
dla każdego ![]() . Pamiętając, że
. Pamiętając, że ![]() ,
, ![]() , i
, i ![]() mamy
mamy ![]() . Dostaliśmy więc sprzeczność, co dowodzi, że nie może istnieć jednocześnie rozwiązanie (1) i (2).
. Dostaliśmy więc sprzeczność, co dowodzi, że nie może istnieć jednocześnie rozwiązanie (1) i (2).
Następnym krokiem dowodu będzie wykazanie, że zawsze któryś z układów ma rozwiązanie. W tym celu udowodnimy, że jeśli układ (1) nie ma rozwiązania, to układ (2) ma rozwiązanie. W tym celu zdefiniujmy następujące zbiory wypukłe:
Z faktu, że układ (1) nie ma rozwiązania, wynika, iż zbiory te są rozłączne. Słabe twierdzenie o oddzielaniu implikuje istnienie wektora ![]() ,
, ![]() , takiego że
, takiego że
Wykażemy, że ![]() . Przypuśćmy przeciwnie, że istnieje współrzędna
. Przypuśćmy przeciwnie, że istnieje współrzędna ![]() . Rozważmy ciąg
. Rozważmy ciąg ![]() , gdzie
, gdzie ![]() jest na
jest na ![]() -tej pozycji. Wówczas
-tej pozycji. Wówczas ![]() oraz
oraz ![]() , a zatem dostaliśmy sprzeczność, gdyż
, a zatem dostaliśmy sprzeczność, gdyż ![]() jest skończone.
jest skończone.
Wiemy zatem, że wektor ![]() ma wszystkie współrzędne nieujemne. Pociąga to
ma wszystkie współrzędne nieujemne. Pociąga to ![]() . Weźmy
. Weźmy ![]() . Wówczas
. Wówczas ![]() , czyli
, czyli ![]() . A zatem
. A zatem
co implikuje, że ![]() , czyli
, czyli ![]() . Rozwiązaniem układu (2) jest zatem
. Rozwiązaniem układu (2) jest zatem ![]() .
.
Twierdzenie 6.3
Jeśli w punkcie ![]() spełniony jest warunek liniowej niezależności, to
spełniony jest warunek liniowej niezależności, to ![]() .
.
Dowód
Identycznie jak w dowodzie tw. 6.2 wystarczy pokazać, że ![]() . Niech
. Niech ![]() będzie macierzą składającą się z gradientów
będzie macierzą składającą się z gradientów ![]() ograniczeń aktywnych (jako rzędów). Na mocy liniowej niezależności nie istnieje wektor
ograniczeń aktywnych (jako rzędów). Na mocy liniowej niezależności nie istnieje wektor ![]() ,
, ![]() , o tej własności, że
, o tej własności, że ![]() . Nie istnieje więc rozwiązanie układu (2) w lemacie 6.2. A zatem ma rozwiązanie układ (1), czyli istnieje
. Nie istnieje więc rozwiązanie układu (2) w lemacie 6.2. A zatem ma rozwiązanie układ (1), czyli istnieje ![]() , takie że
, takie że ![]() :
:
Stąd ![]() .
.
6.2. Przykłady
Przykład 6.1
Rozważmy problem optymalizacji na zbiorze:
Zbiór ![]() . Ograniczenia są opisane przez trójkę funkcji
. Ograniczenia są opisane przez trójkę funkcji
W punkcie ![]() wszystkie ograniczenia są aktywne i mamy
wszystkie ograniczenia są aktywne i mamy
Warunek liniowej niezależności ograniczeń nie jest spełniony w ![]() . Ograniczenia aktywne nie są również afiniczne. Pozostaje zatem sprawdzić warunek Slatera. Wszystkie funkcje ograniczeń są wypukłe, a więc także pseudowypukłe. W punkcie
. Ograniczenia aktywne nie są również afiniczne. Pozostaje zatem sprawdzić warunek Slatera. Wszystkie funkcje ograniczeń są wypukłe, a więc także pseudowypukłe. W punkcie ![]() mamy
mamy ![]() dla
dla ![]() . Zachodzi więc warunek Slatera.
. Zachodzi więc warunek Slatera.
Przykład 6.2 (Kuhn, Tucker (1951))
Rozważmy zadanie optymalizacyjne:
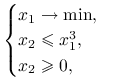 |
Zbiór punktów dopuszczalnych ![]() naszkicowany jest na rysunku 6.1. Zapiszmy funkcje opisujące ograniczenia:
naszkicowany jest na rysunku 6.1. Zapiszmy funkcje opisujące ograniczenia:
Zauważmy, że w każdym punkcie dopuszczalnym, poza ![]() , spełniony jest warunek liniowej niezależności. Widać jednak, że rozwiązaniem powyższego problemu optymalizacyjnego jest
, spełniony jest warunek liniowej niezależności. Widać jednak, że rozwiązaniem powyższego problemu optymalizacyjnego jest ![]() . Niestety w tym punkcie
. Niestety w tym punkcie ![]() :
:
Przykład 6.3
Niech ![]() będzie macierzą symetryczną
będzie macierzą symetryczną ![]() . Rozważmy zadanie optymalizacyjne:
. Rozważmy zadanie optymalizacyjne:
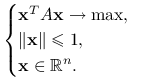 |
Zapiszmy najpierw problem optymalizacyjny w kanonicznej formie. Zauważmy przy tym, że warunek ![]() jest równoważny
jest równoważny ![]() .
.
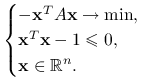 |
Oznaczmy przez ![]() zbiór punktów dopuszczalnych. Zauważmy, że w każdym punkcie dopuszczalnym spełnione są warunki liniowej niezależności i Slatera. Wynika stąd, że rozwiązanie powyższego zadania spełnia warunki konieczne pierwszego rzędu (warunki Kuhna-Tuckera (5.5)). Znajdziemy teraz wszystkie punkty ,,podejrzane”.
zbiór punktów dopuszczalnych. Zauważmy, że w każdym punkcie dopuszczalnym spełnione są warunki liniowej niezależności i Slatera. Wynika stąd, że rozwiązanie powyższego zadania spełnia warunki konieczne pierwszego rzędu (warunki Kuhna-Tuckera (5.5)). Znajdziemy teraz wszystkie punkty ,,podejrzane”.
Warunki Kuhna-Tuckera mają następującą postać:
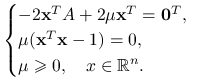 |
Przypadek ![]() . Wówczas
. Wówczas ![]() (z powodu drugiego równania) i pierwsze równanie przyjmuje postać
(z powodu drugiego równania) i pierwsze równanie przyjmuje postać ![]() , którą poprzez transponowanie obu stron sprowadzamy do
, którą poprzez transponowanie obu stron sprowadzamy do
Równanie to spełnione jest przez wszystkie ![]() ,
, ![]() . W szczególności ma ono co najmniej jedno rozwiązanie (
. W szczególności ma ono co najmniej jedno rozwiązanie (![]() ).
).
Przypadek ![]() . Teraz nic nie możemy powiedzieć o
. Teraz nic nie możemy powiedzieć o ![]() . Może być zerowe lub dodatnie. Pierwsze równanie przyjmuje jednak postać
. Może być zerowe lub dodatnie. Pierwsze równanie przyjmuje jednak postać
![]() , które po stransponowaniu wygląda następująco:
, które po stransponowaniu wygląda następująco:
Rozwiązaniami są zatem wektory własne (![]() ) odpowiadające nieujemnym wartościom własnym (
) odpowiadające nieujemnym wartościom własnym (![]() ). Zbiór rozwiązań może być pusty, jeśli wszystkie wartości własne są ujemne.
). Zbiór rozwiązań może być pusty, jeśli wszystkie wartości własne są ujemne.
Podsumowując, zbiór punktów podejrzanych, czyli punktów, w których spełniony jest warunek konieczny pierwszego rzędu, ma postać:
Na obecnym etapie nie mamy żadnej techniki pozwalającej na znalezienie rozwiązania. Możemy tylko posłużyć się zdrowym rozsądkiem. Otóż, jeśli ![]() , to wartość funkcji celu
, to wartość funkcji celu ![]() jest zerowa. Dla dowolnego elementu drugiego zbioru, wartość funkcji celu jest równa wartości własnej. Możemy zatem wyciągnąć następujący wniosek: jeśli maksymalna wartość własna jest dodatnia, to każdy wektor jej odpowiadający jest rozwiązaniem globalnym. Jeśli macierz
jest zerowa. Dla dowolnego elementu drugiego zbioru, wartość funkcji celu jest równa wartości własnej. Możemy zatem wyciągnąć następujący wniosek: jeśli maksymalna wartość własna jest dodatnia, to każdy wektor jej odpowiadający jest rozwiązaniem globalnym. Jeśli macierz ![]() nie ma wartości własnych większych od zera, to rozwiązaniem jest dowolny punkt z jądra
nie ma wartości własnych większych od zera, to rozwiązaniem jest dowolny punkt z jądra ![]() o normie nie większej niż
o normie nie większej niż ![]() .
.
6.3. Zadania
Ćwiczenie 6.1
Uzasadnij prawdziwość stwierdzenia umieszczonego w uwadze 6.1, by później udowodnić, że ![]() , gdzie
, gdzie ![]() zdefiniowane jest w lemacie 6.1.
zdefiniowane jest w lemacie 6.1.
Ćwiczenie 6.2
Przez ”punkty podejrzane” problemu optymalizacyjnego rozumiemy takie punkty dopuszczalne, w których nie są spełnione warunki regularności albo spełnione są warunki konieczne pierwszego rzędu. Znajdź wszystkie punkty podejrzane dla następującego problemu optymalizacyjnego:
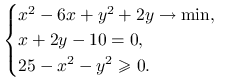 |
Czy w którymś z nich jest rozwiązanie? Jeśli tak, to w którym? Odpowiedź uzasadnij.
Ćwiczenie 6.3
Znajdź zbiór rozwiązań problemu optymalizacyjnego
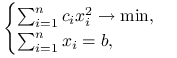 |
gdzie ![]() . Uzasadnij, że są to wszystkie rozwiązania.
. Uzasadnij, że są to wszystkie rozwiązania.
Ćwiczenie 6.4
Znajdź rozwiązania globalne problemu optymalizacyjnego
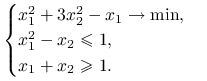 |
Ćwiczenie 6.5
Znajdź minima i maksima globalne funkcji
na zbiorze