12. Wykład XII (kolokwium), 18.XII.2009
- 1. (15p.)
-
Rozważamy rodzinę modeli Blacka
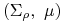 , gdzie
, gdzie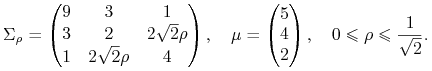
-
 Znaleźć (w podanym przedziale) wszystkie wartości
parametru
Znaleźć (w podanym przedziale) wszystkie wartości
parametru 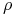 , przy których prosta krytyczna jest równoległa do
prostej boku
, przy których prosta krytyczna jest równoległa do
prostej boku 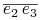 .
. -
 Jaka jest wtedy odległość prostej krytycznej
od prostej boku
Jaka jest wtedy odległość prostej krytycznej
od prostej boku 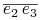 ?
?
-
- 2. (15p.)
-
Wychodzimy od znanego przykładu
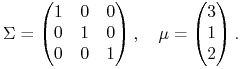
Zwiększamy teraz
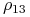 do pierwszej napotkanej wartości, przy
której prosta krytyczna w takim modelu Blacka przechodzi przez
wierzchołek
do pierwszej napotkanej wartości, przy
której prosta krytyczna w takim modelu Blacka przechodzi przez
wierzchołek 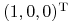 . Znaleźć łamaną wierzchołkową
i łamaną efektywną w uzyskanym modelu Markowitza. Wykonać odpowiednie
rysunki.
. Znaleźć łamaną wierzchołkową
i łamaną efektywną w uzyskanym modelu Markowitza. Wykonać odpowiednie
rysunki. - 3. (10p.)
-
Rozważamy inny znany przykład modelu Markowitza
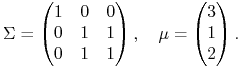
Znaleźć w tym modelu portfel optymalny
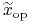 ze względu na stopę bezryzykowną
ze względu na stopę bezryzykowną 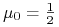 (optymalny,
tzn. maksymalizujący współczynnik Sharpe'a).
(optymalny,
tzn. maksymalizujący współczynnik Sharpe'a).——————————————————————————————————————–
- Pytanie dodatkowe
-
, będące przedłużeniem zadania nr 1 (NIEOBOWIĄZKOWE):
-
 Czy
Czy 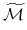 -obraz prostej boku
-obraz prostej boku
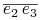 jest wtedy przesunięciem równoległym pocisku
Markowitza oglądanego na płaszczyźnie
jest wtedy przesunięciem równoległym pocisku
Markowitza oglądanego na płaszczyźnie 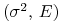 ?
?
Jeśli tak, to o jaki wektor?
Za odpowiedź na to pytanie można uzyskać do 8p., przy czym łączny wynik z kolokwium nie może przekroczyć 40p.
-
Przykładowe rozwiązanie Zadania 1 z kolokwium (patrz też Ćwiczenie 5.1 w Wykładzie V, które mieści też w sobie Pytanie dodatkowe z kolokwium).
Prosta krytyczna ma [więc] równanie
| (12.1) |
gdzie ![]() pozostaje do wyznaczenia. Piszemy to równanie
w postaci wynikającej z Twierdzenia 5.1
w Wykładzie V:
pozostaje do wyznaczenia. Piszemy to równanie
w postaci wynikającej z Twierdzenia 5.1
w Wykładzie V:
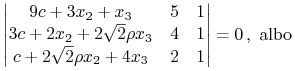 |
| (12.2) |
Warunkiem koniecznym, by równania (12.1) i (12.2)
były tym samym, jest równość współczynników przy ![]() i
i ![]() w (12.2),
w (12.2), ![]() , stąd
, stąd
![]() , jedyne rozwiązanie,
i przy tym leżące w przedziale
, jedyne rozwiązanie,
i przy tym leżące w przedziale ![]() .
.
Wtedy wnioskiem z (12.1) i (12.2) jest
![]() , albo
, albo
![]() . By znaleźć odległość prostej krytycznej
. By znaleźć odległość prostej krytycznej
![]() od prostej boku
od prostej boku ![]() ,
tzn. prostej
,
tzn. prostej ![]() , zauważamy, że przy zmianie wartości
const (w
, zauważamy, że przy zmianie wartości
const (w ![]() ) od 1 do 0, twierdzenie Pitagorasa
mówi, że odpowiednie proste są odległe o
) od 1 do 0, twierdzenie Pitagorasa
mówi, że odpowiednie proste są odległe o ![]() .
Zatem, z proporcjonalności, przy zmianie const od 0 do
.
Zatem, z proporcjonalności, przy zmianie const od 0 do
![]() , odległość odpowiednich prostych wynosi
, odległość odpowiednich prostych wynosi
![]() .
.
Uwaga 12.1
– ostrzeżenie do rozwiązania zadania 1 z kolokwium.
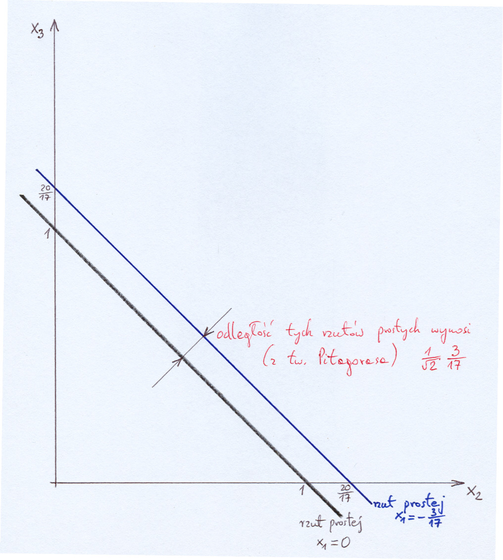
Studenci często szukają tej odległości prostych równoległych
[leżących w położonej ukośnie płaszczyźnie ![]() ]
używając rzutów tych prostych na płaszczyznę
]
używając rzutów tych prostych na płaszczyznę ![]() [uwaga – w wersji pdf rysunek jest na następnej stronie]:
[uwaga – w wersji pdf rysunek jest na następnej stronie]:
Następnie, pracując w tej płaszczyźnie, udzielają różnych odpowiedzi:
![]() ,
, ![]() ,
,
![]() . Ta ostatnia
liczba jest odległością prostych na powyższym rysunku, jednak
żadna z tych liczb nie jest odpowiedzią do pytania
w zadaniu.
. Ta ostatnia
liczba jest odległością prostych na powyższym rysunku, jednak
żadna z tych liczb nie jest odpowiedzią do pytania
w zadaniu.
Odpowiedź liczbowa do Pytania dodatkowego z kolokwium:
obraz prostej krytycznej ![]() (czyli pocisk
Markowitza) oglądany na płaszczyźnie
(czyli pocisk
Markowitza) oglądany na płaszczyźnie ![]() ma równanie
ma równanie
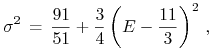 |
(12.3) |
natomiast obraz prostej ![]() ma równanie
ma równanie
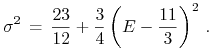 |
(12.4) |
Ten drugi obraz jest więc przesunięciem równoległym pierwszego o wektor
![]() , jak na
rysunku poniżej [w wersji pdf Rysunek 12.2 trafia na następną stronę].
, jak na
rysunku poniżej [w wersji pdf Rysunek 12.2 trafia na następną stronę].
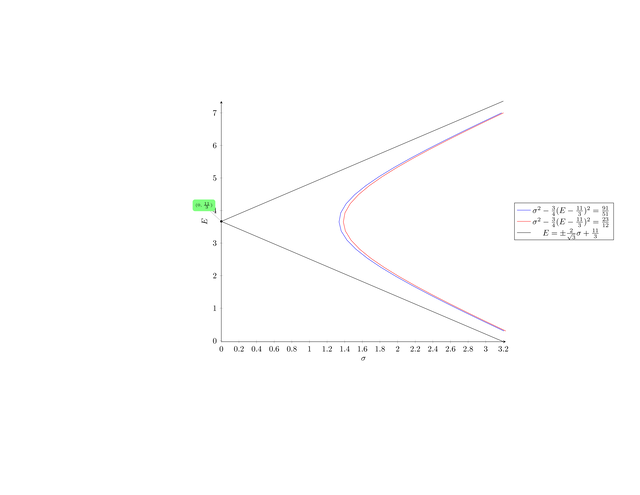
Jeśli chodzi o związane z nimi gałęzie hiperbol,39w zadaniu się
o nie nie pytano to mają one, oczywiście, te same asymptoty
przecinające oś ![]() na wysokości
na wysokości ![]() ,
ze stosunkiem długości półoś
,
ze stosunkiem długości półoś ![]() .
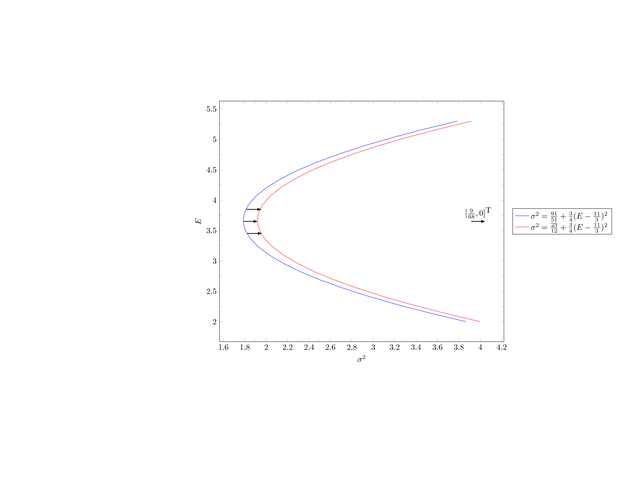
Jednak konkretne wartości długości półoś są różne: dla hiperboli
(12.3) (niebieskiej na Rysunku 12.3 poniżej) wynoszą one
.
Jednak konkretne wartości długości półoś są różne: dla hiperboli
(12.3) (niebieskiej na Rysunku 12.3 poniżej) wynoszą one
![]() ,
, ![]() , zaś dla hiperboli
(12.4) (czerwonej na Rysunku 12.3) wynoszą
, zaś dla hiperboli
(12.4) (czerwonej na Rysunku 12.3) wynoszą
![]() ,
, ![]() . Oto te gałęzie
[w wersji pdf Rysunek 12.3 przeskakuje na następną stronę]:
. Oto te gałęzie
[w wersji pdf Rysunek 12.3 przeskakuje na następną stronę]: