14. Wykład XIV, 15.I.2010

Pod koniec poprzedniego wykładu poznaliśmy klasę funkcji wielu zmiennych, które są pseudo-wklęsłe lub pseudo-wypukłe. Najważniejszą dla nas sprawą związaną z tymi funkcjami jest to, że zachodzi dla nich wersja twierdzenia Karusha-Kuhna-Tuckera! Czasami mówi się krótko, że to twierdzenie, i to w formacie `wteddy', jest też prawdziwe w kategorii pseudo-wypukłej. Podajemy je tutaj, bez dowodu jak i Twierdzenie 9.2, w nienajogólniejszej wersji – tylko przy ograniczeniach nierównościowych (bez równościowych, bo w zastosowaniu nasze funkcje będą niezmiennicze ze względu na skalowanie argumentu). Ponadto warunki nierównościowe są tylko w postaci liniowej. Większej ogólności nie potrzebujemy; byłaby tylko naszym wrogiem, nie zaś sojusznikiem.
(Większą ogólność czytelnik znajdzie już w pionierskiej pracy [18]. To właśnie tam, na stronie 281, zdefiniowane zostały funkcje pseudo-wklęsłe i pseudo-wypukłe, natomiast Theorem 1 na stronach 284-5 jest ogólną wersją twierdzenia typu K-KT w kategorii pseudo-wypukłej i w formacie `wteddy'. Nazwisko Karush nie pojawia się w [18]. Warto też zwrócić uwagę na `Section 3. Remarks on pseudo-convex functions' na stronach 288-9. Lokalne minimum jest zawsze dla tych funkcji globalnym minimum (!) i własność tę dziedziczy nawet pewna jeszcze szersza klasa funkcji ściśle quasi-wypukłych, także zdefiniowana w [18].)

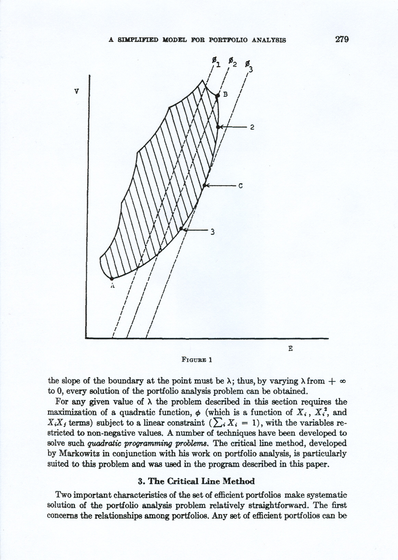
Twierdzenie 14.1 (Karush; Kuhn, Tucker; wersja znacznie późniejsza, w kategorii pseudo-wypukłej)

Niech $G\subset\mathbb{R}^{k}$ będzie otwarty i wypukły, zaś $f\colon G\to\mathbb{R}$ będzie pseudo-wklęsła (pseudo-wypukła) na $G$ . Niech ponadto punkt $x=x_{0}\in G$ spełnia warunki

$\tag{$\intercal\intercal$}a_{i}^{{\text{T}}}x\le b_{i}\,,\qquad i=1,\, 2,\dots,\, l\,,$

(14.1)

gdzie $b_{i}\in\mathbb{R}$ , $a_{i}\in\mathbb{R}^{k}$ . Wtedy $x_{0}$ jest punktem globalnego warunkowego maksimum (minimum) funkcji $f$ przy warunkach (ograniczeniach) (14.1) $\Longleftrightarrow$

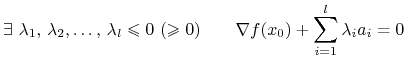$\exists\,\,\lambda _{1},\,\lambda _{2},\dots,\,\lambda _{l}\le 0\ (\ge 0)\qquad\nabla f(x_{0})+\sum _{{i=1}}^{l}\lambda _{i}a_{i}=0$

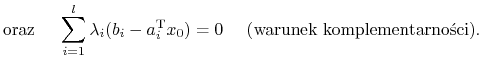$\text{oraz }\quad\sum _{{i=1}}^{l}\lambda _{i}(b_{i}-a_{i}^{{\text{T}}}x_{0})=0\quad\text{ (warunek komplementarności)}.$

Z punktu widzenia formalnego prawie nie ma tu różnic z wersją podaną w Wykładzie IX jako Twierdzenie 9.2. I wtedy i teraz mamy bowiem do czynienia z produktami pochodnymi od fundamentalnych rezultatów zawartych w pracach [11] i [14], o czym była już mowa w Wykładzie IX. Należy jednak pamiętać – powtarzamy to – że Karush oraz Kuhn z Tuckerem dawali tylko warunki konieczne dla ekstremum warunkowego z ograniczeniami nierównościowymi. Dopiero w kategorii wypukłej (Twierdzenie 9.2) bądź pseudo-wypukłej (Twierdzenie 14.1) stają się one warunkami równoważnymi, i to od razu na globalne ekstremum warunkowe.
Teraz do dzieła: wyruszamy na poszukiwanie w analizie portfelowej funkcji pseudo-wklęsłej określonej na dziedzinie wypukłej, i do tego mającej odpowiednie maksimum warunkowe.

Szczegółowa analiza funkcji prowadzącej do współczynnika Sharpe'a

Innym – a przy tym w analizie portfelowej najważniejszym! – przykładem funkcji, która nie jest ani wklęsła, ani wypukła, jest tzw. pre-współczynnik Sharpe'a. Dokładniej, mając dane $\Sigma,\,\mu,\,\mu _{0}$ , gdzie $\Sigma>0$ , $\mu\nparallel e$ (to nasze dawne założenie (5.2)) oraz: $\mu _{0}<E_{0}=\frac{\beta}{\gamma}$ w aspekcie B, względnie $\mu _{0}<\underset{1\le i\le k}{\max}\mu _{i}$ w aspekcie M, rozważamy funkcję

$G\,=\,\{ x\in\mathbb{R}^{k}\,\big|\,(\mu-\mu _{0}e)^{{\text{T}}}x>0\,,\ e^{{\text{T}}}x>0\}\ni x\longmapsto S(x)=\frac{(\mu-\mu _{0}e)^{{\text{T}}}x}{\sqrt{x^{{\text{T}}}\Sigma\, x}}\,,$

(14.2)

określoną na otwartym i wypukłym (co widoczne) zbiorze $G\subset\mathbb{R}^{k}$ .
Zauważamy od razu, że gdy $x\in G$ oraz $e^{{\text{T}}}x=1$ , wtedy $S(x)$ jest po prostu współczynnikiem Sharpe'a, przy stopie bezryzykownej wynoszącej $\mu _{0}$ , portfela $x$ . Jest tak zarówno w aspekcie B, jak i M.

Co prawda – szczegół dość istotny – w żadnym z aspektów nie liczymy tak współczynników Sharpe'a wszystkich dostępnych portfeli, a tylko tych, które mają ten współczynnik dodatni. Idzie jednak o jego maksymalizację i w każdym z aspektów jasno widać, że są portfele o tym współczynniku dodatnim.

Obserwacja. 14.1 Przy wymienionych wyżej założeniach, każda taka funkcja $S$ [którą w analizie portfelowej chcemy maksymalizować] nie jest wklęsła na $G$ .

Uzasadnienie.⁴⁷zadziwiająco niekrótkie, zastępujące inne, nie do końca przekonywujące, podane podczas samych wykładów (w [13] treść Obserwacji 14.1 była zadaniem z gwiazdką) Oznaczając dla krótkości $\nu=\mu-\mu _{0}e$ ( $\nu\ne 0$ , bo (5.2)), mamy zwartą postać wzoru na funkcję $S$ , $S(x)=\nu^{{\text{T}}}x\left(x^{{\text{T}}}\Sigma\, x\right)^{{-\frac{1}{2}}}$ , dzięki czemu szybko liczymy jej gradient:

$\nabla S(x)^{{\text{T}}}\,=\,\nu^{{\text{T}}}x\left(x^{{\text{T}}}\Sigma\, x\right)^{{-\frac{1}{2}}}+\nu^{{\text{T}}}x\left(-\frac{1}{2}\right)\left(x^{{\text{T}}}\Sigma\, x\right)^{{-\frac{3}{2}}}2x^{{\text{T}}}\Sigma\,\,=\,\left(x^{{\text{T}}}\Sigma\, x\right)^{{-\frac{1}{2}}}\left(\nu^{{\text{T}}}-\frac{\nu^{{\text{T}}}x}{x^{{\text{T}}}\Sigma\, x}x^{{\text{T}}}\Sigma\right).$

(14.3)

Pokażemy, że w dziedzinie $G$ niezwykle często zachodzi nierówność pojawiająca się w definicji ścisłej wypukłości funkcji różniczkowalnych,

$S(y)>S(x)+\nabla S(x)^{{\text{T}}}(y-x)\,.$

(14.4)

Szukamy zatem takich ,,złych” par $(x,\, y)\in G\times G$ , że

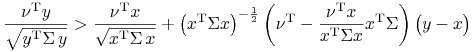$\frac{\nu^{{\text{T}}}y}{\sqrt{y^{{\text{T}}}\Sigma\, y}}>\frac{\nu^{{\text{T}}}x}{\sqrt{x^{{\text{T}}}\Sigma\, x}}+\left(x^{{\text{T}}}\Sigma x\right)^{{-\frac{1}{2}}}\left(\nu^{{\text{T}}}-\frac{\nu^{{\text{T}}}x}{x^{{\text{T}}}\Sigma x}x^{{\text{T}}}\Sigma\right)\big(y-x\big)$

(porównaj (14.3)). Lub, równoważnie,

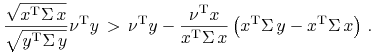$\frac{\sqrt{x^{{\text{T}}}\Sigma\, x}}{\sqrt{y^{{\text{T}}}\Sigma\, y}}\nu^{{\text{T}}}y\,>\,\nu^{{\text{T}}}y-\frac{\nu^{{\text{T}}}x}{x^{{\text{T}}}\Sigma\, x}\left(x^{{\text{T}}}\Sigma\, y-x^{{\text{T}}}\Sigma\, x\right)\,.$

Lub jeszcze równoważnie,

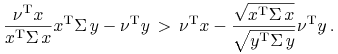$\frac{\nu^{{\text{T}}}x}{x^{{\text{T}}}\Sigma\, x}x^{{\text{T}}}\Sigma\, y-\nu^{{\text{T}}}y\,>\,\nu^{{\text{T}}}x-\frac{\sqrt{x^{{\text{T}}}\Sigma\, x}}{\sqrt{y^{{\text{T}}}\Sigma\, y}}\nu^{{\text{T}}}y\,.$

(14.5)

Jak to spełnić? Okaże się, że da się to uzyskać przy dowolnym wektorze $x\in G$ takim, że $x\nparallel\Sigma^{{-1}}\nu$ , albo, co tutaj równoważne, $\Sigma x\nparallel\nu$ . Ustalmy dowolny taki właśnie wektor $x$ .

Zmieniajmy teraz $y$ , biorąc $ay$ zamiast $y$ , $a>0$ . Wtedy nowa lewa strona w (14.5) to (stara LHS) $\cdot a$ , podczas gdy prawa strona w (14.5) pozostaje niezmienna! Wystarczy więc, by stara LHS była dodatnia. Wtedy (biorąc dostatecznie duże $a>1$ ) już łatwo uzyskamy pożądaną nierówność dla poprawionej pary wektorów $x$ i $ay$ . Jak więc zapewnić sobie $\frac{\nu^{{\text{T}}}x}{x^{{\text{T}}}\Sigma\, x}x^{{\text{T}}}\Sigma\, y-\nu^{{\text{T}}}y>0$ ?

Szukajmy takich wektorów $y$ (jeszcze przed ich ewentualnym przeskalowaniem) w postaci $y=x+h$ . Po podstawieniu i skróceniu wyrazów ma więc być $\frac{\nu^{{\text{T}}}x}{x^{{\text{T}}}\Sigma\, x}x^{{\text{T}}}\Sigma\, h-\nu^{{\text{T}}}h>0$ , albo równoważnie

$h^{{\text{T}}}\left(\frac{\nu^{{\text{T}}}x}{x^{{\text{T}}}\Sigma\, x}\Sigma x-\nu\right)\,>\, 0\,.$

(14.6)

Wektor w nawiasie jest niezerowy – po to właśnie zrobiliśmy założenie $\Sigma x\nparallel\nu$ . Łatwo zatem znaleźć taki wektor $h$ , by zachodziła nierówność (14.6) i przy tym taki, by $x+h\in G$ . (Np, wobec otwartości zbioru $G$ , dobry jest każdy $h$ spełniający (14.6) i dostatecznie mały co do długości; euklidesowej, czy też wyznaczonej przez iloczyn skalarny dawany macierzą $\Sigma$ – bez znaczenia.)

To już koniec (at long last!) uzasadniania Obserwacji 14.1. Nierówność (14.5) zachodzi dla wektorów $x$ oraz $y=a(x+h)$ wyspecyfikowanych w trakcie tego uzasadniania. Reasumując, pasują tu m. in. prawie wszystkie $x\in G$ wraz z dobieranymi do tych $x$ -ów z ogromną swobodą wektorami $y=a(x+h)$ .

Przykład 14.1

Prześledźmy jeszcze etapy powyższego uzasadnienia na konkretnym przykładzie

$k=2,\quad\Sigma=\begin{pmatrix}1&0\\ 0&2\end{pmatrix},\quad\mu=\begin{pmatrix}3\\ 4\end{pmatrix},\ \mu _{0}=1,\ x=\begin{pmatrix}2\\ 0\end{pmatrix}\,,$

$\nu=\begin{pmatrix}2\\ 3\end{pmatrix},\quad\frac{\nu^{{\text{T}}}x}{x^{{\text{T}}}\Sigma\, x}\Sigma x-\nu=\begin{pmatrix}0\\ -3\end{pmatrix}\,.$

Weźmy więc np $h=\begin{pmatrix}0\\ -1\end{pmatrix}$ ; wtedy nierówność (14.6) jest oczywiście spełniona. Czy dla tego $x$ oraz $y=x+h$ od razu spełniona jest nierówność (14.5)?
Otóż nie, bo $3<4-\frac{2}{\sqrt{6}}$ . Lewą stronę trzeba pomocniczo pomnożyć przez dostatecznie dużą liczbę $a>1$ . Tutaj np wystarcza wziąć $a=\frac{11}{10}$ , bo już $3\cdot\frac{11}{10}>4-\frac{2}{\sqrt{6}}$ . Wtedy dla $x$ jw i nowego

$y\,=\,\frac{11}{10}\left(\begin{pmatrix}2\\ 0\end{pmatrix}+\begin{pmatrix}0\\ -1\end{pmatrix}\right)\,=\,\begin{pmatrix}\frac{11}{5}\\ -\frac{11}{10}\end{pmatrix}$

mamy już jak w (14.4). Mianowicie $S(x)=2$ , $\nabla S(x)^{{\text{T}}}=\Big(0,\,\frac{3}{2}\Big)$ , $S(y)=\frac{1}{\sqrt{6}}$ , no i

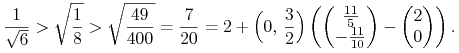$\frac{1}{\sqrt{6}}>\sqrt{\frac{1}{8}}>\sqrt{\frac{49}{400}}=\frac{7}{20}=2+\Big(0,\,\frac{3}{2}\Big)\left(\begin{pmatrix}\frac{11}{5}\\ -\frac{11}{10}\end{pmatrix}-\begin{pmatrix}2\\ 0\end{pmatrix}\right).$

Uwaga 14.1

Przykład 14.1 pokazuje też przy okazji, że pre-współczynnik Sharpe'a nie jest różniczkowalną funkcją wypukłą (choć taka wiadomość jest dla nas zupełnie marginesowa, bo przecież chcemy ten współczynnik maksymalizować, nie zaś minimalizować). Istotnie, przed przeskalowaniem wektora $y$ mieliśmy tam nierówność $S(y)<S(x)+\nabla(x)^{{\text{T}}}(y-x)$ : $\frac{1}{\sqrt{6}}<\frac{1}{2}=2+\big[0,\,\frac{3}{2}\big]\left(\begin{smallmatrix}0\\ -1\end{smallmatrix}\right)$ łamiącą różniczkowalną wypukłość.

Uwaga 14.2

Uzasadnienie Obserwacji 14.1 nie poszło nam szybko, bo chodziło o pewne nierówności charakterystyczne dla ścisłej wypukłości funkcji różniczkowalnych. Takie nierówności są – w sytuacji z Obserwacji 14.1 – sprawą delikatną. Mianowicie, w (14.5) szukane były pary $x,\, y\in G$ takie, że

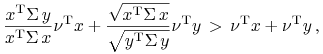$\frac{x^{{\text{T}}}\Sigma\, y}{x^{{\text{T}}}\Sigma\, x}\nu^{{\text{T}}}x+\frac{\sqrt{x^{{\text{T}}}\Sigma\, x}}{\sqrt{y^{{\text{T}}}\Sigma\, y}}\nu^{{\text{T}}}y\,>\,\nu^{{\text{T}}}x+\nu^{{\text{T}}}y\,,$

przy czym oba składniki po prawej stronie były, z definicji zbioru $G$ , dodatnie. Zakładając nawet, że $x^{{\text{T}}}\Sigma\, y>0$ , tzn., że i po lewej stronie oba składniki były dodatnie, mimo wszystko iloczyn tych składników po lewej stronie, czyli liczba

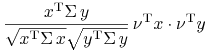$\frac{x^{{\text{T}}}\Sigma\, y}{\sqrt{x^{{\text{T}}}\Sigma\, x}\sqrt{y^{{\text{T}}}\Sigma\, y}}\,\nu^{{\text{T}}}x\cdot\nu^{{\text{T}}}y$

był, z nierówności Schwarza, niewiększy niż iloczyn $\nu^{{\text{T}}}x\cdot\nu^{{\text{T}}}y$ składników po prawej stronie; najczęściej zaś był po prostu mniejszy. Otóż potrzeba pewnej gimnastyki, by przy mniejszym iloczynie dwóch czynników mieć (jednak) większą sumę tych czynników. Taką sytuację udało nam się w sposób ścisły wygenerować.

Natomiast okazuje się, że takie funkcje $S$ są pseudo-wklęsłe.

Twierdzenie 14.2

Przy założeniach jak na początku bieżącego wykładu, pre-współczynnik Sharpe'a $S$ jest funkcją pseudo-wklęsłą na $G$ .

Zakładamy, że $\nabla S(x)^{{\text{T}}}(y-x)\le 0$ , przy czym gradient(y) $\nabla S(x)^{{\text{T}}}$ został(y) już policzony(e) w uzasadnieniu Obserwacji 14.1 powyżej. Zapisujemy to w postaci rozwiniętej

	$\displaystyle 0\ge\left(x^{{\text{T}}}\Sigma\, x\right)^{{-\frac{1}{2}}}$	$\displaystyle\left(\nu^{{\text{T}}}y-\nu^{{\text{T}}}x-\frac{\nu^{{\text{T}}}x}{x^{{\text{T}}}\Sigma\, x}x^{{\text{T}}}\Sigma(y-x)\right)$
	$\displaystyle=$	$\displaystyle\left(x^{{\text{T}}}\Sigma\, x\right)^{{-\frac{1}{2}}}\left(\nu^{{\text{T}}}y-\frac{\nu^{{\text{T}}}x}{x^{{\text{T}}}\Sigma\, x}x^{{\text{T}}}\Sigma\, y\right),$

albo równoważnie – patrz lewa nierówność poniżej, a potem kontynuując dalej (prawa nierówność poniżej) przy pomocy nierówności Schwarza:

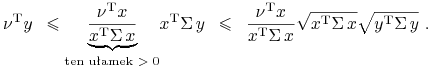$\nu^{{\text{T}}}y\,\,\,\le\underset{\text{ten ułamek $>0$}}{\underbrace{\frac{\nu^{{\text{T}}}x}{x^{{\text{T}}}\Sigma\, x}}}x^{{\text{T}}}\Sigma\, y\,\,\,\le\,\,\,\frac{\nu^{{\text{T}}}x}{x^{{\text{T}}}\Sigma\, x}\sqrt{x^{{\text{T}}}\Sigma\, x}\sqrt{y^{{\text{T}}}\Sigma\, y}\,\,.$

To już daje

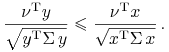$\frac{\nu^{{\text{T}}}y}{\sqrt{y^{{\text{T}}}\Sigma\, y}}\le\frac{\nu^{{\text{T}}}x}{\sqrt{x^{{\text{T}}}\Sigma\, x}}\,.$

∎

Maksymalizacja współczynnika Sharpe'a, w aspekcie M i przy silnych założeniach.

Aspekt M oznacza, że chcemy maksymalizować pre-współczynnik Sharpe'a $S$ na zbiorze $G\cap\{ x\ge 0\}$ . Nie ma więc tu żadnych ograniczeń równościowych (pracujemy z pre-współczynnikiem niezmienniczym ze względu na skalowania), zaś ograniczenia nierównościowe to właśnie $x\ge 0$ (jedna nierówność wektorowa skrywająca $k$ nierówności skalarnych). W tej części zakładamy, że $\Sigma>0$ . Zaraz puścimy w ruch budowaną od dawna maszynerię.

Jest niezmiernie ważne, że punkty maksymalizujące funkcję $S$ na $G$ przy podanych ograniczeniach w ogóle istnieją – że mamy czego szukać przy pomocy Twierdzeń 14.1 i 14.2.
Istotnie, z racji dodatniej jednorodności stopnia 0 funkcji $S$ można rozważać tylko argumenty z $G\cap\Delta^{k}$ , zaś skoro o maksymalizację $S$ chodzi, to ,,nic złego nam nie dojdzie” gdy będziemy rozważać wszystkie portfele z $\Delta^{k}$ (bo wobec założeń o $\mu _{0}$ istnieją portfele $x\in\Delta^{k}$ , dla których $S(x)>0$ , więc maksymalizacja $S$ i tak odbywać się będzie w części $G\,\cap\,\Delta^{k}$ ). Dalej to już standard z pogranicza analizy i topologii: ciągłość $S$ na zwartym zbiorze $\Delta^{k}$ i twierdzenie Weierstrassa.
Tak więc maksimum funkcji $S$ na $G\,\cap\,\{ x\ge 0\}$ jest osiągane. Przechodzimy teraz do wyłuskiwania tych miejsc, gdzie to się dzieje. Będzie ich dużo, bo przecież wspomniana dodatnia jednorodność stopnia 0.

W Twierdzeniu 14.1 przyjmujemy $l=k$ oraz $a_{i}=-e_{i}$ , $b_{i}=0$ dla $i=1,\, 2,\dots,\, k$ . Wtedy warunki (14.1) właśnie kodują nieujemność wszystkich składowych wektora $x$ . (Spotykaliśmy się już z takim kodowaniem nieujemności składowych portfela Markowitza przy stosowaniu Twierdzenia 9.2. Można powiedzieć, że jest to dla nas chleb powszedni.)

Na mocy Twierdzenia 14.1, $x_{0}\in G\cap\{ x\ge 0\}$ jest punktem (pre-portfelem) maksymalizującym $S$ na $G\cap\{ x\ge 0\}$ wtedy i tylko wtedy, gdy istnieją niedodatnie współczynniki $\lambda _{1},\dots,\,\lambda _{k}$ takie, że

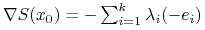$\nabla S(x_{0})=-\sum _{{i=1}}^{k}\lambda _{i}(-e_{i})$ oraz
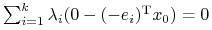$\sum _{{i=1}}^{k}\lambda _{i}(0-(-e_{i})^{{\text{T}}}x_{0})=0$ (z warunku komplementarności).

Pierwszy z tych wzorów pokazuje, że gradient $S$ w $x_{0}$ jest niedodatni jako wektor i równocześnie mówi, że współczynniki $\lambda _{i}$ są po prostu składowymi tego wektora gradientu. To pozwala dużo bardziej operatywnie zapisać drugi wzór, i łącznie w ten sposób

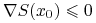$\bullet$ $\nabla S(x_{0})\le 0$ oraz
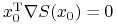$\bullet\bullet$ $x_{0}^{{\text{T}}}\nabla S(x_{0})=0$ .

Teraz należy rozszyfrować $\bullet$ pamiętając, że $\nabla S(x_{0})=\left(x_{0}^{{\text{T}}}\Sigma\, x_{0}\right)^{{-\frac{1}{2}}}\left(\nu-\frac{\nu^{{\text{T}}}x_{0}}{x_{0}^{{\text{T}}}\Sigma\, x_{0}}\Sigma\, x_{0}\right)$ . Pisząc jako
$y_{0}=\frac{\nu^{{\text{T}}}x_{0}}{x_{0}^{{\text{T}}}\Sigma\, x_{0}}x_{0}$ pewną dodatnią wielokrotność portfela $x_{0}$ , $\bullet$ oznacza

$\Sigma y_{0}-\mu+\mu _{0}e\ge 0\,,$

zaś $\bullet\bullet$ oznacza $x_{0}^{{\text{T}}}\big(\Sigma y_{0}-\mu+\mu _{0}e\big)=0$ , albo równoważnie

$y_{0}^{{\text{T}}}\big(\Sigma y_{0}-\mu+\mu _{0}e\big)=0\,,$

przy czym oczywiście $y_{0}\ge 0$ , $e^{{\text{T}}}y_{0}>0$ . To właśnie są nasze stare dobrze znajome związki (11.10).

Uzasadnienie sposobu szukania portfeli optymalnych $\widetilde{x}_{{\text{op}}}$ w teorii Tobina przy $\Sigma>0$ jest teraz zakończone. (W końcówce trochę szybko to poszło; czytelnik nie takiej końcówki się spodziewał po długim wstępie.) Jednak – uwaga – dalece nie jest zakończone przy ogólniejszych macierzach $\Sigma\ge 0$ . Tym przypadkiem zajmiemy się niebawem.

W tym momencie narzuca się, tak: wręcz narzuca się pytanie, czy rozwinięta tu powyżej technika pracy z pre-współczynnikiem Sharpe'a $S$ nie wyprodukowałaby jeszcze raz (niejako po drodze) wzoru na portfele optymalne $x_{{\text{op}}}$ w zmodyfikowanej teorii Tobina, tj przy z powrotem dopuszczanej nieograniczonej krótkiej sprzedaży i, oczywiście, dla $\Sigma>0$ .

Odpowiedź jest twierdząca, bo przecież zerowanie się gradientu funkcji pseudo-wklęsłej w punkcie zbioru otwartego wypukłego jest równoważne jej maksymalizacji na tym zbiorze w tym właśnie punkcie: konieczność tego warunku to fakt ogólny z AM II, sięgający wstecz aż do Fermata (połowa XVII wieku), natomiast jego dostateczność wynika z samej definicji – patrz Definicja 13.1 w Wykładzie XIII.
Mając zatem jakiś $y\in G$ taki, że

$0=\nabla S(y)=\left(y^{{\text{T}}}\Sigma\, y\right)^{{-\frac{1}{2}}}\left(\nu-\frac{\nu^{{\text{T}}}y}{y^{{\text{T}}}\Sigma\, y}\Sigma\, y\right),$

zapisujemy ten fakt w postaci

$\left(\frac{\nu^{{\text{T}}}y}{y^{{\text{T}}}\Sigma\, y}\right)y\,=\,\Sigma^{{-1}}\nu\,.$

(14.7)

Skoro ten $y$ spełnia (14.7), to wszystkie $ty\colon ty\in G$ też spełniają (14.7). Zatem wszystkie $y=t\Sigma^{{-1}}\nu$ , $t>0$ , spełniają (14.7), a wśród nich ten dla $t=\left(e^{{\text{T}}}\Sigma^{{-1}}\nu\right)^{{-1}}$ , tzn. portfel $x_{{\text{op}}}$ . Rozumiemy to tak, że wiele punktów w $G$ maksymalizuje $S$ , lecz wśród nich jest tylko jeden portfel — właśnie portfel $x_{{\text{op}}}$ .

Maksymalizacja współczynnika Sharpe'a, w aspekcie M i teraz przy słabszych założeniach.

Założenie (5.2) jest nie do podważenia – nie mogą wszystkie wartości oczekiwane stóp zwrotu z walorów giełdowych być takie same; mapa Markowitza musi być dwuwymiarowa! Za to do rozważenia jest osłabienie założenia $\Sigma>0$ . W tej części Wykładu XIV zakładamy tylko, że $\Sigma\ge 0$ . Jaką wtedy mamy wiedzę nt portfeli optymalnych?

Jeśli chodzi o aspekt B, to takie osłabienie wiedzy nt macierzy kowariancji, nawet bez zerowania się ryzyka niektórych portfeli, może prowadzić do nieistnienia portfeli optymalnych ze względu na jakąkolwiek ustaloną stopę bezryzykowną. Pamiętamy jeszcze Przykład 7.1 w Wykładzie VII, gdzie po przejściu od aspektu M do aspektu B portfele efektywne po prostu wyparowały. Tymczasem portfel optymalny względem jakiejś stopy $\mu _{0}$ musiałby być efektywny; optymalnych więc nie ma. Zresztą granica minimalna jest pionową prostą $\sigma=\frac{1}{\sqrt{2}}$ jak na Rysunku 7.1, i współczynnik Sharpe'a każdego portfela krytycznego łatwo jest (graficznie) powiększyć.

Dużo ciekawszy jest aspekt M, kiedy to większość dotychczasowych rozważań przechodzi, co prawda tylko dla odpowiednio wybranych wartości $\mu _{0}$ .
Po pierwsze, przy macierzy kowariancji nieujemnie określonej ryzyko portfeli Markowitza nie musi schodzić do zera; widzieliśmy to już w ćwiczeniu w Uwadze 7.2. Wtedy dodatkowe ograniczenie dolne na $\mu _{0}$ zaproponowane w (14.8) poniżej jest puste. Często jednak ryzyko schodzi do zera (choćby w modelach doskonale $\pm$ skorelowanych), i wtedy w mianowniku wyrażenia definiującego współczynnik Sharpe'a może (czy: mogłaby) dziać się katastrofa. By jej uniknąć,⁴⁸by, jak mówią anglosasi, be on the safe side zakładamy w dalszym ciągu, że

$\max\{ E(x)\,\big|\, x\in\Delta^{k}\,,\ \sigma(x)=0\}\,<\,\mu _{0}\,<\,\underset{1\le i\le k}{\max}\mu _{i}$

(14.8)

(piszemy $\max$ zamiast $\sup$ , bo znowu w grę wchodzi ciągła funkcja $E(\cdot)$ na zbiorze zwartym).

Uwaga. Jeśli w $\Delta^{k}$ nie ma portfeli o zerowym ryzyku, to dodatkowego dolnego ograniczenia na $\mu _{0}$ po prostu nie ma.

Pre-współczynnik Sharpe'a $S$ zdefiniujemy teraz nie na całym zbiorze $G$ zdefiniowanym w (14.2), tylko na o wiele mniejszym zbiorze [też, jak i $G$ ] wypukłym i otwartym $\widetilde{G}$ w $\mathbb{R}^{k}$ , $\widetilde{G}\subset G$ . W dobrym określeniu tej dziedziny dla $S$ tkwi teraz główna trudność. Szczególnie chodzi tu o wypukłość zbioru – funkcje pseudo-wklęsłe potrzebują wszak wypukłej dziedziny!
Uwaga. W ważnym fragmencie wykładu przedstawionym tu niżej mignie też przez chwilę jedna najprostsza możliwość, gdy nowy $\widetilde{G}$ będzie starym $G$ . Nie o to nam jednak głównie chodzi …

Konstrukcja dziedziny pre-współczynnika Sharpe'a gdy $\Sigma\ge 0$ .

Zauważamy, że zbiór $Z_{1}=\{ x\in\Delta^{k}\,\big|\,\,\nu^{{\text{T}}}x>0\}$ jest niepusty wypukły (co oczywiste) oraz nie zawiera portfeli o zerowym ryzyku, bo na nich (jeśli takowe w $\Delta^{k}$ są) funkcjonał $\nu^{{\text{T}}}$ jest ujemny – patrz (14.8).

Dla potrzeb dalszego rozumowania, niech $Zero=\{ x\in H\,\big|\ \sigma(x)=0\}$ . Ten zbiór stanowi przeszkodę, choć wyjątkowo może nawet być pusty przy macierzy $\Sigma\ge 0$ (znamy dobrze jeden taki przykład).
Jeśli zbiory $\Delta^{k}$ i $Zero$ są rozłączne, to liczby $\delta$ tu poniżej nie definiujemy. Natomiast jeśli mają one niepuste przecięcie, to zauważamy, że wartości funkcji liniowej $E(\cdot)$ na zbiorach $Z_{1}$ oraz $Zero\,\cap\Delta^{k}$ różnią się – patrz (14.8) – o pewną dodatnią wielkość. Te dwa zbiory wartości są od siebie oddzielone na osi liczbowej, natomiast funkcja $E\colon H\to\mathbb{R}$ jest jednostajnie ciągła. Zatem i zbiory argumentów muszą być oddzielone w przestrzeni $H$ :

$\text{dist}\big(Z_{1},\,\, Zero\cap\Delta^{k}\big)=\delta>0\,.$

(14.9)

Trochę większy kłopot jest z częścią zbioru $Zero$ położoną poza $\Delta^{k}$ — znowu: jeśli tylko jest ona niepusta. (Jeśli jest pusta, to z kolei nie definiujemy liczby $\delta^{{\prime}}$ poniżej.)

Mamy więc sytuację $Zero\setminus\Delta^{k}\ne\emptyset$ .
Przypuśćmy wówczas, że $\text{dist}\big(Z_{1},\,\, Zero\setminus\Delta^{k}\big)=0$ .

Istnieją zatem ciągi portfeli $(x_{n})\subset Z_{1}\subset\Delta^{k}$ oraz $(y_{n})\subset Zero\setminus\Delta^{k}$ takie, że $||x_{n}-y_{n}||\to 0$ gdy $n\to\infty$ . Sympleks $\Delta^{k}$ jest zwarty, więc istnieje podciąg portfeli $\big(x_{{n_{m}}}\big)$ zbieżny do jakiegoś portfela $\overline{x}\in\Delta^{k}$ gdy $m\to\infty$ . Oczywiście też $||y_{{n_{m}}}-\,\overline{x}||\to 0$ gdy $m\to\infty$ .
Wobec $\sigma\big(y_{{n_{m}}}\big)=0$ dla $m\in\mathbb{N}$ , i z ciągłości funkcji $\sigma(\cdot)$ na $H$ , mamy $\sigma(\overline{x})=0$ . W sytuacji, gdy $Zero\,\cap\Delta^{k}=\emptyset$ (tj gdy nie ma liczby $\delta$ ), sprzeczność jest już, bo jednak $\overline{x}\in Zero\cap\Delta^{k}$ .

Jeśli zaś $Zero\cap\Delta^{k}\ne\emptyset$ (liczba $\delta$ jest), wtedy sprzeczność jeszcze przez chwilkę dokuwamy: $\nu^{{\text{T}}}\overline{x}\ge 0$ , bo $\nu^{{\text{T}}}x_{{n_{m}}}>0$ dla $m\in\mathbb{N}$ . Ta własność hipotetycznego portfela Markowitza $\overline{x}$ wraz z wcześniejszą wiadomością $\sigma(\overline{x})=0$ już dają sprzeczność z lewą nierównością w (14.8).
Tak, czy inaczej, portfel $\overline{x}$ nie może istnieć. Tym samym udowodniliśmy ad absurdum, że

$\text{dist}\big(Z_{1},\,\, Zero\setminus\Delta^{k}\big)=\delta^{{\prime}}>0\,,$

(14.10)

o ile tylko $Zero\setminus\Delta^{k}\ne\emptyset$ .

Mamy więc dwie warunkowo zdefiniowane liczby: $\delta$ i $\delta^{{\prime}}$ . Warunkowość oznacza tu, że być może któraś z nich jest nieokreślona, względnie nawet obie są nieokreślone (powtarzamy, że może tak być nawet przy częściowo zdegenerowanej macierzy $\Sigma$ ).

Jeśli obie te liczby są nieokreślone, albo innymi słowy $Zero=\emptyset$ , wtedy … nie dzieje się nic nowego pod słońcem⁴⁹zasada brzytwy Ockhama i kładziemy $\widetilde{G}=G$ . O tej rozczarowującej możliwości wspominaliśmy już w Uwadze wyżej.

Jeśli zaś przynajmniej jedna z tych liczb jest określona, to wnioskiem z (14.9) i/lub (14.10) jest

$\text{dist}\big(Z_{1},\,\, Zero\big)=\min(\delta,\,\delta^{{\prime}})=r>0\,,$

(14.11)

z naturalnym rozumieniem i rolą liczby $r$ gdy jednej z liczb delta nie ma. Teraz już możemy skonstruować zbiór $Z_{2}$ , $H\supset Z_{2}\supset Z_{1}$ , otwarty w $H$ , wypukły i rozłączny z niebezpiecznym zbiorem $Zero$ :

$Z_{2}\,\,=\underset{x\in Z_{1}}{\bigcup}B(x,\, r)\,,$

(14.12)

gdzie $B(x,\, r)$ to kula otwarta w hiperpłaszczyźnie $H$ o środku w $x$ i promieniu $r$ (zawsze w użyciu jest odległość euklidesowa, dziedziczona w $H$ z $\mathbb{R}^{k}$ ).

Otwartość $Z_{2}$ w $H$ jest jasna, rozłączność ze zbiorem $Zero$ wynika z (14.11) (kule w (14.12) są, przypominamy, otwarte). Wypukłość $Z_{2}$ wynika wprost z wypukłości $Z_{1}$ . Dokładniej, pożyteczne jest samodzielnie rozwiązać następujące ogólne

Ćwiczenie 14.1

W przestrzeni euklidesowej $V$ dany jest niepusty zbiór wypukły $Z$ , zaś $r>0$ jest ustaloną liczbą dodatnią. Uzasadnić, że zbiór $\underset{x\in Z}{\bigcup}B(x,\, r)\supset Z$ też jest wypukły w $V$ .

Wybór $Z_{2}$ dokonany w (14.12) jest kluczowy. To pewna wypukła otoczka w $H$ pewnej części sympleksu standardowego $\Delta^{k}$ . Może to jednak być bardzo cienka otoczka w $H$ ( $r$ może być maleńkie dodatnie), niewiele większa od samej otaczanej części sympleksu.

Niech teraz $\widetilde{G}$ będzie po prostu stożkiem nad $Z_{2}$ ,

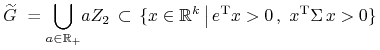$\widetilde{G}\,\,=\underset{a\in\mathbb{R}_{{+}}}{\bigcup}aZ_{2}\,\subset\,\{ x\in\mathbb{R}^{k}\,\big|\, e^{{\text{T}}}x>0\,,\ x^{{\text{T}}}\Sigma\, x>0\}$

(14.13)

(prawa inkluzja jest oczywista). Skoro zbiór $Z_{2}$ był wypukły i otwarty w $H$ , więc zbiór $\widetilde{G}$ zdefiniowany w (14.13) jest z kolei wypukły i otwarty w $\mathbb{R}^{k}$ . Właśnie na takiej dziedzinie $\widetilde{G}$ rozważamy teraz pre-współczynnik Sharpe'a $S\colon\widetilde{G}\ni x\mapsto S(x)$ . Dosyć ciężka walka została stoczona, by był on dobrze określony na całym otwartym i wypukłym $\widetilde{G}$ (pamiętna rozłączność $Z_{2}$ z $Zero$ na poziomie hiperpłaszczyzny $H$ ).

Czy jest to właściwy punkt wyjścia do jego maksymalizacji na całym sympleksie standardowym, oczywiście z wyłączeniem portfeli mających zerowe ryzyko?⁵⁰Taka propozycja dziedziny dla $S$ jest lekko niestandardowa. Ta dziedzina nie obejmuje przecież całego $\Delta^{k}$ bez portfeli zerowego ryzyka! Tak jest, lecz tak też było w łatwiejszej sytuacji $\Sigma>0$ na początku tego wykładu; nie będzie to przeszkadzać w naszej maksymalizacji $S$ . To tylko cena (niejedyna, też założenie (14.8)), jaką musimy zapłacić, by mieć wypukłość dziedziny dla $S$ . Wyjaśnijmy to tutaj dokładniej. Lewą nierówność w (14.8) można przepisać w postaci

$\max\{\nu^{{\text{T}}}x\,\big|\, x\in\Delta^{k}\,,\ \sigma(x)=0\}\,<\, 0\,.$

Skoro jest tak, to także

$\sup\{\nu^{{\text{T}}}x\,\big|\, x\in\Delta^{k}\,,\ \sigma(x)<\sigma _{0}\}\,<\, 0$

dla pewnego dostatecznie małego dodatniego $\sigma _{0}$ . Wobec tego maksymalizacja współczynnika Sharpe'a na zbiorze $\{ x\in\Delta^{k}\,\big|\ \sigma(x)>0\}$ jest tym samym, co jego maksymalizacja na zbiorze $\{ x\in\Delta^{k}\,\big|\ \sigma(x)\ge\sigma _{0}\}$ – bo odpadają tylko pewne ujemne wartości funkcji, która przyjmuje też⁵¹zresztą dokładnie na zbiorze $Z_{1}$ zdefiniowanym wcześniej wartości dodatnie. Na ostatnim zapisanym tu zbiorze ten współczynnik jest funkcją ciągłą, zaś sam zbiór jest zwarty. Przeto jego kres górny na tym zbiorze jest skończony i jest osiągany. To właśnie było nam potrzebne, bo tym samym kres górny współczynnika Sharpe'a na $\{ x\in\Delta^{k}\,\big|\ \sigma(x)>0\}$ jest skończony i osiągany! Przy tym, rzecz prosta, jest on osiągany w punkcie, lub punktach, zbioru $Z_{1}$ , który posłużył nam wcześniej do zaproponowania okrojonej dziedziny dla pre-współczynnika $S$ .
Idziemy teraz za ciosem, bez straty ogólności pozostajemy w naszej dziedzinie dla $S$ i z dodatniej jednorodności stopnia 0 funkcji $S$ dostajemy, że

$\ast$ kres górny $S$ na $\widetilde{G}\cap\{ x\ge 0\}$ jest skończony i jest osiągany.

Twierdzenie 14.3

Gdy $\Sigma\ge 0$ , wtedy warunki (11.10) skrywają wszystkie portfele optymalne w aspekcie M ze względu na stopę bezryzykowną $\mu _{0}$ spełniającą (14.8).
Innymi słowy, również wtedy portfele optymalne (już niekoniecznie jeden jedyny portfel optymalny!) znajduje się, rozwiązując liniowe zagadnienie komplementarności (11.10).

Czytelnik domyśla się już, że kluczowy dla dowodu jest właśnie fakt $\ast$ , czyli osiąganie największej wartości przez $S$ na wymienionym tam zbiorze. Gdyż poza tym cały (gruby, otwarty) $\widetilde{G}$ jest zbiorem wypukłym, na którym funkcja $S$ jest pseudo-wklęsła. Tak samo, jak przy $\Sigma>0$ ten sam pre-współczynnik Sharpe'a był pseudo-wklęsły na (o wiele większym) zbiorze $G\supset\widetilde{G}$ . (Czasami $G$ nie jest ,,o wiele większy”, tylko jest tym samym, co $\widetilde{G}$ , lecz to zupełny szczegół. W trudniejszych sytuacjach $G$ może być o wiele większy niż $\widetilde{G}$ .)
Dowód pseudo-wklęsłości przechodzi bez zmian, bo skurczona dziedzina jest wypukła, wzór na gradient $\nabla S$ pozostaje w mocy, zaś nieostra nierówność Schwarza zachodzi też dla formy dwuliniowej z nieujemnie określoną macierzą współczynników.
Dalej zaś włącza się znowu do akcji Twierdzenie 14.1, drugi raz tak samo prowadząc do warunków (11.10), w 100 $\%$ wiernie charakteryzujących punkty warunkowego maksimum $S$ przy warunkach nieujemności współrzędnych.

∎

Uwaga 14.3 (po dowodzie)

(i) W sytuacji łatwiejszej (początek tego wykładu) wycinaliśmy z $\Delta^{k}$ część $\{\nu^{{\text{T}}}x\le 0\}$ , a potem resztę powiększaliśmy do stożka $G$ (nad tą resztą budowaliśmy stożek $G$ ).
Teraz w trudniejszej sytuacji też wycinamy tę część, lecz dodatkowo musimy też wyciąć zbiór [nieprzyjemny, algebraiczny, niby ,,tylko” stopnia 2, lecz przecież w wielu wymiarach!] $Zero$ . To wycięcie sprawia pewien kłopot, jeśli chodzi o otwartą wypukłość tego, co zostaje. Potem już tylko powiększamy do stożka $\widetilde{G}$ .
Po drodze ubezpieczamy się, postulując w (14.8), by $Zero\,\cap\Delta^{k}\subset\{\nu^{{\text{T}}}x\le\text{pewna liczba ujemna}\}$ . To ubezpieczenie jest absolutnie naturalne – wystarczy je sobie zinterpretować graficznie na pionowej osi na płaszczyźnie $\mathbb{R}^{2}(\sigma,\, E)$ .
Zauważmy jeszcze, by postawić małą kropkę nad ,,i”, że w definicji zbioru $G$ w (14.2) występował warunek $\nu^{{\text{T}}}x>0$ . Natomiast w definicji (14.13) zbioru $\widetilde{G}$ ten warunek eksplicite się nie pojawia i wręcz miejscami może nie być spełniony w $\widetilde{G}$ .
Był on w definicji zbioru $Z_{1}$ i był tam ważny, natomiast mógł się zagubić przy rozszerzaniu $Z_{1}$ do $Z_{2}$ [stożkiem nad którym jest $\widetilde{G}$ ]. Dla samej maksymalizacji funkcji $S$ nie ma to żadnego znaczenia, bo technika K-KT wyłuskuje nam tutaj pre-portfele maksymalizujące $S$ siedzące w $\widetilde{G}\cap\{ x\ge 0\}$ , czyli w stożku nad $Z_{1}$ , gdzie z powrotem (czy: od początku) warunek $\nu^{{\text{T}}}x>0$ zachodzi.

(ii) Twierdzenie 14.3 może zostać/zostanie w pełni ocenione dopiero podczas wykładów APRK2, gdy staje/stanie się czymś nieodzownym w badaniu ważnego modelu Alexandera ogłoszonego w roku 1993 w pracy [2], proponującego dość realistyczne podejście do krótkiej sprzedaży. Nie tak krańcowo restryktywne, jak u Lintnera (porównaj Wykład IX), i też nie tak krańcowo swobodne/nierealistyczne, jak u Blacka i współautorów (porównaj Wykłady V i VI).
W modelu Alexandera macierze kowariancji tylko nieujemnie określone są czymś najbardziej naturalnym pod słońcem.

Gdy to Twierdzenie 14.3 jest już udowodnione, najwyższa pora na ilustrację, jak konkretnie tamte słynne warunki (11.10) pracują w sytuacji, gdy macierz kowariancji jest tylko nieujemnie określona.
W ćwiczeniu poniżej ograniczenie dolne na $\mu _{0}$ w (14.8) jest puste, bo $Zero\cap\Delta^{3}=\emptyset$ . I nawet ,,gorzej”: po prostu $Zero=\emptyset$ , więc w całej konstrukcji dziedziny dla $S$ powyżej można było wziąć $\widetilde{G}=G$ itd. Tym niemniej macierz $\Sigma$ jest tam tylko nieujemnie określona …

Algorytm z Wykładu XI nie działa w sensie dosłownym – nie możemy wszak odwracać macierzy $\Sigma$ . Mimo to, zgodnie z Twierdzeniem 14.3, warunki (11.10) jednak dobrze kodują portfele optymalne w aspekcie M. Rozwiążemy te warunki (lecz dopiero w … Rozwiązaniu ćwiczenia!) ,,całościowo”, czyli łącznie i z marszu rozwiążemy odpowiednie liniowe zagadnienie komplementarności. Do dzieła zatem.

Ćwiczenie 14.2

W słynnym już modelu Markowitza z ćwiczenia w Uwadze 7.2 (Wykład VII) znaleźć portfele optymalne ze względu na bankową stopę bezryzykowną $\mu _{0}\in[0,\, 1]$ . (Podkreślamy, że tym razem chodzi o aspekt M, bo aspektowi B w tym modelu zostało już poświęcone Ćwiczenie 9.2 w Wykładzie IX.)

Rozwiązanie:

Wiemy już z Uwagi 7.2, że w tym modelu wszystkie portfele Markowitza są portfelami relatywnie minimalnego ryzyka. Przy każdej ustalonej wartości $E\in[1,\, 3]$ jest cały odcinek takich portfeli; dla skrajnych wartości $E$ odcinek degeneruje się do punktu – jednego portfela. Więc dla wartości $\overline{E}$ odpowiadającej ustalonej na pionowej osi wartości $\mu _{0}$ powinniśmy mieć cały taki odcinek portfeli optymalnych względem tej stopy bezryzykownej.
Dokładniej, jaką pionową współrzędną $\overline{E}$ ma punkt na górnym ,,wąsie” pocisku $\sigma^{2}-(E-2)^{2}=1$ , $\sigma>0$ (wzór uzyskany w Uwadze 7.2), w którym styczna do pocisku przecina oś $\overrightarrow{OE}$ na wysokości $\mu _{0}<2$ ?
Jest to standardowa geometria analityczna krzywych stożkowych, kiedyś obecna w podręcznikach licealnych: $\overline{E}=\frac{5-2\mu _{0}}{2-\mu _{0}}$ . Konkretnie, gdy $\mu _{0}\in[0,\, 1]$ , wtedy $\overline{E}\in\left[\frac{5}{2},\, 3\right]$ .

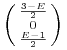Jakie portfele Markowitza przechodzą w mapie Markowitza na punkt pocisku Markowitza położony na wysokości $E$ ?⁵²jedno nazwisko występuje trzy razy w jednym pytaniu, i wszystko jest najzupełniej legalne Na boku $\overline{e_{1}\, e_{3}}$ jest to portfel $\left(\begin{smallmatrix}\frac{3-E}{2}\\ 0\\ \frac{E-1}{2}\end{smallmatrix}\right)$ , natomiast na boku $\overline{e_{2}\, e_{3}}$ — portfel $\left(\begin{smallmatrix}0\\ 3-E\\ E-2\end{smallmatrix}\right)$ . Zatem cały odcinek między tymi skrajnymi portfelami,

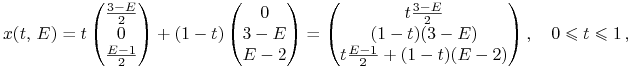$x(t,\, E)=t\begin{pmatrix}\frac{3-E}{2}\\ 0\\ \frac{E-1}{2}\end{pmatrix}+(1-t)\begin{pmatrix}0\\ 3-E\\ E-2\end{pmatrix}=\begin{pmatrix}t\frac{3-E}{2}\\ (1-t)(3-E)\\ t\frac{E-1}{2}+(1-t)(E-2)\end{pmatrix},\quad 0\le t\le 1\,,$

przechodzi na punkt pocisku położony na wysokości $E$ . Gdy podstawimy $E=\frac{5-2\mu _{0}}{2-\mu _{0}}$ i policzymy $\Sigma\, x(t,\, E)$ , wtedy zależność od $t$ znika: $\Sigma\, x(t,\, E)=\frac{1}{2-\mu _{0}}\left(\begin{smallmatrix}1-\mu _{0}\\ 2-\mu _{0}\\ 3-\mu _{0}\end{smallmatrix}\right)$ . Teraz staje się jasne, jak realizuje się krytyczność, o której mowa we wskazówce do Uwagi 7.2:

$\Sigma\, x(t,\, E)=\frac{1}{2-\mu _{0}}\mu-\frac{\mu _{0}}{2-\mu _{0}}e\,.$

Natomiast w terminach problemu (11.10) trzeba oczywiście wziąć $y=y(t,\, E)=(2-\mu _{0})x(t,\, E)$ , który dla rozważanych tu wartości $t$ i $E$ ma wszystkie składowe nieujemne, no i mieć wtedy, właśnie całościowo i niezależnie od oddzielnych etapów, $\Sigma\, y(t,\, E)-\mu+\mu _{0}e=0$ .

Normalizacja pre-portfela $y(t,\, E)$ daje portfel $x(t,\, E)$ optymalny ze względu na stopę $\mu _{0}$ . Zależność tych portfeli od $t$ jest oczywiście afiniczna. Jest ich wiele przy ustalonej $\mu _{0}$ , nie ma mowy o jakiejkolwiek jednoznaczności portfela optymalnego (od dawna wiemy, że cały przykład jest co najmniej dziwny). Natomiast jak te portfele zależą od $\mu _{0}$ ?
To też nic trudnego. Do znanego już wzoru na $x(t,\, E)$ podstawiamy znalezioną zależność $E=E(\mu _{0})$ , dostając

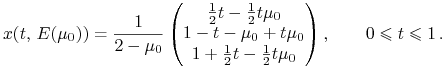$x(t,\, E(\mu _{0}))=\frac{1}{2-\mu _{0}}\begin{pmatrix}\frac{1}{2}t-\frac{1}{2}t\mu _{0}\\ 1-t-\mu _{0}+t\mu _{0}\\ 1+\frac{1}{2}t-\frac{1}{2}t\mu _{0}\end{pmatrix},\qquad 0\le t\le 1\,.$

Ćwiczenie 14.3 (kontynuacja Ćwiczenia 14.2)

Znaleźć najmniejszą wartość stopy bezryzykownej $\mu _{0}$ , ze względu na którą portfel $e_{3}$ jest optymalny w modelu Markowitza z Ćwiczenia 14.2.

Wskazać jakąś inną większą stopę bezryzykowną, ze względu na którą portfel $e_{3}$ także jest optymalny w aspekcie M.
Czy jest to jedyny portfel optymalny w aspekcie M przy tej większej stopie bezryzykownej?

Na koniec tych rozważań o portfelach optymalnych ze względu na stopę(y) $\mu _{0}$ w aspekcie M, przeprowadźmy jedną dłuższą analizę ich zachowania i zmienności w trochę podkręconym przykładzie Krzyżewskiego. Mianowicie, przy niezmienionej tamtej macierzy kowariancji, przesuńmy wszystkie wartości oczekiwane o wielkość 3 w górę – rodzaj przesunięcia równoległego stóp, pojęcia występującego m. in. w kursie Inżynierii Finansowej. Tzn. rozważamy teraz model Markowitza

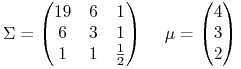$\Sigma=\begin{pmatrix}19&6&1\\ 6&3&1\\ 1&1&\frac{1}{2}\end{pmatrix}\,\quad\mu=\begin{pmatrix}4\\ 3\\ 2\end{pmatrix}$

(14.14)

wzbogacony o stopę wolną od ryzyka $\mu _{0}$ zmieniającą się od 0 do $\frac{33}{13}$ . Te wartości graniczne stopy bezryzykownej są uzasadnione geometrią przykładu i są po prostu wysokościami, na których styczne do granicy minimalnej w obrazach portfeli $e_{3}$ i $e_{1}$ przecinają pionową oś $\overrightarrow{OE}$ . (W samym przykładzie Krzyżewskiego przedział wartości dla stopy bezryzykownej zaczynałby się w $-3$ — dość nieciekawej stopie zwrotu pozbawionej ryzyka.)

Wiemy, że i tutaj cała granica minimalna jest efektywna, bo to stary przykład Krzyżewskiego, tylko ,,kopnięty” o 3 w górę. Portfele optymalne przy zmienianiu stopy $\mu _{0}$ przebiegają więc całą łamaną wierzchołkową, która jest, oczywiście, identyczna jak w przykładzie Krzyżewskiego – patrz Rysunek 7.5 w Wykładzie VII.

Gdy więc przejeżdżamy wartością $\mu _{0}$ przedział $[0,\, 3]$ , wtedy portfele optymalne $\widetilde{x}_{{\text{op}}}$ jadą (bądź stoją) kolejno po (w) częściach łamanej z Rysunku 7.5 położonych na ścianach: (a) $\{ 3\}$ , (b) $\{ 1,\, 3\}$ , (c) $\{ 1,\, 2,\, 3\}$ , (d) $\{ 2,\, 3\}$ , (e) $\{ 2\}$ , (f) $\{ 1,\, 2\}$ , (g) $\{ 1\}$ .
Skomentujemy prawdziwe ruchy portfela optymalnego oraz jego postój w wierzchołku $e_{2}$ . Nie przytaczamy szczegółowych obliczeń – mogą to być (bardzo zalecane) dla czytelnika ćwiczenia sprawdzające.

Ad (b). Dzieje się tak dla $0<\mu _{0}\le\frac{17}{13}$ , zaś wartość oczekiwana portfela optymalnego $\widetilde{E}_{{\text{op}}}$ zmienia się wtedy między 2 i $\frac{36}{17}$ . Sam zaś ten portfel to

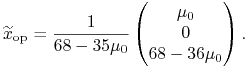$\widetilde{x}_{{\text{op}}}=\frac{1}{68-35\mu _{0}}\begin{pmatrix}\mu _{0}\\ 0\\ 68-36\mu _{0}\end{pmatrix}.$

Jego składowe są wyrażone funkcjami wymiernymi (homografiami) od $\mu _{0}$ . Jest to całkiem naturalne, bo przecież jego wartość oczekiwana jest pewną homografią od $\mu _{0}$ .

Ad (c). Dzieje się tak dla $\frac{17}{13}<\mu _{0}<\frac{4}{3}$ , zaś $\widetilde{E}_{{\text{op}}}$ zmienia się wtedy między $\frac{36}{17}$ i $\frac{7}{3}$ . Natomiast

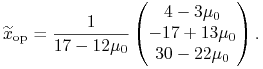$\widetilde{x}_{{\text{op}}}=\frac{1}{17-12\mu _{0}}\begin{pmatrix}4-3\mu _{0}\\ -17+13\mu _{0}\\ 30-22\mu _{0}\end{pmatrix}.$

Ad (d). Dzieje się tak dla $\frac{4}{3}\le\mu _{0}<\frac{3}{2}$ , zaś $\widetilde{E}_{{\text{op}}}$ zmienia się wtedy między $\frac{7}{3}$ i 3. Natomiast

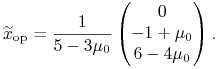$\widetilde{x}_{{\text{op}}}=\frac{1}{5-3\mu _{0}}\begin{pmatrix}0\\ -1+\mu _{0}\\ 6-4\mu _{0}\end{pmatrix}.$

Ad (e). Portfel optymalny stoi na $e_{2}$ , podczas gdy $\mu _{0}$ rośnie od $\frac{3}{2}$ do 2. Dostajemy proste nadstyczne w punkcie $\mathcal{M}(e_{2})$ do granicy efektywnej, wszystko oczywiście w aspekcie M. ( $\mathcal{M}(e_{2})$ jest punktem załamania – kinkiem – na granicy minimalnej.)

Ad (f). Dzieje się tak dla $2<\mu _{0}<\frac{33}{13}$ , zaś $\widetilde{E}_{{\text{op}}}$ zmienia się wtedy między 3 i 4. Natomiast

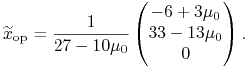$\widetilde{x}_{{\text{op}}}=\frac{1}{27-10\mu _{0}}\begin{pmatrix}-6+3\mu _{0}\\ 33-13\mu _{0}\\ 0\end{pmatrix}.$

Spróbujmy raz jeden zobrazować wszystkie te portfele optymalne dynamicznie na jednym wspólnym rysunku, na osi odciętych odkładając wartości $\mu _{0}$ , zaś na pionowych prostych, nad odpowiednimi wartościami stopy $\mu _{0}$ , zaznaczając różnymi kolorami wkłady odpowiednich walorów do portfela optymalnego. Konkretnie: kolorem ciemnozielonym zaznaczając wkład waloru 1, czerwonym – waloru 2, niebieskim – waloru 3. Oto wynik takiego obrazowania:

[w wersji pdf chochlik drukarski przerzucił diagram na następną stronę]

$\par$

Rys. 14.1. Diagram wyglądałby trochę inaczej – jak? – gdyby na osi odciętych odkładać wartości $\widetilde{E}_{{\text{op}}}$ zamiast $\mu _{0}$ .

Łamana efektywna jest tu, jak wiemy, bardzo bogata. Jej wizualizacja graficzna podana w funkcji parametru $\mu _{0}$ trochę rozczarowuje – widać chyba mniej, niż na Rysunku 7.5. W ramach porównywania tamtego rysunku z obecnym Rysunkiem 14.1, można zadać sobie pytanie (oczywiście kontrolne), czy na obecnym umiemy wskazać punkty, w których, na dawnym, prosta krytyczna przecina boki sympleksu standardowego.
Jest to nietrudne w przypadku portfela krytycznego niemającego waloru numer 2 ( $x_{2}=0$ ): nad odciętą $\mu _{0}=\frac{17}{13}$ widzimy charakterystyczny punkt potrójny.⁵³może komuś przypominają się lekcje fizyki w liceum, np punkt potrójny wody …
Jest to trudniejsze w przypadku portfela krytycznego niemającego waloru numer 1 ( $x_{1}=0$ ). Czytelnik widzi na pewno lekki kink na Rysunku 14.1 na granicy między obszarami niebieskim i czerwonym. Ma on odciętą $\mu _{0}=\frac{4}{3}$ i rzędną $\frac{2}{3}$ . Taką samą odciętą $\frac{4}{3}$ ma punkt o rzędnej 1 – wspólny punkt narożny obszarów: małego zielonego i czerwonego. Oba wymienione punkty trzeba myślowo skleić ze sobą; dostanie się wtedy drugi punkt potrójny na diagramie.

Ćwiczenie 14.4

Dokonujemy przesunięcia równoległego wszystkich wartości oczekiwanych o wielkość $c$ , $\widetilde{\mu}=\mu+ce$ , nie zmieniając przy tym [odwracalnej] macierzy kowariancji.
$\bullet$ Znaleźć wzory na nowe wielkości ,,greckie” $\widetilde{\alpha}$ , $\widetilde{\beta}$ i $\widetilde{\gamma}$ po takim przesunięciu, a następnie
$\bullet$ sprawdzić, że takie przesunięcie równoległe ma (skądinąd naturalną i oczekiwaną) własność funktorialności

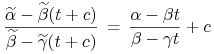$\frac{\widetilde{\alpha}-\widetilde{\beta}(t+c)}{\widetilde{\beta}-\widetilde{\gamma}(t+c)}\,=\,\frac{\alpha-\beta t}{\beta-\gamma t}+c$

dla wszystkich wartości $t\in R$ . (Taka własność funktorialności przebłyskiwała kilka razy w ,,przesuniętym przykładzie Krzyżewskiego” dyskutowanym tuż przed tym ćwiczeniem.)

Łamane wierzchołkowe revisited i początek dyskusji algorytmu CLA

Łamane wierzchołkowe – te odpowiedniki w modelach Markowitza prostych krytycznych Blacka – mogą być, jak już wiemy, bardzo skomplikowane. Szukanie portfeli relatywnie minimalnego ryzyka w modelach Markowitza jest żmudne – porównaj algorytm, czyli de facto metodę prób opisaną w Wykładzie X (bazującą na twierdzeniu Karusha-Kuhna-Tuckera). Również podzbiór łamanej wierzchołkowej – łamana efektywna obsługująca granicę efektywną – może być bardzo złożony, jak pokazują przykłady znalezione przez studentów naszego wydziału⁵⁴P. Grodzki i J. Gruszczyński, patrz też lista osiągnięć studentów podana pod koniec Wykładu VII w roku 2008.

Komentatorzy pracy Markowitza z 1952 czynili mu z tego zarzuty, określając całą rzecz jako mało praktyczną. Jak bowiem w praktyce [wtedy, prawie 60 lat temu] znajdywać tak złożone obiekty? Markowitz odpowiedział artykułem [20] i [pierwszą] książką [21]. Mianowicie ukonkretnił i wyszlifował prawdziwy klejnot, tzw. algorytm prostej krytycznej (Critical Line Algorithm – CLA) zręcznie wyłuskujący te ściany sympleksu, przez które przebiega łamana efektywna, czy łamana wierzchołkowa, zależnie od wariantu.
Należy jednak zaznaczyć, że pierwsze, i od razu przełomowe uwagi na ten temat zawarł on już w [19]! Kluczowa w tym aspekcie jest tam strona 87. Proszę ocenić samej/samemu, reprodukcja poniżej.

[W wersji pdf Rysunek 14.2 jest dopiero pół strony dalej …]

$\par$

Rys. 14.2. A stroke of genius w dolnej części tej strony reprodukowanej z [19].

Natomiast jak po latech oceniał to sam Markowitz? Odpowiedź jest na stronie 38 w jego drugiej książce [22]: `The general portfolio selection model […] was presented in [20], along with the critical line algorithm for computing efficient sets.' Te słowa nie wymagają żadnego dodatkowego komentarza odnośnie pierwszeństwa w odkryciu algorytmu prostej krytycznej w analizie portfelowej.

Przy ilości spółek w modelu $k\approx 200$ , zamiast ogromnej ilości ścian do rozważenia, algorytm CLA zwykle wskazuje tych kilkaset istotnych, na których dzieje się wszystko, co ważne dla analizy portfelowej i decyzji inwestycyjnych o nią opartych.
(W [22] na stronie 157 czytamy: `Fortunately we can find these few hundred [critical lines], and their efficient portions, without enumerating all critical lines.')

W naszym opisie algorytmu CLA będziemy stale zakładać, że $\Sigma>0$ i (5.2). Potem dojdą jeszcze inne niezbędne założenia. Wszystko polegać będzie na zręcznym, innym niż do tej pory szukaniu portfeli relatywnie minimalnego ryzyka $x_{E}$ bez eksponowania parametru $E$ .

Zanim to ukonkretnimy i rozwiniemy, chcemy jeszcze przywołać słowa Sharpe'a z [26]. Zamiast bardzo długiego w tym przypadku cytatu, oto dwie odpowiednie strony z tamtej pracy. Ich lektura, i to teraz, dosłownie na poczekaniu, może być dla czytelnika pierwszym spotkaniem i pochyleniem się nad algorytmem Markowitza. Wyjaśnienia, które nastąpią później, w tym i w następnym (ostatnim) wykładzie, będą inaczej odbierane, gdy czytelnik będzie coś pamiętał ze wstępnego opisu Sharpe'a.

[W wersji pdf idący teraz Rysunek 14.3 przeskoczył aż na następną stronę, zaś zaraz po nim idący Rysunek 14.4 – na jeszcze następną. Zapoznać się z nimi należy przed zagłębieniem się w konkrety opisu algorytmu.]

$\par$

Rys. 14.3. Markowitz otrzymuje tutaj swoje credits.

$\par$

Rys. 14.4. Sedno konstrukcji; można i należy to porównywać z tekstem w dolnej części Rysunku 14.2.

Zagłębiamy się już teraz w konkrety opisu algorytmu. Przypuśćmy, że szukamy takich portfeli na ścianie $\text{IN}\subset\{ 1,\, 2,\dots,\, k\}$ , $\#(\text{IN})\ge 1$ (wierzchołki sympleksu są teraz dopuszczalne!), tzn. rozwiązujemy zagadnienie

$x_{i}>0\,,\quad\big(\Sigma x+\lambda e-\lambda _{E}\mu\big)_{i}=0\quad\text{ dla }i\in\text{IN}\,,$

(14.15)

$x_{j}=0\,,\quad\big(\Sigma x+\lambda e-\lambda _{E}\mu\big)_{j}\ge 0\quad\text{ dla }j\in\text{OUT}=\{ 1,\, 2,\dots,\, k\}\,\,\backslash\,\,\text{IN}$

(14.16)

przy jakichś rzeczywistych $\lambda,\,\lambda _{E}$ zależnych od szukanego $x$ . Markowitz doszedł do wniosku, że $\lambda _{E}$ należy traktować jako niezależny parametr oraz szukał pełnego układu $k$ równań, a nie jedynie $\#(\text{IN})$ równań. Sztuczne $\#(\text{OUT})$ równań wprowadził on w zaskakująco prosty sposób.

Definicja 14.1

Niech $e_{{\text{IN}}}$ , $\mu _{{\text{IN}}}$ to nowe wektory o $k$ współrzędnych, tożsame z $e,\,\mu$ na miejscach z IN, lecz zerowe na miejscach z OUT. Niech $\Sigma _{{\text{IN}}}$ to macierz $k\times k$ , której $(i,\, j)$ -ty wyraz to

$\left\{\begin{array}[]{ll}(i,\, j)\text{-ty wyraz }\Sigma&\hbox{gdy $(i,\, j)\in\text{IN}\times\text{IN}$,}\\ 1&\hbox{gdy $i=j\in\text{OUT}$,}\\ 0&\hbox{gdy $i\ne j,\ (i,\, j)\notin\text{IN}\times\text{IN}$.}\end{array}\right.$

(Proszę porównać te nowe symbole z innymi symbolami $e^{{\text{IN}}}$ , $\mu^{{\text{IN}}}$ , $\Sigma^{{\text{IN}}}$ wprowadzonymi i używanymi w Wykładzie X.)

Równania (14.15) zapisujemy teraz jako układ

$\Sigma _{{\text{IN}}}x+\lambda e_{{\text{IN}}}\,=\,\lambda _{E}\mu _{{\text{IN}}},$

do którego dołączamy równanie budżetowe $e^{{\text{T}}}_{{\text{IN}}}x=1$ . Łącznie dostajemy układ $k+1$ równań z $k+1$ ,,niewiadomymi”, wśród których jest $\#(\text{OUT})$ wiadomych $x_{j}=0,\ j\in\text{OUT}$ :

$\begin{pmatrix}\Sigma _{{\text{IN}}}&e_{{\text{IN}}}\\ e_{{\text{IN}}}^{{\text{T}}}&0\end{pmatrix}\begin{pmatrix}x\\ \lambda\end{pmatrix}=\begin{pmatrix}\lambda _{E}\mu _{{\text{IN}}}\\ 1\end{pmatrix}.$

(14.17)

W podejściu Markowitza kluczowe są macierze $M_{{\text{IN}}}\overset{\text{def}}{=}\left(\begin{smallmatrix}\Sigma _{{\text{IN}}}&e_{{\text{IN}}}\\ e_{{\text{IN}}}^{{\text{T}}}&0\end{smallmatrix}\right)$ układów równań (14.17).

Twierdzenie 14.4

Gdy $\Sigma>0$ oraz (10.3) (tzn. wszystkie liczby $\mu _{1},\,\mu _{2},\dots,\,\mu _{k}$ są różne), wtedy wszystkie macierze $M_{{\textrm{IN}}}$ są odwracalne dla $\textrm{IN}\,\colon\ 1\le\#(\text{IN})\le k$ .

Jest to widoczne bezpośrednio dla IN jednoelementowych. Istotnie, gdy $\text{IN}=\{ i\}$ , wtedy, rozwijając⁵⁵rozwinięcie Laplace'a wyznacznik względem $i$ -go wiersza, składnik z czynnikiem $\sigma _{{ii}}$ znika i zostaje tylko

$\det M_{{\text{IN}}}\,=\,(-1)^{{i+k}}\begin{array}[]{|c|c|}\overbrace{\begin{array}[]{ccc}1&&\text{{\Large{0}}}\\ &\ddots&\\ \text{{\Large{0}}}&&1\end{array}}^{{i-1}}&\overbrace{\begin{array}[]{ccccc}&&&&\\ &&\text{{\Huge{0}}}&&\\ &&&&\end{array}}^{{k-i}}\\ \hline\begin{array}[]{ccc}\\ \\ &\text{{\Huge{0}}}&\\ \\ \\ \end{array}&\begin{array}[]{ccccc}0&1&0&\cdots&0\\ \vdots&&1&\text{{\Huge{0}}}&\vdots\\ \vdots&&&\ddots&0\\ 0&\text{{\Huge{0}}}&&&1\\ 1&0&\cdots&&0\\ \end{array}\end{array}=(-1)^{{i+k}}(-1)^{{k-i+1}}\cdot 1=-1\,,$

a więc ten wyznacznik nie zależy nawet od wariancji $\sigma _{{ii}}=\sigma _{i}^{{\, 2}}$ .

Dla IN więcej niż jednoelementowych potrzeba tu więcej pracy. Na ścianie IN rozwijamy teorię Blacka przy danych $\Sigma^{{\text{IN}}}$ , $\mu^{{\text{IN}}}$ , $e^{{\text{IN}}}$ – patrz wspomniane starsze oznaczenia z Wykładu X. (Oczywiście wykorzystujemy tutaj założenia $\Sigma>0$ oraz $\ne\big(\mu _{1},\,\mu _{2},\dots,\,\mu _{k}\big)$ , czyli założenie (10.3), właśnie jeszcze z Wykładu X; jest to centralny moment dowodu.)

Niech liczby $\alpha,\,\beta,\,\gamma$ pojawiające się w tej teorii będą teraz nazwane $A,\, B,\, C$ i, konsekwentnie,

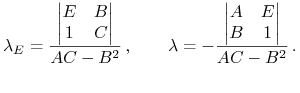$\lambda _{E}=\frac{\begin{vmatrix}E&B\\ 1&C\end{vmatrix}}{AC-B^{2}}\,,\qquad\lambda=-\frac{\begin{vmatrix}A&E\\ B&1\end{vmatrix}}{AC-B^{2}}\,.$

(14.18)

Pytamy się, czy układ $k+1$ równań (14.17) ma rozwiązanie. W czystym sensie wyjętym z GALu, bez żadnego związku z analizą portfelową. To pytanie jest jednak źle postawione – trzeba najpierw sprecyzować wartość $\lambda _{E}$ w kolumnie wyrazów wolnych! Sprecyzujmy więc, biorąc np $E=0$ . Wtedy z (14.18) dostajemy $\lambda _{E}=\frac{B}{B^{2}-AC}$ i równocześnie $\lambda=\frac{A}{B^{2}-AC}$ . Jaki wektor $x$ mógłby dopełnić tę wartość $\lambda$ do rozwiązania w sensie z GALu układu (14.17)? Oczywiście portfel Blacka $x^{{\text{IN}}}(0)$ – porównaj podstawowy wzór (6.2) – uzupełniony zerami na miejscach OUT, by dostać portfel $x\in H\subset\mathbb{R}^{k}$ (!)

Układ równań po doprecyzowaniu ma więc rozwiązanie.

Przypuśćmy teraz, że istnieją dwa różne rozwiązania, cały czas w sensie z GALu, tego układu po doprecyzowaniu, $\left(\begin{smallmatrix}x\\ \lambda\end{smallmatrix}\right)$ , $\left(\begin{smallmatrix}x^{{\prime}}\\ \lambda^{{\prime}}\end{smallmatrix}\right)$ .
Natura równań (14.17) jest taka, że $x,\, x^{{\prime}}$ leżą w płaszczyźnie ściany IN: $x_{j}=x^{{\prime}}_{j}=0$ dla $j\in\text{OUT}$ . Wtedy także $x\ne x^{{\prime}}$ (bo, wobec

$\lambda e_{{\text{IN}}}=\lambda _{E}\mu _{{\text{IN}}}-\Sigma _{{\text{IN}}}x\,,$

równość $x=x^{{\prime}}$ pociągałaby $\lambda=\lambda^{{\prime}}$ ). W takiej sytuacji wspomniana teoria Blacka na ścianie IN ma dwa różne rozwiązania $x$ i $x^{{\prime}}$ przy jednej wartości oczekiwanej $E=0$ . Dwa różne portfele relatywnie minimalnego ryzyka w aspekcie B odpowiadające ustalonej wartości oczekiwanej $E$ ! (Punkty $x$ , $x^{{\prime}}$ rozumiane są teraz jako punkty w przestrzeni $\#(\text{IN})$ -wymiarowej; $\#(\text{IN})\ge 2$ jest, przypominamy to jeszcze raz, istotne.)
Tak, jak dobrze wiadomo, być nie może. Przypuszczenie o dwóch różnych rozwiązaniach jest więc fałszywe. Skoro układ równań liniowych (14.17), po doprecyzowaniu $E=0$ , ma jedno jedyne rozwiązanie w sensie z GALu, jego macierz $M_{{\text{IN}}}$ jest nieosobliwa.

∎

Korzystamy teraz z Twierdzenia 14.4 i rozwiązujemy układ (14.17), lecz teraz już przy dowolnej ustalonej wartości $\lambda _{E}$ (takie to added values oferuje nam za darmo GAL; ktoś inny powie w tym miejscu, że jest to alfabet matematyki):

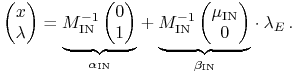$\begin{pmatrix}x\\ \lambda\end{pmatrix}=\underset{\alpha _{{\text{IN}}}}{\underbrace{M_{{\text{IN}}}^{{-1}}\begin{pmatrix}0\\ 1\\ \end{pmatrix}}}+\underset{\beta _{{\text{IN}}}}{\underbrace{M_{{\text{IN}}}^{{-1}}\begin{pmatrix}\mu _{{\text{IN}}}\\ 0\\ \end{pmatrix}}}\cdot\lambda _{E}\,.$

(14.19)

Tak zdefiniowane $\alpha _{{\text{IN}}}$ oraz $\beta _{{\text{IN}}}$ są to wektory o $k+1$ składowych (!), które będą używane w każdym danym etapie IN algorytmu CLA. Lecz nie tylko one.

Obok nich używane będą jeszcze dwa inne wektory, tym razem o $k$ składowych, bezpośrednio związane z nierównościami (14.16).

Definicja 14.2

$\eta:=\Sigma x+\lambda e-\lambda _{E}\mu$

(podstawowy wektor używany podczas stosowania twierdzenia K-KT do poszukiwania portfeli relatywnie minimalnego ryzyka).

Zapisujemy ten wektor $\eta$ trochę inaczej, używając rozwinięcia (14.19):

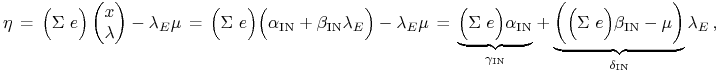$\eta\,=\,\Big(\Sigma\,\, e\Big)\begin{pmatrix}x\\ \lambda\end{pmatrix}-\lambda _{E}\mu\,=\,\Big(\Sigma\,\, e\Big)\Big(\alpha _{{\text{IN}}}+\beta _{{\text{IN}}}\lambda _{E}\Big)-\lambda _{E}\mu\,=\,\underset{\gamma _{{\text{IN}}}}{\underbrace{\Big(\Sigma\,\, e\Big)\alpha _{{\text{IN}}}}}+\underset{\delta _{{\text{IN}}}}{\underbrace{\bigg(\Big(\Sigma\,\, e\Big)\beta _{{\text{IN}}}-\mu\bigg)}}\,\lambda _{E}\,,$

(14.20)

gdzie $\Big(\Sigma\,\, e\Big)$ nie jest wynikiem działania macierzy $\Sigma$ na wektorze $e$ , tylko niekwadratową macierzą $k\times(k+1)$ .

Algorytm CLA to, na każdym etapie IN, dosyć zręczne żonglowanie rozwinięciami (14.19) i (14.20). Dla większej przejrzystości, w dalszym ciągu opuszczać będziemy subskrypty IN w wektorach $\alpha _{{\text{IN}}},\,\beta _{{\text{IN}}},\,\gamma _{{\text{IN}}},\,\delta _{{\text{IN}}}$ . Istnieje ryzyko kolizji oznaczeń z symbolami w teorii Blacka i współautorów, lecz zawsze należy zwracać uwagę na kontekst pojawienia się danego symbolu.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Analiza Portfelowa i Rynki Kapitałowe 1

14. Wykład XIV, 15.I.2010

Twierdzenie 14.1 (Karush; Kuhn, Tucker; wersja znacznie późniejsza, w kategorii pseudo-wypukłej)

Przykład 14.1

Uwaga 14.1

Uwaga 14.2

Twierdzenie 14.2

Ćwiczenie 14.1

Twierdzenie 14.3

Uwaga 14.3 (po dowodzie)

Ćwiczenie 14.2

Ćwiczenie 14.3 (kontynuacja Ćwiczenia 14.2)

Ćwiczenie 14.4

Definicja 14.1

Twierdzenie 14.4

Definicja 14.2