4. Wykład IV, 23.X.2009
Pod koniec poprzedniego wykładu poznaliśmy pojęcie krytycznej wartości współczynnika korelacji, oczywiście w danym modelu Markowitza w wymiarze dwa, a także wartości podkrytycznych i nadkrytycznych tego współczynnika.
Ćwiczenie 4.1
Prześledzić na Rysunku 3.4 (Wykład III), które narysowane tam gałęzie hiperbol odpowiadają wartościom współczynnika korelacji jakiego typu. (Widać tam wyraźnie hiperbolę z krytycznym współczynnikiem korelacji. Które z pozostałych hiperbol mają korelacje podkrytyczne, które zaś nadkrytyczne?)
Aby jeszcze utrwalić pojęcie krytycznej wartości współczynnika korelacji,
Ćwiczenie 4.2
Wyprowadzić wzór na ![]() bezpośrednio z formuły
bezpośrednio z formuły
![]() w Wykładzie III.
w Wykładzie III.
Czubek hiperboli (3.4) będzie znajdował się na wysokości
![]() (tzn. będzie obrazem portfela
(tzn. będzie obrazem portfela ![]() ) lub na wysokości
) lub na wysokości ![]() (tzn. będzie obrazem portfela
(tzn. będzie obrazem portfela ![]() ) wtedy i tylko wtedy, gdy funkcja
dana wzorem
) wtedy i tylko wtedy, gdy funkcja
dana wzorem ![]() w Wykładzie III będzie miała minimum w
w Wykładzie III będzie miała minimum w ![]() lub w
lub w ![]() .
.
Rozwijając wskazówkę i używając wzoru na ![]() z Wykładu III,
musi być albo
z Wykładu III,
musi być albo
co po prostych przekształceniach daje
czyli
albo też
co od razu prowadzi do
-
Komentarz do pierwszego ćwiczenia: widać wyraźnie, że tylko dla
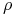 podkrytycznych ryzyko w modelu Markowitza można zmniejszać poniżej wartości
podkrytycznych ryzyko w modelu Markowitza można zmniejszać poniżej wartości
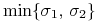 . Ta własność mogłaby też być definicją
podkrytyczności: wartość
. Ta własność mogłaby też być definicją
podkrytyczności: wartość 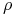 jest podkrytyczna w danym modelu
Markowitza, gdy kres dolny ryzyk portfeli w tym modelu jest mniejszy
od
jest podkrytyczna w danym modelu
Markowitza, gdy kres dolny ryzyk portfeli w tym modelu jest mniejszy
od 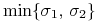 .
.
-
Uwaga nt kanonicznych hiperbol (3.4) w Wykładzie III. Należy mocno podkreślać, że te hiperbole należą do pęku hiperbol zaczepionych w dwóch punktach i przy tym są wszystkie położone kanonicznie. Ze zmianą parametru
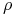 zmienia się,
jak to już badaliśmy, punkt przecięcia ich asymptot oraz kąt rozwarcia asymptot.
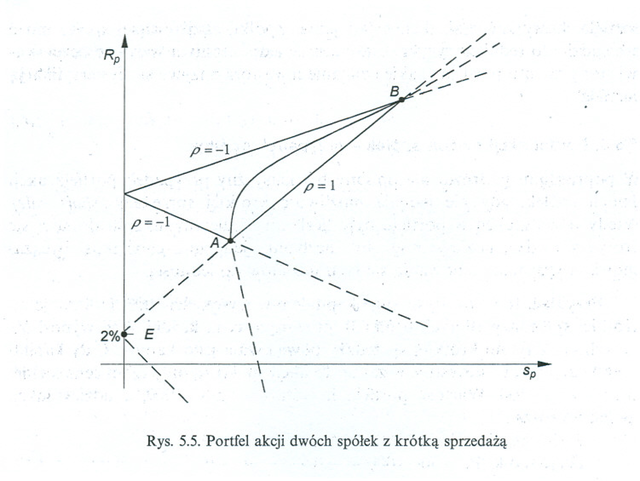
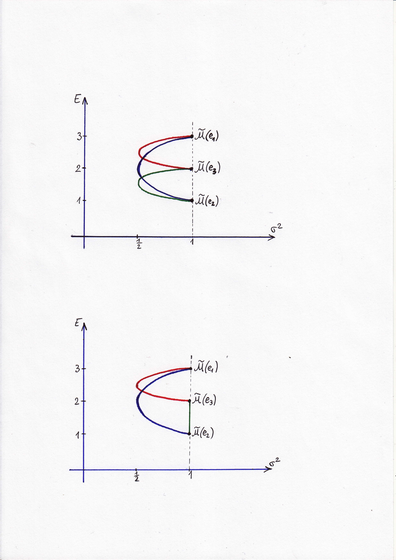
Jednak kanoniczne położenie pozostaje! Poniżej przytoczone są kopie rysunków
z podręcznika [10], które nie respektują kanoniczności położenia hiperbol
w takim pęku.
zmienia się,
jak to już badaliśmy, punkt przecięcia ich asymptot oraz kąt rozwarcia asymptot.
Jednak kanoniczne położenie pozostaje! Poniżej przytoczone są kopie rysunków
z podręcznika [10], które nie respektują kanoniczności położenia hiperbol
w takim pęku.
Pod pierwszym z rysunków zmieniony jest oryginalny podpis, bo jeszcze nie wiemy, co to jest krótka sprzedaż. Na rysunku powinna być jedna z kanonicznie położonych hiperbol (3.4) z Wykładu III.
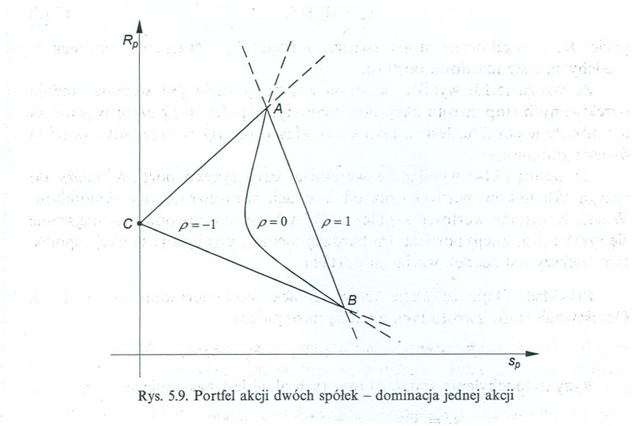
Pod drugim z rysunków też zmieniony jest podpis. (Na nim także rzędna punktu
przecięcia asymptot hiperboli wypadałaby poza przedział ![]() .)
.)
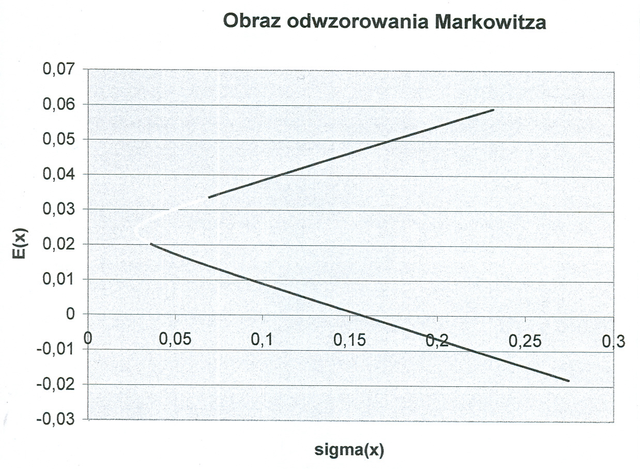
Na koniec tej części proponujemy czytelnikowi zastanowić się nad zdegenerowanym
przypadkiem ![]() , który dotąd (od samego początku) wykluczaliśmy.
, który dotąd (od samego początku) wykluczaliśmy.
Ćwiczenie 4.3
Zanalizować zależność obrazu ![]() odwzorowania Markowitza
od
odwzorowania Markowitza
od ![]() w sytuacji
w sytuacji ![]() (
(![]() i
i ![]() mogą być równe lub różne – bez znaczenia; przyjąć na przykład, że są różne).
mogą być równe lub różne – bez znaczenia; przyjąć na przykład, że są różne).
Dwa techniczne aspekty w analizie portfelowej: hiperbole i parabole.
Pamiętamy, że równanie (3.4) w Wykładzie III to równanie hiperboli, czasami
zdegenerowanej, i że w takiej hiperboli w analizie portfelowej interesująca
jest tylko prawa gałąź położona w półpłaszczyźnie ![]() (i wręcz, w
podejściu Markowitza, tylko niewielka część tej gałęzi). To samo równanie staje
się równaniem paraboli, gdy spojrzymy na nie jako wiążące zmienne z płaszczyzny
(i wręcz, w
podejściu Markowitza, tylko niewielka część tej gałęzi). To samo równanie staje
się równaniem paraboli, gdy spojrzymy na nie jako wiążące zmienne z płaszczyzny
![]() . Pamiętamy też, że w tę płaszczyznę idzie zmodyfikowane
odwzorowanie Markowitza
. Pamiętamy też, że w tę płaszczyznę idzie zmodyfikowane
odwzorowanie Markowitza ![]() . Jak ogólnie wiążą się
ze sobą hiperbole i parabole?
. Jak ogólnie wiążą się
ze sobą hiperbole i parabole?
To temat niemal bez dna. Z wielu dostępnych wątków wybieramy hasło ,,stożkowa” w encyklopedii WSiP-u [w wersji pdf odpowiedni rysunek jest dopiero na następnej stronie]:
Ćwiczenie 4.4
Czy każde dwie hiperbole na płaszczyźnie są podobne?
Nie, oczywiście nie; kąt między asymptotami hiperboli jest niezmiennikiem przy podobieństwach płaszczyzny. (Czy to jest jedyny niezmiennik, czy też jest jeszcze coś?)
To nie było trudne ćwiczenie. Jednak ma ono swoje drugie dno. Mianowicie asymptoty hiperboli zakodowane są niejako w niej samej oglądanej z daleka (im dalej, tym lepiej). Czy pamiętamy jeszcze gałąź hiperboli ilustrującej pierwszy przykład w Wykładzie I (Rysunek 1.2)? Ta sama gałąź oglądana z większej odległości wygląda tak [w wersji pdf Rysunek 4.4 jest dopiero dwie strony dalej]:
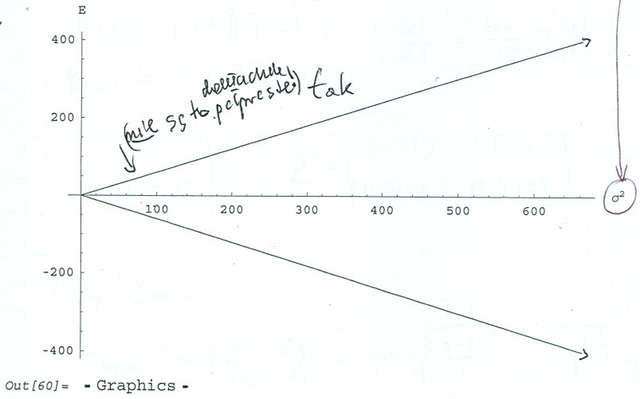
(fragment aktywny w podejściu Markowitza jest jasny i wyróżniony w całym ,,pocisku”). W ten sposób przykład rozpoczynający Wykład I został obejrzany i z bliska i z daleka. Zaczynamy już odczuwać w samej hiperboli obecność jej asymptot, prawda? Zróbmy jeszcze analogiczną rzecz z przykładem ,,5 stanów giełdy” z Wykładu II, który, przypomnijmy, z bliska już był ilustrowany na Rysunku 2.1 (tylko fragment ważny w podejściu Markowitza). Ten sam przykład oglądany z bardzo daleka wygląda następująco (cała gałąź, nie tylko fragment Markowitza; w wersji pdf Rysunek 4.5 jest dopiero dwie strony dalej):
Jest to wycinek oryginalnej pracy studenckiej; sam student dopisał na swoim
wykresie, że `nie są to półproste' (tylko oglądane z daleka wąsy
hiperboli! Omyłkowo też nazwał poziomą oś ![]() zamiast
zamiast ![]() .)
Z daleka sama hiperbola zanika i widzimy (niemal) tylko jej asymptoty.
W dużej skali asymptoty całkowicie dominują hiperbolę.
.)
Z daleka sama hiperbola zanika i widzimy (niemal) tylko jej asymptoty.
W dużej skali asymptoty całkowicie dominują hiperbolę.
Jak to wygląda dla parabol?
Ćwiczenie 4.5
Czy każde dwie parabole na płaszczyźnie są podobne?
Podać np podobieństwo przenoszące parabolę
![]() na parabolę
na parabolę ![]() ,
gdzie
,
gdzie ![]() jest ustalone.
jest ustalone.
Wniosek 4.1
Parabole są bardziej zakręcone i przez to lepiej niż hiperbole będą
w tych wykładach nadawały się do rysunków eksponujących styczności
różnych krzywych. W wielu sytuacjach praktycznych będziemy więc raczej
posługiwali się parabolami (i zmodyfikowanym przekształceniem Markowitza
![]() ) niż hiperbolami (i odzorowaniem Markowitza
) niż hiperbolami (i odzorowaniem Markowitza
![]() ).
).
Seria doświadczeń – zastosowań wzoru (3.4) z Wykładu III.
Przykład 4.1
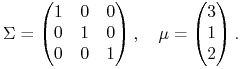 |
Podstawiamy do wzoru (3.4) ![]() ,
, ![]() ,
, ![]() i uzyskujemy obraz boku
i uzyskujemy obraz boku
![]() (oglądany, powtórzmy, na
(oglądany, powtórzmy, na ![]() ).
).
Analogicznie, podstawiając do (3.4) odpowiednie wielkości,
obraz boku ![]() ,
,
obraz boku ![]() .
.
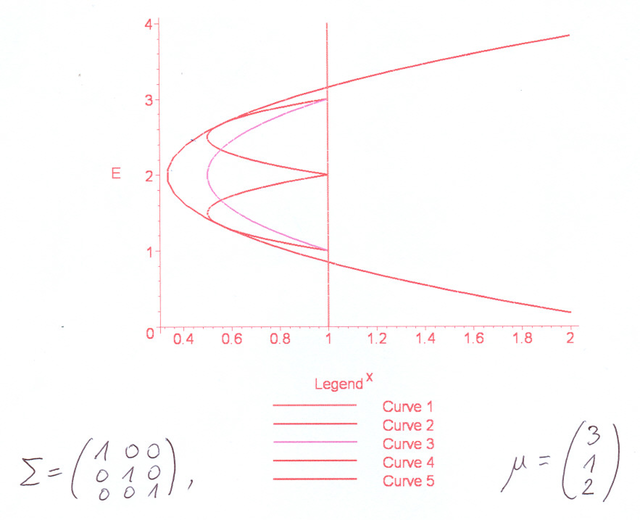
Narysujmy uzyskane parabole na jednym rysunku: pierwszą z nich niebieską, drugą zieloną, trzecią czerwoną (górna część rysunku poniżej). Czujemy, że czegoś tu brakuje do pełnego obrazu; nie bardzo jednak wiemy, czego.
Przykład 4.2
 |
Korzystając z obliczeń już wykonanych w Przykładzie 4.1,
obraz boku ![]() ,
,
obraz boku ![]() .
.
Obraz boku ![]() jest inny. Zgodnie z wiedzą
z Wykładu III, ten obraz ma bardzo proste równanie
jest inny. Zgodnie z wiedzą
z Wykładu III, ten obraz ma bardzo proste równanie ![]() (bo
(bo ![]() oraz
oraz ![]() ).
).
Teraz już możemy narysować wszystkie trzy obrazy na jednym rysunku, analogicznie jak w Przykładzie 4.1 i używając tych samych co tam kolorów (patrz dolna część Rysunku 4.6 powyżej). I tu czegoś brakuje do pełnego obrazu!
Ten brakujący element układanki to punkty krytyczne odwzorowania
które w taki sposób pierwszy scharakteryzował K. Krzyżewski
w wykładach [13], gdzie – uwaga – dziedziną jest teraz cała
płaszczyzna ![]() , a nie tylko sympleks
, a nie tylko sympleks ![]() . To znaczy punkty,
w których rząd pochodnej
. To znaczy punkty,
w których rząd pochodnej ![]() nie jest maksymalny (czyli, tu, jest mniejszy od 2).
nie jest maksymalny (czyli, tu, jest mniejszy od 2).
Należy podkreślić, że o portfelach krytycznych twórcy analizy portfelowej
mówili od samego początku – patrz np strona z pracy [19]
reprodukowana jako Rysunek 14.2 w Wykładzie XIV, albo strona 85 w
tej samej [19] – tylko krytyczność portfela rozumieli
(będąc ekonomistami, nie matematykami) w sensie warunkowej
minimalizacji ryzyka, a nie w sensie AM II. Wybrana tutaj
ahistoryczna (i bardziej matematyczna niż ekonomiczna)
kolejność objaśnień ma, jak się wydaje, zdecydowaną
przewagę dydaktyczną.
Pewien kłopot skrywa się w tym, że ![]() nie jest zbiorem otwartym
w
nie jest zbiorem otwartym
w ![]() , tylko jest rozmaitością kowymiaru 1, zresztą parametryzowaną
jedną jedyną parametryzacją, np
, tylko jest rozmaitością kowymiaru 1, zresztą parametryzowaną
jedną jedyną parametryzacją, np ![]() (mówimy, że
(mówimy, że ![]() jest jednym płatem).
jest jednym płatem).
Trzeba wtedy zapisać ![]() w tej parametryzacji,
policzyć punkty krytyczne takiego odwzorowania, a potem zobaczyć,
jakie punkty odpowiadają im na
w tej parametryzacji,
policzyć punkty krytyczne takiego odwzorowania, a potem zobaczyć,
jakie punkty odpowiadają im na ![]() .
.
Dla Przykładu 4.1 dostajemy w ten sposób
Warunek ![]() oznacza
oznacza ![]() ,
tzn.
,
tzn. ![]() .
.
To w parametrach, zaś na płaszczyźnie ![]() odpowiadają im punkty
odpowiadają im punkty
![]() .
.
Widzimy, że punkty krytyczne w Przykładzie 4.1 tworzą prostą,
zwaną prostą krytyczną. Na tej prostej ![]() ,
,
![]() , stąd
, stąd ![]() ,
,
![]() , co pozwala zapisać obraz
tej prostej przy odwzorowaniu
, co pozwala zapisać obraz
tej prostej przy odwzorowaniu ![]() .
.
Istotnie,
![]() . Jest to zatem obraz
prostej boku
. Jest to zatem obraz
prostej boku ![]() przesunięty w poziomie o
przesunięty w poziomie o
![]() !
!
Teraz dopiero można ,,domknąć” górną część Rysunku 4.6 i – jako wartość
dodaną! – zrozumieć zachowanie odwzorowania ![]() na
na
![]() [w wersji pdf Rysunek 4.7 jest dopiero na następnej stronie].
[w wersji pdf Rysunek 4.7 jest dopiero na następnej stronie].
Obraz prostej krytycznej (będziemy mówili: pocisk Markowitza, tu:
zmodyfikowany pocisk Markowitza) okazuje się styczny: do obrazu
boku ![]() na wysokości
na wysokości ![]() i do obrazu
boku
i do obrazu
boku ![]() na wysokości
na wysokości ![]() . Dlaczego
akurat na takich wysokościach? Bo są to wartości
. Dlaczego
akurat na takich wysokościach? Bo są to wartości ![]() w punktach
przecięcia prostej krytycznej z odpowiednimi bokami:
w punktach
przecięcia prostej krytycznej z odpowiednimi bokami:
![]() ,
,
![]() .
.
Uwaga 4.1
Ktoś może się zapytać, skąd biorą się takie styczności jak na rysunku
powyżej? Dlaczego pocisk Markowitza jest styczny do obrazów boków ciętych
prostą krytyczną? (Te styczności mają, oczywiście, też miejsce na płaszczyźnie
![]() .) Dotykamy tu samej istoty krytyczności. Punkty cięcia
prostych są krytyczne i dlatego w ich obrazach mamy styczności
obrazów prostych. Będziemy do tego wracać w dalszych wykładach i tego
wielokrotnie używać.
.) Dotykamy tu samej istoty krytyczności. Punkty cięcia
prostych są krytyczne i dlatego w ich obrazach mamy styczności
obrazów prostych. Będziemy do tego wracać w dalszych wykładach i tego
wielokrotnie używać.
Ćwiczenie 4.6
Co przekształcenie ![]() w Przykładzie 4.1
robi z trójkątem
w Przykładzie 4.1
robi z trójkątem ![]() ? (Wiemy już, który bok przeprowadza
na który łuk. Jeszcze nie wiemy, który kawałek wnętrza
? (Wiemy już, który bok przeprowadza
na który łuk. Jeszcze nie wiemy, który kawałek wnętrza ![]() przeprowadza na który kawałek płaszczyzny.)
przeprowadza na który kawałek płaszczyzny.)
Analogiczne obliczenia dla Przykładu 4.2, w którym z kolei bardziej
naturalnie jest użyć parametryzacji ![]() , wyglądają następująco.
, wyglądają następująco.
a więc ![]() .
.
Punkty krytyczne odwzorowania ![]() znowu tworzą więc pewną prostą (!)
znowu tworzą więc pewną prostą (!)
![]() , której
, której
![]() -obrazem jest tym razem pionowa
prosta
-obrazem jest tym razem pionowa
prosta ![]() .
.
W świetle powyższych obliczeń, do czego ,,domykają” się wykresy w dolnej części Rysunku 4.6 ?