1. Wykład I, 2.X.2009
Zacznijmy od krótkiego przeglądu faktów z historii giełd na świecie:
-
W roku 1531 w Antwerpii (obecnie w Belgii, wówczas – w odległej prowincji Królestwa Hiszpanii) zostaje otwarta pierwsza giełda (towarowo–pieniężna).
-
W XVII wieku w Nowym Jorku (nazywającym się wówczas Nowym Amsterdamem) wzdłuż jego północnej granicy ciągnął się drewniany płot. W 1652 roku został on zastąpiony wysoką palisadą, wzmacnianą w obawie przed atakiem rdzennych amerykańskich plemion lub Brytyjczyków. W roku 1685 powstały pierwsze plany stworzenia na miejscu palisady ulicy. Z czasem powstający mur (ang. wall ) był wzmacniany, ale już w roku 1699 Brytyjczycy rozebrali fortyfikację; jednak ulica pozostała.
-
Na wolnym powietrzu, na placu przy Exchange Alley w Londynie powstaje giełda londyńska. Przed rokiem 1725 przeniesiono ją do Jonathan's Coffee House, którego nazwę zmieniono na Stock Exchange w roku 1773.
-
W Stanach Zjednoczonych pierwsza zorganizowana giełda powstała w roku 1792, gdy 24 finansistów podpisało stosowne ustalenia (tzw. Buttonwood Agreement). Datę tę uznaje się za moment powstania New York Stock
 Exchange Board.
Exchange Board.
-
W roku 1863 giełda ta zmienia nazwę na New York Stock Exchange, NYSE i przenosi się do majestatycznego budynku przy Wall Street, gdzie pozostaje po dziś dzień.
-
Na przełomie XIX i XX wieku giełda w Nowym Jorku rozwija się: najważniejsze spółki z tamtego okresu to: US Steel, AT
 T, Westinghouse, Eastman Kodak, Procter
T, Westinghouse, Eastman Kodak, Procter  Gamble,
Pillsbury, Sears, Kellogg (niektóre z tych nazw brzmią znajomo
dla współczesnych inwestorów!).
Gamble,
Pillsbury, Sears, Kellogg (niektóre z tych nazw brzmią znajomo
dla współczesnych inwestorów!).
-
28 i 29 października 1929 roku indeks Dow Jones spadł o 69 punktów, osiągając poziom 230 punktów – wartość sprzed kilkudziesięciu lat – wiele osób straciło swój majątek.
-
W roku 1952 Harry M. Markowitz publikuje w The Journal of Finance artykuł ,,Portfolio Selection” [19] – rozpoczyna się epoka współczesnej teorii portfelowej.
Podstawową ideą, leżącą u podstaw analizy portfelowej jest tzw. dywersyfikacja portfela (potocznie formułowana jako zasada: ”don't put all eggs in one basket”), która ma prowadzić do zmniejszania ryzyka (rozumianego jako odchylenie standardowe lub czasem jako wariancja stopy zwrotu z portfela akcji – patrz dalsza część tego wykładu).
Warto też zwrócić uwagę na fakt, iż istnieje teoria stojąca
w całkowitej opozycji do idei dywersyfikacji – jest to tzw.
inwestowanie skoncentrowane (the focus investment strategy ),
polegające na zakupie akcji niewielkiej liczby spółek. Najbardziej
znanym zwolennikiem tej teorii jest Warren Buffett – amerykański
inwestor, znajdujący się w roku 2009 (wg magazynu Forbes)
na drugim miejscu na liście najbogatszych ludzi świata. Jego
strategia polega właśnie na zakupie dużych pakietów akcji kilku
doskonale poznanych przedsiębiorstw. Uważa on, iż takie działanie
umożliwia kontrolowanie zmian tych walorów i dokonywanie
ewentualnych korekt, co byłoby trudniejsze w przypadku portfela z
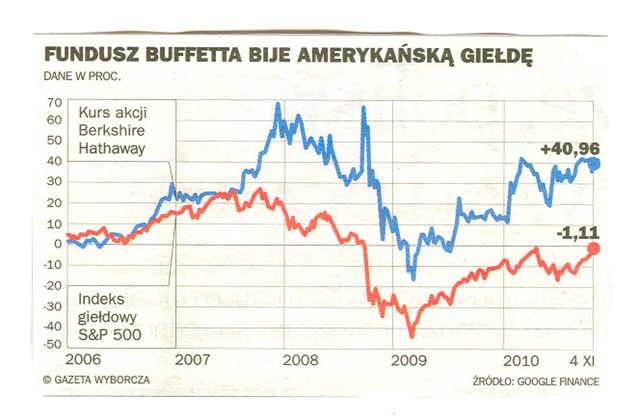
akcjami wielu spółek. Wyniki ogromnego funduszu inwestycyjnego
Berkshire Hathaway zarządzanego przez Buffetta są, także w ostatnich
latach, dobre – patrz zestawienie procentowej zmiany kursu jego
akcji w porównaniu ze zmianą indeksu S![]() P 500 (biorąc za punkt
odniesienia początek roku 2006) przytoczone tu poniżej.
P 500 (biorąc za punkt
odniesienia początek roku 2006) przytoczone tu poniżej.
Tak więc wywodząca się od Markowitza analiza portfelowa nie jest
jedyną strategią dostępną graczom giełdowym. Zostawiając teraz na
boku wielkiego inwestora (który w pierwszych tygodniach obecnego
kryzysu kupował jesienią 2008 za 8 miliardów dolarów akcje
Goldman ![]() Sachs i General Electric), wracajmy do idei,
które upowszechnił Markowitz. Wprowadzimy mianowicie ideę
opisu i mierzenia ryzyka przy kupnie akcji. W tym celu
przyjrzyjmy się najpierw następującemu przykładowi.
Sachs i General Electric), wracajmy do idei,
które upowszechnił Markowitz. Wprowadzimy mianowicie ideę
opisu i mierzenia ryzyka przy kupnie akcji. W tym celu
przyjrzyjmy się najpierw następującemu przykładowi.
Wyobraźmy sobie, że możemy zagrać w grę ![]() , polegającą na tym, iż
rzucamy raz symetryczną (uczciwą) monetą i jeśli wypadnie orzeł, to
dostajemy złotówkę, natomiast jeśli wypadnie reszka, to my płacimy
złotówkę. Jest to tzw. gra sprawiedliwa, gdyż szanse wygranej
naszego rywala i nasze są równe (mówiąc nieco inaczej, średnia
wygrana w tej grze jest równa zero). Każdy zapewne zgodziłby się
po krótkim namyśle zagrać w taką grę – możemy się wzbogacić o
złotówkę, a jeśli nawet przegramy, to nic szczególnie strasznego
się nie stanie. Możemy więc uznać, że gra
, polegającą na tym, iż
rzucamy raz symetryczną (uczciwą) monetą i jeśli wypadnie orzeł, to
dostajemy złotówkę, natomiast jeśli wypadnie reszka, to my płacimy
złotówkę. Jest to tzw. gra sprawiedliwa, gdyż szanse wygranej
naszego rywala i nasze są równe (mówiąc nieco inaczej, średnia
wygrana w tej grze jest równa zero). Każdy zapewne zgodziłby się
po krótkim namyśle zagrać w taką grę – możemy się wzbogacić o
złotówkę, a jeśli nawet przegramy, to nic szczególnie strasznego
się nie stanie. Możemy więc uznać, że gra ![]() jest mało ryzykowna.
jest mało ryzykowna.
Dość podobna jest gra ![]() . Również rzucamy raz symetryczną monetą i
jeśli wypadnie orzeł, to dostajemy
. Również rzucamy raz symetryczną monetą i
jeśli wypadnie orzeł, to dostajemy ![]() zł, zaś jeśli wypadnie
reszka, to płacimy
zł, zaś jeśli wypadnie
reszka, to płacimy ![]() zł. I ta gra jest sprawiedliwa - szanse
wygranej są dla każdego z grających takie same. Widać jednak, że
większość osób niechętnie zgodziłaby się zagrać w tę grę.
zł. I ta gra jest sprawiedliwa - szanse
wygranej są dla każdego z grających takie same. Widać jednak, że
większość osób niechętnie zgodziłaby się zagrać w tę grę.
Zadajmy sobie więc pytanie, co różni obie te gry? Co sprawia, że
jedna z nich wydaje się ,,niegroźna”, zaś w drugą zagralibyśmy już
bardzo niechętnie? Bez wątpienia czujemy, że gra ![]() niesie ze sobą
dużo większe RYZYKO – możemy co prawda wiele zyskać, ale również bardzo
dużo stracić. Jak jednak porównać ryzyka, wiążące się z tymi grami?
Wyznaczmy najpierw średnie wygrane w każdej z gier.
niesie ze sobą
dużo większe RYZYKO – możemy co prawda wiele zyskać, ale również bardzo
dużo stracić. Jak jednak porównać ryzyka, wiążące się z tymi grami?
Wyznaczmy najpierw średnie wygrane w każdej z gier.
Wygrana w grze ![]() jest zmienną losową (oznaczmy ją przez
jest zmienną losową (oznaczmy ją przez ![]() ),
przyjmującą dwie wartości: 1 z prawdopodobieństwem
),
przyjmującą dwie wartości: 1 z prawdopodobieństwem ![]() (jest to szansa wyrzucenia orła w rzucie symetryczną monetą) oraz
(jest to szansa wyrzucenia orła w rzucie symetryczną monetą) oraz
![]() (stratę rozumiemy, jako wygraną ujemną) również z prawdopodobieństwem
(stratę rozumiemy, jako wygraną ujemną) również z prawdopodobieństwem
![]() (szansa wyrzucenia reszki). Zatem średnia wygrana w
tej grze będzie wartością oczekiwaną zmiennej losowej, oznaczającej
wygraną w grze
(szansa wyrzucenia reszki). Zatem średnia wygrana w
tej grze będzie wartością oczekiwaną zmiennej losowej, oznaczającej
wygraną w grze ![]() . Wynosi więc ona
. Wynosi więc ona ![]() . Analogicznie
wyznaczamy średnią wygraną w grze
. Analogicznie
wyznaczamy średnią wygraną w grze ![]() . Również wynosi ona 0. Widzimy
stąd, że wielkość średniej wygranej nie rozróżnia w żaden sposób
naszych gier (mówi ona tylko, że obie gry są sprawiedliwe). Kolejną
miarą, odnoszącą się do zmiennych losowych, jest wariancja. Jest to
jedna z tzw. miar rozproszenia. Obliczymy teraz wariancję
wygranej w grze
. Również wynosi ona 0. Widzimy
stąd, że wielkość średniej wygranej nie rozróżnia w żaden sposób
naszych gier (mówi ona tylko, że obie gry są sprawiedliwe). Kolejną
miarą, odnoszącą się do zmiennych losowych, jest wariancja. Jest to
jedna z tzw. miar rozproszenia. Obliczymy teraz wariancję
wygranej w grze ![]() . Jest ona równa
. Jest ona równa ![]() . Wariancja
wygranej w grze
. Wariancja
wygranej w grze ![]() wynosi zaś
wynosi zaś ![]() .
Mamy więc coś, co wyraźnie odróżnia nasze gry! Gra
.
Mamy więc coś, co wyraźnie odróżnia nasze gry! Gra ![]() ma wariancję
malutką, zaś gra
ma wariancję
malutką, zaś gra ![]() olbrzymią. Widać jednak, iż wariancja, jak na
miarę ryzyka związanego z naszymi grami, jest nieco ,,przesadna”.
Gdyby wyciągnąć pierwiastek z wariancji wygranych, otrzymalibyśmy
tzw. odchylenie standardowe (oznacza się je symbolem
olbrzymią. Widać jednak, iż wariancja, jak na
miarę ryzyka związanego z naszymi grami, jest nieco ,,przesadna”.
Gdyby wyciągnąć pierwiastek z wariancji wygranych, otrzymalibyśmy
tzw. odchylenie standardowe (oznacza się je symbolem
![]() ), wynoszące odpowiednio
), wynoszące odpowiednio ![]() i
i ![]() . Widzimy więc, że
jest to w naszym wypadku całkiem niezła miara ryzyka! Nie dość, że
dla mało ryzykownej gry
. Widzimy więc, że
jest to w naszym wypadku całkiem niezła miara ryzyka! Nie dość, że
dla mało ryzykownej gry ![]() przyjmuje małą wartość, zaś dla bardzo
ryzykownej dużą, to jeszcze te wartości są akurat równe możliwej
stracie lub zyskowi (tak jest tylko dla prostej gry symetrycznej).
przyjmuje małą wartość, zaś dla bardzo
ryzykownej dużą, to jeszcze te wartości są akurat równe możliwej
stracie lub zyskowi (tak jest tylko dla prostej gry symetrycznej).
Zastosujmy więc zdobytą wiedzę do analizy ryzyka na giełdzie. Każdy, kto słyszał o giełdzie wie, że najbardziej typowym zajęciem inwestorów jest kupowanie i sprzedawanie akcji wybranych spółek, notowanych na giełdzie. Inwestorzy starają się to robić w ten sposób, aby oczywiście zyskać możliwie dużo. Niektórzy obserwują tylko zmiany kursów akcji i starają się wybierać takie spółki, które np w ostatnim czasie zaczynają zyskiwać na wartości i mają nadzieję, że ta tendencja będzie się utrzymywała w najbliższej przyszłości; inni czekają na moment, kiedy akcje jakiejś spółki znacznie spadną i je kupują, licząc na wzrost ich wartości … Są to najprostsze sposoby, wymagające jedynie obserwacji zmian stóp zwrotu.
Jeżeli na początku ustalonego okresu dana akcja miała notowanie
![]() , zaś na końcu ma, czy będzie miała, notowanie
, zaś na końcu ma, czy będzie miała, notowanie
![]() , to stopą zwrotu w tym okresie nazywa
się stosunek zysku (może on być ujemny!) z zakupu tej akcji do
początkowego jej kursu (zakładamy, że kursy uwzględniają już
ewentualne wypłacane dywidendy). Stopa zwrotu jest zatem równa
, to stopą zwrotu w tym okresie nazywa
się stosunek zysku (może on być ujemny!) z zakupu tej akcji do
początkowego jej kursu (zakładamy, że kursy uwzględniają już
ewentualne wypłacane dywidendy). Stopa zwrotu jest zatem równa
Warto zauważyć, że stopa zwrotu teoretycznie może przyjmować dowolną
wartość nie mniejszą niż ![]() . Najmniejsza wartość
. Najmniejsza wartość ![]() odpowiada
sytuacji, gdy notowanie akcji na końcu interesującego nas okresu
wyniesie 0, czyli gdy stracimy wszystkie zainwestowane pieniądze.
Oczywiście wymyślono rozmaite sposoby przewidywania, kiedy warto
daną akcję kupić, a kiedy sprzedać (są to metody należące do tzw.
analizy technicznej). My jednak przyjrzymy się jeszcze
innemu podejściu do inwestowania na giełdzie. Będzie to spojrzenie
na akcje nie tylko pod kątem stopy zwrotu, ale właśnie
uwzględniające też ryzyko.
odpowiada
sytuacji, gdy notowanie akcji na końcu interesującego nas okresu
wyniesie 0, czyli gdy stracimy wszystkie zainwestowane pieniądze.
Oczywiście wymyślono rozmaite sposoby przewidywania, kiedy warto
daną akcję kupić, a kiedy sprzedać (są to metody należące do tzw.
analizy technicznej). My jednak przyjrzymy się jeszcze
innemu podejściu do inwestowania na giełdzie. Będzie to spojrzenie
na akcje nie tylko pod kątem stopy zwrotu, ale właśnie
uwzględniające też ryzyko.
Jakie ryzyko wiąże się z zakupem akcji? Oczywiście niebezpieczeństwo
spadku ich wartości. Nasuwa się więc pytanie, jak można by zmierzyć
to ryzyko? Przypomnijmy sobie, jak wyglądała sytuacja z grami ![]() i
i
![]() . Ryzykowna była ta gra, która charakteryzowała się dużą
potencjalną stratą, czyli dla której odchylenie możliwych wyników
gry od wartości średniej było duże. Podobnie rzecz się ma z akcjami:
za bardziej ryzykowną uznamy tę, która wykazywała w przeszłości
większe wahania, gdyż występuje wówczas większe niebezpieczeństwo,
że również i teraz, po jej zakupie, zmieni ona gwałtownie swą
wartość (oczywiście dla kupującego groźny jest tylko spadek wartości
akcji). Spróbujmy więc użyć odchylenia standardowego również do
oceny ryzyka inwestowania w akcje. Przy ewentualnych decyzjach
inwestycyjnych będziemy zawsze rozważać jakiś okres inwestycyjny od
chwili bieżącej do ustalonego momentu w przyszłości. Stopa zwrotu
będzie więc zmienną losową: cena
. Ryzykowna była ta gra, która charakteryzowała się dużą
potencjalną stratą, czyli dla której odchylenie możliwych wyników
gry od wartości średniej było duże. Podobnie rzecz się ma z akcjami:
za bardziej ryzykowną uznamy tę, która wykazywała w przeszłości
większe wahania, gdyż występuje wówczas większe niebezpieczeństwo,
że również i teraz, po jej zakupie, zmieni ona gwałtownie swą
wartość (oczywiście dla kupującego groźny jest tylko spadek wartości
akcji). Spróbujmy więc użyć odchylenia standardowego również do
oceny ryzyka inwestowania w akcje. Przy ewentualnych decyzjach
inwestycyjnych będziemy zawsze rozważać jakiś okres inwestycyjny od
chwili bieżącej do ustalonego momentu w przyszłości. Stopa zwrotu
będzie więc zmienną losową: cena ![]() będzie
znana, zaś cena
będzie
znana, zaś cena ![]() – przyszła i nieznana. Parametry
takiej zmiennej losowej będziemy jedynie estymować na
podstawie dotychczasowych notowań akcji spółki.
– przyszła i nieznana. Parametry
takiej zmiennej losowej będziemy jedynie estymować na
podstawie dotychczasowych notowań akcji spółki.
W tym celu należy najpierw wybrać pewien reprezentatywny
z naszego punktu widzenia okres historyczny (np tydzień, miesiąc,
kwartał, rok, pięć lat, ![]() ). Potem estymować czy (o)szacować
oczekiwaną stopę zwrotu na podstawie danych historycznych
nt stóp zwrotu w poszczególnych podokresach (np dniach,
tygodniach, itp) wybranego okresu. Następnie można już szacować
ryzyko akcji, rozumiane jako odchylenie standardowe zmiennej
losowej stopy zwrotu z tych akcji.
). Potem estymować czy (o)szacować
oczekiwaną stopę zwrotu na podstawie danych historycznych
nt stóp zwrotu w poszczególnych podokresach (np dniach,
tygodniach, itp) wybranego okresu. Następnie można już szacować
ryzyko akcji, rozumiane jako odchylenie standardowe zmiennej
losowej stopy zwrotu z tych akcji.
Jeżeli w wybranym okresie historycznym mamy już wyznaczone
![]() wartości stopy zwrotu z danej akcji, wynoszących kolejno
wartości stopy zwrotu z danej akcji, wynoszących kolejno
![]() , to oczekiwaną stopę zwrotu z inwestycji w
tę akcję liczymy (w istocie tylko estymujemy!) jako średnią
arytmetyczną tych wartości. Jest to estymator nieobciążony
wartości oczekiwanej zmiennej losowej stopy zwrotu
, to oczekiwaną stopę zwrotu z inwestycji w
tę akcję liczymy (w istocie tylko estymujemy!) jako średnią
arytmetyczną tych wartości. Jest to estymator nieobciążony
wartości oczekiwanej zmiennej losowej stopy zwrotu ![]() , która w tych
wykładach będzie oznaczana symbolem
, która w tych
wykładach będzie oznaczana symbolem ![]() . Mamy więc wzór
. Mamy więc wzór
![]() . Ten estymator wartości
oczekiwanej
. Ten estymator wartości
oczekiwanej ![]() jest nazywany historyczną oczekiwaną stopą zwrotu.
jest nazywany historyczną oczekiwaną stopą zwrotu.
Natomiast odchylenie standardowe stopy zwrotu szacujemy (estymujemy) ze wzoru
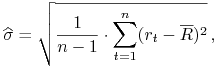 |
gdzie ![]() jest historyczną oczekiwaną stopą zwrotu.
To jest nasz (i przy tym najczęściej używany) estymator odchylenia
standardowego zmiennej
jest historyczną oczekiwaną stopą zwrotu.
To jest nasz (i przy tym najczęściej używany) estymator odchylenia
standardowego zmiennej ![]() , które w tych wykładach będzie oznaczane
symbolem
, które w tych wykładach będzie oznaczane
symbolem ![]() .
.
Załóżmy, że w przeciągu ostatnich dwóch miesięcy cotygodniowe dane na temat kursów dwu spółek X i Y kształtowały się następująco:
| X | ||||||||
|---|---|---|---|---|---|---|---|---|
| Y |
Możemy wyznaczyć więc stopy zwrotu w kolejnych tygodniach. Liczymy
je tak, jak to już zostało wcześniej opisane, np stopa zwrotu dla
spółki ![]() w pierwszym tygodniu wynosi
w pierwszym tygodniu wynosi ![]() , itd. W ten sposób dostajemy ciąg próbek –
tygodniowych stóp zwrotu dla obu spółek (podajemy je w
, itd. W ten sposób dostajemy ciąg próbek –
tygodniowych stóp zwrotu dla obu spółek (podajemy je w ![]() , jak
to się zwykle robi):
, jak
to się zwykle robi):
| X | |||||||
|---|---|---|---|---|---|---|---|
| Y |
Historyczna tygodniowa oczekiwana stopa zwrotu z inwestycji w akcje
spółki X, na podstawie dwumiesięcznego okresu obserwacji, wynosi
więc 3.3315![]() (jest to, powtarzamy, średnia arytmetyczna liczb z
pierwszego wiersza powyższej tabeli). Wyestymowane ryzyko zmiennej
stopy zwrotu z akcji X wyznaczamy w sposób wspomniany już wyżej;
wynosi ono 7.3471
(jest to, powtarzamy, średnia arytmetyczna liczb z
pierwszego wiersza powyższej tabeli). Wyestymowane ryzyko zmiennej
stopy zwrotu z akcji X wyznaczamy w sposób wspomniany już wyżej;
wynosi ono 7.3471![]() . Jeśli chodzi o akcje spółki Y, historyczna
(też tygodniowa) oczekiwana stopa zwrotu z tej inwestycji, na
podstawie wybranego przez nas do obserwacji okresu dwóch miesięcy,
wynosi 2.0415
. Jeśli chodzi o akcje spółki Y, historyczna
(też tygodniowa) oczekiwana stopa zwrotu z tej inwestycji, na
podstawie wybranego przez nas do obserwacji okresu dwóch miesięcy,
wynosi 2.0415![]() , natomiast wyestymowane ryzyko to 3.7591
, natomiast wyestymowane ryzyko to 3.7591![]() .
Widzimy więc, że co prawda akcje spółki X miały w przeciągu
wybranego przez nas historycznego okresu obserwacji większą stopę
zwrotu niż akcje spółki Y, jednak odchylenie standardowe stóp zwrotu
akcji spółki X jest większe. Do inwestora więc należy decyzja, czy
wybrać akcje, charakteryzujące się większą historyczną stopą zwrotu,
ale i większym ryzykiem, czy też zgodzić się na nieco mniejszą stopę
zwrotu w zamian za mniejsze ryzyko. Niestety, w rzeczywistości tak
właśnie najczęściej bywa – im wyższe są stopy zwrotu osiągane przez
akcje, tym większe wiąże się z nimi ryzyko. Podczas dalszych
wykładów poznamy metody porównywania i wyboru walorów ,,lepszych”
w określonym sensie. Jako przedsmak czekających nas tu atrakcji i
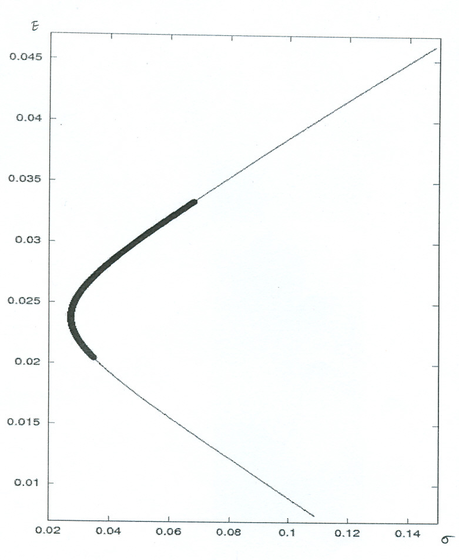
możliwości przytaczamy poniżej wykres zależności ryzyka i wartości
oczekiwanej w tym właśnie przykładzie, tylko rozumianym w szerszym
sensie – gdybyśmy mianowicie zaczęli kombinować czyli
łączyć inwestowanie w akcje spółek X i Y. Możliwe by były wtedy
różne portfele akcji spółek X i Y. Wartości oczekiwane
(pochodzące z estymacji) zmieniałyby się wtedy płynnie między
2.0415
.
Widzimy więc, że co prawda akcje spółki X miały w przeciągu
wybranego przez nas historycznego okresu obserwacji większą stopę
zwrotu niż akcje spółki Y, jednak odchylenie standardowe stóp zwrotu
akcji spółki X jest większe. Do inwestora więc należy decyzja, czy
wybrać akcje, charakteryzujące się większą historyczną stopą zwrotu,
ale i większym ryzykiem, czy też zgodzić się na nieco mniejszą stopę
zwrotu w zamian za mniejsze ryzyko. Niestety, w rzeczywistości tak
właśnie najczęściej bywa – im wyższe są stopy zwrotu osiągane przez
akcje, tym większe wiąże się z nimi ryzyko. Podczas dalszych
wykładów poznamy metody porównywania i wyboru walorów ,,lepszych”
w określonym sensie. Jako przedsmak czekających nas tu atrakcji i
możliwości przytaczamy poniżej wykres zależności ryzyka i wartości
oczekiwanej w tym właśnie przykładzie, tylko rozumianym w szerszym
sensie – gdybyśmy mianowicie zaczęli kombinować czyli
łączyć inwestowanie w akcje spółek X i Y. Możliwe by były wtedy
różne portfele akcji spółek X i Y. Wartości oczekiwane
(pochodzące z estymacji) zmieniałyby się wtedy płynnie między
2.0415![]() i 3.7591
i 3.7591![]() , zaś ryzyka (też pochodzące z estymacji)
czasem schodziłyby nawet poniżej mniejszego z dwóch ryzyk
– tego związanego ze spółką Y ! Teoria, którą niebawem
rozwiniemy za Markowitzem i jego kontynuatorami, prowadzi do
następującej dokładnej zależności między ryzykiem i wartością
oczekiwaną portfela akcji spółek X i Y :
, zaś ryzyka (też pochodzące z estymacji)
czasem schodziłyby nawet poniżej mniejszego z dwóch ryzyk
– tego związanego ze spółką Y ! Teoria, którą niebawem
rozwiniemy za Markowitzem i jego kontynuatorami, prowadzi do
następującej dokładnej zależności między ryzykiem i wartością
oczekiwaną portfela akcji spółek X i Y :
Przeanalizujemy teraz dokładniej zjawisko zasygnalizowane na tym wykresie, rozważając problem inwestycji mieszanych w akcje dwu innych spółek A i B, zupełnie analogicznie do budowania portfela z akcji spółek X i Y branych w różnych proporcjach.
Załóżmy, że odnaleźliśmy notowania takich spółek A i B z ostatnich dwóch miesięcy i na ich podstawie obliczyliśmy 7 tygodniowych stóp zwrotu (w praktyce należałoby wziąć pod uwagę dłuższy okres historyczny – wówczas wyniki możnaby traktować jako bardziej wiarygodne). Otrzymaliśmy następujące dane:
| A | |||||||
|---|---|---|---|---|---|---|---|
| B |
Są to historyczne wartości, które służą, jak już wiemy, do
estymowania parametrów zmiennych losowych stóp zwrotu ![]() i
i ![]() . Historyczna tygodniowa oczekiwana stopa zwrotu z
inwestycji w akcje spółki A, na podstawie wybranego przez nas okresu
dwóch miesięcy, wynosi
. Historyczna tygodniowa oczekiwana stopa zwrotu z
inwestycji w akcje spółki A, na podstawie wybranego przez nas okresu
dwóch miesięcy, wynosi ![]() , zaś dla
spółki B jest to wielkość
, zaś dla
spółki B jest to wielkość ![]() .
Natomiast dla estymatorów ryzyk zmiennych stóp zwrotu
.
Natomiast dla estymatorów ryzyk zmiennych stóp zwrotu ![]() i
i ![]() dostajemy, odpowiednio:
dostajemy, odpowiednio: ![]() ,
, ![]() .
.
Jakie wnioski nasuwają się po obejrzeniu tych wyników? Co prawda
poznaliśmy tylko estymatory nieznanych dokładnie wielkości
![]() ,
,
![]() ,
, ![]() ,
,
![]() , jednak tak jest zawsze
w analizie portfelowej – nigdy nie znamy dokładnych rozkładów
zmiennych stóp zwrotu, porównaj już pierwszą i podstawową pracę
Markowitza [19] ! Wnioskujemy i oceniamy tylko na
podstawie estymatorów
, jednak tak jest zawsze
w analizie portfelowej – nigdy nie znamy dokładnych rozkładów
zmiennych stóp zwrotu, porównaj już pierwszą i podstawową pracę
Markowitza [19] ! Wnioskujemy i oceniamy tylko na
podstawie estymatorów ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
Oczywiście od razu nasuwa się nam wybór akcji spółki A, jako
zdecydowanie lepszej! Wykazuje ona dużą historyczną stopę
zwrotu (25![]() ), podczas gdy akcje spółki B ,,zachowywały się”
fatalnie — przynosiły niemal ciągłe straty, dając ostatecznie
stopę zwrotu
), podczas gdy akcje spółki B ,,zachowywały się”
fatalnie — przynosiły niemal ciągłe straty, dając ostatecznie
stopę zwrotu ![]() ! Co więcej, spółka A może pochwalić się
wahaniami (24.49
! Co więcej, spółka A może pochwalić się
wahaniami (24.49![]() ) zdecydowanie mniejszymi, niż wahania i tak
kiepskiej spółki B (37.41
) zdecydowanie mniejszymi, niż wahania i tak
kiepskiej spółki B (37.41![]() ). Nie ma więc żadnej wątpliwości,
jaką decyzję należy podjąć i nonsensem wydaje się branie pod
uwagę ,,słabej” spółki!
). Nie ma więc żadnej wątpliwości,
jaką decyzję należy podjąć i nonsensem wydaje się branie pod
uwagę ,,słabej” spółki!
Czy rzeczywiście jednak B nic nam nie może zaoferować? Przekonajmy się, że nie jest to wcale takie oczywiste.
Wyobraźmy sobie, że postanowiliśmy w naszej inwestycji uwzględnić
również spółkę B. Oczywiście nie chcemy zrezygnować ze świetnej
spółki A, zatem postanawiamy nabyć akcje obydwu tych spółek.
Inwestorzy nazywają taką sytuację zakupem portfela akcji.
Nasz portfel będzie tylko dwuelementowy. Spróbujmy opisać go w
ścisły sposób. Wystarczy do tego płaszczyzna kartezjańska ![]() .
Nasz portfel to punkt
.
Nasz portfel to punkt ![]() , gdzie
, gdzie ![]() oraz
oraz
![]() będą częściami naszego kapitału, zainwestowanymi w akcje
spółki A oraz B odpowiednio. Widzimy, że
będą częściami naszego kapitału, zainwestowanymi w akcje
spółki A oraz B odpowiednio. Widzimy, że ![]() . Ponadto
sensowne portfele muszą mieć współrzędne nieujemne (najmniejszą
ilością akcji, które możemy kupić, jest zero). Zauważmy, że
wszystkie portfele o tych własnościach tworzą na płaszczyźnie
odcinek, będący fragmentem prostej o równaniu
. Ponadto
sensowne portfele muszą mieć współrzędne nieujemne (najmniejszą
ilością akcji, które możemy kupić, jest zero). Zauważmy, że
wszystkie portfele o tych własnościach tworzą na płaszczyźnie
odcinek, będący fragmentem prostej o równaniu ![]() zawartym między punktami
zawartym między punktami ![]() i
i ![]() .
Tak więc jeżeli rozważamy zakup akcji dwu spółek, to możemy
wybierać spośród nieskończenie wielu portfeli z tego odcinka
— nazywa się go zbiorem portfeli dopuszczalnych.
Np jeżeli mamy do dyspozycji 1000 zł i postanowiliśmy nabyć akcje
spółki A za 850 zł oraz akcje spółki B za 150 zł, nasz portfel ma
postać
.
Tak więc jeżeli rozważamy zakup akcji dwu spółek, to możemy
wybierać spośród nieskończenie wielu portfeli z tego odcinka
— nazywa się go zbiorem portfeli dopuszczalnych.
Np jeżeli mamy do dyspozycji 1000 zł i postanowiliśmy nabyć akcje
spółki A za 850 zł oraz akcje spółki B za 150 zł, nasz portfel ma
postać ![]() . Ściślej rzecz ujmując, jeżeli
posiadamy w chwili początkowej kwotę
. Ściślej rzecz ujmując, jeżeli
posiadamy w chwili początkowej kwotę ![]() i akcje
spółki A zakupimy za
i akcje
spółki A zakupimy za ![]() , zaś akcje spółki B
za
, zaś akcje spółki B
za ![]() , to kapitał końcowy (losowy –
nieznany w chwili początkowej!) wynosić będzie
, to kapitał końcowy (losowy –
nieznany w chwili początkowej!) wynosić będzie ![]() , gdzie
, gdzie ![]() oraz
oraz
![]() to oczywiście zmienne losowe – stopy zwrotu
z akcji spółek A i B.
to oczywiście zmienne losowe – stopy zwrotu
z akcji spółek A i B.
Przez stopę zwrotu z portfela ![]() (wielkość losową!) rozumiemy stosunek (losowego) zysku inwestora
posiadającego dany portfel akcji do kwoty (znanej, nielosowej)
zainwestowanej w ten portfel na początku; jest to więc zmienna
losowa
(wielkość losową!) rozumiemy stosunek (losowego) zysku inwestora
posiadającego dany portfel akcji do kwoty (znanej, nielosowej)
zainwestowanej w ten portfel na początku; jest to więc zmienna
losowa
Zatem wartość oczekiwana stopy zwrotu z portfela ![]() ,
oznaczana teraz i w dalszych wykładach
,
oznaczana teraz i w dalszych wykładach ![]() , wynosi
, wynosi
Natomiast wariancję stopy zwrotu z portfela ![]() , oznaczaną teraz
i w dalszych wykładach
, oznaczaną teraz
i w dalszych wykładach ![]() , liczymy trochę spokojniej
, liczymy trochę spokojniej
Jest to forma kwadratowa od ![]() . Jej współczynniki mają w
analizie portfelowej (i też szerzej w rachunku prawdopodobieństwa)
swoje klasyczne oznaczenia
. Jej współczynniki mają w
analizie portfelowej (i też szerzej w rachunku prawdopodobieństwa)
swoje klasyczne oznaczenia
Przypominamy tutaj, że wielkości te tylko estymujemy, gdyż nie mamy
wiedzy, by poznać je dokładnie. Dla naszych danych w przykładzie
otrzymujemy wyniki, celowo nie rozróżniając już tu niżej między
estymatorami i prawdziwymi (de facto nieznanymi) wartościami:
![]() ,
, ![]() ,
, ![]() . Zatem dla wszystkich dopuszczalnych portfeli
. Zatem dla wszystkich dopuszczalnych portfeli ![]() wariancje ich stopy zwrotu opisane
są wzorem
wariancje ich stopy zwrotu opisane
są wzorem
Jeżeli zauważymy teraz, że w naszej sytuacji ![]() , to
wzór na wariancję portfela, trochę nadużywając oznaczeń po lewej
stronie, uprości się do postaci
, to
wzór na wariancję portfela, trochę nadużywając oznaczeń po lewej
stronie, uprości się do postaci
gdzie ![]() jest dowolną liczbą z przedziału
jest dowolną liczbą z przedziału ![]() . Widzimy
więc, że w ten sposób uzyskaliśmy prosty przepis, jak możemy
manipulować ryzykiem naszego portfela poprzez odpowiedni dobór
jego składników (czyli zakup akcji A i B w stosownej proporcji).
Powyższa funkcja przyjmuje swoje minimum (globalne) w punkcie
. Widzimy
więc, że w ten sposób uzyskaliśmy prosty przepis, jak możemy
manipulować ryzykiem naszego portfela poprzez odpowiedni dobór
jego składników (czyli zakup akcji A i B w stosownej proporcji).
Powyższa funkcja przyjmuje swoje minimum (globalne) w punkcie
![]() i wynosi ono
i wynosi ono
![]() .
Zatem gdybyśmy za około 65
.
Zatem gdybyśmy za około 65![]() posiadanych pieniędzy nabyli
akcje spółki A, zaś pozostałe 35
posiadanych pieniędzy nabyli
akcje spółki A, zaś pozostałe 35![]() przeznaczyli na zakup
(kiepskich!) akcji spółki B, ryzyko naszego portfela (mierzone
odchyleniem standardowym jego stopy zwrotu) byłoby najmniejsze z
możliwych i wyniosłoby
przeznaczyli na zakup
(kiepskich!) akcji spółki B, ryzyko naszego portfela (mierzone
odchyleniem standardowym jego stopy zwrotu) byłoby najmniejsze z
możliwych i wyniosłoby ![]() , czyli około
16.30
, czyli około
16.30![]() ! Jest to o wiele mniej, niż 24.49
! Jest to o wiele mniej, niż 24.49![]() dla akcji spółki A,
czy 37.41
dla akcji spółki A,
czy 37.41![]() dla akcji spółki B. (Proszę spojrzeć w tym momencie
na wykres ilustrujący poprzedni przykład!) Niech nam się jednak
nie wydaje, że dokonaliśmy jakiegoś cudu — owszem, przy pomocy
,,kiepskich” akcji udało się znacznie zmniejszyć ryzyko, jednak
kosztem stopy zwrotu! Obliczmy oczekiwaną stopę zwrotu z takiego
portfela:
dla akcji spółki B. (Proszę spojrzeć w tym momencie
na wykres ilustrujący poprzedni przykład!) Niech nam się jednak
nie wydaje, że dokonaliśmy jakiegoś cudu — owszem, przy pomocy
,,kiepskich” akcji udało się znacznie zmniejszyć ryzyko, jednak
kosztem stopy zwrotu! Obliczmy oczekiwaną stopę zwrotu z takiego
portfela: ![]() . Jest to niestety mniej niż 25
. Jest to niestety mniej niż 25![]() możliwe do
uzyskania z inwestycji wyłącznie w ,,lepsze” akcje. Znowu więc
powraca pytanie, co wybrać: wyższy zwrot ale i wyższe ryzyko, czy
też zwrot niższy, ale przy niższym poziomie ryzyka? Narzędziem,
pomagającym w tego rodzaju dylematach okazuje się (najczęściej,
nie jedynie) tzw. wskaźnik, lub współczynnik Sharpe'a danego
portfela. W tych wykładach jest on systematycznie badany o
wiele później, poczynając od Wykładu IX (patrz w szczególności
Uwaga 9.1 w tamtym wykładzie).
możliwe do
uzyskania z inwestycji wyłącznie w ,,lepsze” akcje. Znowu więc
powraca pytanie, co wybrać: wyższy zwrot ale i wyższe ryzyko, czy
też zwrot niższy, ale przy niższym poziomie ryzyka? Narzędziem,
pomagającym w tego rodzaju dylematach okazuje się (najczęściej,
nie jedynie) tzw. wskaźnik, lub współczynnik Sharpe'a danego
portfela. W tych wykładach jest on systematycznie badany o
wiele później, poczynając od Wykładu IX (patrz w szczególności
Uwaga 9.1 w tamtym wykładzie).
Definiuje się go jako stosunek tzw. premii za ryzyko (mierzonej
różnicą między stopą zwrotu z inwestycji w portfel akcji i stopą
zwrotu pozbawioną ryzyka ![]() — związaną z nabywaniem bonów
skarbowych, obligacji, itp., czyli papierów wartościowych, z
których mamy zagwarantowany konkretny dochód) do ryzyka
(mierzonego odchyleniem standardowym stopy zwrotu
portfela). Formalnie, dla danego portfela
— związaną z nabywaniem bonów
skarbowych, obligacji, itp., czyli papierów wartościowych, z
których mamy zagwarantowany konkretny dochód) do ryzyka
(mierzonego odchyleniem standardowym stopy zwrotu
portfela). Formalnie, dla danego portfela ![]() ,
,
| (1.1) |
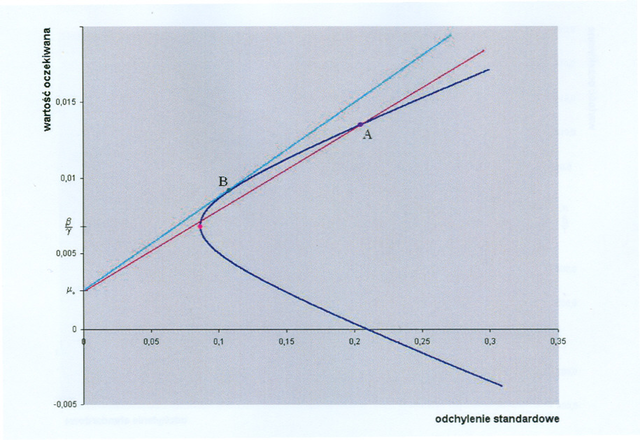
Można więc powiedzieć, że współczynnik Sharpe'a jest to względna premia za podjęcie ryzyka inwestycji w akcje. Zauważmy, że gdyby ryzyka portfeli były takie same, to większy współczynnik Sharpe'a oznaczałby wyższą stopę zwrotu. I podobnie, gdyby stopy zwrotu portfeli były równe, większy współczynnik Sharpe'a oznaczałby mniejsze ryzyko. Widzimy więc, jak naturalna jest przesłanka, by inwestorzy wybierali portfele, mające możliwie największy wskaźnik Sharpe'a. Niech za ilustrację tego służy następujący poglądowy rysunek,
na którym na pionowej osi widać punkt odniesienia – stopę
bezryzykowną ![]() i gdzie od razu widzimy, że portfel, którego
obrazem Markowitza jest punkt B, ma większy
wskaźnik Sharpe'a niż np portfel, którego obrazem jest punkt
A. Czy ten pierwszy (dający punkt B) nie ma
przypadkiem największego możliwego, w jakiejś niesprecyzowanej
jeszcze klasie portfeli, współczynnika Sharpe'a?
i gdzie od razu widzimy, że portfel, którego
obrazem Markowitza jest punkt B, ma większy
wskaźnik Sharpe'a niż np portfel, którego obrazem jest punkt
A. Czy ten pierwszy (dający punkt B) nie ma
przypadkiem największego możliwego, w jakiejś niesprecyzowanej
jeszcze klasie portfeli, współczynnika Sharpe'a?
(Obraz Markowitza danego portfela – podstawowe pojęcie w teorii
Markowitza – to punkt na płaszczyźnie ![]() mający
współrzędne: odchylenie standardowe i wartość oczekiwana tego
portfela. Będziemy systematycznie używać tego pojęcia już od
Wykładu II. Czy czytelnik, odczytując optycznie dane z Rysunku 1.3,
jest w stanie policzyć, według wzoru (1.1), przybliżone
wartości wskaźników Sharpe'a tych portfeli, których obrazami
Markowitza są punkty A i B ?)
mający
współrzędne: odchylenie standardowe i wartość oczekiwana tego
portfela. Będziemy systematycznie używać tego pojęcia już od
Wykładu II. Czy czytelnik, odczytując optycznie dane z Rysunku 1.3,
jest w stanie policzyć, według wzoru (1.1), przybliżone
wartości wskaźników Sharpe'a tych portfeli, których obrazami
Markowitza są punkty A i B ?)
Wracamy teraz do drugiego głównego przykładu dyskutowanego w tym wykładzie.
Przyjmijmy (w nim), że obecnie ![]() . Wtedy dla inwestycji w akcje
spółki A wskaźnik Sharpe'a wynosi
. Wtedy dla inwestycji w akcje
spółki A wskaźnik Sharpe'a wynosi ![]() .
Natomiast dla naszego portfela
.
Natomiast dla naszego portfela ![]() o minimalnym ryzyku mamy
o minimalnym ryzyku mamy ![]() . Jest to wynik
zdecydowanie słabszy!
. Jest to wynik
zdecydowanie słabszy!
Pozostaje jednak pytanie: czy jeżeli chcielibyśmy znaleźć portfel,
dla którego współczynnik Sharpe'a przyjmuje wartość największą
z możliwych (porównaj też Rysunek 1.3 powyżej), to czy właściwą
odpowiedzią będzie ten złożony tylko z akcji ,,najlepszej” spółki?
Otóż niekoniecznie! Często istnieje portfel ,,lepszy” i od portfela
dającego najwyższą stopę zwrotu i od portfela o minimalnym ryzyku.
Portfel taki ma wtedy stopę zwrotu znajdującą się pomiędzy stopami
zwrotu powyższych dwóch portfeli i nazywa się go portfelem
optymalnym ze względu na daną stopę zwrotu pozbawioną ryzyka.
Okazuje się, że w tym przykładzie jest to ![]() . I rzeczywiście, jego
wskaźnik Sharpe'a wynosi około 0.818, odrobinę lepiej, niż dla
portfela zawierającego wyłącznie akcje ,,najlepszej” spółki!
W późniejszych wykładach, poczynając od dziewiątego, poznamy
teorię dającą sposoby dochodzenia do takiego wyniku przy dwu
lub też większej (dowolnej) ilości spółek w modelu.
. I rzeczywiście, jego
wskaźnik Sharpe'a wynosi około 0.818, odrobinę lepiej, niż dla
portfela zawierającego wyłącznie akcje ,,najlepszej” spółki!
W późniejszych wykładach, poczynając od dziewiątego, poznamy
teorię dającą sposoby dochodzenia do takiego wyniku przy dwu
lub też większej (dowolnej) ilości spółek w modelu.