5. Wykład V, 30.X.2009
W Przykładach 4.1 i 4.2 w Wykładzie IV (w których ilość
spółek była jednakowa i równa 3) zbiory punktów [albo portfeli w pewnym
ogólniejszym sensie niż u Markowitza, który poznamy już w tym wykładzie]
krytycznych okazują się być prostymi. Czy tak jest tylko w wymiarze
![]() ? Od czego to zależy? Przyjmijmy już bez zwłoki ogólną
? Od czego to zależy? Przyjmijmy już bez zwłoki ogólną
Definicja 5.1
Dla dowolnego ustalonego ![]() , punkty krytyczne w analizie
portfelowej to punkty krytyczne, w sensie analizy matematycznej II,
zmodyfikowanego odwzorowania Markowitza
, punkty krytyczne w analizie
portfelowej to punkty krytyczne, w sensie analizy matematycznej II,
zmodyfikowanego odwzorowania Markowitza ![]() , tj takie punkty
, tj takie punkty ![]() ,
w których
,
w których ![]() .
.
(Patrz też uwagi przy pierwszym pojawieniu się tego pojęcia w Wykładzie IV. Markowitz do scharakteryzowania krytyczności portfela używał trochę innych słów, lecz miał na myśli to, co w tej definicji. Trochę nie zachowując proporcji, przypomnijmy dla porównania, że Leibniz przez dłuższy czas swój drugi rachunek nazywał calculus summatorius. Później Jakob I Bernoulli wprowadził słowo integral – i Leibniz to przyjął. Dalej używał już nazwy calculus integralis.)
Uwaga 5.1
(i) Przy ![]() każdy punkt z
każdy punkt z ![]() jest krytyczny w sensie podanej
tu definicji (bo wtedy
jest krytyczny w sensie podanej
tu definicji (bo wtedy ![]() jest 1-wymiarowa – jest prostą).
jest 1-wymiarowa – jest prostą).
(ii) W tej definicji, w zakresie punktów (portfeli uogólnionych) ![]() takich, że
takich, że ![]() , zamiast
, zamiast ![]() równoważnie można używać odwzorowania Markowitza
równoważnie można używać odwzorowania Markowitza ![]() . Istotnie, pomocnicze odwzorowanie
. Istotnie, pomocnicze odwzorowanie
![]() , gdzie zawsze
, gdzie zawsze ![]() ,
jest dyfeomorfizmem prawej półpłaszczyzny (
,
jest dyfeomorfizmem prawej półpłaszczyzny (![]() ) w
) w
![]() na prawą półpłaszczyznę (
na prawą półpłaszczyznę (![]() ) w
) w
![]() .
.
Będziemy niedługo szczegółowo badać, powtarzając zresztą rozumowanie kilku noblistów z dziedziny ekonomii, czym ogólnie w analizie portfelowej może być zbiór punktów krytycznych. Wcześniej chcemy jednak zebrać więcej materiału doświadczalnego nt krytyczności punktów. W pierwszej kolejności idzie
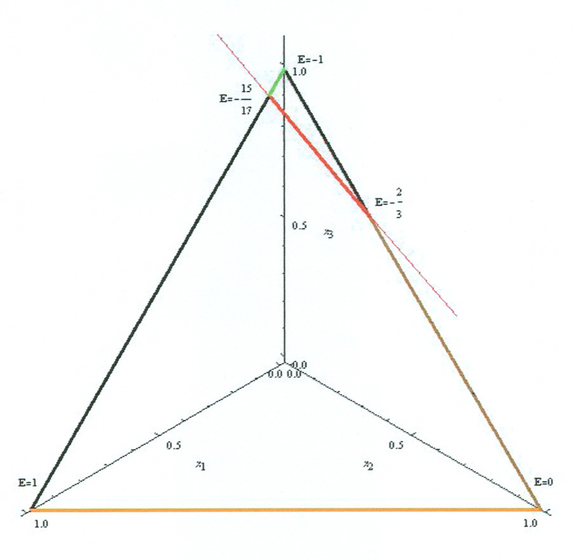
Przykład 5.1 (klasyczny, z wykładów [13])
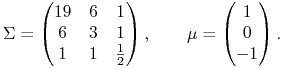 |
Chwilowo liczymy tu tylko obrazy boków, mając już zresztą do wyboru
dwie metody. Albo podstawienie do wzoru (3.2) z Wykładu III, albo
też jak w Przykładzie 4.2, np dla boku ![]() :
:
co wstawiamy do formy kwadratowej wariancji:
Tak dostajemy ![]() -obraz prostej zawierającej
bok
-obraz prostej zawierającej
bok ![]() : jest to parabola
: jest to parabola ![]() .
Analogicznie licząc, dostajemy
.
Analogicznie licząc, dostajemy
Co z punktami krytycznymi w tym modelu? Czy także tutaj ich
zbiór tworzy prostą? I jaki jest obraz tego zbioru? W przyszłości
odpowiedzi na takie pytania będą automatyczne; tu podajemy je
wprost. Odpowiedź na pytanie pierwsze jest twierdząca. Oto ta
prosta, tylko lekko zahaczająca sympleks standardowy ![]() :
:
Przykład ten, bardzo ważny, będzie jeszcze rozbudowywany (łącznie z dyskusją obrazów boków sympleksu i prostej krytycznej) w dalszych wykładach. Tymczasem bogactwo geometrycznych możliwości pokazuje
Przykład 5.2
Oto 1-parametrowa rodzina przykładów wychodzących od oryginalnego pomysłu studenta (Ł. Mordon) zgłoszonego jeszcze w roku akademickim 2007/08
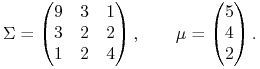 |
(5.1) |
Tę właśnie macierz ![]() zanurzamy w 1-parametrową rodzinę
macierzy
zanurzamy w 1-parametrową rodzinę
macierzy
 |
Przy ![]() mamy tu wyjściowy model
(5.1), zaś następnie nasz parametr
mamy tu wyjściowy model
(5.1), zaś następnie nasz parametr ![]() maleje
od
maleje
od ![]() do 0. (Wszystkie tak uzyskiwane
do 0. (Wszystkie tak uzyskiwane ![]() są dodatnio określone.4Jest dobrym ćwiczeniem znaleźć
wszystkie w ogóle
są dodatnio określone.4Jest dobrym ćwiczeniem znaleźć
wszystkie w ogóle ![]() , dla których
, dla których
![]() .)
.)
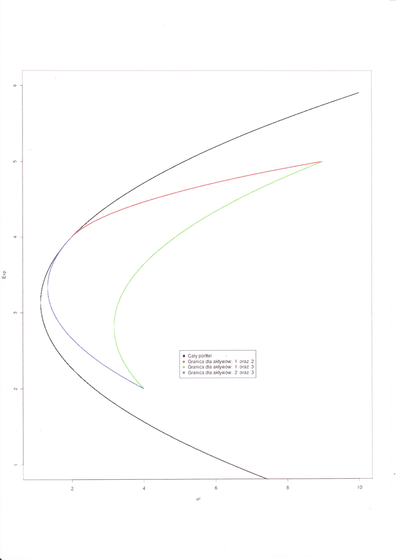
Okazuje się, że zbiory punktów krytycznych znowu zawsze są
tu prostymi! Przy tym ewoluują one w dość ciekawy sposób.
Oto ta ewolucja; autor: A. Zalewska (przypominamy, że
zbiory punktów krytycznych w analizie portfelowej są
podzbiorami płaszczyzny ![]() ).
).
Jak ta ewolucja prostych w płaszczyźnie ![]() odwzorowuje się
na płaszczyznę obrazu? To jest, jak to wygląda po obłożeniu
[bardziej graficznie poglądowym niż
odwzorowuje się
na płaszczyznę obrazu? To jest, jak to wygląda po obłożeniu
[bardziej graficznie poglądowym niż ![]() ] odwzorowaniem
] odwzorowaniem
![]() ? Autorem także jest A. Zalewska.
? Autorem także jest A. Zalewska.
Uwaga 5.2
Sam koniec (czy też początek) tego swoistego tańca parabol przedstawionego na drugim ,,filmie” powyżej, można też zobaczyć na rysunku wykonanym przez studenta WNE UW [w wersji pdf ten rysunek przeskoczył na następną stronę]:
Jeśli chodzi o drugi (przeciwny) koniec tej ewolucji parabol, to jest on pokazany na Rysunku 15.3 aż w Wykładzie XV (służy tam ilustracji zupełnie innych zjawisk, niż poruszane tutaj) i jest również widoczny na drugim filmiku powyżej.
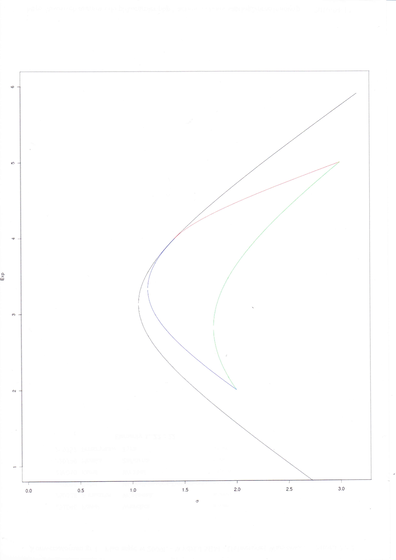
Ktoś może powiedzieć, że Rysunek 5.2 jest mało kanoniczny
– nie jest przecież na płaszczyźnie ![]() . Oto, jak
wygląda on całkiem kanonicznie, tj po obłożeniu znanym i wspominanym
już w tych wykładach dyfeomorfizmem5jakim ? przenoszącym
parabole na hiperbole (prawa autorskie należą tu do tego samego
co poprzednio studenta WNE UW) [w wersji pdf Rysunek 5.3 jest
dopiero dwie strony dalej]:
. Oto, jak
wygląda on całkiem kanonicznie, tj po obłożeniu znanym i wspominanym
już w tych wykładach dyfeomorfizmem5jakim ? przenoszącym
parabole na hiperbole (prawa autorskie należą tu do tego samego
co poprzednio studenta WNE UW) [w wersji pdf Rysunek 5.3 jest
dopiero dwie strony dalej]:
Należy wspomnieć, że sytuacja pokazana na Rysunkach 5.2 i 5.3
– przyklejanie się obrazu sympleksu standardowego do pocisku
Markowitza tylko w jednym punkcie położonym w górnej
połowie pocisku (dla ![]() ) – była postulowana i poszukiwana
przez szereg lat trwania wykładów z APRK1 na Wydziale MIM UW.
Przełom przyniosło dopiero w roku akademickim 2007/08 uzmiennienie
współczynnika
) – była postulowana i poszukiwana
przez szereg lat trwania wykładów z APRK1 na Wydziale MIM UW.
Przełom przyniosło dopiero w roku akademickim 2007/08 uzmiennienie
współczynnika ![]() w przykładzie Mordona (Przykład 5.2
powyżej), które nie byłoby możliwe bez samego tego przykładu!
w przykładzie Mordona (Przykład 5.2
powyżej), które nie byłoby możliwe bez samego tego przykładu!
Ćwiczenie 5.1 (trudniejsze)
Znaleźć wartość(ci) ![]() , przy której(ych)
prosta krytyczna jest tu równoległa do boku
, przy której(ych)
prosta krytyczna jest tu równoległa do boku ![]() .
Jaką współrzędną
.
Jaką współrzędną ![]() mają wtedy punkty (portfele uogólnione)
krytyczne w analizie portfelowej? Czy wtedy obraz
boku
mają wtedy punkty (portfele uogólnione)
krytyczne w analizie portfelowej? Czy wtedy obraz
boku ![]() jest przesunięciem obrazu
prostej krytycznej, a jeśli tak, to o jaki wektor? (Cały czas
rozważamy tu zmodyfikowane odwzorowanie Markowitza.)
jest przesunięciem obrazu
prostej krytycznej, a jeśli tak, to o jaki wektor? (Cały czas
rozważamy tu zmodyfikowane odwzorowanie Markowitza.)
Ćwiczenie 5.2 (łatwiejsze, lecz wcale nie natychmiastowe)
Znaleźć wszystkie punkty krytyczne w analizie portfelowej nad modelem Markowitza doskonale dodatnio skorelowanym.
Znaleźć wszystkie punkty krytyczne w analizie portfelowej
nad modelem Markowitza doskonale ![]() skorelowanym.
skorelowanym.
Przy ![]() odpowiedzi silnie zależą od wzajemnego położenia
punktów
odpowiedzi silnie zależą od wzajemnego położenia
punktów ![]() ,
, ![]() ,
na płaszczyźnie
,
na płaszczyźnie ![]() .
.
W dojściu do odpowiedzi pomocny może też być jeden z obrazów sympleksów standardowych (który?) na Rysunku 3.1 w Wykładzie III.
W dalszym ciągu6i już do końca w tych wykładach; czasem będziemy nawet zakładać więcej zakładamy, że
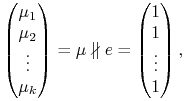 |
tzn., że nie wszystkie wartości oczekiwane ![]() stóp zwrotu
stóp zwrotu
![]() (
(![]() ) są równe. Będziemy to krótko
notować jak już tu wyżej:
) są równe. Będziemy to krótko
notować jak już tu wyżej:
| (5.2) |
Skoro proste krytyczne (czy ogólniej: zbiory punktów krytycznych
w analizie portfelowej) są tak ważne, to jak bardziej operatywnie
sprawdzać, czy punkt ![]() (czy też
(czy też ![]() ) jest
krytyczny w analizie portfelowej? Innymi słowy, jak sprawdzać, czy
odwzorowanie
) jest
krytyczny w analizie portfelowej? Innymi słowy, jak sprawdzać, czy
odwzorowanie ![]() jest krytyczne w
jest krytyczne w ![]() .
.
Twierdzenie 5.1
Przy bardzo ogólnych założeniach ![]() i
i ![]() ,
punkt
,
punkt ![]() jest krytyczny w sensie analizy portfelowej
jest krytyczny w sensie analizy portfelowej
![]()
![]() .
.
To twierdzenie pojawiało się w pierwszych wersjach wykładów [13], zaś później – w szczególności w wersji z roku 2000 – już tylko jako zadanie z gwiazdką.7Cóż to były za czasy! Obecnie jego zwarty dowód dany tu niżej jest za długi do wyłożenia w realnym czasie wykładu. Przy tym zadanie z gwiazdką dotyczyło równoważności spojrzenia Markowitza (relatywna minimalizacja ryzyka, ale w aspekcie B) i Definicji 5.1; Twierdzenie 5.1 w takiej operatywnej postaci jw w ogóle tam nie występowało. To pokazuje przy okazji całkiem odmienne filozofie wykładów Krzyżewskiego i tu prezentowanych: w bieżących to twierdzenie jest zupełnie podstawowym narzędziem. Jeśli zaś chodzi o gwiazdkę przy zadaniu w [13], to mniej więcej obejmuje ona dowód Twierdzenia 5.1.
Przykład 5.3 (Przykład działania tego twierdzenia (jeszcze przed jego dowodem))
Zwracamy uwagę, że wymiar w przykładzie jest 3 i założenie (5.2) jest spełnione, więc sprawdzenie założenia `rząd 2' w twierdzeniu to sprawdzenie zachodzenia jednego równania.
Mianowicie punkt (portfel Markowitza) ![]() jest krytyczny w
jest krytyczny w ![]() wziętym
z Przykładu 5.2:
wziętym
z Przykładu 5.2:
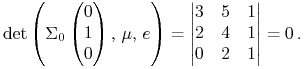 |
Portfel Markowitza ![]() jest krytyczny w modelu
jest krytyczny w modelu
![]() też
wziętym z Przykładu 5.2:
też
wziętym z Przykładu 5.2:
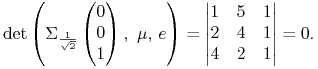 |
Dowód twierdzenia.
Na potrzeby tego dowodu piszemy Var zamiast ![]() , przy czym
Var
, przy czym
Var![]() dla wszystkich
dla wszystkich ![]() ,
nie tylko
,
nie tylko ![]() .
.
![]() Przechodząc od gradientów do pochodnych
(czyli pewnych 1-form różniczkowych), założenie, które mamy
przy dowodzeniu implikacji w tę stronę zapisujemy w postaci
Przechodząc od gradientów do pochodnych
(czyli pewnych 1-form różniczkowych), założenie, które mamy
przy dowodzeniu implikacji w tę stronę zapisujemy w postaci
po czym przeciągamy wszystkie występujące tu 1-formy wstecz
(pull-back) przy pomocy ![]() , gdzie
, gdzie
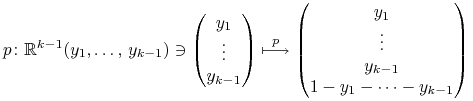 |
to parametryzacja hiperpłaszczyzny ![]() przy pomocy
przy pomocy
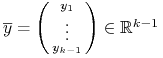 , w szczególności
, w szczególności
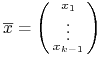 ,
, ![]() :
:
Ponieważ ![]() (patrz np Tw. 4.10 (4) w [28]),
zaś pull-back funkcji (tj 0-form) to po prostu składanie
funkcji z przeciągającym przekształceniem (tu
(patrz np Tw. 4.10 (4) w [28]),
zaś pull-back funkcji (tj 0-form) to po prostu składanie
funkcji z przeciągającym przekształceniem (tu ![]() ), więc
), więc
Lecz ![]() , więc
, więc
![]() .
Zatem
.
Zatem
tzn. pochodne w ![]() pierwszej i drugiej składowej
odwzorowania
pierwszej i drugiej składowej
odwzorowania ![]() są proporcjonalne
(pierwsza jest wielokrotnością drugiej). Pokazaliśmy, że
są proporcjonalne
(pierwsza jest wielokrotnością drugiej). Pokazaliśmy, że ![]() .
.
![]() Ponieważ
Ponieważ
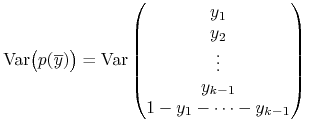 |
oraz
więc krytyczność punktu ![]() oznacza, że
oznacza, że
przy czym drugi wiersz tej macierzy jest niezerowy,
bo ![]() .
.
Zatem pierwszy wiersz jest pewną wielokrotnością drugiego
wiersza. W (czytelniejszym) zapisie kolumnowym
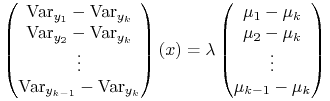 |
przy pewnym ![]() . Zapiszmy tę równość
tylko pozornie inaczej, sztucznie wydłużając o jedno
zero wektory występujące po obu stronach:
. Zapiszmy tę równość
tylko pozornie inaczej, sztucznie wydłużając o jedno
zero wektory występujące po obu stronach:
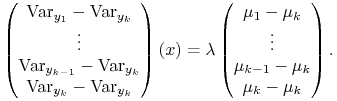 |
Dostaliśmy w ten sposób
co daje potrzebne wyrażenie dla ![]() ze współczynnikami
ze współczynnikami
![]() ,
, ![]() .
.
Ćwiczenie 5.3 (pytanie kontrolne po dowodzie twierdzenia)
Jakie ograniczenie(a) na zbiór punktów krytycznych w [danym modelu w] analizie portfelowej nakłada to twierdzenie (czym, ogólnie rzecz biorąc, jest/może być taki zbiór)?
W tej chwili mamy już dwa opisy krytyczności punktów z ![]() (nie
tylko klasycznych portfeli Markowitza z
(nie
tylko klasycznych portfeli Markowitza z ![]() !):
definicyjny i dany poprzez to dopiero co udowodnione twierdzenie.
Jest najwyższa pora wyjaśnić, co dla nas znaczą wszystkie
punkty
!):
definicyjny i dany poprzez to dopiero co udowodnione twierdzenie.
Jest najwyższa pora wyjaśnić, co dla nas znaczą wszystkie
punkty ![]() , tj takie
, tj takie ![]() , że
, że ![]() , spośród których tylko nieliczne
są, przy ustalonych parametrach modelu, krytyczne.
, spośród których tylko nieliczne
są, przy ustalonych parametrach modelu, krytyczne.
Odpowiedź będzie modelowaniem tzw. nieograniczonej krótkiej sprzedaży (ang. unrestricted short selling) wg podejścia Blacka i współautorów z wczesnych lat 1970ch – porównaj szczególnie strony 11 oraz 39 w [22].
Portfel inwestora w modelu Blacka, a więc – powtarzamy – z dopuszczalną nieograniczoną krótką sprzedażą
-
Inwestor wkracza do Domu Maklerskiego (dalej DM) z kwotą
 (np złotych czy funtów).
(np złotych czy funtów).
-
Po okazaniu kwoty
 , pożycza w DM według swojego uznania
akcje spółek o numerach
, pożycza w DM według swojego uznania
akcje spółek o numerach 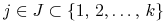 .
Konkretnie, tyle akcji spółki
.
Konkretnie, tyle akcji spółki 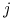 -tej, że (albo: by) ich obecna
wartość jest (była)
-tej, że (albo: by) ich obecna
wartość jest (była) 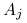 , dla
, dla 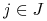 .
.
-
Pożyczone akcje spółek o numerach
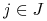 natychmiast,
tego samego dnia, sprzedaje na giełdzie. W wyniku tego ma teraz
natychmiast,
tego samego dnia, sprzedaje na giełdzie. W wyniku tego ma teraz
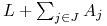 złotych (czy funtów,
złotych (czy funtów, 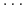 ).
).
-
Za wszystkie te środki od razu kupuje akcje spółek o numerach
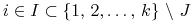 .
Konkretnie, tyle akcji spółki
.
Konkretnie, tyle akcji spółki 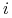 -tej, że (albo: by) ich
obecna wartość jest (była)
-tej, że (albo: by) ich
obecna wartość jest (była) 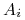 ,
, 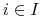 , przy czym,
oczywiście,
, przy czym,
oczywiście,
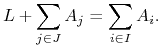
(5.3)
Można się już domyślać, jaka będzie dalsza strategia inwestora
– od tego zaczniemy następny wykład. W tej chwili chcemy
`tylko' matematycznie zakodować opisaną działalność inwestora.
W tym celu zapisujemy równość bilansową (5.3) trochę
inaczej
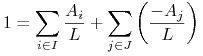 |
(5.4) |
i oznaczamy ![]() dla
dla ![]() , oraz
, oraz
![]() dla
dla ![]() . Dla indeksów
. Dla indeksów
![]() kładziemy
kładziemy
![]() . Portfel inwestora jest teraz zakodowany jako wektor
. Portfel inwestora jest teraz zakodowany jako wektor
![]() .
Mamy, dzięki (5.4),
.
Mamy, dzięki (5.4), ![]() . Mówimy, że w spółkach o
numerach
. Mówimy, że w spółkach o
numerach ![]() inwestor zajął długie pozycje (jest to zakodowane
poprzez dodatni znak
inwestor zajął długie pozycje (jest to zakodowane
poprzez dodatni znak ![]() :
: ![]() ), zaś w spółkach o numerach
), zaś w spółkach o numerach
![]() zajął krótkie pozycje (zakodowane poprzez ujemny znak
zajął krótkie pozycje (zakodowane poprzez ujemny znak
![]() :
: ![]() ).
).
Ćwiczenie 5.4 (pytanie kontrolne)
Inwestor miał 4 tysiące zł kapitału własnego. Z krótkiej sprzedaży
akcji spółek C i D uzyskał odpowiednio 7 i 13 tysięcy zł. Następnie
kupił (czyli zajął długie pozycje w) akcje(ach) spółek A i B w
proporcji wartościowej ![]() . Wyznaczyć portfel tego inwestora
zapisany w modelu Blacka.
. Wyznaczyć portfel tego inwestora
zapisany w modelu Blacka.
![]() .
.
Dzięki informacji zawartej we wskazówce widzimy, że
portfelem inwestora jest ![]() .
.