Zagadnienia
4. Warunkowa wartość oczekiwana
Warunkowa wartość oczekiwana jest jednym z kluczowych pojęć w teorii prawdopodobieństwa. Zacznijmy od sytuacji gdy warunkujemy względem zdarzenia.
Definicja 4.1
Załóżmy, że ![]() jest przestrzenią
probabilistyczną oraz
jest przestrzenią
probabilistyczną oraz ![]() jest zdarzeniem o dodatnim
prawdopodobieństwie. Niech
jest zdarzeniem o dodatnim
prawdopodobieństwie. Niech ![]() będzie całkowalną zmienną losową.
Warunkową wartością oczekiwaną
będzie całkowalną zmienną losową.
Warunkową wartością oczekiwaną ![]() pod warunkiem
pod warunkiem ![]() nazywamy
liczbę
nazywamy
liczbę
Stwierdzenie 4.1
Przy założeniach jak wyżej,
| (*) |
Dowód:
Stosujemy standardową metodę komplikacji
zmiennej ![]() .
.
1. Załóżmy najpierw, że ![]() , gdzie
, gdzie ![]() . Wówczas
. Wówczas
2. Z liniowości, dowodzona równość zachodzi także dla zmiennych prostych (kombinacji liniowych indykatorów zdarzeń).
3. Teraz jeśli ![]() jest nieujemną zmienną losową, to bierzemy
niemalejący ciąg
jest nieujemną zmienną losową, to bierzemy
niemalejący ciąg ![]() zmiennych prostych zbieżny prawie na pewno
do
zmiennych prostych zbieżny prawie na pewno
do ![]() . Pisząc (*) dla
. Pisząc (*) dla ![]() i zbiegając z
i zbiegając z ![]() dostajemy (*)
dla
dostajemy (*)
dla ![]() , na mocy twierdzenia Lebesgue'a o monotonicznym przejściu do
granicy pod znakiem całki.
, na mocy twierdzenia Lebesgue'a o monotonicznym przejściu do
granicy pod znakiem całki.
4. Jeśli ![]() jest dowolną zmienną losową, to rozważamy rozbicie
jest dowolną zmienną losową, to rozważamy rozbicie
![]() i stosujemy (*) dla
i stosujemy (*) dla ![]() oraz
oraz ![]() ; po odjęciu stronami
dostajemy (*) dla
; po odjęciu stronami
dostajemy (*) dla ![]() .
.
Przechodzimy do definicji warunkowej wartości oczekiwanej względem
![]() -ciała.
-ciała.
Definicja 4.2
Załóżmy, że ![]() jest przestrzenią
probabilistyczną,
jest przestrzenią
probabilistyczną, ![]() jest pod-
jest pod-![]() -ciałem
-ciałem ![]() , a
, a ![]() jest całkowalną zmienną losową. Warunkową wartością oczekiwaną
jest całkowalną zmienną losową. Warunkową wartością oczekiwaną
![]() pod warunkiem
pod warunkiem ![]() nazywamy taką zmienną losową
nazywamy taką zmienną losową ![]() ,
że są spełnione następujące dwa warunki.
,
że są spełnione następujące dwa warunki.
1) ![]() jest mierzalna względem
jest mierzalna względem ![]() .
.
2) Dla każdego ![]() ,
,
Oznaczenie: ![]() .
.
W szczególności gdy ![]() ,
, ![]() , to definiujemy
prawdopodobieństwo warunkowe zdarzenia
, to definiujemy
prawdopodobieństwo warunkowe zdarzenia ![]() pod warunkiem
pod warunkiem ![]() poprzez
poprzez ![]()
Twierdzenie 4.1
Załóżmy, że ![]() jest całkowalną zmienną losową, a
jest całkowalną zmienną losową, a ![]() jest pod-
jest pod-![]() -ciałem
-ciałem ![]() . Wówczas warunkowa wartość oczekiwana
istnieje i jest wyznaczona jednoznacznie z dokładnością do
równości p.n.
. Wówczas warunkowa wartość oczekiwana
istnieje i jest wyznaczona jednoznacznie z dokładnością do
równości p.n.
Dowód:
Dla dowolnego ![]() definiujemy
definiujemy
![]() . Funkcja
. Funkcja ![]() jest
przeliczalnie addytywną funkcją zbioru. Ponadto jeśli
jest
przeliczalnie addytywną funkcją zbioru. Ponadto jeśli
![]() , to
, to ![]() (jest to tzw. absolutna ciągłość
(jest to tzw. absolutna ciągłość
![]() względem
względem ![]() ). Na mocy twierdzenia Radona-Nikodyma
istnieje
). Na mocy twierdzenia Radona-Nikodyma
istnieje ![]() -mierzalna zmienna losowa
-mierzalna zmienna losowa ![]() będąca
gęstością
będąca
gęstością ![]() względem
względem ![]() , tzn. taka, że dla wszystkich
, tzn. taka, że dla wszystkich
![]() ,
,
Jednoznaczność jest oczywista: jeśli ![]() ,
, ![]() są
zmiennymi losowymi spełniającymi 1) oraz 2), to w szczególności,
dla każdego
są
zmiennymi losowymi spełniającymi 1) oraz 2), to w szczególności,
dla każdego ![]() ,
,
![]() , skąd
, skąd
![]() p.n.
p.n.
Uwaga: Warto tu przyjrzeć się warunkowej wartości oczekiwanej zmiennej ![]() względem
względem ![]() -ciała
-ciała ![]() generowanego przez co najwyżej przeliczalne rozbicie
generowanego przez co najwyżej przeliczalne rozbicie ![]() zbiorów o dodatnim prawdopodobieństwie. Bardzo łatwo wyznaczyć tę
zmienną w oparciu o powyższą definicję. Mianowicie, jak widać z warunku 1),
zbiorów o dodatnim prawdopodobieństwie. Bardzo łatwo wyznaczyć tę
zmienną w oparciu o powyższą definicję. Mianowicie, jak widać z warunku 1), ![]() musi być stała na każdym zbiorze
musi być stała na każdym zbiorze ![]() ,
, ![]() ;
własność 2) natychmiast implikuje, iż
;
własność 2) natychmiast implikuje, iż ![]() na zbiorze
na zbiorze ![]() . To w jednoznaczny sposób opisuje warunkową wartość oczekiwaną.
. To w jednoznaczny sposób opisuje warunkową wartość oczekiwaną.
Przechodzimy do pojęcia warunkowej wartości oczekiwanej względem zmiennej losowej. Będziemy potrzebować następującego pomocniczego faktu.
Lemat 4.1
Załóżmy, że ![]() jest zmienną losową. Wówczas każda zmienna
losowa
jest zmienną losową. Wówczas każda zmienna
losowa ![]() mierzalna względem
mierzalna względem ![]() ma postać
ma postać ![]() dla pewnej
funkcji borelowskiej
dla pewnej
funkcji borelowskiej ![]() .
.
Dowód:
Ponownie stosujemy metodę komplikacji zmiennej.
1. Załóżmy, że ![]() , gdzie
, gdzie ![]() . Wówczas
. Wówczas ![]() dla pewnego
dla pewnego ![]() , skąd
, skąd ![]() , czyli jako
, czyli jako ![]() możemy wziąć
indykator
możemy wziąć
indykator ![]() .
.
2. Jeśli ![]() jest zmienną prostą, to jako
jest zmienną prostą, to jako ![]() bierzemy
kombinację liniową odpowiednich indykatorów (patrz poprzedni punkt).
bierzemy
kombinację liniową odpowiednich indykatorów (patrz poprzedni punkt).
3. Załóżmy, że ![]() jest nieujemną zmienną losową. Istnieje
niemalejący ciąg
jest nieujemną zmienną losową. Istnieje
niemalejący ciąg ![]() prostych,
prostych, ![]() -mierzalnych zmiennych
losowych zbieżny do
-mierzalnych zmiennych
losowych zbieżny do ![]() . Na mocy 2), mamy
. Na mocy 2), mamy ![]() dla pewnego
ciągu funkcyjnego
dla pewnego
ciągu funkcyjnego ![]() . Jak łatwo sprawdzić, wystarczy wziąć
. Jak łatwo sprawdzić, wystarczy wziąć
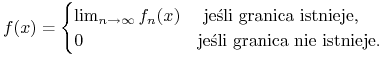 |
4. Jeśli teraz ![]() jest dowolną zmienną losową, to mamy
jest dowolną zmienną losową, to mamy
![]() , gdzie
, gdzie ![]() ,
, ![]() to funkcje
borelowskie odpowiadające
to funkcje
borelowskie odpowiadające ![]() -mierzalnym
-mierzalnym ![]() oraz
oraz ![]() .
.
Definicja 4.3
Załóżmy, że ![]() są zmiennymi losowymi, przy czym
są zmiennymi losowymi, przy czym ![]() jest
całkowalna. Definiujemy warunkową wartość oczekiwaną
jest
całkowalna. Definiujemy warunkową wartość oczekiwaną ![]() pod
warunkiem
pod
warunkiem ![]() jako
jako
Uwaga: Na mocy lematu mamy ![]() dla pewnej funkcji
borelowskiej
dla pewnej funkcji
borelowskiej ![]() . Liczbę
. Liczbę ![]() możemy interpretować jako
możemy interpretować jako
![]() .
.
Przykłady:
1. Załóżmy, że ![]() ,
, ![]() posiadają rozkłady skokowe. Oznaczmy
posiadają rozkłady skokowe. Oznaczmy
Jeśli ![]() jest dowolną funkcją borelowską taką, że
jest dowolną funkcją borelowską taką, że ![]() ,
to
,
to
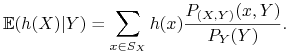 |
Aby to wykazać, należy sprawdzić, iż prawa strona (oznaczana dalej
przez ![]() ) spełnia własności 1) i 2) z definicji
) spełnia własności 1) i 2) z definicji
![]() . Pierwszy warunek jest jasny -
. Pierwszy warunek jest jasny - ![]() , jako funkcja
, jako funkcja
![]() , jest
, jest ![]() -mierzalna. Zajmijmy się zatem drugim warunkiem.
niech
-mierzalna. Zajmijmy się zatem drugim warunkiem.
niech ![]() . Ponieważ
. Ponieważ ![]() ma rozkład dyskretny,
ma rozkład dyskretny,
![]() jest co najwyżej przeliczalną sumą zdarzeń postaci
jest co najwyżej przeliczalną sumą zdarzeń postaci ![]() oraz zdarzenia o prawdopodobieństwie
oraz zdarzenia o prawdopodobieństwie ![]() . Wystarczy więc sprawdzić
2) dla zbiorów
. Wystarczy więc sprawdzić
2) dla zbiorów ![]() postaci
postaci ![]() . Mamy
. Mamy
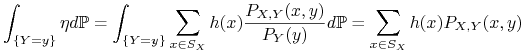 |
oraz
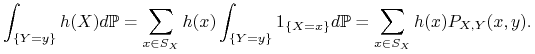 |
2. Konkretny przykład. Załóżmy, że ![]() ,
, ![]() są niezależnymi
zmiennymi losowymi o rozkładzie Poissona z parametrami
są niezależnymi
zmiennymi losowymi o rozkładzie Poissona z parametrami
![]() , odpowiednio. Wyznaczymy
, odpowiednio. Wyznaczymy ![]() .
.
Wiadomo, że ![]() ma rozkład Poissona z parametrem
ma rozkład Poissona z parametrem ![]() .
Stąd
.
Stąd
Ponadto, jeśli ![]() , to
, to
i
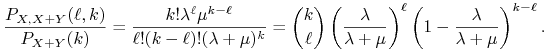 |
Stąd
3. Załóżmy, że ![]() ma rozkład z gęstością
ma rozkład z gęstością ![]() i niech
i niech
![]() będzie gęstością zmiennej
będzie gęstością zmiennej ![]() . Zdefiniujmy
gęstość warunkową wzorem
. Zdefiniujmy
gęstość warunkową wzorem
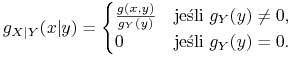 |
Wówczas dla dowolnej funkcji borelowskiej ![]() mamy
mamy
| (*) |
Istotnie, sprawdzimy, że prawa strona spełnia warunki 1) i 2) z
definicji ![]() . Oczywiście warunek 1) jest spełniony - prawa
strona jest funkcją od
. Oczywiście warunek 1) jest spełniony - prawa
strona jest funkcją od ![]() . Przejdźmy do 2). Dla dowolnego
. Przejdźmy do 2). Dla dowolnego
![]() mamy, iż
mamy, iż ![]() dla pewnego
dla pewnego ![]() oraz
oraz
Własności warunkowej wartości oczekiwanej
Załóżmy, że ![]() jest ustaloną przestrzenią
probabilistyczną i niech
jest ustaloną przestrzenią
probabilistyczną i niech ![]() będzie pewnym
pod-
będzie pewnym
pod-![]() -ciałem
-ciałem ![]() . Ponadto, o wszystkich zmiennych losowych
zakładamy, że są całkowalne.
. Ponadto, o wszystkich zmiennych losowych
zakładamy, że są całkowalne.
0. Mamy ![]() . Wynika to natychmiast z 2),
jeśli weźmiemy
. Wynika to natychmiast z 2),
jeśli weźmiemy ![]() .
.
1. Niech ![]() . Wówczas
. Wówczas
Istotnie: sprawdzimy, że prawa strona (oznaczana dalej przez ![]() ) spełnia warunki 1) i 2) z
definicji
) spełnia warunki 1) i 2) z
definicji ![]() . Pierwszy warunek jest
oczywisty. Aby sprawdzić drugi zauważmy, że dla dowolnego
. Pierwszy warunek jest
oczywisty. Aby sprawdzić drugi zauważmy, że dla dowolnego
![]() ,
,
2. Jeśli ![]() jest nieujemną zmienną losową, to
jest nieujemną zmienną losową, to
![]() p.n. Istotnie, niech
p.n. Istotnie, niech ![]() . Wówczas
. Wówczas ![]() i
i
Widzimy, że gdyby zdarzenie ![]() miało dodatnie prawdopodobieństwo,
to lewa strona byłaby ujemna, a prawa - nieujemna.
miało dodatnie prawdopodobieństwo,
to lewa strona byłaby ujemna, a prawa - nieujemna.
3. Mamy
| (*) |
Istotnie, na
mocy 1. oraz 2. mamy, iż nierówność ![]() p.n. pociąga za
sobą
p.n. pociąga za
sobą ![]() . Stąd, z
prawdopodobieństwem
. Stąd, z
prawdopodobieństwem ![]() ,
,
i
Biorąc wartość oczekiwaną obu stron w (*) dostajemy, na mocy 0.,
Innymi słowy, operator liniowy
![]() jest kontrakcją.
jest kontrakcją.
4. Warunkowa wersja twierdzenia Lebesgue'a o monotonicznym przejściu
do granicy. Załóżmy, że ![]() . Wówczas
. Wówczas
![]() p.n.
p.n.
Aby to wykazać, zacznijmy od obserwacji iż na mocy 1. i 2., ciąg
![]() jest z prawdopodobieństwem
jest z prawdopodobieństwem ![]() niemalejący, a
więc w szczególności zbieżny. Oznaczmy jego granicę przez
niemalejący, a
więc w szczególności zbieżny. Oznaczmy jego granicę przez ![]() ,
,
![]() . Niech teraz
. Niech teraz
![]() . Mamy, na mocy 2) oraz bezwarunkowego twierdzenia
Lebesgue'a,
. Mamy, na mocy 2) oraz bezwarunkowego twierdzenia
Lebesgue'a,
Ponieważ ![]() jest
jest ![]() -mierzalna, to z powyższej
równości wynika, iż
-mierzalna, to z powyższej
równości wynika, iż ![]() .
.
5. Analogicznie dowodzimy warunkowe wersje twierdzenia Lebesgue'a o zmajoryzowanym przejściu do granicy pod znakiem całki oraz lematu Fatou.
6. Załóżmy, że ![]() jest mierzalna względem
jest mierzalna względem ![]() oraz
oraz
![]() jest całkowalna. Wówczas
jest całkowalna. Wówczas
| (+) |
W szczególności, biorąc ![]() , dostajemy, iż
, dostajemy, iż
![]() .
.
Sprawdzamy, że prawa strona spełnia warunki 1) oraz 2) z definicji
![]() . Warunek 1) jest oczywisty, pozostaje więc
sprawdzić drugi. Zastosujemy metodę komplikacji zmiennej
. Warunek 1) jest oczywisty, pozostaje więc
sprawdzić drugi. Zastosujemy metodę komplikacji zmiennej
![]() .
.
a) Jeśli ![]() , gdzie
, gdzie ![]() , to dla dowolnego
, to dla dowolnego
![]() ,
,
b) Jeśli ![]() jest zmienną prostą, to wzór
jest zmienną prostą, to wzór ![]() dostajemy na mocy
a) oraz liniowości warunkowych wartości oczekiwanych.
dostajemy na mocy
a) oraz liniowości warunkowych wartości oczekiwanych.
c) Jeśli ![]() jest nieujemną zmienną losową, to istnieje
niemalejący ciąg
jest nieujemną zmienną losową, to istnieje
niemalejący ciąg ![]()
![]() -mierzalnych zmiennych prostych,
zbieżny p.n. do
-mierzalnych zmiennych prostych,
zbieżny p.n. do ![]() . Rozbijmy
. Rozbijmy ![]() i zastosujmy b) do
zmiennych
i zastosujmy b) do
zmiennych ![]() oraz
oraz ![]() :
:
Zbiegając z ![]() i korzystając z warunkowej wersji
twierdzenia Lebesgue'a (własność 4.), dostajemy
i korzystając z warunkowej wersji
twierdzenia Lebesgue'a (własność 4.), dostajemy
Zastępując ![]() przez
przez ![]() i powtarzając rozumowanie,
dostajemy
i powtarzając rozumowanie,
dostajemy
i po odjęciu stronami dostajemy (+).
d) Jeśli ![]() jest dowolną zmienną losową, to rozbijamy ją na
różnicę
jest dowolną zmienną losową, to rozbijamy ją na
różnicę ![]() , stoujemy c) do zmiennych
, stoujemy c) do zmiennych ![]() ,
, ![]() , oraz
, oraz
![]() ,
, ![]() , i odejmujemy stronami uzyskane równości.
, i odejmujemy stronami uzyskane równości.
7. Jeśli ![]() są
pod-
są
pod-![]() -ciałami
-ciałami ![]() , to
, to
| (=) |
Zacznijmy od obserwacji, iż wyrażenia stojące po skrajnych stronach
są równe. Wynika to natychmiast z poprzedniej własności:
zmienna losowa ![]() jest mierzalna względem
jest mierzalna względem
![]() . Wystarczy więc udowodnić, że pierwsze dwa wyrazy w
(=) są równe. Weźmy
. Wystarczy więc udowodnić, że pierwsze dwa wyrazy w
(=) są równe. Weźmy ![]() . Mamy
. Mamy ![]() , a więc
, a więc
skąd teza.
8. Załóżmy, że ![]() jest niezależna od
jest niezależna od ![]() . Wówczas
. Wówczas
![]() . Istotnie, sprawdzimy, że
. Istotnie, sprawdzimy, że ![]() spełnia
warunki 1) i 2) w definicji
spełnia
warunki 1) i 2) w definicji ![]() . Warunek 1) jest
oczywisty:
. Warunek 1) jest
oczywisty: ![]() jest zmienn:a losową stałą, a więc mierzalną
względem każdego
jest zmienn:a losową stałą, a więc mierzalną
względem każdego ![]() -ciała. Niech teraz
-ciała. Niech teraz ![]() . Mamy
na mocy niezależności
. Mamy
na mocy niezależności ![]() oraz
oraz ![]() ,
,
9. Nierówność Jensena. Załóżmy, że ![]() jest funkcją
wypukłą taką, że
jest funkcją
wypukłą taką, że ![]() jest zmienną całkowalną. Wówczas
jest zmienną całkowalną. Wówczas
Będzie nam potrzebny następujący prosty fakt. Dowód pozostawiamy jako proste ćwiczenie.
Lemat 4.2
Załóżmy, że ![]() jest funkcją wypukłą. Wówczas istnieją
ciągi
jest funkcją wypukłą. Wówczas istnieją
ciągi ![]() ,
, ![]() takie, że dla dowolnego
takie, że dla dowolnego ![]() ,
,
Powróćmy do dowodu 9. Dla ciągów ![]() ,
, ![]() , gwarantowanych
przez powyższy lemat, mamy
, gwarantowanych
przez powyższy lemat, mamy ![]() dla każdego
dla każdego ![]() .
Stąd, na mocy 1. oraz 2., z prawdopodobieństwem
.
Stąd, na mocy 1. oraz 2., z prawdopodobieństwem ![]() ,
,
Poniweaż ciągi ![]() ,
, ![]() są przeliczalne, to możemy wziąć
supremum po
są przeliczalne, to możemy wziąć
supremum po ![]() po prawej stronie i dalej nierówno'sć będzie
zachodziła z prawdopodobieństwem
po prawej stronie i dalej nierówno'sć będzie
zachodziła z prawdopodobieństwem ![]() :
:
Jako wniosek, dostajemy, iż dla ![]() i
i ![]() ,
,
Stąd po wzięciu wartości oczekiwanej obu stron,
![]() czyli
czyli
Zatem warunkowa wartość oczekiwana ![]() jest
kontrakcją w
jest
kontrakcją w ![]() .
.
4.1. Zadania
1. Załóżmy, że ![]() ,
, ![]() są zmiennymi losowymi a
są zmiennymi losowymi a ![]() jest
jest
![]() -ciałem takim, że
-ciałem takim, że ![]() jest mierzalne względem
jest mierzalne względem ![]() ,
a
,
a ![]() jest niezależne od
jest niezależne od ![]() . Niech
. Niech ![]() będzie funkcją borelowską taką, że
będzie funkcją borelowską taką, że ![]() jest całkowalną
zmienną losową. Udowodnić, że
jest całkowalną
zmienną losową. Udowodnić, że
gdzie ![]() .
.
2. Załóżmy, że ![]() jest całkowalną zmienną losową, a
jest całkowalną zmienną losową, a
![]() -ciało
-ciało ![]() jest niezależne od
jest niezależne od ![]() oraz od
oraz od
![]() -ciała
-ciała ![]() . Udowodnić, że
. Udowodnić, że
3. Zmienna losowa ![]() ma gęstość
ma gęstość
Wyznaczyć ![]() oraz
oraz ![]() .
.
4. Zmienna losowa ![]() ma rozkład Gaussa o wartości
oczekiwanej
ma rozkład Gaussa o wartości
oczekiwanej ![]() , Var
, Var![]() , Var
, Var![]() , Cov
, Cov![]() .
Obliczyć
.
Obliczyć ![]() (dla
(dla ![]() ) oraz
) oraz ![]() .
.
5. Zmienne losowe ![]() ,
, ![]() są niezależne i mają rozkład
wykładniczy z parametrem
są niezależne i mają rozkład
wykładniczy z parametrem ![]() . Obliczyć
. Obliczyć ![]() (dla
(dla ![]() ) oraz
) oraz ![]() .
.
6. Zmienne losowe ![]() są niezależne i mają
ten sam rozkład
są niezależne i mają
ten sam rozkład ![]() ,
,
![]() . Obliczyć
. Obliczyć ![]() oraz
oraz
![]() .
.
7. Wiadomo, że ![]() procent monet stanowią monety fałszywe,
z orłem po obu stronach. Losujemy ze zwracaniem
procent monet stanowią monety fałszywe,
z orłem po obu stronach. Losujemy ze zwracaniem ![]() monet i każdą z
nich wykonujemy rzut. Niech
monet i każdą z
nich wykonujemy rzut. Niech ![]() oznacza liczbę losowań, w wyniku
których wyciągnięto monetę fałszywą,
oznacza liczbę losowań, w wyniku
których wyciągnięto monetę fałszywą, ![]() - liczba wyrzuconych
orłów. Udowodnić, że
- liczba wyrzuconych
orłów. Udowodnić, że ![]()
8. Zmienna losowa ![]() ma rozkład wykładniczy z parametrem
ma rozkład wykładniczy z parametrem
![]() , zaś
, zaś ![]() jest zmienną losową taką, że jeśli
jest zmienną losową taką, że jeśli ![]() , to
, to ![]() ma
rozkład wykładniczy z parametrem
ma
rozkład wykładniczy z parametrem ![]() .
.
a) Wyznaczyć rozkład ![]() .
.
b) Obliczyć ![]() .
.
9. Losujemy ze zwracaniem po jednej karcie z talii ![]() kart tak
długo aż wyciągniemy pika. Niech
kart tak
długo aż wyciągniemy pika. Niech ![]() oznacza zmienną losową równą liczbie wyciągniętych kart,
a
oznacza zmienną losową równą liczbie wyciągniętych kart,
a ![]() zmienną losową równą liczbie wyciągniętych kierów. Wyznaczyć
zmienną losową równą liczbie wyciągniętych kierów. Wyznaczyć ![]() oraz
oraz ![]() .
.
10. Zmienne lsowe ![]() ,
, ![]() są niezależne i mają rozkład wykładniczy z parametrem
są niezależne i mają rozkład wykładniczy z parametrem ![]() . Obliczyć
. Obliczyć
![]() oraz
oraz ![]() .
.




