Zagadnienia
5. Martyngały z czasem dyskretnym
Do tej pory, dysponując ciągiem zmiennych losowych, nie
wiązaliśmy z ich indeksami żadnej interpretacji. W wielu naturalnych
sytuacjach można je interpretować jako współrzędną czasową. W
konkretnych przypadkach często ![]() opisuje zachowanie układu w chwili
opisuje zachowanie układu w chwili
![]() . Tak więc indeks odpowiada za czas.
. Tak więc indeks odpowiada za czas.
Załóżmy, że ![]() jest ,,zbiorem czasów”: to znaczy, jest równy
jest ,,zbiorem czasów”: to znaczy, jest równy
![]() ,
, ![]() ,
,
![]() lub
lub
![]() .
.
Definicja 5.1
Załóżmy, że ![]() jest przestrzenią
probabilistyczną,
jest przestrzenią
probabilistyczną, ![]() - jak wyżej. Filtracją nazywamy
rodzinę
- jak wyżej. Filtracją nazywamy
rodzinę ![]() , gdzie dla każdego
, gdzie dla każdego ![]() ,
, ![]() jest
jest
![]() -ciałem zawartym w
-ciałem zawartym w ![]() oraz
oraz ![]() jeśli
jeśli ![]() .
.
Intuicja: ![]() -ciało
-ciało ![]() opisuje wszystko co się może zdarzyć do
chwili
opisuje wszystko co się może zdarzyć do
chwili ![]() .
.
Definicja 5.2
Załóżmy, że ![]() jest przestrzenią
probabilistyczną wyposażoną w filtrację
jest przestrzenią
probabilistyczną wyposażoną w filtrację ![]() . Funkcję
. Funkcję
![]() nazywamy momentem zatrzymania,
jeśli dla każdego
nazywamy momentem zatrzymania,
jeśli dla każdego ![]() mamy
mamy ![]() .
.
Intuicyjnie, moment zatrzymania jest ,,sensowną” reguła stopowania:
taką, iż decyzję, czy się zatrzymywać, podejmujemy
na podstawie zdarzeń z przeszłości i teraźniejszości. Spójrzmy na
następujący
Przykład: Rzucamy ![]() razy monetą. Niech
razy monetą. Niech
![]() , jeśli w
, jeśli w ![]() -tym rzucie wypadł orzeł, i
-tym rzucie wypadł orzeł, i ![]() w przeciwnym
przypadku. Wprowadźmy
w przeciwnym
przypadku. Wprowadźmy ![]() -ciała
-ciała ![]() ,
,
![]() (jest to tzw. naturalna filtracja
względem ciągu
(jest to tzw. naturalna filtracja
względem ciągu ![]() ) Rozważmy dwie strategie:
) Rozważmy dwie strategie: ![]() - wycofujemy się, gdy
wypadnie orzeł po raz pierwszy,
- wycofujemy się, gdy
wypadnie orzeł po raz pierwszy, ![]() - wycofujemy się, gdy orzeł
wypada po raz ostatni (jeśli wypadają same reszki, przyjmujemy
- wycofujemy się, gdy orzeł
wypada po raz ostatni (jeśli wypadają same reszki, przyjmujemy
![]() ). Intuicja podpowiada, iż
). Intuicja podpowiada, iż ![]() jest sensowną
regułą zatrzymania - decyzję o tym, czy się wycofać, czy nie,
podejmujemy na podstawie informacji, które dopłynęły do nas do
danej chwili. Strategia
jest sensowną
regułą zatrzymania - decyzję o tym, czy się wycofać, czy nie,
podejmujemy na podstawie informacji, które dopłynęły do nas do
danej chwili. Strategia ![]() nie jest sensowna: skąd mamy
wiedzieć - nie znając przyszłości - czy orzeł, który właśnie
wypadł, jest ostatni? Formalny dowód tego, że
nie jest sensowna: skąd mamy
wiedzieć - nie znając przyszłości - czy orzeł, który właśnie
wypadł, jest ostatni? Formalny dowód tego, że ![]() nie jest
momentem zatrzymania, pozostawiamy jako ćwiczenie.
nie jest
momentem zatrzymania, pozostawiamy jako ćwiczenie.
Uwaga:
Warunek definiujący moment stopu można zapisać równoważnie w
następujący sposób. Funkcja ![]() jest momentem
zatrzymania wtedy i tylko wtedy, gdy dla każdego
jest momentem
zatrzymania wtedy i tylko wtedy, gdy dla każdego ![]() ,
, ![]() .
.
Dowód
![]() Mamy
Mamy
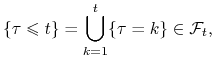 |
gdyż dla każdego ![]() ,
, ![]() .
.
![]() Mamy
Mamy ![]() i oba zdarzenia należą do
i oba zdarzenia należą do ![]() .
.
Przykłady:
1) ![]() jest momentem zatrzymania względem każdej
filtracji:
jest momentem zatrzymania względem każdej
filtracji:
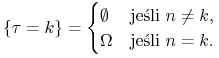 |
2) Załóżmy, że ![]() jest przestrzenią
probabilistyczną wyposażoną w filtrację
jest przestrzenią
probabilistyczną wyposażoną w filtrację ![]() .
Załóżmy, że
.
Załóżmy, że ![]() jest rodziną zmiennych losowych
(procesem stochastycznym) o tej własności, że dla każdego
jest rodziną zmiennych losowych
(procesem stochastycznym) o tej własności, że dla każdego ![]() ,
zmienna
,
zmienna ![]() jest mierzalna względem
jest mierzalna względem ![]() (mówimy, że proces
stochastyczny
(mówimy, że proces
stochastyczny ![]() jest adaptowany do filtracji
jest adaptowany do filtracji ![]() ). Dalej,
niech
). Dalej,
niech ![]() oraz
oraz
przy czym przyjmijmy konwencję ![]() . Funkcja
. Funkcja
![]() to moment pierwszego dojścia procesu
to moment pierwszego dojścia procesu ![]() do zbioru
do zbioru
![]() . Wówczas
. Wówczas ![]() jest momentem zatrzymania: dla każdego
jest momentem zatrzymania: dla każdego ![]() ,
,
Analogiczny fakt zachodzi, gdy zmienne ![]() przyjmują wartości w
przyjmują wartości w
![]() , albo ogólniej, w przestrzeni metrycznej
, albo ogólniej, w przestrzeni metrycznej ![]() .
.
Definicja 5.3
Załóżmy, że ![]() jest przestrzenią
probabilistyczną wyposażoną w filtrację
jest przestrzenią
probabilistyczną wyposażoną w filtrację ![]() i niech
i niech
![]() będzie momentem zatrzymania. Definiujemy
będzie momentem zatrzymania. Definiujemy
Intuicyjnie, ![]() opisuje wszystkie zdarzenia, które mogą
zajść do momentu
opisuje wszystkie zdarzenia, które mogą
zajść do momentu ![]() .
.
Uwagi:
1) ![]() jest
jest ![]() -ciałem,
-ciałem,
2) jeśli ![]() , to
, to ![]() .
.
Własności:
1) Jeśli ![]() ,
, ![]() są momentami zatrzymania, to
są momentami zatrzymania, to
![]() oraz
oraz ![]() też są momentami zatrzymania. Istotnie,
też są momentami zatrzymania. Istotnie,
2) Jeśli ![]() ,
, ![]() są takimi momentami zatrzymania, że
są takimi momentami zatrzymania, że
![]() , to
, to ![]() . Istotnie,
jeśli
. Istotnie,
jeśli ![]() , to dla każdego
, to dla każdego ![]() ,
,
i dwa ostatnie przecinane zbiory należą do ![]() .
.
3) Moment zatrzymania ![]() jest mierzalny względem
jest mierzalny względem ![]() .
Istotnie,
.
Istotnie,
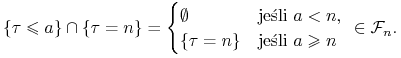 |
4) Załóżmy, że ![]() jest adaptowany do danej filtracji,
a
jest adaptowany do danej filtracji,
a ![]() jest momentem zatrzymania względem tej filtracji
spełniającym warunek
jest momentem zatrzymania względem tej filtracji
spełniającym warunek ![]() (jest to tzw. skończony
moment stopu. Wówczas zmienna
(jest to tzw. skończony
moment stopu. Wówczas zmienna ![]() jest mierzalna względem
jest mierzalna względem
![]() . Istotnie,
. Istotnie,
jako że oba przecinane zdarzenia należą do ![]() .
.
Przechodzimy do definicji głównych pojęć niniejszego rozdziału.
Definicja 5.4
Załóżmy, że ![]() jest przestrzenią
probabilistyczną wyposażoną w filtrację
jest przestrzenią
probabilistyczną wyposażoną w filtrację ![]() .
Załóżmy, że
.
Załóżmy, że ![]() jest adaptowanym ciągiem
całkowalnych zmiennych losowych. Mówimy, że
jest adaptowanym ciągiem
całkowalnych zmiennych losowych. Mówimy, że ![]() jest
jest
a) martyngałem, jeśli dla wszystkich ![]() ,
, ![]() zachodzi
zachodzi ![]() .
.
b) nadmartyngałem, jeśli dla wszystkich ![]() ,
, ![]() zachodzi
zachodzi ![]() .
.
c) podmartyngałem, jeśli dla wszystkich ![]() ,
, ![]() zachodzi
zachodzi ![]() .
.
Jeśli filtracja jest ustalona, to mówimy po prostu, że ![]() jest martyngałem (nad-, pod-), jeśli zachodzą powyższe warunki.
jest martyngałem (nad-, pod-), jeśli zachodzą powyższe warunki.
Uwagi:
a) ![]() jest martyngałem, wtedy i tylko
wtedy, gdy dla dowolnych
jest martyngałem, wtedy i tylko
wtedy, gdy dla dowolnych ![]() ,
, ![]() , oraz
, oraz ![]() zachodzi
zachodzi
Analogicznie dla nad- i podmartyngałów.
b) U nas ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
c) ![]() jest martyngałem wtedy i tylko wtedy, gdy jest nad- i
podmartyngałem.
jest martyngałem wtedy i tylko wtedy, gdy jest nad- i
podmartyngałem.
d) ![]() jest podmartyngałem wtedy i tylko wtedy, gdy
jest podmartyngałem wtedy i tylko wtedy, gdy ![]() jest
nadmartyngałem.
jest
nadmartyngałem.
e) Jeśli ![]() ,
, ![]() są martyngałami względem tej samej
filtracji i
są martyngałami względem tej samej
filtracji i ![]() , to
, to ![]() też jest martyngałem.
Analogiczny fakt zachodzi dla nad- i podmartyngałów, o ile
też jest martyngałem.
Analogiczny fakt zachodzi dla nad- i podmartyngałów, o ile ![]() .
.
f) Jeśli zbiór ![]() jest taki jak w b), to
jest taki jak w b), to ![]() jest
martyngałem wtedy i tylko wtedy, gdy dla wszystkich
jest
martyngałem wtedy i tylko wtedy, gdy dla wszystkich ![]() takich,
że
takich,
że ![]() , zachodzi
, zachodzi ![]() (analogiczny fakt
zachodzi dla nad- i podmartyngałów).
(analogiczny fakt
zachodzi dla nad- i podmartyngałów).
Dowód:
![]() oczywiste (szczególny przypadek).
oczywiste (szczególny przypadek).
![]() Załóżmy, że
Załóżmy, że ![]() ,
, ![]() . Wówczas
. Wówczas
![]() , a więc na mocy własności warunkowej wartości
oczekiwanej,
, a więc na mocy własności warunkowej wartości
oczekiwanej,
i dalej przez indukcję.
∎Przykłady:
1) Załóżmy, że ![]() są niezależnymi,
całkowalnymi zmiennymi losowymi o średniej
są niezależnymi,
całkowalnymi zmiennymi losowymi o średniej ![]() . Niech
. Niech
![]() i
i
![]() ,
, ![]() . Wówczas
. Wówczas
![]() jest martyngałem:
jest martyngałem:
2) Załóżmy, że ![]() jest całkowalną zmienną losową,
jest całkowalną zmienną losową, ![]() jest filtracją i niech
jest filtracją i niech ![]() dla
dla ![]() . Wówczas
. Wówczas
![]() jest martyngałem.
jest martyngałem.
Dowód:
Weźmy ![]() ,
, ![]() . Mamy, na mocy własności warunkowej
wartości oczekiwanej,
. Mamy, na mocy własności warunkowej
wartości oczekiwanej,
Martyngał taki jak w przykładzie 2) nazywamy prawostronnie
domkniętym. Czasami nazywa się tak martyngał wraz z domknięciem:
![]() , gdzie
, gdzie ![]() .
.
Stwierdzenie 5.1
Załóżmy, że ![]() jest martyngałem, a
jest martyngałem, a ![]() jest funkcją wypukłą taką, że
jest funkcją wypukłą taką, że ![]() jest zmienną całkowalną
dla każdego
jest zmienną całkowalną
dla każdego ![]() . Wówczas
. Wówczas ![]() jest
podmartyngałem.
jest
podmartyngałem.
Dowód:
Załóżmy, że ![]() ,
, ![]() . Wówczas, na mocy nierówności
Jensena,
. Wówczas, na mocy nierówności
Jensena,
Wniosek 5.1
Załóżmy, że ![]() jest martyngałem. Wówczas
jest martyngałem. Wówczas
a) Jeśli dla pewnego ![]() mamy, iż
mamy, iż ![]() dla wszystkich
dla wszystkich
![]() , to
, to ![]() jest podmartyngałem.
jest podmartyngałem.
b) Dla dowolnej liczby rzeczywistej ![]() , proces
, proces ![]() jest podmartyngałem. W szczególności,
jest podmartyngałem. W szczególności, ![]() ,
, ![]() są
podmartyngałami.
są
podmartyngałami.
Twierdzenie 5.1 (Dooba, ,,optional sampling”)
Załóżmy, że ![]() jest nadmartyngałem
(odp., martyngałem). Załóżmy, że
jest nadmartyngałem
(odp., martyngałem). Załóżmy, że ![]() są momentami
zatrzymania takimi, że
są momentami
zatrzymania takimi, że ![]() i
i ![]() jest ograniczony.
Wówczas mamy
jest ograniczony.
Wówczas mamy ![]() p.n. (odpowiednio,
p.n. (odpowiednio,
![]() p.n.).
p.n.).
Dowód:
Załóżmy, że ![]() . Zauważmy
najpierw, iż
. Zauważmy
najpierw, iż
![]() są całkowalne, gdyż
są całkowalne, gdyż
![]() . Zmienna
. Zmienna
![]() jest mierzalna względem
jest mierzalna względem ![]() , a zatem wystarczy
wykazać, że dla każdego
, a zatem wystarczy
wykazać, że dla każdego ![]() ,
,
(odpowiednio, z równością w miejscu nierówności w przypadku martyngałowym).
Załóżmy
najpierw, że ![]() . Mamy
. Mamy
(odpowiednio, ![]() ). Ostatnia nierówność bierze się stąd, iż
). Ostatnia nierówność bierze się stąd, iż
![]() .
.
Weźmy teraz dowolne ![]() . Definiujemy
. Definiujemy
![]() . Zmienne
. Zmienne ![]() są
momentami zatrzymania, a ponadto
są
momentami zatrzymania, a ponadto
oraz ![]() . Zatem dla każdego
. Zatem dla każdego
![]() ,
,
(z równościami w przypadku martyngałowym).
∎Twierdzenie 5.2 (Dooba o zbieżności p.n. nadmartyngałów)
Załóżmy, że proces ![]() jest nadmartyngałem
takim, że
jest nadmartyngałem
takim, że ![]() . Wówczas ciąg
. Wówczas ciąg ![]() jest
zbieżny p.n. do pewnej zmiennej losowej całkowalnej.
jest
zbieżny p.n. do pewnej zmiennej losowej całkowalnej.
Wniosek 5.2
a) Każdy nieujemny nadmartyngał ![]() (tzn. spełniający
(tzn. spełniający ![]() p.n. dla wszystkich
p.n. dla wszystkich ![]() ) jest zbieżny p.n.
) jest zbieżny p.n.
b) Jeśli ![]() jest podmartyngałem
spełniającym
jest podmartyngałem
spełniającym ![]() , to
, to ![]() jest zbieżny p.n.
jest zbieżny p.n.
c) Jeśli ![]() jest nadmartyngałem, to
warunek
jest nadmartyngałem, to
warunek ![]() jest równoważny warunkowi
jest równoważny warunkowi ![]() (tzn. ograniczoności ciągu
(tzn. ograniczoności ciągu ![]() w
w ![]() ).
).
Dowód wniosku:
a) jest oczywiste, b) wynika wprost z
twierdzenia Dooba poprzez przejście do procesu ![]() , który
jest nadmartyngałem. Zajmijmy się dowodem c). Implikacja
, który
jest nadmartyngałem. Zajmijmy się dowodem c). Implikacja ![]() jest oczywista.
jest oczywista. ![]() Mamy
Mamy ![]() skąd
skąd
W dowodzie twierdzenia o zbieżności będziemy używać
następujących obiektów.
Załóżmy, że ![]() jest ciągiem liczbowym i niech
jest ciągiem liczbowym i niech
![]() to ustalone liczby rzeczywiste. Określmy
to ustalone liczby rzeczywiste. Określmy
Liczba ![]() to moment
to moment ![]() -tego
przejścia w górę ciągu
-tego
przejścia w górę ciągu ![]() przez przedział
przez przedział ![]() . Niech teraz
. Niech teraz
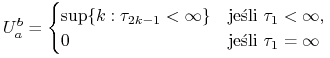 |
będzie liczbą przejść w górę ciągu ![]() przez przedział
przez przedział ![]() .
.
Lemat 5.1
Ciąg liczbowy ![]() jest zbieżny (być może do
jest zbieżny (być może do ![]() ) wtedy
i tylko wtedy, gdy dla wszystkich
) wtedy
i tylko wtedy, gdy dla wszystkich ![]() ,
, ![]() , mamy
, mamy
![]() .
.
Dowód:
![]() Przypuśćmy wbrew tezie, że
Przypuśćmy wbrew tezie, że ![]() jest zbieżny oraz
że istnieją
jest zbieżny oraz
że istnieją ![]() takie, że
takie, że ![]() oraz
oraz ![]() .
Wówczas znajdziemy nieskończony podciąg zawierający tylko wyrazy
mniejsze od
.
Wówczas znajdziemy nieskończony podciąg zawierający tylko wyrazy
mniejsze od ![]() oraz nieskończony podciąg zawierającego wyrazy tylko
większe od
oraz nieskończony podciąg zawierającego wyrazy tylko
większe od ![]() . Sprzeczność.
. Sprzeczność.
![]() Załóżmy, że
Załóżmy, że ![]() . Wówczas
istnieją
. Wówczas
istnieją ![]() takie, że
takie, że ![]() ; mamy wówczas
; mamy wówczas ![]() .
.
Lemat 5.2 (nierówność Dooba dla przejść w górę)
Załóżmy, że ![]() jest nadmartyngałem.
Wówczas dla dowolnych
jest nadmartyngałem.
Wówczas dla dowolnych ![]() ,
,
Dowód:
Załóżmy, że ![]() jest ciągiem momentów przejść ciągu
jest ciągiem momentów przejść ciągu
![]() przez
przedział
przez
przedział ![]() , i niech
, i niech ![]() będzie łączną liczbą
przejść. Widzimy, że
będzie łączną liczbą
przejść. Widzimy, że ![]() jest ciągiem momentów zatrzymania
(względem filtracji
jest ciągiem momentów zatrzymania
(względem filtracji ![]() ) oraz że
) oraz że ![]() jest zmienną losową.
Połóżmy
jest zmienną losową.
Połóżmy ![]() i wprowadźmy zmienne
i wprowadźmy zmienne
![]() ,
,
![]() . Z definicji widzimy, iż jeśli
. Z definicji widzimy, iż jeśli ![]() , to
, to ![]() . Ponadto, jeśli
. Ponadto, jeśli
![]() , to
, to
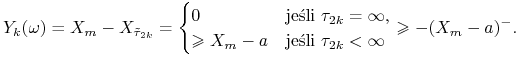 |
Wreszcie, jeśli ![]() , to
, to ![]() . Sumując
stronami powyższe związki dostajemy
. Sumując
stronami powyższe związki dostajemy
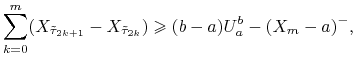 |
a zatem, biorąc wartość oczekiwaną,
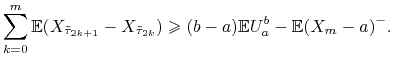 |
Lewa strona jest niedodatnia, na mocy twierdzenia Dooba (optional sampling); dostajemy zatem żądaną nierówność.
∎Dowód twierdzenia o zbieżności nadmartyngałów
Ustalmy ![]() ,
, ![]() .
Niech
.
Niech ![]() będzie łączną liczbą przejść nadmartyngału
będzie łączną liczbą przejść nadmartyngału
![]() w górę przez przedział
w górę przez przedział ![]() . Mamy
. Mamy
![]() . Na mocy drugiego z powyższych lematów,
. Na mocy drugiego z powyższych lematów,
Zatem, na mocy twierdzenia Lebesgue'a, ![]() , skąd
, skąd
![]() p.n. Zatem
p.n. Zatem
i na mocy pierwszego z powyższych lematów, ciąg ![]() jest
zbieżny p.n. Pozostaje tylko wykazać, że granica jest całkowalna;
wynika to natychmiast z lematu Fatou:
jest
zbieżny p.n. Pozostaje tylko wykazać, że granica jest całkowalna;
wynika to natychmiast z lematu Fatou:
Twierdzenie 5.3 (Nierówność maksymalna dla nadmartyngałów)
Załóżmy, że ![]() jest nadmartyngałem.
Wówczas dla każdego
jest nadmartyngałem.
Wówczas dla każdego ![]() ,
,
przy czym można wziąć ![]() , jeśli nadmartyngał jest nieujemny (tzn. zmienne
losowe
, jeśli nadmartyngał jest nieujemny (tzn. zmienne
losowe ![]() są nieujemne p.n.), niedodatni, bądź jest
martyngałem. W przypadku ogólnym nierówność zachodzi z
są nieujemne p.n.), niedodatni, bądź jest
martyngałem. W przypadku ogólnym nierówność zachodzi z ![]() .
.
Dowód:
Zauważmy, iż wystarczy szacować ![]() ,
przez proste przejście graniczne. Mamy
,
przez proste przejście graniczne. Mamy
Zajmiemy się oddzielnie prawdopodobieństwami występującymi po prawej stronie.
a) Niech ![]() . Na mocy twierdzenia Dooba
(optional sampling),
. Na mocy twierdzenia Dooba
(optional sampling),
Stąd
Stąd teza (gdy weźmiemy ![]() ) gdy
) gdy ![]() jest nieujemny.
jest nieujemny.
b) Rozważmy moment zatrzymania ![]() .
Z twierdzenia Dooba,
.
Z twierdzenia Dooba,
skąd
| (**) |
Stąd teza, gdy nadmartyngał jest niedodatni. Ponadto, jeśli ![]() jest martyngałem, to stosujemy powyższą nierówność do
niedodatniego nadmartyngału
jest martyngałem, to stosujemy powyższą nierówność do
niedodatniego nadmartyngału ![]() .
.
W ogólnym przypadku, wystarczy zsumować dwie końcowe nierówności
pochodzące z a) i b), dostać nierówność ze stałą ![]() .
.
Jeśli ![]() jest podmartyngałem, to stosując (**) dla
jest podmartyngałem, to stosując (**) dla ![]() dostajemy
dostajemy
Wniosek 5.3
Załóżmy, że ![]() jest podmartyngałem.
Wówczas dla
jest podmartyngałem.
Wówczas dla ![]() ,
,
Twierdzenie 5.4 (Nierówność maksymalna Dooba)
Załóżmy, że ![]() jest martyngałem
spełniającym warunek
jest martyngałem
spełniającym warunek ![]() ,
, ![]() dla pewnego
dla pewnego
![]() . Wówczas
. Wówczas
Dowód:
Niech ![]() ,
, ![]() . Mamy, stosując
poprzedni wniosek do podmartyngału
. Mamy, stosując
poprzedni wniosek do podmartyngału ![]() ,
dostajemy
,
dostajemy
Dzieląc obustronnie przez ![]() (jeśli ta liczba
jest zerem, to otrzymana poniżej nierówność także jest prawdziwa) dostajemy
(jeśli ta liczba
jest zerem, to otrzymana poniżej nierówność także jest prawdziwa) dostajemy
i wystarczy zbiec z ![]() .
.
Twierdzenie 5.5 (Zbieżność martyngałów w 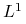 )
)
Załóżmy, że ![]() jest martyngałem.
następujące warunki
są równoważne.
jest martyngałem.
następujące warunki
są równoważne.
a) rodzina ![]() jest jednostajnie całkowalna.
jest jednostajnie całkowalna.
b) ![]() jest zbieżny w
jest zbieżny w ![]() .
.
c) Istnieje zmienna losowa ![]() taka, że
taka, że ![]() ,
,
![]() (czyli
martyngał jest prawostronnie domknięty).
(czyli
martyngał jest prawostronnie domknięty).
Co więcej, jeśli te warunki są spełnione, to ![]() jest zbieżny
p.n. do
jest zbieżny
p.n. do
| (*) |
i ![]() jest
jedyną zmienną losową mierzalną względem
jest
jedyną zmienną losową mierzalną względem ![]() -ciała
-ciała
![]() taką, że
taką, że ![]() ,
,
![]() .
.
Wniosek 5.4 (Twierdzenie Levy'ego)
Jeśli ![]() oraz
oraz ![]() jest filtracją, to
jest filtracją, to
![\mathbb{E}(X|\mathcal{F}_{n})\xrightarrow{\mbox{p.n. i w
}L^{1}}\mathbb{E}\left[X\Big|\sigma\left(\bigcup _{n}\mathcal{F}_{n}\right)\right].](wyklady/rp2/mi/mi842.png) |
Dowód twierdzenia o zbieżności
a)![]() b) Na mocy jednostajnej całkowalności dostajemy, iż
b) Na mocy jednostajnej całkowalności dostajemy, iż
![]() . Zatem na mocy twierdzenia Dooba martyngał
. Zatem na mocy twierdzenia Dooba martyngał ![]() jest zbieżny p.n., a zatem także według prawdopodobieństwa.
łącząc to z jednostajną całkowalnością dostajemy zbieżność w
jest zbieżny p.n., a zatem także według prawdopodobieństwa.
łącząc to z jednostajną całkowalnością dostajemy zbieżność w
![]() .
.
b)![]() c) Załóżmy, że
c) Załóżmy, że ![]() w
w ![]() . Dla
ustalonego
. Dla
ustalonego ![]() i
i ![]() mamy
mamy ![]() . Z drugiej strony,
. Z drugiej strony,
![]() w
w ![]() , gdyż operator warunkowej wartości
oczekiwanej jest kontrakcją w
, gdyż operator warunkowej wartości
oczekiwanej jest kontrakcją w ![]() : istotnie,
: istotnie,
Stąd ![]() .
.
c)![]() a) Pozostawiamy jako ćwiczenie.
a) Pozostawiamy jako ćwiczenie.
Pozostaje wykazać drugą część twierdzenia. Wiemy już, że warunki
a), b), c) pociągają za sobą, iż ![]() ,
,
![]() (gdzie
(gdzie ![]() jest granicą, w sensie zbieżności w
jest granicą, w sensie zbieżności w ![]() i p.n., martyngału
i p.n., martyngału ![]() ).
Oczywiście
).
Oczywiście ![]() jest mierzalna względem
jest mierzalna względem
![]() . Przypuśćmy teraz, że
. Przypuśćmy teraz, że ![]() jest całkowalną
zmienną losową, mierzalną względem tego
jest całkowalną
zmienną losową, mierzalną względem tego ![]() -ciała, dla
której
-ciała, dla
której ![]() ,
, ![]() . Zatem
. Zatem
![]() , skąd dla dowolnego
, skąd dla dowolnego ![]() i
dowolnego
i
dowolnego ![]() ,
,
Klasa ![]() jest
jest ![]() -układem. Klasa tych zbiorów
-układem. Klasa tych zbiorów ![]() , dla
których zachodzi powyższa równość, jest
, dla
których zachodzi powyższa równość, jest ![]() -układem. Z
lematu o
-układem. Z
lematu o ![]() -
-![]() układach mamy, iż powy'rsza równo'sć
całek zachodzi dla dowolnego
układach mamy, iż powy'rsza równo'sć
całek zachodzi dla dowolnego ![]() . Na mocy
mierzalności
. Na mocy
mierzalności ![]() oraz
oraz ![]() względem tego
względem tego ![]() -ciała, mamy,
iż
-ciała, mamy,
iż ![]() p.n.
p.n.
Wreszcie, pozostaje udowodnić równość (*). Jeśli ![]() ,
to
,
to
Na mocy powyższych rozważań o jednoznaczności, dostajemy (*). Dowód jest zakończony.
∎Wniosek 5.5 (Prawo 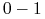 Kołmogorowa)
Kołmogorowa)
Załóżmy, że ![]() ,
, ![]() ,
, ![]() są niezależnymi zmiennymi
losowymi i
są niezależnymi zmiennymi
losowymi i ![]() dla
dla ![]() . Wówczas
jeśli
. Wówczas
jeśli ![]() , to
, to
![]() .
.
Dowód
Oczywiście ![]() jest mierzalne względem
jest mierzalne względem
![]() -ciała
-ciała ![]() . Zatem na
mocy twierdzenia Levy'ego,
. Zatem na
mocy twierdzenia Levy'ego,
![\mathbb{E}(1_{A}|\mathcal{F}_{n})\xrightarrow{\mbox{p.n. i w }L^{1}}\mathbb{E}\left[1_{A}\Big|\sigma\left(\bigcup _{{n=1}}^{\infty}\mathcal{F}_{n}\right)\right]=1_{A}.](wyklady/rp2/mi/mi1021.png) |
Ale z drugiej strony ![]() jest niezależne od
jest niezależne od ![]() , bo
, bo ![]() , a to
, a to ![]() -ciało jest niezależne
od
-ciało jest niezależne
od ![]() . Stąd
. Stąd
a zatem ![]() lub
lub ![]() .
.
Zajmiemy się teraz zbieżnością w ![]() dla
dla ![]() .
.
Twierdzenie 5.6
Załóżmy, że ![]() jest martyngałem i
jest martyngałem i
![]() . Następujące warunki są równoważne.
. Następujące warunki są równoważne.
a) ![]() .
.
b) Rodzina ![]() jest jednostajnie całkowalna.
jest jednostajnie całkowalna.
c) Martyngał ![]() jest zbieżny w
jest zbieżny w ![]() .
.
d) Istnieje ![]() taka, że
taka, że ![]() .
.
Jeśli te warunki są spełnione, to ![]() jest zbieżny p.n. do zmiennej losowej
jest zbieżny p.n. do zmiennej losowej
![]() .
.
a)![]() b) Wiemy, że
b) Wiemy, że ![]() , czyli
, czyli
![]() , skąd dostajemy b) (istnienie majoranty
całkowalnej).
, skąd dostajemy b) (istnienie majoranty
całkowalnej).
b)![]() c) Mamy, iż
c) Mamy, iż
a zatem na mocy twierdzenia Dooba o zbieżności nadmartyngałów,
![]() jest zbieżny p.n.. Dokładając jednostajną całkowalność
dostajemy c).
jest zbieżny p.n.. Dokładając jednostajną całkowalność
dostajemy c).
c)![]() d) Mamy
d) Mamy ![]() w
w ![]() . Przy ustalonym
. Przy ustalonym
![]() oraz
oraz ![]() ,
, ![]() . Ponieważ
. Ponieważ ![]() jest
kontrakcją w
jest
kontrakcją w ![]() , więc
, więc ![]() .
.
d)![]() a) Mamy
a) Mamy
5.1. Zadania
1. Załóżmy, że ![]() jest filtracją, a
jest filtracją, a ![]() jest
ciągiem zmiennych losowych adaptowanych do tej filtracji. Niech
jest
ciągiem zmiennych losowych adaptowanych do tej filtracji. Niech ![]() będzie podzbiorem borelowskim
będzie podzbiorem borelowskim ![]() .
.
a) Udowodnić, że ![]() jest momentem
zatrzymania.
jest momentem
zatrzymania.
b) Udowodnić, że dla dowolnego momentu zatrzymania ![]() , zmienna
, zmienna
![]() też jest momentem zatrzymania.
też jest momentem zatrzymania.
2. Dany jest ciąg ![]() niezależnych zmiennych losowych
o rozkładzie
niezależnych zmiennych losowych
o rozkładzie ![]() . Niech
. Niech
(przyjmujemy ![]() ).
Czy
).
Czy ![]() ,
, ![]() są momentami zatrzymania?
są momentami zatrzymania?
3. Zmienne ![]() ,
, ![]() są momentami zatrzymania
względem filtracji
są momentami zatrzymania
względem filtracji ![]() . Czy
zmienne
. Czy
zmienne ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() są momentami zatrzymania?
są momentami zatrzymania?
4. Dany jest ciąg ![]() niezależnych zmiennych losowych
o tym samym rozkładzie
niezależnych zmiennych losowych
o tym samym rozkładzie ![]() .
Niech
.
Niech ![]() i
i ![]() dla
dla ![]() . Niech
. Niech
![]() będzie naturalną filtracją generowaną przez ciąg
będzie naturalną filtracją generowaną przez ciąg ![]() .
.
a) Udowodnić,że ![]() oraz
oraz ![]() są martyngałami.
są martyngałami.
b) Wyznaczyć taką wartość parametru ![]() , by ciąg
, by ciąg ![]() był martyngałem.
był martyngałem.
c) Udowodnić, że dla ![]() , ciąg
, ciąg ![]() jest nadmartyngałem.
jest nadmartyngałem.
5. Załóżmy, że ![]() jest ciągiem niezależnych
zmiennych loswych o tym samym rozkładzie o średniej
jest ciągiem niezależnych
zmiennych loswych o tym samym rozkładzie o średniej ![]() . Niech
. Niech
![]() ,
, ![]() dla
dla ![]() .
Udowodnić, że ciąg
.
Udowodnić, że ciąg ![]() jest martyngałem.
jest martyngałem.
6. Dany jest ciąg ![]() adaptowany do filtracji
adaptowany do filtracji ![]() .
Udowodnić, że ciąg
.
Udowodnić, że ciąg ![]() jest martyngałem wtedy i tylko wtedy gdy
dla każdego ograniczonego momentu zatrzymania
jest martyngałem wtedy i tylko wtedy gdy
dla każdego ograniczonego momentu zatrzymania ![]() zachodzi
równość
zachodzi
równość ![]() .
.
7. Dany jest martyngał ![]() oraz
moment zatrzymania
oraz
moment zatrzymania ![]() . Udowodnić, że
. Udowodnić, że ![]() też jest martyngałem.
też jest martyngałem.
8. Egzaminator przygotował ![]() zestawów pytań. Studenci
kolejno losują kartki z pytaniami, przy czym zestaw raz wyciągnięty
nie wraca do ponownego losowania. tudent nauczył się odpowiedzi na
zestawów pytań. Studenci
kolejno losują kartki z pytaniami, przy czym zestaw raz wyciągnięty
nie wraca do ponownego losowania. tudent nauczył się odpowiedzi na
![]() zestawów
zestawów ![]() . Obserwując przebieg egzaminu chce
przystąpić do niego w takim momencie, żeby zmaksymalizować szanse
zdania. Czy istnieje strategia optymalna?
. Obserwując przebieg egzaminu chce
przystąpić do niego w takim momencie, żeby zmaksymalizować szanse
zdania. Czy istnieje strategia optymalna?
9. Gramy w orła i reszkę symetryczną monetą. Przed ![]() -tą
grą, opierając się ewentualnie na wynikach poprzednich gier, sami
ustalamy stawkę w
-tą
grą, opierając się ewentualnie na wynikach poprzednich gier, sami
ustalamy stawkę w ![]() -tej grze: wybieramy
-tej grze: wybieramy ![]() ,
, ![]() , i
jeśli wypadnie orzeł dostajemy
, i
jeśli wypadnie orzeł dostajemy ![]() zł, jeśli reszka - płacimy
zł, jeśli reszka - płacimy
![]() zł. Niech
zł. Niech ![]() oznacza łączną wygraną po
oznacza łączną wygraną po ![]() grach.
Udowodnić, że
grach.
Udowodnić, że ![]() jest martyngałem (względem naturalnej
filtracji).
jest martyngałem (względem naturalnej
filtracji).
10. Mamy ![]() zł w monetach
zł w monetach ![]() zł, a potrzebujemy pilnie
zł, a potrzebujemy pilnie
![]() zł. Jedynym sposobem zdobycia tych pieniędzy jest gra w
zł. Jedynym sposobem zdobycia tych pieniędzy jest gra w ![]() karty z szulerem (który wygrywa z prawdopodobieństwem
karty z szulerem (który wygrywa z prawdopodobieństwem ![]() ). Szuler
gotów jest grać z nami wiele razy o dowolne stawki, jakie jesteśmy w
stanie założyć (przyjmijmy dla uproszczenia, że stawka nie
przekracza
). Szuler
gotów jest grać z nami wiele razy o dowolne stawki, jakie jesteśmy w
stanie założyć (przyjmijmy dla uproszczenia, że stawka nie
przekracza ![]() zł). Udowodnić, że niezależnie od wyboru strategii
nasze szanse na uzyskanie brakujących
zł). Udowodnić, że niezależnie od wyboru strategii
nasze szanse na uzyskanie brakujących ![]() zł nie przekraczają
zł nie przekraczają
![]() .
.
11. (Tożsamość Walda). Dany jest ciąg ![]() całkowalnych zmiennych losowych o tym samym
rozkładzie, adaptowany do filtracji
całkowalnych zmiennych losowych o tym samym
rozkładzie, adaptowany do filtracji ![]() , taki,
że zmienna
, taki,
że zmienna ![]() jest niezależna od
jest niezależna od ![]() . Udowodnić, że dla
dowolnego momentu zatrzymania
. Udowodnić, że dla
dowolnego momentu zatrzymania ![]() takiego, że
takiego, że ![]() ,
zachodzi wzór
,
zachodzi wzór
12. Załóżmy, że ![]() są niezależnymi
zmiennymi losowymi o średniej
są niezależnymi
zmiennymi losowymi o średniej ![]() , spełniającymi warunek
, spełniającymi warunek
![]() . Udowodnić, że szereg
. Udowodnić, że szereg
![]() jest zbieżny p.n.
jest zbieżny p.n.
W zadaniach 13 - 17 poniżej rozpatrujemy ciąg ![]() ,
, ![]() ,
,
![]() niezależnych zmiennych losowych o rozkładzie
niezależnych zmiennych losowych o rozkładzie
![]() , i oznaczamy
, i oznaczamy ![]() ,
,
![]() dla
dla ![]() . Dla
. Dla ![]() ,
,
![]() , niech
, niech ![]() oraz
oraz
![]() .
.
13. Załóżmy, że ![]() i niech
i niech ![]() . Korzystając z teorii
martyngałów obliczyć
. Korzystając z teorii
martyngałów obliczyć ![]() ,
, ![]() oraz
oraz ![]() .
.
14. Rozwiązać zadanie 13 przy założeniu ![]() .
.
15. Udowodnić, że ![]() .
.
16. Załóżmy, że ![]() oraz
oraz ![]() jest całkowalnym momentem
zatrzymania. Udowodnić, że
jest całkowalnym momentem
zatrzymania. Udowodnić, że ![]() oraz
oraz ![]() .
.
17. Zbadać zbieżność p.n. oraz w ![]() nadmartyngału
nadmartyngału
![]() (por. zadanie 4 c)).
(por. zadanie 4 c)).
18. Zmienne ![]() ,
, ![]() ,
, ![]() , są niezależne i mają
ten sam rozkład skoncentrowany na liczbach nieujemnych, różny od
, są niezależne i mają
ten sam rozkład skoncentrowany na liczbach nieujemnych, różny od
![]() , o średniej
, o średniej ![]() .
Udowodnić, że ciąg
.
Udowodnić, że ciąg ![]() jest
zbieżny p.n., ale nie jest zbieżny w
jest
zbieżny p.n., ale nie jest zbieżny w ![]() .
.
19. W pojemniku znajduje się pewna liczba cząstek, z
których każda w chwili ![]() z równym prawdopodobieństwem albo
dzieli się na dwie, albo ginie. W chwili
z równym prawdopodobieństwem albo
dzieli się na dwie, albo ginie. W chwili ![]() liczba cząstek wynosi
liczba cząstek wynosi
![]() . Udowodnić, że z prawdopodobieństwem
. Udowodnić, że z prawdopodobieństwem ![]() po pewnym czasie
wszystkie cząstki zginą, tzn. w pojemniku nie będzie ani jednej
cząstki.
po pewnym czasie
wszystkie cząstki zginą, tzn. w pojemniku nie będzie ani jednej
cząstki.




