Zagadnienia
6. Łańcuchy Markowa
6.1. Podstawowe definicje
Zajmiemy się teraz kolejną ważną klasą procesów stochastycznych: łańcuchami Markowa.
Niech ![]() będzie ,,przestrzenią stanów”: skończonym lub
przeliczalnym zbiorem. Jego elementy będziemy oznaczać literami
będzie ,,przestrzenią stanów”: skończonym lub
przeliczalnym zbiorem. Jego elementy będziemy oznaczać literami ![]() ,
,
![]() ,
, ![]() bądź
bądź ![]() ,
, ![]() ,
, ![]() .
.
Definicja 6.1
Macierz ![]() nazywamy macierzą
stochastyczną, jeśli
nazywamy macierzą
stochastyczną, jeśli ![]() dla wszystkich
dla wszystkich ![]() ,
, ![]() oraz
oraz ![]() dla każdego
dla każdego ![]() .
.
Definicja 6.2
Załóżmy, że ![]() jest przestrzenią
probabilistyczną,
jest przestrzenią
probabilistyczną, ![]() ,
, ![]() są j.w., ustalone. Jednorodnym łańcuchem
Markowa o wartościach w
są j.w., ustalone. Jednorodnym łańcuchem
Markowa o wartościach w ![]() i macierzy przejścia
i macierzy przejścia ![]() nazywamy ciąg
nazywamy ciąg
![]() zmiennych losowych takich, że
zmiennych losowych takich, że
dla wszystkich ![]() ,
, ![]() ,
, ![]() ,
, ![]() takich, że zdarzenie
warunkujące ma dodatnie prawdopodobieństwo. Równoważnie,
takich, że zdarzenie
warunkujące ma dodatnie prawdopodobieństwo. Równoważnie,
Liczba ![]() jest
prawdopodobieństwem przejścia ze stanu
jest
prawdopodobieństwem przejścia ze stanu ![]() do stanu
do stanu ![]() w jednym
kroku.
w jednym
kroku.
Przykłady:
1) Załóżmy, że ![]() ,
, ![]() ,
, ![]() ,
, ![]() są niezależnymi
zmiennymi losowymi o tym samym rozkładzie, przyjmującymi wartości w
zbiorze
są niezależnymi
zmiennymi losowymi o tym samym rozkładzie, przyjmującymi wartości w
zbiorze ![]() , przy czym
, przy czym ![]() dla
dla ![]() . Wówczas
. Wówczas
a zatem ![]() jest łańcuchem Markowa; mamy
jest łańcuchem Markowa; mamy
![P=\left[\begin{array}[]{ccc}p_{1}&p_{2}&\ldots\\
p_{1}&p_{2}&\ldots\\
p_{1}&p_{2}&\ldots\\
\ldots\end{array}\right].](wyklady/rp2/mi/mi1068.png) |
2) (Błądzenie losowe) Załóżmy, że ![]() ,
, ![]() ,
, ![]() są niezależnymi zmiennymi
losowymi o rozkładzie
są niezależnymi zmiennymi
losowymi o rozkładzie ![]() ,
,
![]() . Niech
. Niech ![]() ,
,
![]() dla
dla ![]() . Mamy
. Mamy
3) (Błądzenie z pochłanianiem na brzegu). Załóżmy, że ![]() ,
, ![]() jak poprzednio, przy czym po dojściu do
jak poprzednio, przy czym po dojściu do ![]() bądź
bądź ![]() proces zatrzymuje się. Otrzymany ciąg zmiennych losowych
także jest łańcuchem Markowa. Mamy
proces zatrzymuje się. Otrzymany ciąg zmiennych losowych
także jest łańcuchem Markowa. Mamy ![]() i
i
![P=\left[\begin{array}[]{ccccccc}1&0&0&0&\ldots&0&0\\
q&0&p&0&\ldots&0&0\\
0&q&0&p&\ldots&0&0\\
0&0&q&0&\ldots&0&0\\
\ldots\\
0&0&0&0&\ldots&0&p\\
0&0&0&0&\ldots&0&1\end{array}\right]](wyklady/rp2/mi/mi1274.png) |
4) (Błądzenie z odbiciem od brzegu). Niech ![]() ,
, ![]() jak poprzednio, przy czym po dojściu do
jak poprzednio, przy czym po dojściu do ![]() przechodzimy do
przechodzimy do ![]() ,
po dojściu do
,
po dojściu do ![]() przechodzimy do
przechodzimy do ![]() . Wówczas otrzymany proces
jest łańcuchem Markowa o macierzy przejścia jak poprzednio, tyle
że pierwszy wiersz to
. Wówczas otrzymany proces
jest łańcuchem Markowa o macierzy przejścia jak poprzednio, tyle
że pierwszy wiersz to ![]() , a ostatni -
, a ostatni -
![]() .
.
5) (Model dyfuzji cząstek).
Danych jest ![]() cząstek w dwóch pojemnikach: I i II. Co
jednostkę czasu losowo wybrana cząstka przemieszcza się z jednego
pojemnika do drugiego.
cząstek w dwóch pojemnikach: I i II. Co
jednostkę czasu losowo wybrana cząstka przemieszcza się z jednego
pojemnika do drugiego.
Niech ![]() oznacza liczbę cząstek w pojemniku
oznacza liczbę cząstek w pojemniku ![]() w chwili
w chwili ![]() .
Przestrzeń stanów to
.
Przestrzeń stanów to ![]() oraz
oraz
Pozostałe ![]() są równe
są równe ![]() :
:
![P=\left[\begin{array}[]{cccccc}0&1&0&\ldots&0&0\\
1/n&0&1-1/n&\ldots&0&0\\
0&2/n&0&\ldots&0&0\\
0&0&3/n&\ldots&0&0\\
\ldots 0&0&0&\ldots&0&1/n\\
0&0&0&\ldots&1&0\end{array}\right].](wyklady/rp2/mi/mi1242.png) |
Stwierdzenie 6.1
Załóżmy, że ![]() jest łańcuchem Markowa z macierzą przejścia
jest łańcuchem Markowa z macierzą przejścia
![]() . Wówczas dla każdej ograniczonej funkcji
. Wówczas dla każdej ograniczonej funkcji ![]() i
dowolnego
i
dowolnego ![]() ,
,
| (*) |
Dowód:
Mamy
Stąd równość skrajnych stron w (*). Aby otrzymać prawą
równość, wystarczy powtórzyć powyższe rozumowanie z warunkowaniem
tylko po zmiennej ![]() .
.
Twierdzenie 6.1
Załóżmy, że ![]() ,
, ![]() ,
, ![]() - jak wyżej. Wówczas dla wszystkich
- jak wyżej. Wówczas dla wszystkich
![]() ,
, ![]() ,
, ![]() ,
,
gdzie ![]() . Macierz tę możemy
interpretować jako macierz przejścia w
. Macierz tę możemy
interpretować jako macierz przejścia w ![]() krokach.
krokach.
Dowód:
Stosujemy indukcję ze względu na ![]() . Dla
. Dla ![]() dostajemy definicję
łańcucha Markowa. Przypuśćmy, że teza zachodzi dla pewnego
dostajemy definicję
łańcucha Markowa. Przypuśćmy, że teza zachodzi dla pewnego ![]() . Mamy
. Mamy
Wniosek 6.1 (Równanie Chapmana-Kołmogorowa)
Dla wszystkich ![]() oraz
oraz ![]() ,
,
Dowód:
Wynika to natychmiast z równości
![]() .
.
Stwierdzenie 6.2
Przy założeniach jak wyżej, dla dowolnego ![]() oraz
oraz
![]() ,
,
Dowód:
Mamy
itd.
∎Definicja 6.3
Rozkład zmiennej ![]() nazywamy rozkładem początkowym. Jest on
jednoznacznie wyznaczony przez ciąg
nazywamy rozkładem początkowym. Jest on
jednoznacznie wyznaczony przez ciąg ![]() liczb
nieujemnych o sumie
liczb
nieujemnych o sumie ![]() .
.
Podane niżej twierdzenie mówi, iż każda macierz stochastyczna i rozkład początkowy prowadzą do pewnego łańcucha Markowa. Twierdzenie to pozostawimy bez dowodu.
Twierdzenie 6.2
Niech ![]() będzie zbiorem co najwyżej przeliczalnym. Wówczas dla
każdej macierzy stochatycznej
będzie zbiorem co najwyżej przeliczalnym. Wówczas dla
każdej macierzy stochatycznej ![]() oraz miary probabilistycznej
oraz miary probabilistycznej ![]() na
na ![]() istnieje przestrzeń probabilistyczna i określony na niej
łańcuch Markowa o macierzy przejścia
istnieje przestrzeń probabilistyczna i określony na niej
łańcuch Markowa o macierzy przejścia ![]() i rozkładzie początkowym
i rozkładzie początkowym
![]() .
.
6.2. Klasyfikacja stanów
Mówimy, że stan ![]() jest osiągalny ze stanu
jest osiągalny ze stanu ![]() , jeśli
, jeśli
![]() dla pewnego
dla pewnego ![]() . Mówimy, że stany
. Mówimy, że stany ![]() oraz
oraz ![]() się komunikują, jeśli
się komunikują, jeśli ![]() jest osiągalny z
jest osiągalny z ![]() oraz
oraz ![]() jest
osiągalny z
jest
osiągalny z ![]() . Stan
. Stan ![]() jest nieistotny, jeśli istnieje taki stan
jest nieistotny, jeśli istnieje taki stan
![]() , że
, że ![]() jest osiągalny z
jest osiągalny z ![]() oraz
oraz ![]() nie jest osiągalny z
nie jest osiągalny z ![]() .
Jak łatwo sprawdzić, korzystając z równania Chapmana-Kołmogorowa,
relacja ,,osiągalności” jest przechodnia: istotnie, jeśli
.
Jak łatwo sprawdzić, korzystając z równania Chapmana-Kołmogorowa,
relacja ,,osiągalności” jest przechodnia: istotnie, jeśli ![]() jest
osiągalny z
jest
osiągalny z ![]() oraz
oraz ![]() jest osiągalny z
jest osiągalny z ![]() , to dla pewnych
, to dla pewnych
![]() ,
, ![]() ,
, ![]() i
i ![]() , a zatem
, a zatem
Aby zilustrować powyższe definicje, odnotujmy, iż dla błądzenia
losowego po liczbach całkowitych (przykład 2 powyżej), wszystkie
stany wzajemnie się komunikują. Natomiast w przypadku pochłaniania
na brzegu (przykład 3), stany ![]() są nieistotne.
są nieistotne.
Zbiór stanów ![]() nazywamy zamkniętym, jeśli dla dowolnego
nazywamy zamkniętym, jeśli dla dowolnego ![]() oraz
oraz ![]() , stan
, stan ![]() nie jest osiągalny ze stanu
nie jest osiągalny ze stanu ![]() (innymi
słowy, startując ze stanu wewnątrz
(innymi
słowy, startując ze stanu wewnątrz ![]() , z prawdopodobieństwem
, z prawdopodobieństwem ![]() nie wychodzimy nigdy z tego zbioru). Jeśli stan
nie wychodzimy nigdy z tego zbioru). Jeśli stan ![]() ma tę
własność, że zbiór
ma tę
własność, że zbiór ![]() jest zamknięty (tzn. mamy
jest zamknięty (tzn. mamy
![]() dla wszystkich
dla wszystkich ![]() ), to stan ten nazywamy
pochłaniającym. łańcuch Markowa nazywamy nieprzywiedlnym, jeśli
wszystkie stany komunikują się ze sobą. Przykładowo, łańcuch
Markowa pojawiający się w modelu dyfuzji cząstek (przykład 5) jest
nieprzywiedlny.
), to stan ten nazywamy
pochłaniającym. łańcuch Markowa nazywamy nieprzywiedlnym, jeśli
wszystkie stany komunikują się ze sobą. Przykładowo, łańcuch
Markowa pojawiający się w modelu dyfuzji cząstek (przykład 5) jest
nieprzywiedlny.
Uwaga: Załóżmy, że ![]() jest zamkniętym zbiorem stanów
łańcucha Markowa o macierzy przejścia
jest zamkniętym zbiorem stanów
łańcucha Markowa o macierzy przejścia ![]() .
Wówczas możemy rozpatrzyć łańcuch Markowa ,,zawężony” do
.
Wówczas możemy rozpatrzyć łańcuch Markowa ,,zawężony” do ![]() :
jako nową przestrzeń stanów bierzemy zbiór
:
jako nową przestrzeń stanów bierzemy zbiór ![]() , a macierz
przejścia zadana jest przez
, a macierz
przejścia zadana jest przez ![]() (wykreślamy z macierzy
(wykreślamy z macierzy ![]() wiersze i kolumny odpowieadające stanom
nienależącym do
wiersze i kolumny odpowieadające stanom
nienależącym do ![]() ). Przykładowo, załóżmy, że macierz przejścia
łańcucha na
). Przykładowo, załóżmy, że macierz przejścia
łańcucha na ![]() wynosi
wynosi
![\left[\begin{array}[]{cccc}1/2&1/2&0&0\\
1/4&3/4&0&0\\
0&1/3&1/2&1/6\\
1/5&1/5&2/5&1/5\end{array}\right].](wyklady/rp2/mi/mi1121.png) |
Jak łatwo zauważyć, zbiór ![]() jest zamknięty i indukuje
łańcuch Markowa o wartościach w tym zbiorze i macierzy przejścia
jest zamknięty i indukuje
łańcuch Markowa o wartościach w tym zbiorze i macierzy przejścia
![]() .
.
Niech
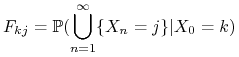 |
będzie prawdopodobieństwem tego, że startując z ![]() łańcuch
dojdzie kiedyś do stanu
łańcuch
dojdzie kiedyś do stanu ![]() . Mamy
. Mamy
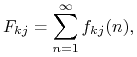 |
gdzie
jest prawdopodobieństwem że startując z ![]() łańcuch dochodzi do
łańcuch dochodzi do ![]() po raz pierwszy w chwili
po raz pierwszy w chwili ![]() .
.
Definicja 6.4
Stan ![]() nazywamy powracającym, jeśli
nazywamy powracającym, jeśli ![]() . Stan
. Stan ![]() nazywamy
chwilowym (tranzytywnym), jeśli
nazywamy
chwilowym (tranzytywnym), jeśli ![]() .
.
Niech ![]() będzie zmienną losową
zliczającą ile razy proces
będzie zmienną losową
zliczającą ile razy proces ![]() był w stanie
był w stanie ![]() (nie biorąc pod
uwagę zmiennej
(nie biorąc pod
uwagę zmiennej ![]() ). Mamy
następujący fakt.
). Mamy
następujący fakt.
Stwierdzenie 6.3
(i) Stan ![]() jest powracający wtedy i tylko wtedy, gdy
jest powracający wtedy i tylko wtedy, gdy
![]() .
.
(ii) Stan ![]() jest chwilowy wtedy i tylko wtedy, gdy
jest chwilowy wtedy i tylko wtedy, gdy
![]() .
.
Dowód:
Niech ![]() proces
proces ![]() był w stanie
był w stanie ![]() co najmniej
co najmniej ![]() razy
razy![]() . Oczywiście
. Oczywiście ![]() , a zatem z twierdzenia o
ciagłości
, a zatem z twierdzenia o
ciagłości
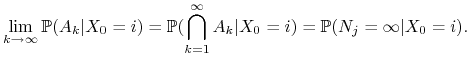 |
Wykażemy, że
| (*) |
Wówczas dostaniemy (stosując tę równość dla ![]() ), iż
), iż
![]() wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy ![]() (to teza (i)) oraz
(to teza (i)) oraz ![]() wtedy i tylko
wtedy, gdy
wtedy i tylko
wtedy, gdy ![]() (co jest równoważne tezie (ii)).
(co jest równoważne tezie (ii)).
Pozostaje więc udowodnić (*). Intuicyjnie ten wynik jest jasny: jeśli mamy ![]() razy odwiedzić stan
razy odwiedzić stan ![]() (przy
założeniu, że startujemy z
(przy
założeniu, że startujemy z ![]() ), to musimy dojść z
), to musimy dojść z ![]() do
do
![]() , a potem
, a potem ![]() razy powrócić do
razy powrócić do ![]() po pewnych liczbach kroków.
Formalnie, ustalmy
po pewnych liczbach kroków.
Formalnie, ustalmy ![]() . Mamy
. Mamy
Podstawmy ![]() ,
, ![]() . Mamy, dla
. Mamy, dla ![]() ,
,
Uwaga: W szczególności, ![]() jeśli
jeśli ![]() jest stanem chwilowym. Zatem w przypadku stanu chwilowego,
proces odwiedza go skończenie wiele razy niezależnie od punktu
startowego.
jest stanem chwilowym. Zatem w przypadku stanu chwilowego,
proces odwiedza go skończenie wiele razy niezależnie od punktu
startowego.
Podane niżej twierdzenie charakteryzuje stany chwilowe i powracające w
terminach macierzy przejścia. Wprowadźmy, dla każdego ![]() ,
liczbę
,
liczbę ![]() . Na mocy twierdzenia
Fubiniego (dla funkcji nieujemnych),
. Na mocy twierdzenia
Fubiniego (dla funkcji nieujemnych),
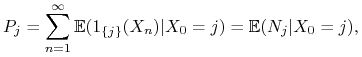 |
czyli ![]() jest średnim czasem przebywania łańcucha w stanie
jest średnim czasem przebywania łańcucha w stanie ![]() (przy założeniu startowania z tego stanu), nie licząc zmiennej
(przy założeniu startowania z tego stanu), nie licząc zmiennej
![]() .
.
Twierdzenie 6.3
(i) Stan ![]() jest chwilowy wtedy i tylko wtedy, gdy
jest chwilowy wtedy i tylko wtedy, gdy ![]() .
.
(ii) Stan ![]() jest powracający wtedy i tylko wtedy, gdy
jest powracający wtedy i tylko wtedy, gdy ![]() .
.
Dowód:
Zauważmy, iż na mocy wzoru na prawdopodobieństwo całkowite,
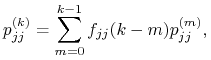 |
gdzie przyjmujemy ![]() .
Zatem, na mocy twierdzenia Fubiniego (dla funkcji nieujemnych),
.
Zatem, na mocy twierdzenia Fubiniego (dla funkcji nieujemnych),
czyli, równoważnie,
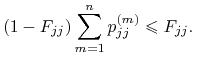 |
(\Delta) |
Jeśli stan ![]() jest chwilowy, to (
jest chwilowy, to (![]() ) daje, iż
) daje, iż
I w drugą stronę: jeśli ![]() , czyli
, czyli ![]() ,
to
,
to ![]() i na mocy poprzedniego twierdzenia
i na mocy poprzedniego twierdzenia
![]() jest stanem chwilowym. To dowodzi (i). Część (ii) jest
konsekwencją tego, że każdy stan jest albo chwilowy, albo
powracający oraz tego, że
jest stanem chwilowym. To dowodzi (i). Część (ii) jest
konsekwencją tego, że każdy stan jest albo chwilowy, albo
powracający oraz tego, że ![]() jest albo skończone, albo nie.
jest albo skończone, albo nie.
Przykład: Zbadamy błądzenie losowe po liczbach całkowitych. Mamy
na mocy wzoru Stirlinga. Ponadto, ![]() . Stąd
. Stąd
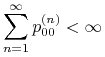 |
wtedy i tylko wtedy,gdy ![]() . Zatem
. Zatem ![]() jest stanem powracającym
wtedy i tylko wtedy, gdy
jest stanem powracającym
wtedy i tylko wtedy, gdy ![]() .
.
W przypadku gdy wszystkie stany komunikują się wzajemnie, stany muszą być tego samego typu.
Twierdzenie 6.4
Załóżmy, że łańcuch Markowa jest nieprzywiedlny. Wówczas jeśli jeden stan jest chwilowy, to wszystkie są chwilowe; jeśli jeden stan jest powracający, to wszystkie są powracające.
Możemy więc mówić o łańcuchach określonego typu: chwilowych i powracających.
Weźmy dwa stany ![]() ,
, ![]() . Istnieją liczby całowite dodatnie
. Istnieją liczby całowite dodatnie ![]() ,
, ![]() takie, że
takie, że ![]() ,
, ![]() . Dla
. Dla ![]() mamy
mamy
i podobnie ![]() . Zatem dla
. Zatem dla
![]() ,
,
czyli asymptotyczne zachowanie ciągów ![]() oraz
oraz
![]() jest takie samo; w szczególności,
jest takie samo; w szczególności, ![]() wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
![]() .
.
Na zakończenie - następujący fakt dotyczący struktury stanów łańcucha Markowa ze względu na stany chwilowe i powracające (bez dowodu).
Stwierdzenie 6.4
Przestrzeń stanów ![]() łańcucha Markowa możemy jednoznacznie
przedstawić w postaci
łańcucha Markowa możemy jednoznacznie
przedstawić w postaci
gdzie ![]() jest zbiorem stanów chwilowych, a
jest zbiorem stanów chwilowych, a ![]() ,
, ![]() są
nieprzywiedlnymi zamkniętymi zbiorami stanów powracających.
są
nieprzywiedlnymi zamkniętymi zbiorami stanów powracających.
Przy danym rozbiciu przestrzeni ![]() jak w powyższym stwierdzeniu, z
prawdopodobieństwem
jak w powyższym stwierdzeniu, z
prawdopodobieństwem ![]() łańcuch Markowa zachowuje się następująco. Jeśli startuje on w
zbiorze
łańcuch Markowa zachowuje się następująco. Jeśli startuje on w
zbiorze ![]() ,
, ![]() , to nigdy go nie opuszcza i odwiedza wszystkie
elementy tego zbioru; jeśli startuje on w zbiorze
, to nigdy go nie opuszcza i odwiedza wszystkie
elementy tego zbioru; jeśli startuje on w zbiorze ![]() , to albo
pozostaje tam na zawsze (co może mieć miejsce tylko wtedy, gdy
, to albo
pozostaje tam na zawsze (co może mieć miejsce tylko wtedy, gdy ![]() ma
nieskończenie wiele elementów), albo po
skończonej liczbie kroków trafia do jednego ze zbiorów
ma
nieskończenie wiele elementów), albo po
skończonej liczbie kroków trafia do jednego ze zbiorów ![]() , i
pozostaje tam na zawsze.
, i
pozostaje tam na zawsze.
6.3. Rozkłady stacjonarne i twierdzenie ergodyczne
Definicja 6.5
Załóżmy, że ![]() jest macierzą stochastyczną. Rozkład
jest macierzą stochastyczną. Rozkład ![]() na
na
![]() nazywamy stacjonarnym (niezmienniczym), jeśli
nazywamy stacjonarnym (niezmienniczym), jeśli ![]() (tzn.
dla wszystkich
(tzn.
dla wszystkich ![]() ,
, ![]() .
.
Rozkład stacjonarny ma następujące własności. Po pierwsze
zauważmy, że jeśli ![]() jest rozkładem stacjonarnym, to dla
każdego
jest rozkładem stacjonarnym, to dla
każdego ![]() ,
, ![]() (oczywista indukcja). Innymi słowy,
jeśli
(oczywista indukcja). Innymi słowy,
jeśli ![]() jest łańcuchem Markowa o macierzy przejścia
jest łańcuchem Markowa o macierzy przejścia ![]() i
rozkładzie początkowym
i
rozkładzie początkowym ![]() , to dla
, to dla ![]() , rozkład
, rozkład ![]() jest
równy
jest
równy ![]() . Można nawet powiedzieć więcej: dla wszystkich
. Można nawet powiedzieć więcej: dla wszystkich ![]() oraz dowolnego ciągu
oraz dowolnego ciągu ![]() (
(![]() również jest
dowolne) wektor
również jest
dowolne) wektor ![]() ma ten sam rozkład
co
ma ten sam rozkład
co ![]() . Istotnie,
. Istotnie,
co nie zależy od ![]() .
.
łańcuch o takiej własności nazywamy stacjonarnym.
Definicja 6.6
Okresem stanu ![]() nazywamy największą taką liczbę
nazywamy największą taką liczbę ![]() , że powrót
do stanu
, że powrót
do stanu ![]() jest możliwy tylko po liczbie kroków podzielnej przez
jest możliwy tylko po liczbie kroków podzielnej przez
![]() :
: ![]() NWD
NWD![]() .
.
Stan nazywamy okresowym jeśli ![]() i nieokresowym, jeśli
i nieokresowym, jeśli
![]() .
.
Stwierdzenie 6.5
W nieprzywiedlnym łańcuchu Markowa wszystkie stany mają ten sam okres.
Wobec tego następująca definicja ma sens.
Definicja 6.7
Nieprzywiedlny łańcuch Markowa ![]() nazywamy okresowym,
jeśli wszystkie jego stany mają okres większy niż
nazywamy okresowym,
jeśli wszystkie jego stany mają okres większy niż ![]() . W przeciwnym
razie łańcuch nazywamy nieokresowym.
. W przeciwnym
razie łańcuch nazywamy nieokresowym.
Lemat 6.1
łańcuch jest nieprzywiedlny i nieokresowy wtedy i tylko wtedy, gdy jest spełniony warunek
| (O) |
Dowód:
Oczywiście wystarczy tylko udowodnić implikację ![]() .
Ustalmy
.
Ustalmy ![]() oraz liczbę
oraz liczbę ![]() taką, że
taką, że ![]() .
Z definicji nieokresowości, istnieją liczby
względnie pierwsze
.
Z definicji nieokresowości, istnieją liczby
względnie pierwsze ![]() takie, że
takie, że
![]() ,
, ![]() . Jeśli
. Jeśli ![]() jest
dostatecznie duże, to
jest
dostatecznie duże, to
i mamy
Zatem
o ile ![]() jest dostatecznie duże.
jest dostatecznie duże.
Twierdzenie 6.5
Załóżmy, że warunek (O) jest spełniony i istnieje rozkład
stacjonarny ![]() . Wówczas każdy stan jest powracalny, rozkład stacjonarny
jest jednoznaczny oraz dla wszystkich
. Wówczas każdy stan jest powracalny, rozkład stacjonarny
jest jednoznaczny oraz dla wszystkich ![]() ,
,
Uwaga: Jak widać, przy założeniach twierdzenia,
![]() ,,przestaje zależeć od
,,przestaje zależeć od ![]() ” o ile
” o ile ![]() jest duże.
Innymi słowy, po dużej liczbie kroków łańcuch ,,zapomina”, z
jakiego stanu wystartował.
jest duże.
Innymi słowy, po dużej liczbie kroków łańcuch ,,zapomina”, z
jakiego stanu wystartował.
Dowód:
Dowód przeprowadzimy w pięciu krokach.
1. Wszystkie stany są albo powracalne, albo chwilowe. Załóżmy, że
ma miejsce ta druga możliwość. Liczba ![]() jest średnim czasem przebywania w stanie
jest średnim czasem przebywania w stanie ![]() przy
założeniu startowania ze stanu
przy
założeniu startowania ze stanu ![]() . Na mocy własności Markowa, mamy zatem
. Na mocy własności Markowa, mamy zatem
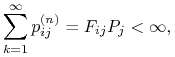 |
a zatem ![]() gdy
gdy ![]() . Z drugiej strony, dla
każdego
. Z drugiej strony, dla
każdego ![]() ,
,
i lewa strona dąży do ![]() na mocy tw. Lebesgue'a o zmajoryzowanym
przejściu do granicy. Stąd
na mocy tw. Lebesgue'a o zmajoryzowanym
przejściu do granicy. Stąd ![]() i sprzeczność.
i sprzeczność.
2. Rozważmy nową przestrzeń stanów ![]() oraz macierz przejścia
oraz macierz przejścia ![]() na tej przestrzeni, o wyrazach
na tej przestrzeni, o wyrazach
![]() (oczywiście jest to macierz
stochastyczna). Niech
(oczywiście jest to macierz
stochastyczna). Niech ![]() będzie rozkładem na
będzie rozkładem na ![]() : jest to rozkład stacjonarny dla
: jest to rozkład stacjonarny dla ![]() . Niech
. Niech
![]() będzie łańcuchem Markowa z tą macierzą
przejścia:
będzie łańcuchem Markowa z tą macierzą
przejścia: ![]() oraz
oraz ![]() to dwa niezależne łańcuchy
Markowa o macierzach przejścia
to dwa niezależne łańcuchy
Markowa o macierzach przejścia ![]() , startujące ze stanów
, startujące ze stanów ![]() ,
, ![]() ,
odpowiednio. Ponieważ będziemy zmieniać te punkty startowe, wygodnie
nam będzie pracować na miarach probabilistycznych
,
odpowiednio. Ponieważ będziemy zmieniać te punkty startowe, wygodnie
nam będzie pracować na miarach probabilistycznych
![]() . Jak łatwo sprawdzić, warunek (O)
jest spełniony; zatem na mocy kroku 1., z każdego stanu
. Jak łatwo sprawdzić, warunek (O)
jest spełniony; zatem na mocy kroku 1., z każdego stanu ![]() można dojść do każdego innego; w szczególności do stanu
można dojść do każdego innego; w szczególności do stanu ![]() .
Zatem dla wszystkich
.
Zatem dla wszystkich ![]() ,
, ![]() dla pewnego
dla pewnego
![]() .
.
3. Niech ![]() . Definiujemy
. Definiujemy
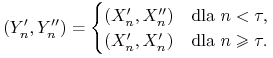 |
Z powyższej dyskusji wynika, że dla wszystkich ![]() ,
,
Sprawdzimy teraz, że ![]() ,
, ![]() są
łańcuchami Markowa (względem miary probabilistycznej
są
łańcuchami Markowa (względem miary probabilistycznej
![]() ) z macierzą przejścia
) z macierzą przejścia ![]() . Ograniczymy się tylko
do procesu
. Ograniczymy się tylko
do procesu ![]() ;w przypadku
;w przypadku ![]() przekształcenia są
analogiczne.
przekształcenia są
analogiczne.
i wystarczy obłożyć obie strony warunkową wartością oczekiwaną
względem ciągu ![]() .
.
4. Pokażemy, że dla ![]() ,
, ![]() . Mamy
. Mamy ![]() , więc
, więc
5. Mamy, dla wszystkich ![]() ,
, ![]() , skąd, na mocy poprzedniej części oraz
twierdzenia Lebesgue'a,
, skąd, na mocy poprzedniej części oraz
twierdzenia Lebesgue'a,
Jednoznaczność rozkładu stacjonarnego jest oczywista: ![]() jest
wyznaczony jako granice
jest
wyznaczony jako granice ![]() .
.
Na zakończenie zaprezentujemy następujący fakt. Dowodzi się go używając podobnej argumentacji jak w poprzednim twierdzeniu. Szczegóły pozostawiamy czytelnikowi.
Twierdzenie 6.6
Jeśli ![]() jest zbiorem skończonym i zachodzi warunek (O), to istnieje
rozkład stacjonarny i zachodzi teza poprzedniego twierdzenia.
jest zbiorem skończonym i zachodzi warunek (O), to istnieje
rozkład stacjonarny i zachodzi teza poprzedniego twierdzenia.
6.4. Zadania
1. Niech ![]() będzie pewnym zbiorem przeliczalnym.
Dany jest ciąg
będzie pewnym zbiorem przeliczalnym.
Dany jest ciąg ![]() niezależnych zmiennych losowych oraz ciąg
funkcyjny
niezależnych zmiennych losowych oraz ciąg
funkcyjny ![]() ,
, ![]() . Definiujemy ciąg
. Definiujemy ciąg
![]() wzorem
wzorem
gdzie ![]() jest pewną zmienną losową o wartościach w
jest pewną zmienną losową o wartościach w ![]() .
Dowieść, że
.
Dowieść, że ![]() jest łańcuchem Markowa.
jest łańcuchem Markowa.
2. Dany jest łańcuch Markowa ![]() na pewnej przestrzeni
na pewnej przestrzeni
![]() oraz różnowartościowa funkcja
oraz różnowartościowa funkcja ![]() . Wykazać, że
. Wykazać, że
![]() jest łańcuchem Markowa. Co jeśli
jest łańcuchem Markowa. Co jeśli ![]() nie jest
różnowartościowa?
nie jest
różnowartościowa?
3. Dany jest ciąg ![]() niezależnych zmiennych losowych o
tym samym rozkładzie
niezależnych zmiennych losowych o
tym samym rozkładzie ![]() . Rozstrzygnąć,
które z podanych niżej procesów są łańcuchami Markowa:
. Rozstrzygnąć,
które z podanych niżej procesów są łańcuchami Markowa:
4. Dany jest ciąg ![]() niezależnych zmiennych losowych o
tym samym rozkładzie
niezależnych zmiennych losowych o
tym samym rozkładzie ![]() ,
, ![]() . Niech
. Niech
![]() ,
, ![]() . Udowodnić, że ciągi
. Udowodnić, że ciągi
są łańcuchami Markowa.
5. Rzucamy kostką tak długo, aż pojawi się ciąg ![]() lub
lub
![]() . Jakie jest prawdopodobieństwo, że ciąg
. Jakie jest prawdopodobieństwo, że ciąg ![]() pojawi się
wcześniej?
pojawi się
wcześniej?
6. Rzucamy symetryczną monetą aż do momentu, gdy wyrzucimy
serię ![]() orłów. Obliczyć wartość oczekiwaną liczby
przeprowadzonych rzutów.
orłów. Obliczyć wartość oczekiwaną liczby
przeprowadzonych rzutów.
7. Macierz przejścia łańcucha Markowa ![]() na przestrzeni
na przestrzeni
![]() dana jest następująco:
dana jest następująco:
![\mathbb{P}=\left(\begin{array}[]{cccc}0&\frac{1}{2}&\frac{1}{2}&0\\
\frac{1}{4}&\frac{1}{2}&0&\frac{1}{4}\\
\frac{2}{3}&0&0&\frac{1}{3}\\
0&\frac{2}{3}&\frac{1}{3}&0\end{array}\right).](wyklady/rp2/mi/mi1091.png) |
-
a) Jakie jest prawdopodobieństwo dojścia w dwóch krokach ze stanu
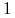 do stanu 2?
do stanu 2? -
b) Zakładając, że
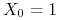 p.n.
obliczyć prawdopodobieństwo tego, że
p.n.
obliczyć prawdopodobieństwo tego, że
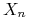 będzie w stanie 2 przed stanem 4.
będzie w stanie 2 przed stanem 4. -
c) Zakładając, że
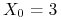 p.n.
obliczyć wartość oczekiwaną czasu dojścia do stanu 2.
p.n.
obliczyć wartość oczekiwaną czasu dojścia do stanu 2. -
d) Wyznaczyć rozkład stacjonarny. Czy łańcuch jest okresowy? Czy jest nieprzywiedlny?
8. Po wierzchołkach pięciokąta ABCDE porusza się pionek.
W chwili początkowej znajduje się w punkcie ![]() , a w każdym kolejnym ruchu
przesuwa się w sposób niezależny od poprzednich ruchów z
prawdopodobieństwem 1/2 do jednego z sąsiednich wierzchołków.
Obliczyć
, a w każdym kolejnym ruchu
przesuwa się w sposób niezależny od poprzednich ruchów z
prawdopodobieństwem 1/2 do jednego z sąsiednich wierzchołków.
Obliczyć
a) prawdopodobieństwo, że pionek powróci do punktu ![]() przed
dotarciem do punktu
przed
dotarciem do punktu ![]() ,
,
b) wartość oczekiwaną liczby ruchów, jakie wykona pionek przed
powrotem do punktu ![]() .
.
9. Naukowiec mający ![]() parasoli wędruje między domem a
biurem, zabierając ze sobą parasol (jeśli jest on pod ręką) wtedy,
gdy pada (prawdopodobieństwo
parasoli wędruje między domem a
biurem, zabierając ze sobą parasol (jeśli jest on pod ręką) wtedy,
gdy pada (prawdopodobieństwo ![]() ), lecz nie przy bezdeszczowej
pogodzie (prawdopodobieństwo
), lecz nie przy bezdeszczowej
pogodzie (prawdopodobieństwo ![]() ). Niech stanem łańcucha Markowa
będzie liczba parasoli znajdujących się pod ręką, bez względu na
to, czy naukowiec jest w domu, czy w miejscu pracy. Skonstruować
macierz przejścia i znaleźć rozkład stacjonarny. Znaleźć
przybliżone prawdopodobieństwo zmoknięcia naukowca w danym
(odległym) dniu, a następnie wykazać, że
). Niech stanem łańcucha Markowa
będzie liczba parasoli znajdujących się pod ręką, bez względu na
to, czy naukowiec jest w domu, czy w miejscu pracy. Skonstruować
macierz przejścia i znaleźć rozkład stacjonarny. Znaleźć
przybliżone prawdopodobieństwo zmoknięcia naukowca w danym
(odległym) dniu, a następnie wykazać, że ![]() parasoli jest w stanie
ochronić go w
parasoli jest w stanie
ochronić go w ![]() przed zmoknięciem (dla dowolnego
przed zmoknięciem (dla dowolnego ![]() ).
).
10. Proces ![]() jest łańcuchem Markowa.
jest łańcuchem Markowa.
(i) Czy dla dowolnego ![]() , liczb
, liczb ![]() oraz
stanów
oraz
stanów ![]() ,
, ![]() ,
, ![]() ,
, ![]() mamy
mamy
(ii) Czy dla dowolnego ![]() , liczb
, liczb ![]() oraz
zbiorów
oraz
zbiorów ![]() ,
, ![]() ,
, ![]() ,
, ![]() mamy
mamy
11. Dany jest łańcuch Markowa ![]() o macierzy przejścia
o macierzy przejścia ![]() ,
której każdy wiersz jest taki sam. Udowodnić, że zmienne
,
której każdy wiersz jest taki sam. Udowodnić, że zmienne ![]() ,
,
![]() ,
, ![]() są niezależne.
są niezależne.
12. Dany jest łańcuch Markowa ![]() startujący ze stanu
startujący ze stanu
![]() . Niech
. Niech ![]() . Udowodnić, że
. Udowodnić, że ![]() ma
rozkład geometryczny.
ma
rozkład geometryczny.
13. Rozważamy błądzenie losowe po ![]() : stan
: stan
![]() komunikuje się w jednym kroku z każdym ze
stanów
komunikuje się w jednym kroku z każdym ze
stanów ![]() ,
, ![]() z prawdopodobieństwem
z prawdopodobieństwem ![]() .
Udowodnić, że wszystkie stany są powracalne. Udowodnić, że nie
istnieje rozkład stacjonarny.
.
Udowodnić, że wszystkie stany są powracalne. Udowodnić, że nie
istnieje rozkład stacjonarny.
14. Niech ![]() będzie ustaloną liczbą dodatnią. Dany jest łańcuch Markowa na
będzie ustaloną liczbą dodatnią. Dany jest łańcuch Markowa na ![]() startujący z
startujący z ![]() , o następujących prawdopodobieństwach przejścia:
stan
, o następujących prawdopodobieństwach przejścia:
stan ![]() prowadzi w jednym kroku do
prowadzi w jednym kroku do ![]() z prawdopodobieństwem
z prawdopodobieństwem
![]() oraz do
oraz do ![]() z prawdopodobieństwem
z prawdopodobieństwem
![]() . Czy
łańcuch jest okresowy? Czy jest nieprzywiedlny? Dla jakich
. Czy
łańcuch jest okresowy? Czy jest nieprzywiedlny? Dla jakich ![]() łańcuch jest powracalny? Dla jakich
łańcuch jest powracalny? Dla jakich ![]() istnieje rozkład
stacjonarny?
istnieje rozkład
stacjonarny?
15. Dany jest spójny graf ![]() o skończonej liczbie
wierzchołków oraz łańcuch Markowa o
wartościach w
o skończonej liczbie
wierzchołków oraz łańcuch Markowa o
wartościach w ![]() taki, że z każdego wierzchołka
taki, że z każdego wierzchołka ![]() można w
jednym kroku dojść do jednego z wierzchołków sąsiadujących z
można w
jednym kroku dojść do jednego z wierzchołków sąsiadujących z ![]() .
Niech
.
Niech ![]() oznacza liczbę sąsiadów
oznacza liczbę sąsiadów ![]() . Udowodnić, że
. Udowodnić, że
![]() jest rozkładem stacjonarnym.
jest rozkładem stacjonarnym.
16. W modelu dyfuzji (przykład 5) powyżej) z ![]() ,
załóżmy, że w chwili
,
załóżmy, że w chwili ![]() nie ma żadnej cząstki w pojemniku I. Wyznaczyć
przybliżone prawdopodobieństwo tego, że w chwili
nie ma żadnej cząstki w pojemniku I. Wyznaczyć
przybliżone prawdopodobieństwo tego, że w chwili ![]() nie będzie
żadnej cząstki w I pojemniku.
nie będzie
żadnej cząstki w I pojemniku.




