Zagadnienia
3. Generowanie zmiennych losowych I. Ogólne metody
3.1. Przykłady
Moje wykłady ograniczają się do zagadnień leżących w kompetencji rachunku prawdopodobieństwa i statystyki. U podstaw symulacji stochastycznych leży generowanie ,,liczb pseudo-losowych”, naśladujących zachowanie zmiennych losowych o rozkładzie jednostajnym. Jak to się robi, co to jest ,,pseudo-losowość”, czym się różni od ,,prawdziwej losowości”? To są fascynujące pytania, którymi zajmuje się: teoria liczb, teoria (chaotycznych) układów dynamicznych oraz filozofia. Dyskusja na ten temat przekracza ramy tych wykładów. Z punktu widzenia użytkownika, ,,liczby losowe” są bardzo łatwo dostępne, bo ich generatory są wbudowane w systemy komputerowe. Przyjmę pragmatyczny punkt widzenia i zacznę od następującego założenia.
Założenie 3.1
Mamy do dyspozycji potencjalnie nieskończony ciąg
niezależnych zmiennych losowych ![]() o jednakowym rozkładzie
o jednakowym rozkładzie ![]() .
.
W języku algorytmicznym: przyjmujemy, że każdorazowe wykonanie instrukcji zapisanej w pseudokodzie
| Gen |
wygeneruje kolejną (nową) zmienną ![]() . Innymi słowy, zostanie wykonane nowe, niezależne
doświadczenie polegające na wylosowaniu przypadkowo wybranej liczby z przedziału
. Innymi słowy, zostanie wykonane nowe, niezależne
doświadczenie polegające na wylosowaniu przypadkowo wybranej liczby z przedziału
![]() .
.
Przykład 3.1
Wykonanie pseudokodu
| for |
| begin |
| Gen |
| write |
| end |
da, powiedzmy, taki efekt:
0.32240106 0.38971803 0.35222521 0.22550039 0.04162166
0.13976025 0.16943910 0.69482111 0.28812341 0.58138865
Nawiasem mówiąc, rzeczywisty kod w R, który wyprodukował nasze 10 liczb losowych był taki:
U <- runif(10);U
Język R jest zwięzły i piękny, ale nasz pseudokod ma pewne walory dydaktyczne.
Zajmiemy się teraz pytaniem, jak ,,wyprodukować” zmienne losowe o różnych rozkładach, wykorzystując zmienne ![]() .
W tym podrozdziale pokażę kilka przykładów, a w następnym przedstawię rzecz nieco bardziej systematycznie.
.
W tym podrozdziale pokażę kilka przykładów, a w następnym przedstawię rzecz nieco bardziej systematycznie.
Przykład 3.2 (Rozkład Wykładniczy)
To jest wyjątkowo łatwy do generowania rozkład – wystarczy taki algorytm:
| Gen |
Na wyjściu, ![]() . Żeby się o tym przekonać, wystarczy obliczyć dystrybuantę tej
zmiennej losowej:
. Żeby się o tym przekonać, wystarczy obliczyć dystrybuantę tej
zmiennej losowej:
![]() .
Jest to najprostszy przykład ogólnej metody ,,odwracania dystrybuanty”, której poświęcę następny
podrozdział.
.
Jest to najprostszy przykład ogólnej metody ,,odwracania dystrybuanty”, której poświęcę następny
podrozdział.
Przykład 3.3 (Generacja rozkładu normalnego)
Zmienna losowa
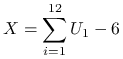 |
ma w przybliżeniu standardowy rozkład normalny ![]() . Wynika to
z Centralnego Twiedzenia Granicznego (jeśli uznamy, że liczba
. Wynika to
z Centralnego Twiedzenia Granicznego (jeśli uznamy, że liczba ![]() jest
dostatecznie bliska
jest
dostatecznie bliska ![]() ; zauważmy, że
; zauważmy, że ![]() i
i ![]() ). Oczywiście, w czasach szybkich komputerów
ta przybliżona metoda zdecydowanie nie jest polecana. Jest natomiast pouczające zbadać (symulacyjnie!) jak dobre jest przybliżenie. Faktycznie
bardzo trudno odróżnić próbkę
). Oczywiście, w czasach szybkich komputerów
ta przybliżona metoda zdecydowanie nie jest polecana. Jest natomiast pouczające zbadać (symulacyjnie!) jak dobre jest przybliżenie. Faktycznie
bardzo trudno odróżnić próbkę ![]() wyprodukowaną przez powyższy algorytm od próbki pochodzącej dokładnie z rozkłdu
wyprodukowaną przez powyższy algorytm od próbki pochodzącej dokładnie z rozkłdu
![]() (chyba, że
(chyba, że ![]() jest ogromne).
jest ogromne).
Przykład 3.4 (Algorytm Boxa-Müllera)
Oto, dla porównania, bardziej współczesna – i całkiem dokładna metoda generowania zmiennych o rozkładzie normalnym.
| Gen |
| Gen |
| Gen |
Na wyjściu obie zmienne ![]() i
i ![]() mają rozkład
mają rozkład ![]() i w dodatku są niezależne.
Uzasadnienie poprawności algorytmu Boxa-Müllera opiera się na dwu faktach: zmienna
i w dodatku są niezależne.
Uzasadnienie poprawności algorytmu Boxa-Müllera opiera się na dwu faktach: zmienna ![]() ma rozkład
ma rozkład
![]() , zaś kąt
, zaś kąt ![]() między osią i promieniem wodzącym punktu
między osią i promieniem wodzącym punktu ![]() ma
rozkład
ma
rozkład ![]() .
.
Ciekawe, że łatwiej jest generować zmienne losowe normalne ,,parami”.
Doświadczenie, polegające na wygenerowaniu zmiennych losowych ![]() i
i ![]() powtórzyłem
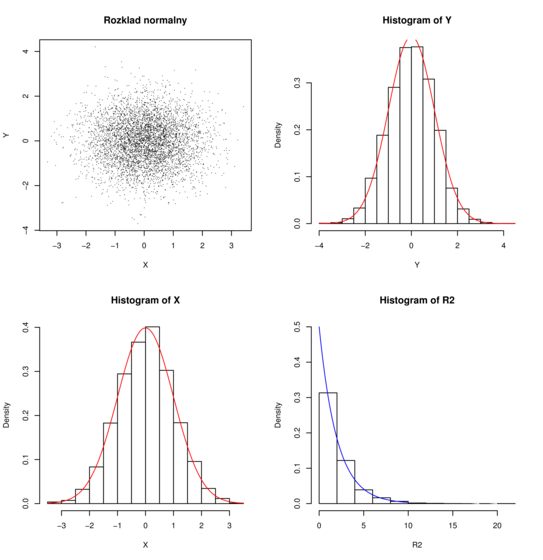
10000 razy. Na Rysunku 3.1 widać 10000 wylosowanych w ten sam sposób i niezależnie
punktów
powtórzyłem
10000 razy. Na Rysunku 3.1 widać 10000 wylosowanych w ten sam sposób i niezależnie
punktów ![]() , histogramy i gęstości brzegowe
, histogramy i gęstości brzegowe ![]() i
i ![]() (każda ze współrzędnych ma rozkłd
(każda ze współrzędnych ma rozkłd ![]() ) oraz histogram i gęstość
) oraz histogram i gęstość ![]() (
rozkład wykładniczy
(
rozkład wykładniczy ![]() ).
).
Histogram jest ,,empirycznym” (może w obecnym kontekście należałoby powiedzieć ,,symulacyjnym”) odpowiednikiem gęstości: spośród wylosowanych wyników zliczane są punkty należące do poszczególnych przedziałów.
Przykład 3.5 (Rozkład Poissona)
Algorytm przedstawiony niżej nie jest efektywny, ale jest prosty do zrozumienia.
| Gen |
| while |
| begin Gen |
Na wyjściu ![]() .
Istotnie, niech
.
Istotnie, niech ![]() będą i.i.d.
będą i.i.d. ![]() i
i
![]() . Wykorzystamy znany fakt, że
. Wykorzystamy znany fakt, że ![]() ma rozkład
ma rozkład
![]() .
Zmienne o rozkładzie wykładniczym przedstawiamy jako
.
Zmienne o rozkładzie wykładniczym przedstawiamy jako ![]() – patrz Przykład
3.2.
Zamiast dodawać zmienne
– patrz Przykład
3.2.
Zamiast dodawać zmienne ![]() możemy mnożyć zmienne
możemy mnożyć zmienne ![]() . Mamy
. Mamy
![]() , gdzie
, gdzie ![]() .
.
3.2. Metoda przekształceń
Zmienna losowa ![]() , która ma postać
, która ma postać
![]() , a więc jest pewną funkcją zmiennej
, a więc jest pewną funkcją zmiennej ![]() , w naturalny sposób ,,dziedziczy” rozkład prawdopodobieństwa
zgodnie z ogólnym schematem
, w naturalny sposób ,,dziedziczy” rozkład prawdopodobieństwa
zgodnie z ogólnym schematem ![]() (,,wykropkowany” argument jest zbiorem).
Przy tym zmienne
(,,wykropkowany” argument jest zbiorem).
Przy tym zmienne ![]() i
i ![]() nie muszą być jednowymiarowe. Jeśli obie zmienne mają ten sam wymiar i
przekształcenie
nie muszą być jednowymiarowe. Jeśli obie zmienne mają ten sam wymiar i
przekształcenie ![]() jest dyfeomorfizmem, to dobrze znany wzór wyraża gęstość rozkładu
jest dyfeomorfizmem, to dobrze znany wzór wyraża gęstość rozkładu ![]() przez gęstość
przez gęstość ![]() (Twierdzenie 5.1).
Odpowiednio dobierając funkcję
(Twierdzenie 5.1).
Odpowiednio dobierając funkcję ![]() możemy ,,przetwarzać” jedne rozkłady prawdopodobieństwa na inne, nowe.
możemy ,,przetwarzać” jedne rozkłady prawdopodobieństwa na inne, nowe.
Prawie wszystkie algorytmy generowania zmiennych losowych zawierają przekształcenia zmiennych losowych jako część składową. W niemal ,,czystej” postaci metoda przekształceń pojawiła się w algorytmie Boxa-Müllera, Przykładzie 3.4. Najważniejszym być może szczególnym przypadkiem metody przekształceń jest odwracanie dystrybuanty.
3.2.1. Odwrócenie dystrybuanty
Faktycznie, ta metoda została już wykorzystana w Przykładzie 3.2.
Opiera się ona na prostym fakcie. Jeżeli ![]() jest ciągłą i ściśle rosnącą dystrybuantą,
jest ciągłą i ściśle rosnącą dystrybuantą,
![]() i
i ![]() , to
, to ![]() .
Następująca definicja funkcji ,,pseudo-odwrotnej” pozwala
pozbyć się kłopotliwych założeń.
.
Następująca definicja funkcji ,,pseudo-odwrotnej” pozwala
pozbyć się kłopotliwych założeń.
Definicja 3.1
Jeżeli ![]() jest dowolną dystrybuantą, to funkcję
jest dowolną dystrybuantą, to funkcję ![]() określamy
wzorem:
określamy
wzorem:
Stwierdzenie 3.1
Nierówność ![]() jest równoważna
jest równoważna ![]() , dla dowolnych
, dla dowolnych ![]() i
i ![]() .
.
Dowód
Z prawostronnej ciągłości dystrybuanty ![]() wynika, że kres dolny w Definicji
3.1 jest osiągany, czyli
wynika, że kres dolny w Definicji
3.1 jest osiągany, czyli
Z drugiej strony,
po prostu dlatego, że ![]() . Teza stwierdzenia natychmiast wynika z dwóch
nierówności powyżej.
. Teza stwierdzenia natychmiast wynika z dwóch
nierówności powyżej.
Wniosek 3.1 (Ogólna metoda odwrócenia dystrybuanty)
Jeżeli ![]() i
i ![]() , to
, to ![]() . W skrócie,
. W skrócie, ![]() .
.
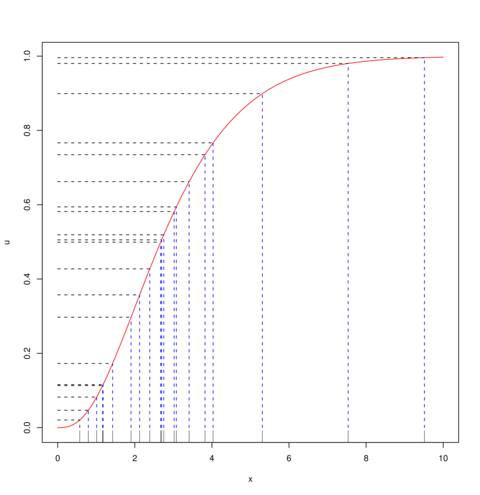
Na Rysunku 3.2 widać 20 punktów ![]() , które wylosowałem z rozkładu
, które wylosowałem z rozkładu ![]() (na osi pionowej) i odpowiadające im punkty
(na osi pionowej) i odpowiadające im punkty ![]() (na osi poziomej). W tym przypadku,
(na osi poziomej). W tym przypadku,
![]() jest dystrybuantą rozkładu
jest dystrybuantą rozkładu ![]() (linia krzywa). Najważniejszy fragment kodu w R jest taki:
(linia krzywa). Najważniejszy fragment kodu w R jest taki:
curve(pgamma(x,shape=3,rate=1), from=0,to=10) # rysowanie F U <- runif(20);X <- qgamma(U,shape=3,rate=1)
Zauważmy, że ta metoda działa również dla rozkładów dyskretnych i sprowadza się wtedy do metody ,,oczywistej”.
Przykład 3.6 (Rozkłady dyskretne)
Załóżmy, że ![]() dla
dla ![]() i
i ![]() .
Niech
.
Niech ![]() ,
, ![]() . Jeżeli
. Jeżeli ![]() jest dystrybuantą zmiennej
losowej
jest dystrybuantą zmiennej
losowej ![]() , to
, to
Odwracanie dystrybuanty ma ogromne znaczenie teoretyczne, bo jest całkowicie ogólną metodą generowania dowolnych zmiennych losowych jednowymiarowych. Może się to wydać dziwne, ale w praktyce ta metoda jest używana stosunkowo rzadko, z dwóch wzgłędów:
-
Obliczanie
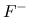 j bywa trudne i nieefektywne.
j bywa trudne i nieefektywne. -
Stosowalność metody ogranicza się do zmiennych losowych jednowymiarowych.
Podam dwa przykłady, w których zastosowanie metody odwracanie dystrybuanty jest rozsądne
Przykład 3.7 (Rozkład Weibulla)
Z definicji, ![]() , jeśli
, jeśli
dla ![]() . Odwrócenie dystrybuanty i generacja
. Odwrócenie dystrybuanty i generacja ![]() są łatwe:
są łatwe:
Przykład 3.8 (Rozkład Cauchy'ego)
Gęstość i dystrybuanta zmiennej ![]() są następujące:
są następujące:
Można tę zmienną generować korzystająć z wzoru:
3.3. Metoda eliminacji
To jest najważniejsza, najczęściej stosowana i najbardziej uniwersalna metoda. Zacznę od raczej oczywistego faktu, który jest w istocie probabilistycznym sformułowaniem definicji prawdopodobieństwa warunkowego.
Stwierdzenie 3.2
Przypuśćmy, że ![]() jest ciągiem niezależnych zmiennych losowych o
jednakowym rozkładzie, o wartościach w przestrzeni
jest ciągiem niezależnych zmiennych losowych o
jednakowym rozkładzie, o wartościach w przestrzeni ![]() . Niech
. Niech ![]() będzie
takim zbiorem, że
będzie
takim zbiorem, że ![]() . Niech
. Niech
Zmienne losowe ![]() i
i ![]() są niezależne, przy tym
są niezależne, przy tym
zaś
Dowód
Wystarczy zauważyć, że
W tym Stwierdzeniu ![]() może być dowolną przestrzenią mierzalną, zaś
może być dowolną przestrzenią mierzalną, zaś ![]() i
i ![]() – dowolnymi
zbiorami mierzalnymi. Stwierdzenie mówi po prostu, że prawdopodobieństwo warunkowe odpowiada
doświadczeniu losowemu powtarzanemu aż do momentu spełnienia warunku, przy
czym rezultaty poprzednich doświadczeń się ignoruje (stąd nazwa: eliminacja).
– dowolnymi
zbiorami mierzalnymi. Stwierdzenie mówi po prostu, że prawdopodobieństwo warunkowe odpowiada
doświadczeniu losowemu powtarzanemu aż do momentu spełnienia warunku, przy
czym rezultaty poprzednich doświadczeń się ignoruje (stąd nazwa: eliminacja).
3.3.1. Ogólny algorytm
Zakładamy, że umiemy generować zmienne losowe o gęstości ![]() , a chcielibyśmy
otrzymać zmienną o gęstości proporcjonalnej do funkcji
, a chcielibyśmy
otrzymać zmienną o gęstości proporcjonalnej do funkcji ![]() . Zakładamy, że
. Zakładamy, że ![]() .
.
| repeat |
| Gen |
| Gen |
| until |
Dowód poprawności algorytmu
Na mocy Stwierdzenia 3.2, zastosowanego do zmiennych losowych
![]() wystarczy pokazać, że
wystarczy pokazać, że
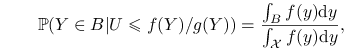 |
(3.1) |
gdzie ![]() jest przestrzenią wartości zmiennej losowej
jest przestrzenią wartości zmiennej losowej ![]() (i docelowej zmiennej losowej
(i docelowej zmiennej losowej ![]() ).
Warunkujemy teraz przez wartości zmiennej
).
Warunkujemy teraz przez wartości zmiennej ![]() , otrzymując
, otrzymując
Skorzystaliśmy z niezależności ![]() i
i ![]() oraz ze wzoru na prawdopodobieństwo całkowite. Otrzymaliśmy
licznik we wzorze (3.1). Mianownik dostaniemy zastępując
oraz ze wzoru na prawdopodobieństwo całkowite. Otrzymaliśmy
licznik we wzorze (3.1). Mianownik dostaniemy zastępując
![]() przez
przez ![]() .
.
Uwaga 3.1
Ważną zaletą algorytmu jest to, że nie trzeba znać ,,stałej normującej” gęstości ![]() , czyli
liczby
, czyli
liczby ![]() .
.
Uwaga 3.2
W istocie ![]() może być ogólną przestrzenią z miarą
może być ogólną przestrzenią z miarą ![]() . Żeby poczuć się pewniej
założę, że
. Żeby poczuć się pewniej
założę, że ![]() jest przestrzenią polską i miara
jest przestrzenią polską i miara ![]() jest
jest ![]() -skończona.
Możemy rozważać
gęstości i całki względem miary
-skończona.
Możemy rozważać
gęstości i całki względem miary ![]() – dowód poprawości algorytmu eliminacji
nie ulega zmianie. Nie widzę wielkiego sensu w przeładowaniu notacji,
można się umówić, że symbol
– dowód poprawości algorytmu eliminacji
nie ulega zmianie. Nie widzę wielkiego sensu w przeładowaniu notacji,
można się umówić, że symbol ![]() jest skrótem
jest skrótem ![]() .
Dociekliwy Czytelnik powinien zastanowić się, w jakiej sytuacji potrafi uzasadnić wszystkie
przejścia w dowodzie, powołując się na odpowiednie własności prawdopodobieństwa warunkowego
(np. twierdzenie o prawdopodobieństwie całkowitym itp.).
W każdym razie, algorytm eliminacji działa poprawnie, gdy
.
Dociekliwy Czytelnik powinien zastanowić się, w jakiej sytuacji potrafi uzasadnić wszystkie
przejścia w dowodzie, powołując się na odpowiednie własności prawdopodobieństwa warunkowego
(np. twierdzenie o prawdopodobieństwie całkowitym itp.).
W każdym razie, algorytm eliminacji działa poprawnie, gdy
-
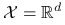 , gęstości są względem miary Lebesgue'a;
, gęstości są względem miary Lebesgue'a; -
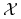 dyskretna, gęstości są względem miary liczącej.
dyskretna, gęstości są względem miary liczącej.
Uwaga 3.3
Efektywność algorytmu zależy od dobrania gęstości ![]() tak, aby majoryzowała funkcję
tak, aby majoryzowała funkcję ![]() ale nie
była dużo od niej większa.
Istotnie, liczba prób
ale nie
była dużo od niej większa.
Istotnie, liczba prób ![]() do zaakceptowania
do zaakceptowania ![]() ma rozkład geometryczny z
prawdopodobieństwem sukcesu
ma rozkład geometryczny z
prawdopodobieństwem sukcesu ![]() , zgodnie ze Stwierdzeniem 3.2,
zatem
, zgodnie ze Stwierdzeniem 3.2,
zatem ![]() . Iloraz
. Iloraz ![]() powinien być możliwie bliski jedynki, co jest możliwe jeśli
,,kształt funkcji
powinien być możliwie bliski jedynki, co jest możliwe jeśli
,,kształt funkcji ![]() jest podobny do
jest podobny do ![]() .
.
Zwykle metoda eliminacji stosuje się w połączeniu z odpowiednio dobranymi przekształceniami. Zilustrujmy to na poniższym przykładzie.
Przykład 3.9 (Rozkład Beta, algorytm Bermana)
Niech ![]() i
i ![]() będą niezależnymi zmiennymi losowymi o rozkładzie jednostajnym
będą niezależnymi zmiennymi losowymi o rozkładzie jednostajnym
![]() . Pod warunkiem, że
. Pod warunkiem, że ![]() zmienna losowa
zmienna losowa
![]() ma gęstość
ma gęstość ![]() proporcjonalną do funkcji
proporcjonalną do funkcji
![]() .
Zmienna losowa
.
Zmienna losowa ![]() ma gęstość
ma gęstość
![]() .
Zatem
.
Zatem ![]() ma rozkład
ma rozkład ![]() .
Algorytm jest więc następujący:
.
Algorytm jest więc następujący:
| repeat |
| Gen |
| |
| until |
| return |
Efektywność tego algorytmu jest tym większa, im mniejsze są parametry
![]() i
i ![]() (frakcja zakceptowanych
(frakcja zakceptowanych ![]() jest wtedy duża).
Dla ilustracji rozpatrzmy dwa przypadki.
jest wtedy duża).
Dla ilustracji rozpatrzmy dwa przypadki.
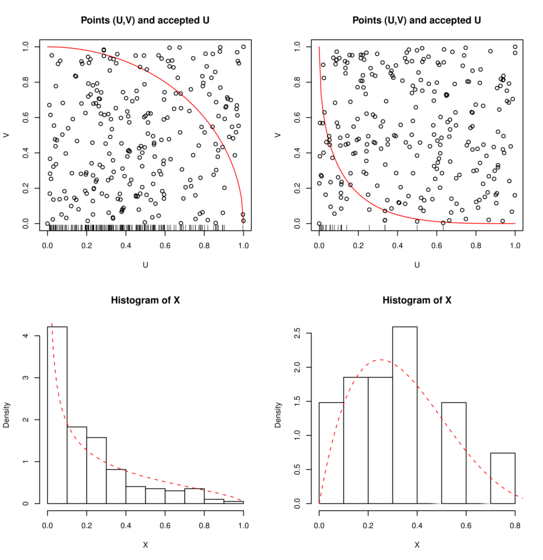
Na rysunku 3.3, po lewej stronie ![]() . Spośród
. Spośród ![]() punktów zaakceptowano
punktów zaakceptowano ![]() .
Przerywana krzywa jest wykresem gęstości rozkładu
.
Przerywana krzywa jest wykresem gęstości rozkładu ![]() .
Po prawej stronie
.
Po prawej stronie ![]() ,
, ![]() . Spośród
. Spośród ![]() punktów zaakceptowano tylko
punktów zaakceptowano tylko
![]() . Tym razem wykres pokazuje gęstość rozkładu
. Tym razem wykres pokazuje gęstość rozkładu ![]() .
Zaakceptowane punkty
.
Zaakceptowane punkty ![]() (o gęstości
(o gęstości ![]() ) są widoczne w postaci ,,kreseczek” na górnych rysunkach. Ciągłą linią jest narysowana
funkcja
) są widoczne w postaci ,,kreseczek” na górnych rysunkach. Ciągłą linią jest narysowana
funkcja ![]() .
.
3.3.2. Eliminacja w R
Zasadniczy algorytm eliminacji opisany w Stwierdzeniu 3.2 i w Punkcie 3.3.1 polega na powtarzaniu generacji
tak długo, aż zostanie spełnione kryterium akceptacji. Liczba prób jest losowa, a rezultatem jest jedna zmienna losowa o zadanym rozkładzie.
Specyfika języka R narzuca inny sposób przeprowadzania eliminacji. Działamy na wektorach, a więc od razu produkujemy ![]() niezależnych zmiennych
niezależnych zmiennych
![]() o rozkładzie
o rozkładzie ![]() , następnie poddajemy je wszystkie procedurze eliminacji. Przez sito eliminacji, powiedzmy
, następnie poddajemy je wszystkie procedurze eliminacji. Przez sito eliminacji, powiedzmy ![]() ,
przechodzi pewna część zmiennych. Otrzymujemy losową liczbę zmiennych o rozkładzie proporcjonalnym do
,
przechodzi pewna część zmiennych. Otrzymujemy losową liczbę zmiennych o rozkładzie proporcjonalnym do ![]() . Liczba zaakceptowanych zmiennych
ma oczywiście rozkład dwumianowy
. Liczba zaakceptowanych zmiennych
ma oczywiście rozkład dwumianowy ![]() z
z ![]() . To nie jest zbyt eleganckie.
W sztuczny sposób można zmusić R do wyprodukowania zadanej, nielosowej liczby zaakceptowanych zmiennych,
ale jeśli nie ma specjalnej konieczności, lepiej tego nie robić (przymus rzadko prowadzi do pozytywnych rezultatów).
. To nie jest zbyt eleganckie.
W sztuczny sposób można zmusić R do wyprodukowania zadanej, nielosowej liczby zaakceptowanych zmiennych,
ale jeśli nie ma specjalnej konieczności, lepiej tego nie robić (przymus rzadko prowadzi do pozytywnych rezultatów).
Dla przykładu, generowanie zmiennych ![]() o rozkładzie jesnostajnym na kole
o rozkładzie jesnostajnym na kole ![]() może w praktyce wyglądać tak:
może w praktyce wyglądać tak:
> n <- 1000 > X <- runif(n,min=-1,max=1) \# generowanie z rozkładu jednostajnego na [-1,1] > Y <- runif(n,min=-1,max=1) > Accept <- X^2+Y^2<1 \# wektor logiczny > X <- X[Accept] > Y <- Y[Accept]
Otrzymujemy pewną losową liczbę (około 785) punktów ![]() w kole jednostkowym.
w kole jednostkowym.
3.4. Metoda kompozycji
Jest to niezwykle prosta technika generowania zmiennych losowych. Załóżmy, że docelowy rozkład jest mieszanką prostszych rozkładów prawdopodobieństwa, czyli jego gęstość jest kombinacją wypukłą postaci
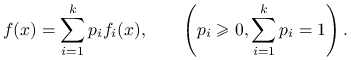 |
Jeśli umiemy losować z każdej gęstości ![]() to możemy uruchomić dwuetapowe losowanie:
to możemy uruchomić dwuetapowe losowanie:
| Gen |
| Gen |
| return |
Przykład 3.10 (Rozkład Laplace'a)
Rozkład Laplace'a (podwójny rozkład wykładniczy) ma gęstość
Można go ,,skomponować” z dwóch połówek rozkładu wykładniczego:
| Gen |
| Gen |
| if |
| return |