Zagadnienia

6.1 Stacjonarne procesy Gaussowskie
6.2 Procesy Poissona
- 6.2.1 Jednorodny proces Poissona na półprostej
- 6.2.2 Niejednorodne procesy Poissona w przestrzeni

6. Symulowanie procesów stochastycznych I.

Pełny tytuł tego rozdziału powinien brzmieć ,,Symulacje Niektórych Procesów Stochastycznych, Bardzo Subiektywnie Wybranych Spośród Mnóstwa Innych”. Nie będę szczegółowo tłumaczył, skąd pochodzi mój subiektywny wybór. Zrezygnowałem z próby przedstawienia procesów z czasem ciągłym i równocześnie ciągłą przestrzenią stanów, bo to temat oddzielny i obszerny.

6.1. Stacjonarne procesy Gaussowskie

Ograniczymy się do dwóch klas procesów, często używanych do modelowania różnych zjawisk. Będą to procesy z czasem dyskretnym i przestrzenią stanów $\mathbb{R}$ , to znaczy ciągi (zależnych) zmiennych losowych $X_{{0}},X_{{1}},\ldots,X_{{n}},\ldots$ o wartościach rzeczywistych. Niech $\ldots,W_{{-1}},W_{{0}},W_{{1}},\ldots,W_{{n}},\ldots$ będzie ciągiem niezależnych zmiennych losowych o jednakowym rozkładzie ${\rm N}(0,v^{{2}})$ (wygodnie posłużyć się tutaj ciągiem indeksowanym wszystkimi liczbami całkowitymi).

Definicja 6.1

Proces ruchomych średnich rzędu $q$ , w skrócie MA $(q)$ jest określony równaniem

$X_{{n}}=\beta _{1}W_{{n-1}}+\dots+\beta _{q}W_{{n-q}},\qquad(n=0,1,\ldots),$

gdzie $\beta _{1},\ldots,\beta _{q}$ jest ustalonym ciągiem współczynników.

Sposób generowania takiego procesu jest oczywisty i wynika wprost z definicji. Co więcej widać, że proces MA $(q)$ jest stacjonarny, to znaczy łączny rozkład prawdopodobieństwa zmiennych $X_{{0}},X_{{1}},\ldots,X_{{n}}$ jest taki sam jak zmiennych $X_{{k}},X_{{k+1}},\ldots,X_{{k+n-1}}$ , dla dowolnych $n$ i $k$ . Intuicyjnie, proces nie zmienia się po ,,przesunięciu czasu” o $k$ jednostek.

Definicja 6.2

Proces autoregresji rzędu $p$ , w skrócie AR $(p)$ jest określony równaniem rekurencyjnym

$X_{{n}}=\alpha _{1}X_{{n-1}}+\dots+\alpha _{p}X_{{n-p}}+W_{{n}},\qquad(n=p,p+1,\ldots),$

gdzie $\alpha _{1},\ldots,\alpha _{p}$ jest ustalonym ciągiem współczynników.

Procesy autoregresji wydają się bardzo odpowiednie do modelowania ,,szeregów czasowych”: stan układu w chwili $n$ zależy od stanów przeszłych i dotatkowo jeszcze od przypadku. Procesy AR $(1)$ , w szczególności są łańcuchami Markowa. Sposób generowania procesów AR $(p)$ jest też bezpośrednio widoczny z definicji. Pojawia się jednak pewien problem. Jak znaleźć $X_{{0}},\dots,X_{{p-1}}$ na początku algorytmu w taki sposób, żeby proces był stacjonarny? Jest to o tyle istotne, że rzeczywiste procesy (na przykład czeregi czasowe w zastosowaniach ekonomicznych) specjaliści uznają za stacjonarne, przynajmniej w przybliżeniu.

Rozważmy dla wygody oznaczeń podwójnie nieskończony proces

$\ldots,X_{{-1}},X_{{0}},X_{{1}},\ldots$

spełniający równanie autoregresji rzędu $p$ . Załóżmy, że ten proces jest stacjonarny i wektor $X_{{0}},\dots,X_{{p-1}}$ rozkład normalny, ${\rm N}(0,\Sigma)$ . Stacjonarność implikuje, że elementy macierzy $\Sigma$ muszą być postaci ${\rm Cov}(X_{i},X_{j})=\sigma^{2}\rho _{{i-j}}$ . Mamy przy tym $\rho _{{-k}}=\rho _{{k}}$ , co może być traktowane jako wygodna konwencja (po to właśnie ,,rozszerzamy” proces w obie strony). Zastosowanie równania definiującego autoregresję prowadzi do wniosku, że

$\begin{split}\sigma^{2}\rho _{k}&={\rm Cov}(X_{{0}},X_{{k}})={\rm Cov}(X_{{0}},\alpha _{1}X_{{k-1}}+\cdots+\alpha _{p}X_{{k-p}}+W_{{k}})\\ &=\sigma^{2}\alpha _{1}\rho _{{k-1}}+\sigma^{2}\alpha _{2}\rho _{{k-2}}+\cdots+\sigma^{2}\alpha _{p}\rho _{{k-p}}.\end{split}$

Podobnie,

$\begin{split}\sigma^{2}&={\rm Var}(X_{{0}})={\rm Cov}(X_{{0}},\alpha _{1}X_{{-1}}+\cdots+\alpha _{p}X_{{-p}}+W_{{0}})\\ &=\sigma^{2}\alpha _{1}\rho _{{1}}+\sigma^{2}\alpha _{2}\rho _{{2}}+\cdots+\sigma^{2}\alpha _{p}\rho _{{p}}+v^{2},\end{split}$

gdzie $v^{2}={\rm Var}(W_{0})$ . Otrzymujemy następujący układ równań na współczynniki autokorelacji $\rho _{k}$ :

$\qquad\left\{\begin{array}[]{ll}\rho _{1}=\alpha _{1}+\alpha _{2}\rho _{{1}}+\alpha _{3}\rho _{2}+\ldots+\alpha _{p}\rho _{{p-1}},\\ \rho _{2}=\alpha _{1}\rho _{1}+\alpha _{2}+\alpha _{3}\rho _{1}+\ldots+\alpha _{p}\rho _{{p-2}},\\ \dots,\\ \rho _{p}=\alpha _{1}\rho _{{p-1}}+\alpha _{2}\rho _{{p-2}}+\alpha _{3}\rho _{2}+\ldots+\alpha _{p},\\ \end{array}\right.$

(6.1)

Można pokazać, że ten ten układ ma rozwiązanie, jeśli wielomian charakterystyczny $A(z)=1-\alpha _{1}z-\ldots-\alpha _{p}z^{p}$ nie ma zer w kole $\{|z|\leq 1\}$ . Ponadto mamy równanie na wariancję stacjonarną:

$\qquad\sigma^{2}=\frac{v^{2}}{1-\rho _{1}\alpha _{1}-\ldots-\alpha _{p}\rho _{p}}$

(6.2)

Metoda generowania stacjonarnego procesu AR $(p)$ , $X_{{0}},X_{{1}},\ldots,X_{p},\ldots$ jest następująca. Znajdujemy rozwiązanie układu równań (6.1), wariancję obliczamy ze wzoru (6.2) i tworzymy macierz $\Sigma=(\sigma^{2}\rho _{{i-j}})_{{i,j=0,\ldots,p-1}}$ . Generujemy wektor losowy $(X_{{0}},X_{{1}},\ldots,X_{{p-1}})\sim{\rm N}(0,\Sigma)$ i dalej generujemy rekurencyjnie $X_{{p}},X_{{p+1}},\ldots$ używając równania autoregresji. Aby się przekonać, że tak generowany proces jest stacjonarny, wystarczy sprawdzić że identyczne są rozkłady wektorów $(X_{{0}},X_{{1}},\ldots,X_{{p-1}})$ i $(X_{{1}},X_{{2}},\ldots,X_{{p}})$ . Mamy

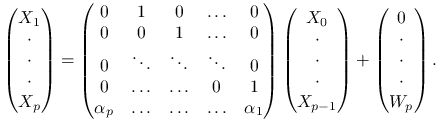$\begin{pmatrix}X_{{1}}\\ \cdot\\ \cdot\\ \cdot\\ X_{{p}}\\ \end{pmatrix}=\begin{pmatrix}0&1&0&\dots&0\\ 0&0&1&\dots&0\\ 0&\ddots&\ddots&\ddots&0\\ 0&\dots&\dots&0&1\\ \alpha _{p}&\dots&\dots&\dots&\alpha _{1}\\ \end{pmatrix}\begin{pmatrix}X_{{0}}\\ \cdot\\ \cdot\\ \cdot\\ X_{{p-1}}\\ \end{pmatrix}+\begin{pmatrix}0\\ \cdot\\ \cdot\\ \cdot\\ W_{{p}}\\ \end{pmatrix}.$

Niech $R$ oznacza ,,dużą macierz” w tym wzorze . Z własności wielowymiarowych rozkładów normalnych wynika, że wystarczy sprawdzić równość

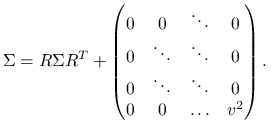$\Sigma=R\Sigma R^{T}+\begin{pmatrix}0&0&\ddots&0\\ 0&\ddots&\ddots&0\\ 0&\ddots&\ddots&0\\ 0&0&\dots&v^{2}\\ \end{pmatrix}.$

Macierz $\Sigma$ została tak wybrana, że ta równość jest spełniona.

6.2. Procesy Poissona

6.2.1. Jednorodny proces Poissona na półprostej

Definicja 6.3

Rozważmy niezależne zmienne losowe $W_{1},\ldots,W_{k},\ldots$ o jednakowym rozkładzie wykładniczym, $X_{{i}}\sim{\rm Ex}(\lambda)$ i utwórzmy kolejne sumy

$T_{0}=0,\; T_{1}=W_{1},\; T_{2}=W_{1}+W_{2},\;\ldots,\; T_{k}=W_{1}+\cdots+W_{k},\;\ldots$

Niech, dla $t\geq 0$ ,

$N(t)=\max\{ k:T_{k}\leq t\}.$

Rodzinę zmiennych losowych $N(t)$ nazywamy procesem Poissona.

Proces Poissona dobrze jest wyobrażać sobie jako losowy zbiór punktów na półprostej: $\{ T_{1},T_{2},\ldots,T_{k},\ldots\}$ . Zmienna $N(t)$ oznacza liczbę punktów, które ,,wpadły” w odcinek $]0,t]$ . Wygodnie będzie używać symbolu

$N(s,t)=N(t)-N(s)$

dla oznaczenia liczby punktów, które ,,wpadły” w odcinek $]s,t]$ .

Stwierdzenie 6.1

Jeśli $N(t)$ jest procesem Poissona, to

$\mathbb{P}(N(t)=k)=e^{{-\lambda t}}\frac{(\lambda t)^{k}}{k!}.$

Dowód

Zauważmy, że

$T_{k}\sim{\rm Gamma}(k,\lambda).$

Wobec tego ze wzoru na prawdopodobieństwo całkowite wynika, że

$\begin{split}\mathbb{P}(N(t)=k)&=\mathbb{P}(T_{k}\leq t,T_{{k+1}}>t)\\ &=\int _{0}^{t}\mathbb{P}(T_{{k+1}}>t|T_{k}=s)f_{{T_{k}}}(s)\;{\rm d}s\\ &=\int _{0}^{t}\mathbb{P}(W_{{k+1}}>t-s|T_{k}=s)f_{{T_{k}}}(s)\;{\rm d}s\\ &=\int _{0}^{t}{\rm e}^{{-\lambda(t-s)}}\frac{\lambda^{k}}{\Gamma(k)}s^{{k-1}}{\rm e}^{{-\lambda s}}{\rm d}s\\ &={\rm e}^{{-\lambda t}}\frac{\lambda^{k}}{\Gamma(k)}\int _{0}^{t}s^{{k-1}}{\rm d}s={\rm e}^{{-\lambda t}}\frac{\lambda^{k}}{(k-1)!}\frac{t^{k}}{k}={\rm e}^{{-\lambda t}}\frac{(\lambda t)^{k}}{k!}.\end{split}$

∎

Oczywiście $\mathbb{E}N(t)=\lambda t$ . Liczba

$\lambda=\frac{1}{\mathbb{E}W_{i}}=\frac{\mathbb{E}N(t)}{t}$

jest nazywana intensywnością procesu.

Stwierdzenie 6.2

Jeśli

$0<t_{1}<t_{2}<\cdots<t_{i}<\cdots,$

to zmienne losowe $N(t_{1}),N(t_{1},t_{2}),\ldots$ są niezależne i każda z nich ma rozkład Poissona:

$N(t_{{i-1}},t_{i})\sim{\rm Poiss}(\lambda(t_{i}-t_{{i-1}})).$

Dowód

Pokażemy, że warunkowo, dla $N(t_{1})=k$ , ciąg zmiennych losowych

$T_{{k+1}}-t_{1},W_{{k+2}},W_{{k+3}}\ldots,\quad\textrm{jest iid}\sim{\rm Ex}(\lambda).$

Wynika to z własności braku pamięci rozkładu wykładniczego. W istocie, dla ustalonych $N(t_{1})=k$ i $S_{k}=s$ mamy

$\begin{split}&\phantom{==}\mathbb{P}(T_{{k+1}}-t_{1}>t|N(t_{1})=k,T_{k}=s)\\ &=\mathbb{P}(T_{{k+1}}-t_{1}>t|T_{k}=s,T_{{k+1}}>t_{1})\\ &=\mathbb{P}(W_{{k+1}}>t_{1}+t-s|W_{{k+1}}>t_{1}-s)\\ &=\mathbb{P}(W_{{k+1}}>t)={\rm e}^{{-\lambda t}}.\end{split}$

Fakt, że zmienne $W_{{k+2}},W_{{k+3}}\ldots$ są niezależne od zdarzenia $N(t_{1})=k$ jest oczywisty. Pokazaliśmy w ten sposób, że losowy zbiór punktów $\{ T_{{k+1}}-t_{1},T_{{k+2}}-t_{1},\ldots\}$ ma (warunkowo, dla $N(t_{1})=k$ ) taki sam rozkład prawdopodobieństwa, jak $\{ T_{{1}},T_{{2}},\ldots\}$ . Proces Poissona obserwowany od momentu $t_{1}$ jest kopią wyjściowego procesu. Wynika stąd w szczególności, że zmienna losowa $N(t_{2},t_{1})$ jest niezależna od $N(t_{1})$ i $N(t_{2},t_{1})\sim{\rm Poiss}(\lambda(t_{2}-t_{1}))$ . Dalsza część dowodu przebiega analogicznie i ją pominiemy.

∎

Metoda generowania procesu Poisson oparta na Definicji 6.3 jest raczej oczywista. Zauważmy jednak, że nie jest to jedyna metoda. Inny sposób generowania (i inny sposób patrzenia na proces Poissona) jest związany z następującym faktem.

Stwierdzenie 6.3

Warunkowo, dla $N(t)=n$ , ciąg zmiennych losowych

$T_{1},\ldots,T_{n}$

ma rozkład taki sam, jak ciąg statystyk pozycyjnych

$U_{{1:n}},\ldots,U_{{n:n}}$

z rozkładu $U(0,t)$ .

Dowód

Z Wniosku 5.1 wynika, że warunkowo, dla $T_{n}=s$ ,

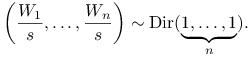$\left(\frac{W_{1}}{s},\ldots,\frac{W_{{n}}}{s}\right)\sim{\rm Dir}(\underbrace{1,\ldots,1}_{n}).$

Innymi słowy wektor losowy $(T_{1},\ldots,T_{{n-1}})$ ma taki rozkład, jak $n-1$ statystyk pozycyjnych z $U(0,s)$ .

Obliczmy warunkową gęstość zmiennej losowej ${T_{n}}$ , jeśli $N(t)=n$ :

$\begin{split} f_{{T_{n}}}(s|N(t)=n)&=\frac{\mathbb{P}(N(t)=n|T_{n}=s)f_{{T_{n}}}(s)}{\mathbb{P}(N(t)=n)}\\ &=\frac{\mathbb{P}(W_{{n+1}}>t-s)f_{{T_{n}}}(s)}{\mathbb{P}(N=n)}\\ &=\frac{{\rm e}^{{-\lambda(t-s)}}({\lambda^{n}}/{(n-1)!})s^{{n-1}}{\rm e}^{{-\lambda s}}}{{\rm e}^{{-\lambda t}}{(\lambda t)^{n}}/{n!}}\\ &=\frac{ns^{{n-1}}}{t^{n}}.\end{split}$

A zatem warunkowo, dla $N(t)=n$ , zmienna losowa ${T_{n}}/{t}$ ma rozklad ${\rm Beta}(n,1)$ i w konsekwencji (przypomnijmy sobie algorytm generowania zmiennych o rozkładzie Dirichleta)

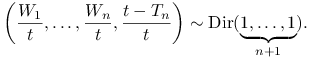$\left(\frac{W_{1}}{t},\ldots,\frac{W_{{n}}}{t},\frac{t-T_{n}}{t}\right)\sim{\rm Dir}(\underbrace{1,\ldots,1}_{{n+1}}).$

Innymi słowy wektor losowy $(T_{1},\ldots,T_{{n-1}},T_{n})$ ma taki rozkład, jak $n$ statystyk pozycyjnych z $U(0,t)$ .

∎

Wynika stąd następujący sposób generowania procesu Poissona na przedziale $[0,t]$ .

Gen $N\sim{\rm Poiss}(\lambda t)$

for $i=1$ to $N$ do Gen $U_{i}\sim{\rm U}(0,t)$ ;

Sort $(U_{1},\dots,U_{N})$

$(T_{1},\dots,T_{N}):=(U_{{1:N}},\dots,U_{{N:N}})$

Co ważniejsze, Stwierdzenia 6.1, 6.2 i 6.3 wskazują, jak powinny wyglądać uogólnienia procesu Poissona i jak generować takie ogólniejsze procesy. Zanim tym się zajmiemy, zróbmy dygresję i podajmy twierdzenie charakteryzujące ,,zwykły” proces Poissona. Nie jest ono bezpośrednio używane w symulacjach, ale wprowadza pewien ważny sposób określania procesów, który ułatwia zrozumienie łańcuchów Markowa z czasem ciągłym i jest bardzo użyteczny w probabilistycznym modelowaniu zjawisk.

Twierdzenie 6.1

Załóżmy, że $(N(t):t\geqslant 0)$ jest procesem o wartościach w $\{ 0,1,2,\ldots\}$ , stacjonarnych i niezależnych przyrostach (to znaczy $N(t)-N(s)$ jest niezależne od $(N(u),u\leq s)$ i ma rozkład zależny tylko od $t-s$ dla dowolnych $0<s<t$ ) oraz, że trajektorie $N(t)$ są prawostronnie ciągłymi funkcjami mającymi lewostronne granice (prawie na pewno). Jeżeli $N(0)=0$ i spełnione są następujące warunki:

$(i)\quad\lim _{{t\rightarrow 0}}\frac{\mathbb{P}(N(t)=1)}{t}=\lambda,$

$(ii)\quad\lim _{{t\rightarrow 0}}\frac{\mathbb{P}(N(t)\geq 2)}{t}=0,$

to $N(\cdot)$ jest jednorodnym procesem Poissona z intensywnością $\lambda$

Bardzo prosto można zauważyć, że proces Poissona $(N(t):t\geqslant 0)$ o intensywności $\lambda$ ma własności wymienione w Twierdzeniu 6.1. Ciekawe jest, że te własności w pełni charakteryzują proces Poissona.

Dowód Tw. 6.1 – szkic

Pokażemy tylko, że

$p_{n}(t):=\mathbb{P}(N(t)=n)={\rm e}^{{-\lambda t}}\frac{(\lambda t)^{n}}{n!}.$

Najpierw zajmiemy się funkcją $p_{0}(t)=\mathbb{P}(N(t)=0)$ . Z niezależności i jednorodności przyrostów wynika tożsamość

$p_{0}(t+h)=p_{0}(h)p_{0}(t).$

Stąd

$\frac{p_{0}(t+h)-p_{0}(t)}{h}=\frac{p_{0}(h)-1}{h}p_{0}(t)=\bigg[-\frac{p_{1}(h)}{h}-\frac{\sum _{{i=2}}^{{\infty}}p_{i}(h)}{h}\bigg]p_{0}(h).$

Przejdźmy do granicy z $h\to 0$ i skorzystajmy z własności (i) i (ii). Dostajemy proste równanie różniczkowe:

$p^{{\prime}}_{0}(t)=-\lambda p_{0}(t).$

Rozwiązanie tego równania z warunkiem początkowym $p_{0}(0)=1$ jest funkcja

$p_{0}(t)={\rm e}^{{-\lambda t}}.$

Bardzo podobnie obliczamy kolejne funkcje $p_{n}$ . Postępujemy rekurencyjnie: zakładamy, że znamy $p_{{n-1}}$ i układamy równanie różniczkowe dla funkcji $p_{{n}}$ . Podobnie jak poprzednio,

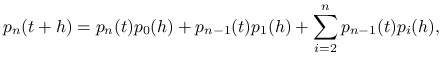$p_{n}(t+h)=p_{n}(t)p_{0}(h)+p_{{n-1}}(t)p_{1}(h)+\sum _{{i=2}}^{n}p_{{n-1}}(t)p_{i}(h),$

a zatem

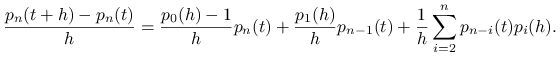$\frac{p_{n}(t+h)-p_{n}(t)}{h}=\frac{p_{0}(h)-1}{h}p_{n}(t)+\frac{p_{1}(h)}{h}p_{{n-1}}(t)+\frac{1}{h}\sum _{{i=2}}^{n}p_{{n-i}}(t)p_{i}(h).$

Korzystając z własności (i) i (ii) otrzymujemy równanie

$p_{n}^{{\prime}}(t)=-\lambda p_{n}(t)+\lambda p_{{n-1}}(t).$

To równanie można rozwiązać metodą uzmiennienia stałej: poszukujemy rozwiązania postaci $p_{n}(t)=c(t){\rm e}^{{-\lambda t}}$ . Zakładamy przy tym indukcyjnie, że $p_{{n-1}}(t)=(\lambda t)^{{n-1}}{\rm e}^{{-\lambda t}}/(n-1)!$ i mamy oczywisty warunek początkowy $p_{n}(0)=0$ . Stąd już łatwo dostać dowodzony wzór na $p_{n}$ .

Na koniec zauważmy, że z postaci funkcji $p_{0}$ łatwo wywnioskować jaki ma rozkład zmienna $T_{1}=\inf\{ t:N(t)>0\}$ . Istotnie, $\mathbb{P}(T_{1}>t)=\mathbb{P}(N(t)=0)$ $=p_{0}(t)={\rm e}^{{-\lambda t}}$ .

∎

Własności (i) i (ii), w połączeniu z jednorodnością przyrostów można przepisać w następującej sugestywnej formie:

$\quad\begin{split}&\mathbb{P}(N(t+h)=n+1|N(t)=n)=\lambda h+o(h),\\ &\mathbb{P}(N(t+h)=n|N(t)=n)=1-\lambda h+o(h),\quad h\searrow 0.\end{split}$

(6.3)

Jest to o tyle ważne, że w podobnym języku łatwo formułować założenia o ogólniejszych procesach, na przykład tak zwanych procesach urodzin i śmierci. Wrócimy do tego przy okazji omawiania łańcuchów Markowa.

6.2.2. Niejednorodne procesy Poissona w przestrzeni

Naturalne uogólnienia procesu Poissona polegają na tym, że rozważa się losowe zbiory punktów w przestrzeni o dowolnym wymiarze i dopuszcza się różną intensywność pojawiania się punktów w różnych rejonach przestrzeni. Niech ${\cal X}$ będzie przestrzenią polską. Czytelnik, który nie lubi abstrakcji może założyć, że ${\cal X}\subseteq\mathbb{R}^{{d}}$ .

Musimy najpierw wprowadzić odpowiednie oznaczenia. Rozważmy ciąg wektorów losowych w ${\cal X}$ :

$X_{1},\ldots,X_{n},\ldots$

(może to być ciag skonczony lub nie, liczba tych wektorów może być zmienną losową). Niech, dla $A\subseteq{\cal X}$ ,

$N(A)=\#\{ i:X_{i}\in A\}$

oznacza liczbę wektorów, które ,,wpadły do zbioru $A$ ” (przy tym dopuszczamy wartość $N(A)=\infty$ i umawiamy się liczyć powtarzające się wektory tyle razy, ile razy występują w ciągu).

Niech teraz $\mu$ będzie miarą na ( $\sigma$ -ciele borelowskich podzbiorów) przestrzeni ${\cal X}$ .

Definicja 6.4

$N(\cdot)$ jest procesem Poissona z miara intensywnosci $\mu$ , jesli

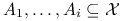dla parami rozłącznych zbiorów $A_{1},\ldots,A_{i}\subseteq{\cal X}$ , odpowiadające im zmienne losowe $N(A_{1}),\ldots,N(A_{i})$ są niezależne;
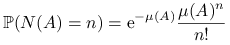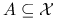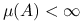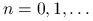$\displaystyle\mathbb{P}(N(A)=n)={\rm e}^{{-\mu(A)}}\frac{\mu(A)^{n}}{n!}$ , dla każdego $A\subseteq{\cal X}$ takiego, że $\mu(A)<\infty$ i dla $n=0,1,\ldots$ .

Z elementarnych własności rozkładu Poissona wynika następujący wniosek.

Wniosek 6.1

Rozważymy rozbicie zbioru $A$ o skończonej mierze intensywności, $\mu(A)<\infty$ , na rozłączną sumę $A=A_{1}\cup\cdots\cup A_{k}$ . Wtedy

$\begin{split}&\mathbb{P}\left(N(A_{1})=n_{1},\ldots,N(A_{k})=n_{k}|N(A)=n\right)\\ &\qquad\qquad=\frac{n!}{n_{1}!\cdots n_{k}!}\mu(A_{1})^{{n_{1}}}\cdots\mu(A_{k})^{{n_{k}}},\qquad(n_{1}+\cdots+n_{k}=n).\end{split}$

Jeśli natomiast $\mu(A)=\infty$ to łatwo zauważyć, że $N(A)=\infty$ z prawdopodobieństwem 1.

Z Definicji 6.4 i Wniosku 6.1 natychmiast wynika następujący algorytm generowania procesu Poissona. Załóżmy, że interesuje nas ,,fragment” procesu w zbiorze $A\subseteq{\cal X}$ o skończonej mierze intensywności. W praktyce zawsze symulacje muszą się do takiego fragmentu ograniczać. Zauważmy, że unormowana miara $\mu(\cdot)/\mu(A)$ jest rozkładem prawdopodobieństwa (zmienna losowa $X$ ma ten rozkład, jeśli $\mathbb{P}(X\in B)=\mu(B)/\mu(A)$ , dla $B\subseteq A$ ).

Gen $N\sim{\rm Poiss}(\mu(A))$

for $i=1$ to $N$ do Gen $X_{i}\sim\mu(\cdot)/\mu(A)$

Należy rozumieć, że formalnie definiujemy $N(B)=\#\{ i:X_{i}\in B\}$ dla $B\subseteq A$ , w istocie jednak za realizację procesu uważamy zbiór punktów $\{ X_{{1}},\ldots,X_{{N}}\}\subset A$ (,,zapominamy” o uporządkowaniu punktów). Widać, że to jest proste uogólnienie analogicznego algorytmu dla ,,zwykłego” procesu Poissona, podanego wcześniej.

Można również rozbić zbiór $A$ na rozłączną sumę $A=A_{1}\cup\cdots\cup A_{k}$ i generować niezależnie fragmenty procesu w każdej części $A_{{j}}$ .

Przykład 6.1

Jednorodny proces Poissona na kole $B^{{2}}=\{ x^{{2}}+y^{{2}}\leqslant 1\}$ można wygenerować w następujący sposób. Powiedzmy, że intensywność (punktów na jednostkę pola) jest $\lambda$ , to znaczy $\mu(B)=\lambda|B|$ , gdzie $|B|$ jest polem (miarą Lebesgue'a) zbioru $B$ .

Najpierw generujemy $N\sim{\rm Poiss}(\lambda\pi)$ , następnie punkty $(X_{{1}},Y_{{1}}),\ldots,(X_{{N}},Y_{{N}})$ niezależnie z rozkładu ${\rm U}(B^{{2}})$ . To wszystko.

Ciekawszy jest następny przykład.

Przykład 6.2 (Jednorodny proces Poissona w przestrzeni prostych)

Rys. 6.1. Proces Poissona w przestrzeni prostych.

Prostą na płaszczyźnie można sparametryzować podając kąt $\varphi\in[0,2\pi[$ jako tworzy prostopadła do prostej z osią poziomą oraz odległość $r\geq 0$ prostej od początku układu. Każda prosta jest więc opisana przez parę liczb $(\varphi,r)$ czyli punkt przestrzeni ${\cal L}=[0,2\pi[\times[0,\infty[$ . Jeśli teraz wygenerujemy jednorodny proces Poissona na tej przestrzeni, to znaczy proces o intensywności $\mu(B)=\lambda|B|$ , $B\subseteq{\cal L}$ , to można się spodziewać zbioru ,,losowo położonych prostych”. To widać na Rysunku 6.1. W istocie, wybór parametryzacji zapewnia, że rozkład prawdopodobieństwa procesu nie zależy od wyboru układu współrzędnych. Dowód, czy nawet precyzyjne sformułowanie tego stwierdzenia przekracza ramy tego skryptu. Intuicyjnie chodzi o to, że na obrazku ,,nie ma wyróżnionego kierunku ani wyróżnionego punktu”. Nie można sensownie zdefiniować pojęcia ,,losowej prostej” ale każdy przyzna, że proces Poissona o którym mowa można uznać za uściślenie intuicyjnie rozumianego pojęcia ,,losowego zbioru prostych”.

Ciekawe, że podstawowe metody generowania zmiennych losowych mają swoje odpowiedniki dla procesów Poissona. Rolę rozkładu prawdopodobieństwa przejnuje miara intensywności.

Przykład 6.3 (Odwracanie dystrybuanty)

Dla miary intensywności $\lambda$ na przestrzeni jednowymiarowej można zdefiniować dystrybuantę tej miary. Dla uproszczenia rozważmy przestrzeń ${\cal X}=[0,\infty[$ i założymy, że każdy zbiór ograniczony ma miarę skończoną. Niech $\Lambda(t)=\lambda([0,t])$ . Funkcję $\Lambda:[0,\infty[\to[0,\infty[$ nazwiemy dystrybuantą. Jest ona niemalejąca, prawostronnie ciągła, ale granica w nieskończoności $\Lambda(\infty)=\lim _{{x\to\infty}}\Lambda(x)$ może być dowolnym elementem z $[0,\infty]$ . Dla procesu Poissona na $[0,\infty[$ wygodnie wrócić do prostszych oznaczeń, pisząc $N(t)=N([0,t])$ jak we wcześniej rozpatrywanym przypadku jednorodnym.

Niech $J(t)$ będzie jednorodnym procesem Poissona na $[0,\infty[$ z intensywnoscia równą 1. Wtedy

$N(t)=J(\Lambda(t))$

jest niejednorodnym procesem Poissona z miarą intensywności $\lambda$ . W istocie, jeśli $0<t_{{1}}<t_{{2}}<\cdots$ to $N(t_{1}),N(t_{2})-N(t_{1}),\ldots$ są niezależne i maja rozkłady odpowiednio ${\rm Poiss}(\Lambda(t_{1})),{\rm Poiss}(\Lambda(t_{2})-\Lambda(t_{1})),\ldots$ . Zauważmy, że jeśli $R_{{1}}<R_{{2}}<\cdots$ oznaczają punkty skoku procesu $J(\cdot)$ to $N(t)=\max\{ k:R_{{k}}\leqslant\Lambda(t)\}=\max\{ k:\Lambda^{{-}}(R_{{k}})\leqslant t\}$ , gdzie $\Lambda^{{-}}$ jest uogólnioną funkcją odwrotną do dystrybuanty. Wobec tego punktami skoku procesu $N$ są $T_{{k}}=\Lambda^{{-}}(R_{{k}})$ . Algorytm jest taki:

Gen $N\sim{\rm Poiss}(\Lambda(t))$ ;

for $i:=1$ to $N$ do Gen $R_{{i}}\sim{\rm U}(0,\Lambda(t));\quad T_{i}:=\Lambda^{{-}}(R_{{i}})$

Pominęliśmy tu sortowanie skoków i założyliśmy, że symulacje ograniczamy do odcinka $[0,t]$ .

Przykład 6.4 (Przerzedzanie)

To jest odpowiednik metody eliminacji. Załóżmy, że mamy dwie miary intensywności: $\mu$ o gęstości $m$ i $\lambda$ o gęstości $l$ . To znaczy, że $\lambda(B)=\int _{{B}}l(x){\rm d}x$ i $\mu(B)=\int _{{B}}m(x){\rm d}x$ dla dowolnego zbioru $B\subseteq{\cal X}$ . Załóżmy, że $l(x)\leqslant m(x)$ i przypuśćmy, że umiemy generować proces Poissona o intensywności $\mu$ . Niech $X_{{1}},\ldots,X_{{N}}$ będą punktami tego procesu w zborze $A$ o skończonej mierze $\mu$ (wiemy, że $N\sim{\rm Poiss}(\mu(A)$ ). Punkt $X_{i}$ akceptujemy z prawdopodobieństwem $l(X_{i})/m(X_{i})$ (pozostawiamy w zbiorze) lub odrzucamy (usuwamy ze zbioru) z prawdopodobieństwem $1-l(X_{i})/m(X_{i})$ . Liczba pozostawionych punktów $L$ ma rozkład ${\rm Poiss}(\lambda(A))$ , zaś każdy z tych punktów ma rozkład o gęstości $l(x)/\lambda(A)$ , gdzie $\lambda(A)=\int _{{A}}l(x){\rm d}x$ . Te punkty tworzą proces Poissona z miarą intensywności $\lambda$ .

Gen $\mathbb{X}=\{ X_{{1}},\ldots,X_{{N}}\}\sim{\rm Poiss}(\mu(\cdot))$ ;

for $i:=1$ to $N$ Gen $U_{{i}}\sim{\rm U}(0,1)$ ;

if $U_{i}>l(X_{{i}})/m(X_{{i}})$ then $\mathbb{X}:=\mathbb{X}\setminus X_{{i}}$ ;

return $\mathbb{X}=\{ X_{{1}}^{\prime},\ldots,X_{{L}}^{\prime}\}\sim{\rm Poiss}(\lambda(\cdot))$

Przykład 6.5 (Superpozycja)

To jest z kolei odpowiednik metody kompozycji. Metoda opiera się na następującym prostym fakcie. Jezeli $N_{1}(\cdot),\ldots,N_{k}(\cdot)$ są niezależnymi procesami Poissona z miarami intensywnosci odpowiednio $\mu _{1}(\cdot),\ldots,\mu _{k}(\cdot)$ , to $N(\cdot)=\sum _{i}N_{i}(\cdot)$ jest procesem Poissona z intensywnością $\mu(\cdot)=\sum _{i}\mu _{i}(\cdot)$ . Dodawanie należy tu rozumieć w dosłaowny sposób, to znaczy $N(A)$ jest określone jako $\sum _{i}N_{i}(A)$ dla każdego zbioru $A$ . Jeśli utożsamimy procesy z losowymi zbiorami punktów to odpowiada temu operacja brania sumy mnogościowej (złączenia zbiorów). Niech $X_{{j,1}},\ldots,X_{{j,N_{j}}}$ będą punktami $j$ -tego procesu w zborze $A$ o skończonej mierze $\mu _{j}$ .

$\mathbb{X}=\emptyset$ ;

for $j:=1$ to $k$ do

begin

Gen $\mathbb{X}_{{j}}=\{ X_{{j,1}},\ldots,X_{{j,N_{{j}}}}\}\sim{\rm Poiss}(\mu _{{j}}(\cdot))$ ;

$\mathbb{X}:=\mathbb{X}\cup\mathbb{X}_{{j}}$ ;

end

return $\mathbb{X}=\{ X_{{1}}^{\prime},\ldots,X_{{N}}^{\prime}\}\sim{\rm Poiss}(\mu(\cdot))$

{ mamy tu $N=\sum _{j}N_{j}$ }

Wygodnie jest utożsamiać procesy Poissona z losowymi zbiorami punktów, jak uczyniliśmy w ostatnich przykładach (i mniej jawnie w wielu miejscach wcześniej). Te zbiory można rozumieć w zwykłym sensie, dodawać, odejmować tak jak w teorii mnogości pod warunkiem, że ich elementy się nie powtarzają. W praktyce mamy najczęściej do czynienia z intensywnościami, które mają gęstości ,,w zwykłym sensie”, czyli względem miary Lebesgue'a. Wtedy, z prawdopodobieństwem 1, punkty procesu Poissona nie powtarzają się.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Symulacje stochastyczne i metody Monte Carlo

Zagadnienia

6. Symulowanie procesów stochastycznych I.

6.1. Stacjonarne procesy Gaussowskie

Definicja 6.1

Definicja 6.2

6.2. Procesy Poissona

6.2.1. Jednorodny proces Poissona na półprostej

Definicja 6.3

Stwierdzenie 6.1

Dowód

Stwierdzenie 6.2

Dowód

Stwierdzenie 6.3

Dowód

Twierdzenie 6.1

Dowód Tw. 6.1 – szkic

6.2.2. Niejednorodne procesy Poissona w przestrzeni

Definicja 6.4

Wniosek 6.1

Przykład 6.1

Przykład 6.2 (Jednorodny proces Poissona w przestrzeni prostych)

Przykład 6.3 (Odwracanie dystrybuanty)

Przykład 6.4 (Przerzedzanie)

Przykład 6.5 (Superpozycja)