Zagadnienia

9.1 Losowanie warstwowe
9.2 Zmienne kontrolne
9.3 Zmienne antytetyczne

9. Algorytmy Monte Carlo II. Redukcja wariancji

W tym rozdziale omówię niektóre metody redukcji wariancji dla klasycznych algorytmów Monte Carlo, w których losujemy próbki niezależnie, z jednakowego rozkładu. Wiemy, że dla takich algorytmów wariancja estymatora zachowuje się jak ${\rm const}/n$ . Jedyne, co możemy zrobić – to konstruować takie algorytmy, dla których stała ,, ${\rm const}$ ” jest możliwie mała. Najważniejszą z tych metod faktycznie już poznaliśmy: jest to losowanie istotne, omówione w Rozdziale 8. Odpowiedni wybór ,,rozkładu instrumentalnego” może zmniejszyć wariancję…setki tysięcy razy! Istnieje jeszcze kilka innych, bardzo skutecznych technik. Do podstawowych należą: losowanie warstwowe, metoda zmiennych kontrolnych, metoda zmiennych antytetycznych. Możliwe są niezliczone modyfikacje i kombinacje tych metod. Materiał zawarty w tym rozdziale jest w dużym stopniu zaczerpnięty z monografii Ripleya [18].

9.1. Losowanie warstwowe

Tak jak w poprzednim rozdziale, zedanie polega na obliczeniu wielkości

$\theta=\mathbb{E}_{\pi}f(X)=\int _{{{\cal X}}}f(x)\pi(x){\rm d}x,$

(9.1)

gdzie rozkład prawdopodobieństwa i jego gęstość dla uproszczenia oznaczamy tym samym symbolem $\pi$ . Losowanie warstwowe polega na tym, że rozbijamy przestrzeń $X$ na sumę $k$ rozłącznych podzbiorów (warstw),

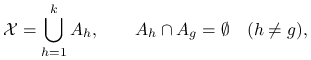${\cal X}=\bigcup _{{h=1}}^{k}A_{h},\qquad A_{h}\cap A_{g}=\emptyset\quad(h\not=g),$

(9.2)

i losujemy $k$ niezależnych próbek, po jednej z każdej warstwy. Niech $\pi _{h}$ będzie gęstostością rozkładu warunkowego zmiennej $X$ przy $X\in A_{h}$ , czyli

$\pi _{h}(x)=\frac{\pi(x)}{p_{h}}\mathbb{I}(x\in A_{h}),\qquad\text{gdzie}\quad p_{h}=\pi(A_{h})=\int _{{A_{h}}}\pi(x){\rm d}x.$

(9.3)

Widać natychmiast, że $\int _{B}\pi _{h}(x){\rm d}x=\pi(X\in B|X\in A_{h})$ . Rozbijamy teraz całkę, którą chcemy obliczyć:

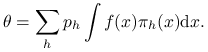$\theta=\sum _{{h}}p_{h}\int f(x)\pi _{h}(x){\rm d}x.$

(9.4)

Możemy użyć następującego estymatora warstwowego:

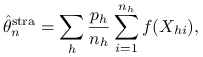${\hat{\theta}_{{n}}}^{{\rm stra}}=\sum _{{h}}\frac{p_{h}}{n_{h}}\sum _{{i=1}}^{{n_{h}}}f(X_{{hi}}),$

(9.5)

gdzie

$X_{{h1}},\ldots,X_{{hn_{h}}}\sim _{{\rm i.i.d}}\pi _{h},$

(9.6)

jest próbką rozmiaru $n_{h}$ wylosowaną z $h$ -tej warstwy ( $h=1,\ldots,k$ ). Jest to estymator nieobciążony,

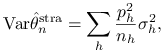${\rm Var}{\hat{\theta}_{{n}}}^{{\rm stra}}=\sum _{{h}}\frac{p_{h}^{2}}{n_{h}}\sigma _{h}^{2},$

(9.7)

gdzie $\sigma _{h}^{2}={\rm Var}_{\pi}(f(X)|x\in A_{h})$ .

Porównajmy estymator warstwowy (9.5) ze ,,zwykłym” estymatorem

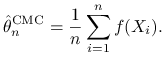${\hat{\theta}_{{n}}}^{{\rm CMC}}=\frac{1}{n}\sum _{{i=1}}^{{n}}f(X_{{i}}).$

(9.8)

opartym na jednej próbce

$X_{{1}},\ldots,X_{{n}}\sim _{{\rm i.i.d}}\pi.$

(9.9)

Oczywiście

${\rm Var}{\hat{\theta}_{{n}}}^{{\rm CMC}}=\frac{1}{n}\sigma^{2},$

(9.10)

gdzie $\sigma^{2}={\rm Var}_{\pi}f(X)$ . Żeby porównanie było ,,uczciwe” rozważmy próbkę liczności $n=\sum _{h}n_{h}$ . Jeśli decydujemy się na sumaryczną liczność próbki $n$ , to możemy w różny sposób ,,rozdzielić” to $n$ pomiędzy warstwami. To się nazywa alokacja próbki.

Stwierdzenie 9.1 (Alokacja proporcjonalna)

Jeżeli $n_{h}=p_{h}n$ dla $n=1,\ldots,k$ , to

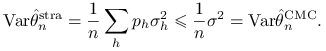${\rm Var}{\hat{\theta}_{{n}}}^{{\rm stra}}=\frac{1}{n}\sum _{{h}}{p_{h}}\sigma _{h}^{2}\leq\frac{1}{n}\sigma^{2}={\rm Var}{\hat{\theta}_{{n}}}^{{\rm CMC}}.$

(9.11)

Dowód

Wyrażenie na wariancję wynika znatychmiast z podstawienia $n_{h}=p_{h}n$ w ogólnym wzorze (9.7). Nierówność wynika z następującej tożsamości:

$\sigma^{2}=\sum _{{h}}{p_{h}}\sigma _{h}^{2}+\sum _{h}{p_{h}}(\theta _{h}-\theta)^{2},$

(9.12)

gdzie $\theta _{h}=\int f(x)\pi _{h}(x){\rm d}x=\mathbb{E}_{\pi}(f(X)|X\in A_{h})$ . Jest to klasyczny wzór na dekompozycję wariancji na ,,wariancję wewnątrz warstw” (pierwszy składnik w (9.12)) i ,,wariancję pomiędzy warstwami” (drugi składnik w (9.12)). Zdefiniujemy zmienną losową $H$ jako ,,numer warstwy do której wpada $X\sim\pi$ ”, czyli $\{ H=h\}=\{ X\in A_{h}\}$ . Możemy teraz wzór (9.12) przepisać w dobrze znanej postaci

${\rm Var}f(X)=\mathbb{E}{\rm Var}(f(X)|H)+{\rm Var}\mathbb{E}(f(X)|H).$

(9.13)

∎

Wzór (9.12) podpowiada, jak dzielić przestrzeń na warstwy. Największy zysk w porównaniu z losowaniem nie-warstwowym jest wtedy, gdy ,,wariancja międzywarstwowa” jest dużo większa od ,,wewnątrzwarstwowej” Warstwy należy więc wybierać tak, żeby funkcja $\pi(c)f(x)$ była możliwie bliska stałej na każdym zbiorze $A_{h}$ i różniła się jak najbardziej pomiędzy poszczególnymi zbiorami.

Stwierdzenie 9.1 pokazuje, że zawsze zyskujemy na losowaniu warstwowym, jeśli zastosujemy najprostszą, proporcjonalną alokację. Okazuje się, że nie jest to alokacja najlepsza. Jerzy Spława-Neyman odkrył prostą regułę wyznaczania alokacji optymalnej. Wychodzimy od wzoru (9.7) i staramy się zoptymalizować prawą stronę przy warunku $n=\sum _{h}n_{h}$ . Poszukujemy zatem rozwiązania zadania

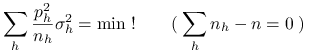$\sum _{{h}}\frac{p_{h}^{2}}{n_{h}}\sigma _{h}^{2}=\min\;!\qquad(\;\sum _{h}n_{h}-n=0\;)$

(9.14)

(względem zmiennych $n_{h}$ ). Zastosujmy metodę mnożników Lagrange'a. Szukamy minimum

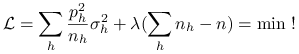${\cal L}=\sum _{{h}}\frac{p_{h}^{2}}{n_{h}}\sigma _{h}^{2}+\lambda(\sum _{h}n_{h}-n)=\min\;!$

(9.15)

Obliczamy pochodną i przyrównujemy do zera:

$\frac{\partial}{\partial n_{h}}{\cal L}=-\frac{p_{h}^{2}}{n_{h}^{2}}\sigma _{h}^{2}+\lambda=0.$

(9.16)

Stąd natychmiast otrzymujemy rozwiązanie: $n_{h}\propto\sigma _{h}p_{h}$ .

Stwierdzenie 9.2 (Alokacja optymalna, J. Neyman)

Estymator warstwowy ma najmniejszą wariancję jeśli alokacja $n$ losowanych punktów jest dana wzorem

$n_{h}=\frac{\sigma _{h}p_{h}}{\sum _{g}\sigma _{g}p_{g}},\qquad(\; h=1,\ldots,k\;).$

(9.17)

Zignorowaliśmy tutaj niewygodne wymaganie, że liczności próbek $n_{h}$ muszą być całkowite. Gdyby to wziąć pod uwagę, rozwiązanie stałoby się skomplikowane, a zysk praktyczny z tego byłby znikomy. W praktyce rozwiązanie neymanowskie zaokrągla się do liczb całkowitych i koniec. Ważniejszy jest inny problem. Żeby wyznaczyć alokację optymalną, trzeba znać nie tylko prawdopodobieństwa $p_{h}$ ale i wariancje warstwowe $\sigma _{h}^{2}$ . W praktyce często opłaca się wylosować wstępne próbki, na podstawie których estymuje się wariancje $\sigma _{h}^{2}$ . Dopiero potem alokuje się dużą, roboczą próbkę rozmiaru $n$ , która jest wykorzystana do obliczania docelowej całki.

9.2. Zmienne kontrolne

Idea zmiennych kontrolnych polega na rozbiciu docelowej całki (wartości oczekiwanej) na dwa składniki, z których jeden umiemy obliczyć analitycznie. Metodę Monte Carlo stosujemy do drugiego składnika. Przedstawmy wielkość obliczaną w postaci

$\theta=\mathbb{E}_{\pi}f(X)=\int _{{{\cal X}}}f(x)\pi(x){\rm d}x=\int _{{{\cal X}}}[f(x)-k(x)]\pi(x){\rm d}x+\int _{{{\cal X}}}k(x)\pi(x){\rm d}x.$

(9.18)

Dążymy do tego, żeby całka funkcji $k$ była obliczona analitycznie (lub numerycznie) a różnica $f-k$ była możliwie bliska stałej, bo wtedy wariancja metody Monte Carlo jest mała. Funkcję $k$ lub zmienną losową $k(X)$ nazywamy zmienną kontrolną.

Dla uproszczenia połóżmy $Y=f(X)$ , gdzie $X\sim\pi$ . Przypuśćmy, że zmiennej kontrolnej będziemy szukać pośród kombinacji liniowych funkcji $k_{1},\ldots,k_{d}$ o znanych całkach. Niech $Z_{j}=k_{j}(X)$ i $Z=(Z_{1},\ldots,Z_{d})^{\top}$ . Przy tym stale pamiętajmy, że $X\sim\pi$ i będziemy pomijać indeks $\pi$ przy wartościach oczekiwanych i wariancjach. Zatem

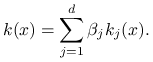$k(x)=\sum _{{j=1}}^{{d}}\beta _{j}k_{j}(x).$

(9.19)

Innymi słowy poszukujemy wektora współczynników $\beta=(\beta _{1},\ldots,\beta _{d})^{\top}$ który minimalizuje wariancję ${\rm Var}(Y-\beta^{\top}Z)$ . Wykorzystamy następujący standardowy wynik z teorii regresji liniowej.

Stwierdzenie 9.3

Niech $Y$ i $Z$ będą zmiennymi losowymi o skończonych drugich momentach, wymiaru odpowiednio $1$ i $d$ . Zakładamy dodatkowo odwracalność macierzy wariancji-kowariancji ${\rm VAR}(Z)$ . Kowariancję pomiędzy $Y$ i $Z$ traktujemy jako wektor wierszowy i oznaczamy przez ${\rm COV}(Y,Z)$ Spośród zmiennych losowych postaci $Y-\beta^{\top}Z$ , najmniejszą wariancję otrzymujemy dla

$\beta _{*}^{\top}={\rm COV}(Y,Z){\rm VAR}(Z)^{{-1}}.$

(9.20)

Ta najmniejsza wartość wariancji jest równa

${\rm Var}(Y-\beta _{*}^{\top}Z)={\rm Var}Y-{\rm COV}(Y,Z){\rm VAR}(Z)^{{-1}}{\rm COV}(Z,Y).$

(9.21)

Przepiszmy tem wynik w bardziej sugestywnej formie. Niech ${\rm Var}Y=\sigma^{2}$ . Można pokazać, że $\beta _{*}$ maksymalizuje korelację pomiędzy $Y$ i $\beta^{\top}Z$ . Napiszmy

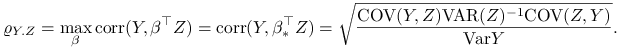$\varrho _{{Y.Z}}=\max _{\beta}{\rm corr}(Y,\beta^{\top}Z)={\rm corr}(Y,\beta _{*}^{\top}Z)=\sqrt{\frac{{\rm COV}(Y,Z){\rm VAR}(Z)^{{-1}}{\rm COV}(Z,Y)}{{\rm Var}Y}}.$

(9.22)

Niech teraz ${\hat{\theta}_{{n}}}^{{\rm contr}}$ będzie estymatorem zmiennych kontrolnych. To znaczy, że losujemy próbkę $X_{1},\ldots,X_{n}\sim\pi$ ,

${\hat{\theta}_{{n}}}^{{\rm contr}}=\frac{1}{n}\sum(Y_{i}-\beta _{*}^{\top}Z_{i})+\beta _{*}^{\top}\mu,$

(9.23)

gdzie $Z_{i}^{\top}=(Z_{{i1}},\ldots,Z_{{in}})=(f_{1}(X_{i}),\ldots,f_{d}(X_{i}))$ , zaś $\mu _{j}=\mathbb{E}f_{j}(X)$ są obliczone analitycznie lub numerycznie $\mu=(\mu _{1},\ldots,\mu _{d})^{\top}$ . Wariancja estymatora jest wyrażona wzorem

${\rm Var}{\hat{\theta}_{{n}}}^{{\rm contr}}=\frac{1}{n}\sigma^{2}(1-\varrho _{{Y.Z}}^{2}),$

(9.24)

co należy porównać z wariancją $\sigma^{2}/n$ ,,zwykłego” estymatora.

Zróbmy podobną uwagę, jak w poprzednim podrozdziale. Optymalny wybór współczynników regresji wymaga znajomości wariancji i kowariancji, których obliczenie może być …(i jest zazwyczaj!) trudniejsze niż wyjściowe zadanie obliczenia wartości oczekiwanej. Niemniej, można najpierw wylosować wstępną próbkę, wyestymować potrzebne wariancje i kowariancje (nawet niezbyt dokładnie) po to, żeby dla dużej, roboczej próbki skonstruować dobre zmienne kontrolne.

Wspomnijmy na koniec, że dobieranie zmiennej kontrolnej metodą regresji liniowej nie jest jedynym sposobem. W konkretnych przykładach można spotkać najróżniejsze, bardzo pomysłowe konstrukcje, realizujące podstawową ideę zmiennych kontrolnych.

9.3. Zmienne antytetyczne

Przypuśćmy, że estymujemy wielkość $\theta=\mathbb{E}_{\pi}f(X)$ . Jeśli mamy dwie zmienne losowe $X$ i $X^{\prime}$ o jednakowym rozkładzie $\pi$ ale nie zakładamy ich niezależności, to

${\rm Var}\frac{f(X)+f(X^{\prime})}{2}=\frac{1}{2}{\rm Var}(X)\left[1+{\rm corr}(f(X),f(X^{\prime}))\right]=\frac{1}{2}\sigma^{2}(1+\varrho).$

Jeśli $\varrho={\rm corr}(f(X),f(X^{\prime}))<0$ , to wariancja w powyższym wzorze jest mniejsza niż $\sigma^{2}/2$ , czyli mniejsza niż w przypadku niezależności $X$ i $X^{\prime}$ . To sugeruje, żeby zamiast losować niezależnie $n$ zmiennych $X_{1},\ldots,X_{n}$ , wygenerować pary zmiennych ujemnie skorelowanych. Załóżmy, że $n=2k$ i mamy $k$ niezależnych par $(X_{1},X_{1}^{\prime}),\ldots,(X_{k},X_{k}^{\prime})$ , a więc łącznie $n$ zmiennych. Porównajmy wariancję ,,zwykłego” estymatora ${\hat{\theta}_{{n}}}^{{\rm CMC}}$ i estymatora ${\hat{\theta}_{{n}}}^{{\rm ant}}$ wykorzystującego ujemne skorelowanie par:

$\begin{split}{\hat{\theta}_{{n}}}^{{\rm CMC}}&=\frac{1}{n}\sum _{{i=1}}^{{n}}f(X_{i}),\qquad{\rm Var}{\hat{\theta}_{{n}}}^{{\rm CMC}}=\frac{\sigma^{2}}{n}\\ {\hat{\theta}_{{n}}}^{{\rm ant}}&=\frac{1}{n}\sum _{{i=1}}^{{n/2}}[f(X_{i})=f(X_{i}^{\prime})],\qquad{\rm Var}{\hat{\theta}_{{n}}}^{{\rm ant}}=\frac{\sigma^{2}}{n}(1+\varrho).\\ \end{split}$

Wariancja estymatora ${\hat{\theta}_{{n}}}^{{\rm ant}}$ jest tym mniejsza, im $\varrho$ bliższe $-1$ (im bardziej ujemnie skorelowane są pary). Standardowym sposobem generowania ujemnie skorelowanych par jest odwracanie dystrybuanty z użyciem ,,odwróconych loczb losowych”.

Stwierdzenie 9.4

Jeśli $h:]0,1[\to\mathbb{R}$ jest funkcją monotoniczną różną od stałej, $\int _{0}^{1}h(u)^{2}{\rm d}u<\infty$ i $U\sim{\rm U}(0,1)$ , to

${\rm Cov}(h(U),h(1-U))<0.$

(9.25)

Dowód

Bez straty ogólności załóżmy, że $h$ jest niemalejąca. Niech $\mu=\mathbb{E}h(U)=\int _{0}^{1}h(u){\rm d}u$ i $t=\sup\{ u:h(1-u)>\mu\}$ . Łatwo zauważyć, że $0<t<1$ . Zauważmy, że

$\begin{split}{\rm Cov}(h(U),h(1-U))&=\mathbb{E}h(U)[h(1-U)-\mu]\\ &=\int _{0}^{1}h(u)[h(1-u)-\mu]{\rm d}u\\ &=\int _{0}^{t}h(u)[h(1-u)-\mu]{\rm d}u+\int _{t}^{1}h(u)[h(1-u)-\mu]{\rm d}u\\ &<\int _{0}^{t}h(t)[h(1-u)-\mu]{\rm d}u+\int _{t}^{1}h(t)[h(1-u)-\mu]{\rm d}u\\ &=h(t)\int _{0}^{1}[h(1-u)-\mu]{\rm d}u=0,\end{split}$

(9.26)

ponieważ dla $0<u<t$ mamy $h(1-u)-\mu>0$ i dla $t<u<1$ mamy $h(1-u)-\mu\geq 0$ .

∎

Przypomnijmy, że dla dowolnej dystrybuanty $G$ określamy uogólnioną funkcję odwrotną $G^{-}$ następującym wzorem:

$G^{-}(u)=\inf\{ x:G(x)\geq u\}.$

(9.27)

Natychmiast wnioskujemy ze Stwierdzenia 9.4, że ${\rm Cov}(G^{-}(U),G^{-}(1-U))<0$ . W ten sposób możemy produkować ujemnie skorelowane pary zmiennych o zadanej dystrybuancie. Okazuje się, że są to najbardziej ujemnie skorelowane pary. Jeśli $X\sim G$ i $X^{\prime}\sim G$ , to

${\rm Cov}(X,X^{\prime})\geq{\rm Cov}(G^{-}(U),G^{-}(1-U)).$

(9.28)

Powyższy fakt ma oczywiste znaczenie z punktu widzenia metod Monte Carlo. Udowodnimy ogólniejsze twierdzenie.

Twierdzenie 9.1

Jeżeli $X\sim F$ , $Y\sim G$ oraz $\mathbb{E}X^{2}<\infty$ , $\mathbb{E}Y^{2}<\infty$ to

${\rm Cov}(F^{-}(U),G^{-}(1-U))\leq{\rm Cov}(X,Y)\leq{\rm Cov}(F^{-}(U),G^{-}(U)).$

(9.29)

Twierdzenie 9.2 wynika z trzech poniższych faktów. Każdy z nich jest sam w sobie interesujący. Zaczniemy od sławnego wyniku Frecheta.

Twierdzenie 9.2 (Ograniczenia Frecheta)

Jeżeli $\mathbb{P}(X\leq x)=F(x)$ , $\mathbb{P}(Y\leq x)=G(y)$ oraz $\mathbb{P}(X\leq x,Y\leq y)=H(x,y)$ oznaczają, odpowiednio, dystrybuanty brzegowe oraz łączną dystrybuantę dwóch zmiennych losowych to

$\max(0,F(x)+G(y)-1)\leq H(x,y)\leq\min(F(x),G(y)).$

(9.30)

Istnieją rozkłady łączne o brzegowych $F$ i $G$ , dla których jest osiągane ograniczenie dolne i ograniczenie górne.

Dowód

Ograniczenie górne wynika z oczywistych nierówności

$\begin{split}\mathbb{P}(X\leq x,Y\leq y)&\leq\mathbb{P}(X\leq x)=F(x),\\ \mathbb{P}(X\leq x,Y\leq y)&\leq\mathbb{P}(Y\leq y)=G(y).\\ \end{split}$

(9.31)

Ograniczenie dolne jest równie proste:

$\begin{split}\mathbb{P}(X\leq x,Y\leq y)&=\mathbb{P}(X\leq x)-\mathbb{P}(X\leq x,Y>y)\\ &\geq\mathbb{P}(X\leq x)-\mathbb{P}(Y>y)=F(x)-[1-G(y)].\end{split}$

(9.32)

∎

Pozostała do pokazania osiągalność. Następujący lemat jest jednym z piękniejszych przykładów ,,symulacyjnego punktu widzenia” w rachunku prawdopodobieństwa.

Lemat 9.1

Jeśli $U\sim{\rm U}(0,1)$ to

$\begin{split}\mathbb{P}(F^{-}(U)\leq x,G^{-}(U)\leq y)&=\min(F(x),G(y));\\ \mathbb{P}(F^{-}(U)\leq x,G^{-}(1-U)\leq y)&=\max(0,F(x)+G(y)-1).\end{split}$

(9.33)

Dowód

Pierwsza równość jest oczywista:

$\begin{split}\mathbb{P}(F^{-}(U)\leq x,G^{-}(U)\leq y)&=\mathbb{P}(U\leq F(x),U\leq G(y))\\ &=\min(F(x),G(y)).\end{split}$

(9.34)

Druga równość też jest oczywista:

$\begin{split}\mathbb{P}(F^{-}(U)\leq x,G^{-}(1-U)\leq y)&=\mathbb{P}(U\leq F(x),1-U\leq G(y))\\ &=\mathbb{P}(1-G(y)\leq U\leq F(x))\\ &=\max(0,F(x)-[1-G(y)]).\end{split}$

(9.35)

∎

Głębokie twierdzenie Frecheta składa się więc z kilku dość oczywistych spostrzeżeń. Zeby udowodnić Twierdzenie 9.1 potrzeba jeszcze jednego ciekawego lematu.

Lemat 9.2

Niech $F(x)$ , $G(y)$ i $H(x,y)$ oznaczają, odpowiednio, dystrybuanty brzegowe oraz łączną dystrybuantę zmiennych losowych $X$ i $Y$ . Jeśli $\mathbb{E}X^{2}<\infty$ , $\mathbb{E}Y^{2}<\infty$ to

${\rm Cov}(X,Y)=\iint[H(x,y)-F(x)F(y)]{\rm d}x{\rm d}y.$

(9.36)

Dowód

Niech $(X_{1},Y_{1})$ i $(X_{2},Y_{2})$ będą niezależnymi parami o jednakowym rozkładzie takim jak para $(X,Y)$ . Wtedy

$\begin{split} 2{\rm Cov}(X,Y)&=\mathbb{E}(X_{1}-X_{2})(Y_{1}-Y_{2})\\ &=\mathbb{E}\iint[\mathbb{I}(X_{1}\leq x)-\mathbb{I}(X_{2}\leq x)][\mathbb{I}(Y_{1}\leq y)-\mathbb{I}(Y_{2}\leq y)]{\rm d}x{\rm d}y\\ &=\iint\mathbb{E}[\mathbb{I}(X_{1}\leq x)-\mathbb{I}(X_{2}\leq x)][\mathbb{I}(Y_{1}\leq y)-\mathbb{I}(Y_{2}\leq y)]{\rm d}x{\rm d}y\\ &=\iint[\mathbb{P}(X_{1}\leq x,Y_{1}\leq y)+\mathbb{P}(X_{2}\leq x,Y_{2}\leq y)\\ &\qquad\qquad\qquad-\mathbb{P}(X_{1}\leq x,Y_{2}\leq y)-\mathbb{P}(X_{2}\leq x,Y_{1}\leq y)]{\rm d}x{\rm d}y\\ &=\iint[2\mathbb{P}(X\leq x,Y\leq y)-2\mathbb{P}(X\leq x)\mathbb{P}(Y\leq y)]{\rm d}x{\rm d}y.\\ \end{split}$

(9.37)

∎

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Symulacje stochastyczne i metody Monte Carlo

Zagadnienia

9. Algorytmy Monte Carlo II. Redukcja wariancji

9.1. Losowanie warstwowe

Stwierdzenie 9.1 (Alokacja proporcjonalna)

Dowód

Stwierdzenie 9.2 (Alokacja optymalna, J. Neyman)

9.2. Zmienne kontrolne

Stwierdzenie 9.3

9.3. Zmienne antytetyczne

Stwierdzenie 9.4

Dowód

Twierdzenie 9.1

Twierdzenie 9.2 (Ograniczenia Frecheta)

Dowód

Lemat 9.1

Dowód

Lemat 9.2

Dowód