Zagadnienia

10.1 Co to jest MCMC ?
10.2 Łańcuchy Markowa
- 10.2.1 Rozkład stacjonarny
- 10.2.2 Twierdzenia graniczne dla łańcuchów Markowa

10. Markowowskie Monte Carlo I. Wprowadzenie

10.1. Co to jest MCMC ?

W pewnych sytuacjach okazuje się, że wygenerowanie zmiennej losowej $X$ z interesującego nas rozkładu prawdopodobieństwa $\pi$ jest praktycznie niemożliwe. Wyobraźmy sobie, że $\pi$ jest bardzo skomplikowanym rozkładem na ,,ogromnej”, wielowymiarowej przestrzeni ${\cal X}$ . Zazwyczaj ten rozkład jest dany poprzez podanie funkcji proporcjonalnej do gęstości, $p^{{\prime}}\propto p$ , ale bez znajomości stałej normującej $1/\int p^{{\prime}}$ . Przy tym ,,ogromna” przestrzeń ${\cal X}$ może być zbiorem skończonym (ale bardzo licznym) zaś rozkład $\pi$ może być… jednostajny, o gęstości $p\propto 1$ . Jeśli jednak nośnik rozkładu ${\rm U}({\cal X})$ jest bardzo ,,skomplikowanym” zbiorem, to metody typu eliminacji/akceptacji mogą zawieść. Właśnie z takim przypadkiem spotkaliśmy się już we wstępnym Rozdziale 1, w Przykładzie 1.5. Naszkicowany tam algorytm jest przedstawicielem metod, którymi obecnie zajmiemy się dokładniej, czyli algorytmów MCMC. Ten skrót oznacza Markov Chain Monte Carlo, czyli po polsku algorytmy MC wykorzystujące łańcuchy Markowa. Podstawowa idea jest taka: jeśli nie umiemy generować zmiennej losowej $X$ o rozkładzie $\pi$ to zadowolimy się generowaniem ciągu zmiennych losowych $X_{0},X_{1},\ldots,X_{n},\ldots$ , który w pewnym sensie zbliża się, zmierza do rozkładu $\pi$ . Podobnie jak w cytowanym przykładzie ,,plecakowym” ciąg $X_{n}$ ma charakter ,,losowego błądzenia” po przestrzeni ${\cal X}$ .

To wszystko co dotychczas powiedzieliśmy jest bardzo niekonkretne i wymaga uściślenia. W moich wykładach ścisłe przedstawienie tych zagadnień będzie możliwe tylko w ograniczonym zakresie. W obecnym rozdziale skupię się na głównych ideach MCMC. Następnie, w Rozdziałach 11 i 12 przedstawię podstawowe algorytmy i kilka motywujących przykładów, pokażę wyniki symulacji, ale niemal nic nie udowodnię. Sprobuję to częściowo naprawić w Rozdziałach 14 i 15 , które w całości będą poświęcone łańcuchom Markowa i algorytmom MCMC na skończonej przestrzeni ${\cal X}$ . W tej uproszczonej sytuacji podam dowody (a przynajmniej szkice dowodów) podstawowych twierdzeń. Zastosowania MCMC w przypadku ,,ciągłej” przestrzeni ${\cal X}$ (powiedzmy, ${\cal X}\subseteq\mathbb{R}^{d}$ ) są przynajmniej równie ważne i w gruncie rzeczy bardzo podobne. Zobaczymy to na paru przykładach. Algorytmy MCMC pracujące na przestrzeni ciągłej są w zasadzie takie same jak te w przypadku przestrzeni skończonej, ale ich analiza robi się trudniejsza, wymaga więcej abstrakcyjnej matematyki – i w rezultacie wykracza poza zakres mojego skryptu. Ograniczę się w tej materii do kilku skromnych uwag. Bardziej systematyczne, a przy tym dość przystępne przedstawienie ogólnej teorii można znaleźć w [20] lub [17].

10.2. Łańcuchy Markowa

Klasyczne metody MCMC, jak sama nazwa wskazuje, opierają się na generowaniu łańcucha Markowa. Co prawda, rozwijają się obecnie bardziej wyrafinowane metody MCMC (zwane adaptacyjnymi), które wykorzystują procesy niejednorodne a nawet nie-markowowskie. Na razie ograniczymy się do rozpatrzenia sytuacji, gdy generowany ciąg zmiennych losowych $X_{n}$ jest jednorodnym łańcuchem Markowa na przestrzeni ${\cal X}$ . Jeśli ${\cal X}$ jest zbiorem skończonym, możemy posługiwać się Definicją 7.1, w ogólnym przypadku – Definicją 7.2. Przypomnijmy oznaczenie prawdopodobieństw przejścia łańcucha: dla $x\in{\cal X}$ oraz $B\subseteq{\cal X}$ ,

$\mathbb{P}(X_{{n+1}}\in B|X_{n}=x)=P(x,B).$

W przypadku przestrzeni skończonej wygodniej posługiwać się macierzą przejścia o elementach

$\mathbb{P}(X_{{n+1}}=y|X_{n}=x)=P(x,y).$

Metoda generowania łańcuchów Markowa jest dość oczywista i sprowadza się do wzorów (7.2) w przypadku skończonym i (7.5) w przypadku ogólnym.

10.2.1. Rozkład stacjonarny

Niech $\pi$ oznacza docelowy rozkład prawdopodobieństwa. Chcemy tak generować łańcuch $X_{n}$ , czyli tak wybrać prawdopodobieństwa przejścia $P$ , aby uzyskać zbieżność do rozkładu $\pi$ . Spróbujemy uściślić co to znaczy, w jakim sensie rozumiemy zbieżność.

Definicja 10.1

Mówimy, że $\pi$ jest rozkładem stacjonarnym (lub rozkładem równowagi) łańcucha Markowa o prawdopodobieństwach przejścia $P$ , jeśli dla każdego (mierzalnego) zbioru $B\subseteq{\cal X}$ mamy

$\pi(B)=\int _{{{\cal X}}}\pi({\rm d}x)P(x,B).$

W przypadku skończonej przestrzeni ${\cal X}$ równoważne sformułowanie jest takie: dla każdego stanu $y$ ,

$\pi(y)=\sum _{{x\in{\cal X}}}\pi(x)P(x,y).$

Jeśli rozkład początkowy jest rozkładem stacjonarnym, $\mathbb{P}(X_{0}\in\cdot)=\pi(\cdot)$ , to mamy $\mathbb{P}(X_{n}\in\cdot)=\pi(\cdot)$ dla każdego $n$ . Co więcej, w takiej sytuacji łączny rozkład zmiennych $X_{n},X_{{n+1}},\ldots$ jest taki sam, jak rozkład zmiennych $X_{0},X_{1},\ldots$ . Mówimy, że łańcuch jest w położeniu równowagi lub, ze jest procesem stacjonarnym. To uzasadnia nazwę rozkładu stacjonarnego. Oczywiście, łańcuchy generowane przez algorytmy MCMC nie są w stanie równowagi, bo z założenia nie umiemy wygenerować $X_{0}\sim\pi$ . Generujemy $X_{0}$ z pewnego innego rozkładu $\xi$ , nazywanego rozkładem początkowym. Gdy zajdzie potrzeba, żeby uwidocznić zależność od rozkładu początkowego, będziemy używali oznaczeń $\mathbb{P}_{{\xi}}(\cdots)$ i $\mathbb{E}_{{\xi}}(\cdots)$ . Przeważnie start jest po prostu deterministyczny, czyli $\xi$ jest rozkładem skupionym w pewnym punkcie $x\in{\cal X}$ . Piszemy wtedy $\mathbb{P}_{{x}}(\cdots)$ i $\mathbb{E}_{{x}}(\cdots)$ .

Jeśli $\pi$ jest rozkładem stacjonarnym, to przy pewnych dodatkowych założeniach uzyskuje się tak zwane Słabe Twierdzenie Ergodyczne (STE). Jego tezą jest zbieżność rozkładów prawdopodobieństwa zmiennych losowych $X_{n}$ do $\pi$ w następującym sensie: dla dowolnego (mierzalnego) zbioru $B\subseteq{\cal X}$ i dowolnego rozkładu początkowego $\xi$ mamy

$\qquad\mathbb{P}_{\xi}(X_{n}\in B)\to\pi(B)\qquad(n\to\infty).$

(10.1)

Dla skończonej przestrzeni ${\cal X}$ równoważne jest stwierdzenie, że dla każdego $y\in{\cal X}$ ,

$\mathbb{P}_{\xi}(X_{n}=y)\to\pi(y)\qquad(n\to\infty).$

Pewną wersję STE dla skończonej przestrzeni ${\cal X}$ udowodnimy w następnym rozdziale (Twierdzenie 14.5). Na razie poprzestańmy na następującym prostym spostrzeżeniu.

Uwaga 10.1

Jeżeli zachodzi teza STE dla pewnego rozkładu granicznego $\pi _{\infty}$ , czyli $P^{n}(x,B)\to\pi _{\infty}(B)$ dla dowolnych $x\in{\cal X}$ , $B\subseteq{\cal X}$ , to $\pi _{\infty}$ jest rozkładem stacjonarnym. W istocie, wystarczy przejść do granicy w równości

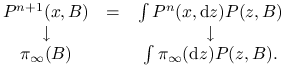$\begin{matrix}P^{{n+1}}(x,B)&=&\int P^{n}(x,{\rm d}z)P(z,B)\\ \downarrow&&\downarrow\\ \pi _{\infty}(B)&&\int\pi _{\infty}({\rm d}z)P(z,B).\end{matrix}$

Co więcej, $\pi _{\infty}$ jest jedynym rozkładem stacjonarnym.

Uwaga 10.2

W teorii łańcuchów Markowa rozważa się różne pojęcia zbieżności rozkładów. Zauważmy, że w powyżej przytoczonej tezie STE oraz w Uwadze 10.1 mamy do czynienia z silniejszym rodzajem zbieżności, niż poznana na rachunku prawdopodobieństwa zbieżność słaba (według rozkładu), oznaczana $\to _{{\rm d}}$ .

10.2.2. Twierdzenia graniczne dla łańcuchów Markowa

Naszkicujemy podstawowe twierdzenia graniczne dla łańcuchów Markowa. Dokładniejsze sformułowania i dowody pojawią się w następnym rozdziale i będą ograniczone do przypadku skończonej przestrzeni ${\cal X}$ . Bardziej dociekliwych Czytelników muszę odesłać do przeglądowych prac [20, 13].

Sformułujemy najpierw odpowiednik Mocnego Prawa Wielkich Liczb (PWL) dla łańcuchów Markowa. Rozważmy funkcję $f:{\cal X}\to\mathbb{R}$ . Wartość oczekiwana funkcji $f$ względem rozkładu $\pi$ jest określona jako całka

$\mathbb{E}_{\pi}f=\int _{{{\cal X}}}f(x)\pi({\rm d}x).$

Jeżeli rozkład $\pi$ ma gęstość $p$ względem miary Lebesgue'a to jest to ,,zwyczajna całka”,

$\mathbb{E}_{\pi}f=\int _{{{\cal X}}}f(x)p(x){\rm d}x.$

W przypadku dyskretnej przestrzeni ${\cal X}$ jest to suma

$\mathbb{E}_{\pi}f=\sum _{{x\in{\cal X}}}f(x)\pi(x).$

Jeśli załóżmy $\pi$ jest rozkładem stacjonarnym łańcucha Markowa $X_{n}$ , to możemy oczekiwać, że zachodzi zbieżność średnich do granicznej wartości oczekiwanej,

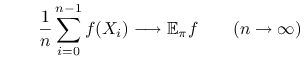$\qquad{1\over n}\sum _{{i=0}}^{{n-1}}f(X_{i})\longrightarrow\mathbb{E}_{\pi}f\qquad(n\to\infty)$

(10.2)

z prawdopodobieństwem 1. W istocie, można udowodnić (10.2) przy pewnych dodatkowych założeniach. Mówimy wtedy, że zachodzi PWL lub Mocne Twierdzenie Ergodyczne. Ze względu na zastosowania MCMC, wymagamy aby (10.2) zachodziło dla dowolnego rozkładu początkowego $\xi$ (a nie dla $\xi=\pi$ , czyli dla łańcucha stacjonarnego). Jedną z wersji PWL dla łańcuchów Markowa przedstawimy, wraz z pięknym i prostym dowodem, w Rozdziale 14 rozdziale (Twierdzenie 14.3).

Centralne Twierdzenie Graniczne (CTG) dla łańcuchów Markowa ma tezę następującej postaci. Dla dowolnego rozkładu początkowego $\xi$ zachodzi zbieżność według rozkładu:

$\qquad\frac{1}{\sqrt{n}}\left(\sum _{{i=0}}^{{n-1}}[f(X_{i})-\mathbb{E}_{\pi}f]\right)\longrightarrow{\rm N}\big(0,{\sigma _{{\rm as}}^{{2}}(f)}\big)\quad(n\to\infty).$

(10.3)

Liczba ${\sigma _{{\rm as}}^{{2}}(f)}$ , zwana asymptotyczną wariancją, nie zależy od rozkładu początkowego ${\xi}$ , zależy zaś od macierzy przejścia $P$ i funkcji $f$ . Ponadto można udowodnić następujący fakt: dla dowolnego rozkładu początkowego $\xi$ ,

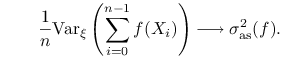$\qquad\frac{1}{n}{\rm Var}_{\xi}\left(\sum _{{i=0}}^{{n-1}}f(X_{i})\right)\longrightarrow{\sigma _{{\rm as}}^{{2}}(f)}.$

(10.4)

Przy pewnych dodatkowych założeniach, asymptotyczną wariancję można wyrazić w terminach ,,stacjonarnych kowariancji” jak następuje. Mamy

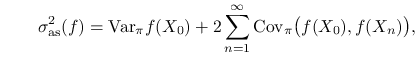$\qquad{\sigma _{{\rm as}}^{{2}}(f)}={\rm Var}_{\pi}f(X_{0})+2\sum _{{n=1}}^{\infty}{\rm Cov}_{\pi}\big(f(X_{0}),f(X_{n})\big),$

(10.5)

gdzie ${\rm Var}_{\pi}$ i ${\rm Cov}_{\pi}$ oznaczają, oczywiście, wariancję i kowariancję obliczoną przy założeniu, że łańcuch jest stacjonarny. Niech

$\begin{split}\sigma^{2}(f)=&{\rm Var}_{\pi}f(X_{0});\\ \sigma^{2}(f)\rho _{n}(f)=&{\rm Cov}_{\pi}\big[f(X_{0}),f(X_{n})\big],\end{split}$

Przyjmijmy jeszcze, że $\rho _{n}(f)=\rho _{{-n}}(f)$ . To określenie jest naturalne bo łańcuch stacjonarny można ,,przedłużyć wstecz”. Wzór (10.5) można przepisać tak:

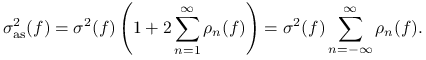${\sigma _{{\rm as}}^{{2}}(f)}=\sigma^{2}(f)\left(1+2\sum _{{n=1}}^{\infty}\rho _{n}(f)\right)=\sigma^{2}(f)\sum _{{n=-\infty}}^{\infty}\rho _{n}(f).$

Później pojawi się kilka innych wzorów na asymptotyczną wariancję.

W tym miejscu chcę podkreślić różnicę między stacjonarną wariancją $\sigma^{2}(f)={\rm Var}_{\pi}f={\rm Var}_{\pi}f(X_{n})$ i asymptotyczną wariancją ${\sigma _{{\rm as}}^{{2}}(f)}$ . W większości zastosowań kowariancje we wzorze (10.5) są dodatnie (zmienne losowe $f(X_{0})$ i $f(X_{k})$ są dodatnio skorelowane). W rezultacie ${\sigma _{{\rm as}}^{{2}}(f)}$ jest dużo większa od $\sigma^{2}(f)$ . To jest cena, którą płacimy za używanie łańcucha Markowa zamiast ciągu zmiennych niezależnych, jak w Rozdziale 8.

Zauważmy, że algorytmy Monte Carlo przeważnie mają za zadanie obliczyć pewną wartość oczekiwaną, a więc wielkość postaci $\theta=\mathbb{E}_{\pi}f$ . Jeśli potrafimy generować łańcuch Markowa zbieżny do $\pi$ , to naturalnym estymatorem $\mathbb{E}_{\pi}f$ jest

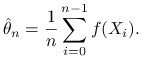${\hat{\theta}_{{n}}}={1\over n}\sum _{{i=0}}^{{n-1}}f(X_{i}).$

Możemy tezy PWL oraz CTG zapisać w skrócie tak:

$\begin{split}{\hat{\theta}_{{n}}}&\longrightarrow _{{\rm p.n.}}\theta\qquad(n\to\infty),\\ \sqrt{n}\left({\hat{\theta}_{{n}}}-\theta\right)&\longrightarrow _{{\rm d}}{\rm N}\big(0,{\sigma _{{\rm as}}^{{2}}(f)}\big),\quad(n\to\infty).\end{split}$

PWL gwarantuje zgodność estymatora, a więc w pewnym sensie poprawność metody. Jest to, rzecz jasna, zaledwie wstęp do dokładniejszej analizy algorytmu. Zauważmy, że CTG może służyć do budowania asymptotycznych przedziałów ufności dla estymowanej wielkości $\theta$ : jeśli przyjmiemy poziom ufności $1-\alpha$ i dobierzemy odpowiedni kwantyl $z$ rozkładu normalnego, to

${\lim _{{n\to\infty}}}\mathbb{P}\left(|{\hat{\theta}_{{n}}}-\theta|\leqslant\frac{z{\sigma _{{\rm as}}(f)}}{\sqrt{n}}\right)=\Phi(z)-\Phi(-z)=1-\alpha.$

Oczywiście, $\Phi(z)$ oznacza to dystrybuantę rozkładu ${\rm N}(0,1)$ i $\Phi(z)=1-\alpha/2$ . Potrzebne jest jeszcze oszacowanie asymptotycznej wariancji ${\sigma _{{\rm as}}^{{2}}(f)}$ , co nie jest wcale łatwe. Co więcej, CTG nie daje żadnej informacji o tym, dla jakich $n$ przybliżenie rozkładem normalnym jest rozsądne.

Graniczne zachowanie wariancji estymatora ${\hat{\theta}_{{n}}}$ wyjaśnia wzór (10.4). Uzupełnijmy to (pomijając chwilowo uzasadnienie) opisem granicznego zachowania obciążenia: przy $n\to\infty$ ,

$\begin{split}\qquad{\rm Var}_{\xi}({\hat{\theta}_{{n}}})&=\frac{1}{n}{\sigma _{{\rm as}}^{{2}}(f)}+o\left(\frac{1}{n}\right),\\ \mathbb{E}_{\xi}{\hat{\theta}_{{n}}}-\theta&=O\left(\frac{1}{n}\right).\end{split}$

Oczywiście, naturalną miarą jakości estymatora jest błąd średniokwadratowy (BŚK). Ponieważ BŚK jest sumą wariancji i kwadratu obciążenia to, przynajmniej w granicy dla $n\to\infty$ , wariancja ma dominujący wpływ, zaś obciążenie staje się zaniedbywalne:

$\qquad\mathbb{E}_{\xi}\left({\hat{\theta}_{{n}}}-\theta\right)^{2}=\frac{1}{n}{\sigma _{{\rm as}}^{{2}}(f)}+o\left(\frac{1}{n}\right).$

(10.6)

Powtóżmy jednak zastrzeżenie dotyczące wszystkich wyników zawartych w tym podrozdziale, Wzór (10.6) tylko sugeruje pewne przybliżenie interesującej nas wielkości.

Sławne i ważne twierdzenia graniczne sformułowane w tym podrozdziale nie są, niestety, całkowicie zadowalającym narzędziem analizy algorytmów Monte Carlo. Algorytmy wykorzystujące łańcuchy Markowa są użyteczne wtedy, gdy osiągają wystarczającą dokładność dla liczby kroków $n$ znikomo małej w porównaniu z rozmiarem przestrzeni stanów. W przeciwnym przypadku można po prostu deterministycznie ,,przejrzeć wszystkie stany” i dokładnie obliczyć interesującą nas wielkość.

Niemniej, twierdzenia graniczne są interesujące z jakościowego punktu widzenia. Ponadto, ważne dla nas oszacowania dotyczące zachowania łańcucha w skończonym czasie można porównać z wielkościami granicznymi, aby ocenić ich jakość.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Symulacje stochastyczne i metody Monte Carlo