11. Markowowskie Monte Carlo II. Podstawowe algorytmy
11.1. Odwracalność
Najważniejsze algorytmy MCMC są oparte na idei odwracalności łańcucha Markowa.
Definicja 11.1
Łańcuch o jądrze ![]() jest odwracalny względem rozkładu prawdopodobieństwa
jest odwracalny względem rozkładu prawdopodobieństwa ![]() , jeśli
dla dowolnych
, jeśli
dla dowolnych ![]() mamy
mamy
W skrócie,
Odwracalność implikuje, że rozkład ![]() jest stacjonarny. jest to dlatego ważne, że sprawdzanie odwracalności
jest stosunkowo łatwe.
jest stacjonarny. jest to dlatego ważne, że sprawdzanie odwracalności
jest stosunkowo łatwe.
Twierdzenie 11.1
Jeśli ![]() to
to ![]() .
.
Dowód
![]() .
.
11.2. Algorytm Metropolisa-Hastingsa
To jest pierwszy historycznie i wciąż najważniejszy algorytm MCMC. Zakładamy, że umiemy generować łańcuch Markowa z pewnym jądrem
![]() . Pomysł Metropolisa polega na tym, żeby zmodyfikować ten łańcuch wprowadzając specjalnie dobraną regułę akceptacji w
taki sposób, żeby wymusić zbieżność do zadanego rozkładu
. Pomysł Metropolisa polega na tym, żeby zmodyfikować ten łańcuch wprowadzając specjalnie dobraną regułę akceptacji w
taki sposób, żeby wymusić zbieżność do zadanego rozkładu ![]() . W dalszym ciągu systematycznie utożsamiamy rozkłady prawdopodobieństwa z
ich gęstościami, aby nie mnożyć oznaczeń. Mamy zatem:
. W dalszym ciągu systematycznie utożsamiamy rozkłady prawdopodobieństwa z
ich gęstościami, aby nie mnożyć oznaczeń. Mamy zatem:
-
Rozkład docelowy:
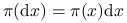 .
. -
Rozkład ,,propozycji”:
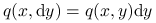 .
. -
Reguła akceptacji:
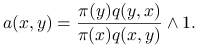
Algorytm Metropolisa-Hastingsa (MH) interpretujemy jako ,,błądzenie losowe” zgodnie z jądrem przejścia ![]() , zmodyfikowane
poprzez odrzucanie niektórych ruchów, przy czym reguła akceptacji/odrzucania zależy w specjalny sposób od
, zmodyfikowane
poprzez odrzucanie niektórych ruchów, przy czym reguła akceptacji/odrzucania zależy w specjalny sposób od
![]() . Pojedynczy krok algorytmu jest następujący.
. Pojedynczy krok algorytmu jest następujący.
| function |
| Gen |
| Gen |
| if |
| begin |
| |
| end |
| |
Łańcuch Markowa powstaje zgodnie z następującym schematem:
| Gen |
| for |
| begin |
| |
| end |
Jądro przejścia M-H jest następujące:
Dla przestrzeni skończonej, jądro łańcucha MH redukuje się do macierzy prawdopodobieństwprzejścia. Wzór jest w tym przypadku
bardzo prosty: dla ![]() ,
,
Twierdzenie 11.2
Jądro przejścia MH jest odwracalne względem ![]() .
.
Dowód
Ograniczmy się do przestrzeni skończonej, żeby nie komplikować oznaczeń. W ogólnym przypadku dowód jest w zasadzie taki sam, tylko napisy stają się mniej czytelne. Niech (bez straty ogólności)
Wtedy
Uwagi historyczne:
-
Metropolis w 1953 zaproponował algorytm, w którym zakłada się symetrię rozkładu propozycji,
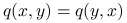 .
Warto zauważyć, że wtedy łańcuch odpowiadający
.
Warto zauważyć, że wtedy łańcuch odpowiadający 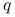 (błądzenie bez eliminacji ruchów) ma rozkład stacjonarny
jednostajny. Reguła akceptacji przybiera postać
(błądzenie bez eliminacji ruchów) ma rozkład stacjonarny
jednostajny. Reguła akceptacji przybiera postać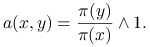
-
Hastings w 1970 uogólnił rozważania na przypadek niesymetrycznego
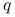 .
.
Uwaga ważna:
-
Algorytm MH wymaga znajomości gęstość
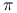 tylko z dokładnością do
proporcjonalności, bez stałej normującej.
tylko z dokładnością do
proporcjonalności, bez stałej normującej.
11.3. Próbnik Gibbsa
Drugim podstawowym algorytmem MCMC jest próbnik Gibbsa (PG) (Gibbs Sampler, GS).
Załóżmy, że przestrzeń na której żyje docelowy rozkład ![]() ma strukturę produktową:
ma strukturę produktową: ![]() .
Przyjmijmy następujące oznaczenia:
.
Przyjmijmy następujące oznaczenia:
-
Jeśli
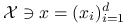 to
to 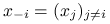 : wektor
z pominiętą
: wektor
z pominiętą 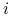 -tą współrzędną.
-tą współrzędną.
-
Rozkład docelowy (gęstość):
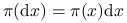 .
. -
Pełne rozkłady warunkowe (full conditionals):
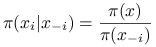
Mały krok PG jest zmianą ![]() -tej współrzędnej (wylosowaniem nowej wartości z rozkładu warunkowego):
-tej współrzędnej (wylosowaniem nowej wartości z rozkładu warunkowego):
Prawdopodobieństwo przejścia małego kroku PG (w przypadku przestrzeni skończonej) jest takie:
Twierdzenie 11.3
Mały krok PG jest ![]() -odwracalny.
-odwracalny.
Dowód
Niech ![]() . Wtedy
. Wtedy
(skorzystaliśmy z symetrii).
∎Oczywiście, trzeba jeszcze zadbać o to, żeby łańcuch generowany przez PG był nieprzywiedlny. Trzeba zmieniać wszystkie współrzędne, nie tylko jedną. Istnieją dwie zasadnicze odmiany próbnika Gibbsa, różniące się spoobem wyboru współrzędnych do zmiany.
-
Losowy wybór współrzędnych, ,,LosPG”.
-
Systematyczny wybór współrzędnych, ,,SystemPG”.
Losowy PG. Wybieramy współrzędną ![]() -tą z prawdopodobieństwem
-tą z prawdopodobieństwem ![]() . .
. .
| function |
| Gen |
| Gen |
| |
| |
Jądro przejścia w ,,dużym” kroku losowego PG jest takie:
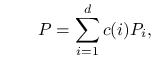 |
LosPG jest odwracalny.
Systematyczny PG. Współrzędne są zmieniane w porządku cyklicznym.
| function |
| begin |
| Gen |
| Gen |
| |
| Gen |
| |
| end |
Jądro przejścia w ,,dużym” kroku systematycznego PGjest następujące.
Systematyczny PG nie jest odwracalny. Ale jest ![]() -stacjonarny, bo
-stacjonarny, bo
![]() .
.
Przy projektowaniu konkretnych realizacji PG pojawia się szereg problemów, ważnych zarówno z praktycznego jak i
teoretycznego punktu widzenia. Jak wybrać rozkład ![]() w losowym PG? Jest raczej jasne, że niektóre współrzędne
powinny być zmieniane częściej, a inne rzadziej. Jak dobrać kolejność współrzędnych w systematycznym PG? Czy ta
kolejność ma wpływ na tempo zbieżności łańcucha. Wreszczie, w wielu przykładach można
zmieniać całe ,,bloki” współrzędnych na raz.
w losowym PG? Jest raczej jasne, że niektóre współrzędne
powinny być zmieniane częściej, a inne rzadziej. Jak dobrać kolejność współrzędnych w systematycznym PG? Czy ta
kolejność ma wpływ na tempo zbieżności łańcucha. Wreszczie, w wielu przykładach można
zmieniać całe ,,bloki” współrzędnych na raz.
Systematyczny PG jest uważany za bardziej efektywny i częściej stosowany w praktyce. Z drugiej strony jest trudniejszy do analizy teoretycznej, niż losowy PG.