13. Markowowskie Monte Carlo IV. Pola losowe
13.1. Definicje
Niech ![]() będzie nieskierowanym grafem. Wyobraźmy sobie, że elementy
będzie nieskierowanym grafem. Wyobraźmy sobie, że elementy ![]() reprezentują ,,miejsca”
w przestrzeni lub na płaszczyźnie, zaś krawędzie grafu łączą miejsca ,,sąsiadujące” ze sobą. Taka
interpretacja jest związana z zastosowaniami do statystyki ,,przestrzennej” i przetwarzania obrazów.
Model, który przedstawimy ma również zupełnie inne interpretacje, ale pozostaniemy przy sugestywnej terminologii
,,przestrzennej”:
reprezentują ,,miejsca”
w przestrzeni lub na płaszczyźnie, zaś krawędzie grafu łączą miejsca ,,sąsiadujące” ze sobą. Taka
interpretacja jest związana z zastosowaniami do statystyki ,,przestrzennej” i przetwarzania obrazów.
Model, który przedstawimy ma również zupełnie inne interpretacje, ale pozostaniemy przy sugestywnej terminologii
,,przestrzennej”:
-
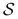 — zbiór miejsc,
— zbiór miejsc, -
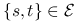 — miejsca
— miejsca 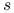 i
i 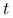 sąsiadują — będziemy wtedy pisać
sąsiadują — będziemy wtedy pisać 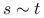 ,
, -
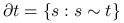 — zbiór sąsiadów miejsca
— zbiór sąsiadów miejsca 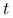 .
.
Niech ![]() będzie skończonym zbiorem. Powiedzmy, że elementy
będzie skończonym zbiorem. Powiedzmy, że elementy ![]() są ,,kolorami”
które mogą być przypisane elementom zbioru
są ,,kolorami”
które mogą być przypisane elementom zbioru ![]() . Konfiguracją nazywamy dowolną funkcję
. Konfiguracją nazywamy dowolną funkcję ![]() .
Będziemy mówić że
.
Będziemy mówić że ![]() jest
jest ![]() -tą współrzędną konfiguracji
-tą współrzędną konfiguracji ![]() i stosować oznaczenia podobne jak dla wektorów:
i stosować oznaczenia podobne jak dla wektorów:
| (13.1) |
W zadaniach przetwarzania obrazów, miejsca są pikslami na ekranie i konfigurację utożsamiamy z ich pokolorowaniem,
a więc z cyfrową reprezentacją obrazu. Zbiór ![]() gra rolę ,,palety kolorów”. Niekiedy założenie o skończoności
zbioru
gra rolę ,,palety kolorów”. Niekiedy założenie o skończoności
zbioru ![]() staje się niewygodne. Dla czarno-szaro-białych obrazów ,,pomalowanych” różnymi odcieniami szarości,
wygodnie przyjąć, że
staje się niewygodne. Dla czarno-szaro-białych obrazów ,,pomalowanych” różnymi odcieniami szarości,
wygodnie przyjąć, że ![]() lub
lub ![]() . Tego typu modyfikacje są dość oczywiste i
nie będę się nad tym zatrzymywał. Dla ustalenia uwagi, wzory w tym podrozdziale dotyczą przypadku skończonego zbioru
,,kolorów”. Przestrzenią konfiguracji jest zbiór
. Tego typu modyfikacje są dość oczywiste i
nie będę się nad tym zatrzymywał. Dla ustalenia uwagi, wzory w tym podrozdziale dotyczą przypadku skończonego zbioru
,,kolorów”. Przestrzenią konfiguracji jest zbiór ![]() . Dla konfiguracji
. Dla konfiguracji ![]() i miejsca
i miejsca ![]() , niech
, niech
-
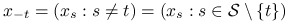 — konfiguracja z pominiętą
— konfiguracja z pominiętą 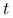 -tą współrzędną,
-tą współrzędną, -
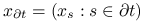 — konfiguracja ograniczona do sąsiadów miejsca
— konfiguracja ograniczona do sąsiadów miejsca 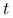 .
.
Jeśli ![]() i
i ![]() to rozkładem Gibbsa nazywamy rozkład prawdopodobieństwa na przestrzeni konfiguracji dany
wzorem
to rozkładem Gibbsa nazywamy rozkład prawdopodobieństwa na przestrzeni konfiguracji dany
wzorem
Ze względu na inspiracje pochodzące z fizyki statystycznej, funkcję ![]() nazywamy energią,
nazywamy energią, ![]() jest (z dokładnością do stałej)
odwrotnością temperatury. Stała normująca wyraża się wzorem
jest (z dokładnością do stałej)
odwrotnością temperatury. Stała normująca wyraża się wzorem
| (13.2) |
i jest typowo niemożliwa do obliczenia.
Oczywiście, każdy rozkład prawdopodobieństwa ![]() na
na ![]() dale się zapisać jako rozkład Gibbsa, jeśli położyć
dale się zapisać jako rozkład Gibbsa, jeśli położyć ![]() ,
, ![]() i
umownie przyjąć, że
i
umownie przyjąć, że ![]() (czyli konfiguracje niemożliwe mają nieskończoną energię). Nie o to jednak chodzi. Ciekawe są rozkłady
Gibbsa, dla których fukcja energii ma specjalną postać związaną z topologią grafu ,,sąsiedztw”. Ograniczymy się do ważnej podklasy
markowowskich pól losowych (MPL), mianowicie do sytuacji gdy energia jest sumą ,,oddziaływań” lub ,,interakcji” między parami
miejsc sąsiadujących i składników zależnych od pojedynczych miejsc. Dokładniej, założymy że
(czyli konfiguracje niemożliwe mają nieskończoną energię). Nie o to jednak chodzi. Ciekawe są rozkłady
Gibbsa, dla których fukcja energii ma specjalną postać związaną z topologią grafu ,,sąsiedztw”. Ograniczymy się do ważnej podklasy
markowowskich pól losowych (MPL), mianowicie do sytuacji gdy energia jest sumą ,,oddziaływań” lub ,,interakcji” między parami
miejsc sąsiadujących i składników zależnych od pojedynczych miejsc. Dokładniej, założymy że
| (13.3) |
dla pewnych funkcji ![]() i
i ![]() . Funkcja
. Funkcja ![]() opisuje ,,potencjał interakcji
pomiędzy
opisuje ,,potencjał interakcji
pomiędzy ![]() i
i ![]() ”, zaś
”, zaś ![]() jest wielkością związaną z ,,tendencją miejsca
jest wielkością związaną z ,,tendencją miejsca ![]() do przybrania koloru
do przybrania koloru ![]() .
Zwróćmy uwagę, że potencjał
.
Zwróćmy uwagę, że potencjał ![]() jest jednorodny (
jest jednorodny (![]() zależy tylko od ,,kolorów”
zależy tylko od ,,kolorów” ![]() ale nie od miejsc),
zaś
ale nie od miejsc),
zaś ![]() może zależeć zarówno od
może zależeć zarówno od ![]() jak i od
jak i od ![]() . W modelach fizyki statystycznej zazwyczaj
. W modelach fizyki statystycznej zazwyczaj
![]() jest jednorodnym ,,oddziaływaniem zewnętrznym” ale w modelach rekonstrukcji obrazów nie można tego zakładać.
jest jednorodnym ,,oddziaływaniem zewnętrznym” ale w modelach rekonstrukcji obrazów nie można tego zakładać.
Przykład 13.1 (Model Pottsa)
Niech ![]() będzie zbiorem skończonym i
będzie zbiorem skończonym i
Ta funkcja opisuje ,,tendencję sąsiednich miejsc do przybierania tego samego koloru”. Jeśli ![]() to preferowane są konfiguracje
złożone z dużych, jednobarwnych plam.
to preferowane są konfiguracje
złożone z dużych, jednobarwnych plam.
13.2. Generowanie markowowskich pól losowych
Użyteczność MPL w różnorodnych zastosowaniach związana jest z istnieniem efektywnych algorytmów symulacyjnych. Wszystko opiera się na próbniku Gibbsa i następującym prostym fakcie.
Twierdzenie 13.1 (Pełne rozkłady warunkowe dla MPL)
Jeżeli ![]() jest rozkładem Gibbsa z energią daną wzorem (13.3), to
jest rozkładem Gibbsa z energią daną wzorem (13.3), to
| (13.4) |
gdzie
| (13.5) |
![]() . Symbol
. Symbol ![]() oznacza konfigurację
powstałą z
oznacza konfigurację
powstałą z ![]() przez wpisanie koloru
przez wpisanie koloru ![]() w miejscu
w miejscu ![]() .
.
Dowód
Skorzystamy z elementarnej definicji prawdopodobieństwa warunkowego (poniżej piszemy ![]() ,
bo parametr
,
bo parametr ![]() jest ustalony):
jest ustalony):
| (13.6) |
Ponieważ otrzymany wynik zależy tylko od ![]() i
i ![]() , więc
, więc ![]() .
Ten wniosek jest pewną formą własności Markowa.
.
Ten wniosek jest pewną formą własności Markowa.
Zauważmy, że obliczenie ![]() jest łatwe, bo suma
jest łatwe, bo suma ![]() zawiera tylko tyle składników,
ile jest sąsiadów miejsca
zawiera tylko tyle składników,
ile jest sąsiadów miejsca ![]() . Obliczenie
. Obliczenie ![]() też jest łatwe, bo suma
też jest łatwe, bo suma ![]() zawiera tylko
zawiera tylko
![]() składników. Ale nawet nie musimy obliczać stałej normującej
składników. Ale nawet nie musimy obliczać stałej normującej ![]() żeby generować z rozkładu
żeby generować z rozkładu
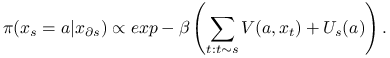 |
(13.7) |
Na tym opiera się implementacja próbnika Gibbsa. Wersję PG z ,,systemstycznym przeglądem miejsc” można zapisać tak:
| for |
| begin |
| Gen |
| |
| end |
13.3. Rekonstrukcja obrazów
Bayesowski model rekonstrukcji obrazów został zaproponowany w pracy Gemana i Gemana w 1987 roku. Potem zdobył dużą
popularność i odniósł wiele sukcesów. Model łączy idee zaczerpnięte ze statystyki bayesowskiej i fizyki
statystycznej. Cyfrową reprezentację obrazu utożsamiamy z konfiguracją kolorów na wierzchołkach
grafu, czyli z elementem przestrzeni ![]() , zdefiniowanej w Podrozdziale 13.1.
Przyjmijmy, że ,,idealny obraz”, czyli to co chcielibyśmy zrekonstruować jest konfiguracją
, zdefiniowanej w Podrozdziale 13.1.
Przyjmijmy, że ,,idealny obraz”, czyli to co chcielibyśmy zrekonstruować jest konfiguracją ![]() .
Niestety, obraz jest ,,zakłócony” lub ,,zaszumiony”. Możemy tylko obserwować konfigurację
.
Niestety, obraz jest ,,zakłócony” lub ,,zaszumiony”. Możemy tylko obserwować konfigurację ![]() reprezentującą
zakłócony obraz. Zbiór kolorów w obrazie
reprezentującą
zakłócony obraz. Zbiór kolorów w obrazie ![]() nie musi być identyczny jak w obrazie
nie musi być identyczny jak w obrazie ![]() . Powiedzmy, że
. Powiedzmy, że
![]() . Ważne jest to, że zniekształcenie modelujemy probabilistycznie przy pomocy rodziny rozkładów
warunkowych
. Ważne jest to, że zniekształcenie modelujemy probabilistycznie przy pomocy rodziny rozkładów
warunkowych ![]() .
Dodatkowo zakładamy, że obraz
.
Dodatkowo zakładamy, że obraz ![]() pojawia się losowo, zgodnie z rozkładem prawdopodobieństwa
pojawia się losowo, zgodnie z rozkładem prawdopodobieństwa ![]() . Innymi słowy,
,,idealny” obraz
. Innymi słowy,
,,idealny” obraz ![]() oraz ,,zniekształcony” obraz
oraz ,,zniekształcony” obraz ![]() traktujemy jako realizacje zmiennych losowych
traktujemy jako realizacje zmiennych losowych
![]() i
i ![]() ,
,
| (13.8) |
W ten sposób buduje się statystyczny model bayesowski, w którym
-
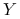 jest obserwowaną zmienną losową,
jest obserwowaną zmienną losową, -
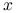 jest nieznanym parametrem traktowanym jako zmienna losowa
jest nieznanym parametrem traktowanym jako zmienna losowa 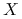 .
.
Oczywiście, ![]() gra rolę rozkładu a priori, zaś
gra rolę rozkładu a priori, zaś ![]() jest wiarogodnością.
Być może użycie literki
jest wiarogodnością.
Być może użycie literki ![]() na oznaczenie parametru jest niezgodne z tradycyjnymi oznaczeniami statystycznymi, ale
z drugiej strony jest wygodne. Wzór Bayesa mówi, że rozkład a posteriori jest następujący.
na oznaczenie parametru jest niezgodne z tradycyjnymi oznaczeniami statystycznymi, ale
z drugiej strony jest wygodne. Wzór Bayesa mówi, że rozkład a posteriori jest następujący.
| (13.9) |
Pomysł Gemana i Gemana polegał na tym, żeby modelować rozkład a priori ![]() jako MPL. Załóżmy,
że
jako MPL. Załóżmy,
że ![]() jest rozkładem Gibbsa,
jest rozkładem Gibbsa,
| (13.10) |
gdzie
| (13.11) |
Energia ,,a priori” zawiera tu tylko składniki reprezentujące oddziaływania między parami miejsc sąsiednich.
Funkcja ![]() zazwyczaj ma najmniejszą wartość dla
zazwyczaj ma najmniejszą wartość dla ![]() i rośnie wraz z ,,odległością” między
i rośnie wraz z ,,odległością” między ![]() i
i ![]() (jakkolwiek tę odległość zdefiniujemy). W ten sposób ,,nagradza” konfiguracje w których sąsiedznie miejsca są podobnie
pokolorowane. Im większy parametr
(jakkolwiek tę odległość zdefiniujemy). W ten sposób ,,nagradza” konfiguracje w których sąsiedznie miejsca są podobnie
pokolorowane. Im większy parametr ![]() , tym bardziej prawdopodobne są obrazy zawierające jednolite plamy kolorów.
, tym bardziej prawdopodobne są obrazy zawierające jednolite plamy kolorów.
Trzeba jeszcze założyć coś o ,,wiarogodności” ![]() . Dla uproszczenia opiszę tylko najprostszy model, w którym
kolor
. Dla uproszczenia opiszę tylko najprostszy model, w którym
kolor ![]() na obserwowanym obrazie zależy tylko od koloru
na obserwowanym obrazie zależy tylko od koloru ![]() na obrazie idealnym. Intuicyjnie znaczy to, że
,,zaszumienie” ma ściśle lokalny charakter. Matematycznie znaczy to, że
na obrazie idealnym. Intuicyjnie znaczy to, że
,,zaszumienie” ma ściśle lokalny charakter. Matematycznie znaczy to, że
| (13.12) |
(pozwolę sobie na odrobinę nieścisłości aby uniknąć nowego symbolu na oznaczenie ![]() ).
Zapiszemy teraz ,,wiarogodność”
).
Zapiszemy teraz ,,wiarogodność” ![]() w postaci zlogarytmowanej. Jeśli położymy
w postaci zlogarytmowanej. Jeśli położymy ![]() pamiętając, że
pamiętając, że ![]() jest w świecie bayesowskim ustalone, to otrzymujemy następujący wzór:
jest w świecie bayesowskim ustalone, to otrzymujemy następujący wzór:
| (13.13) |
gdzie
| (13.14) |
Okazuje się zatem, że rozkład a posteriori ma podobną postać do rozkładu a priori. Też jest
rozkładem Gibbsa, a różnica polega tylko na dodaniu składników reprezentujących oddziaływania zewnętrzne
![]() . Pamiętajmy przy tym, że
. Pamiętajmy przy tym, że ![]() jest w świecie bayesowskim ustalone.
W modelu rekonstrukcji obrazów ,,oddziaływania zewnętrzne” zależą od
jest w świecie bayesowskim ustalone.
W modelu rekonstrukcji obrazów ,,oddziaływania zewnętrzne” zależą od ![]() i ,,wymuszają podobieństwo”
rekonstruowanego obrazu do obserwacji. Z kolei ,,oddziaływania między parami” są odpowiedzialne za
wygładzenie obrazu. Lepiej to wyjaśnimy na przykładzie.
i ,,wymuszają podobieństwo”
rekonstruowanego obrazu do obserwacji. Z kolei ,,oddziaływania między parami” są odpowiedzialne za
wygładzenie obrazu. Lepiej to wyjaśnimy na przykładzie.
Przykład 13.2 (Losowe ,,przekłamanie koloru” i wygładzanie Pottsa)
Załóżmy, że ![]() jest naprawdę paletą kolorów, na przykład
jest naprawdę paletą kolorów, na przykład
![]() .
.
Przypuśćmy, że mechanizm losowego ,,przekłamania” polega na tym, że w każdym pikslu, kolor obecny w idealnym obrazie
![]() jest z prawdopodobieństwem
jest z prawdopodobieństwem ![]() niezmieniony, a z prawdopodobieństwem
niezmieniony, a z prawdopodobieństwem ![]() zmienia się na losowo wybrany inny kolor.
Tak więc zarówno
zmienia się na losowo wybrany inny kolor.
Tak więc zarówno ![]() jak i
jak i ![]() należą do tej samej przestrzeni
należą do tej samej przestrzeni ![]() ,
,
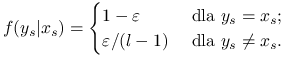 |
(13.15) |
Można za rozkład a priori przyjąć rozkład Pottsa z Przykładu 13.1. Rozkład a posteriori ma funkcję
energii daną następującym wzorem (z ![]() ):
):
| (13.16) |
Pierwszy składnik w tym wzorze pochodzi od rozkładu a priori (z modelu Pottsa) i ,,nagradza” konfiguracje w których dużo
sąsiednich punktów jest pomalowanych na ten sam kolor. Powoduje to, że obrazy ![]() składające się z jednolotych dużych ,,plam”
są preferowane. Drugi składnik pochodzi od obserwowanegj konfiguracji
składające się z jednolotych dużych ,,plam”
są preferowane. Drugi składnik pochodzi od obserwowanegj konfiguracji ![]() i jest najmniejszy dla
i jest najmniejszy dla ![]() . Powoduje to, ze
obrazy
. Powoduje to, ze
obrazy ![]() mało się różniące od
mało się różniące od ![]() są bardziej prawdopodobne. Rozkład a posteriori jest pewnym kompromisem
pomiędzy tymi dwoma konkurującymi składnikami. Parametr
są bardziej prawdopodobne. Rozkład a posteriori jest pewnym kompromisem
pomiędzy tymi dwoma konkurującymi składnikami. Parametr ![]() jest ,,wagą” pierwszego składnika i dlatego odgrywa rolę ,,parametru
wygładzającego”. Im większe
jest ,,wagą” pierwszego składnika i dlatego odgrywa rolę ,,parametru
wygładzającego”. Im większe ![]() tym odtwarzany obraz będzie bardziej regularny (a tym mnie będzie starał się upodobnić do
tym odtwarzany obraz będzie bardziej regularny (a tym mnie będzie starał się upodobnić do ![]() ).
I odwrotnie, małe
).
I odwrotnie, małe ![]() powoduje ściślejsze dopasowanie
powoduje ściślejsze dopasowanie ![]() do
do ![]() ale mniejszą ,,regularność”
ale mniejszą ,,regularność” ![]() .
.
Jeszcze lepiej to samo widać na przykładzie tak zwanego ,,szumu gaussowskiego”.
Przykład 13.3 (Addytywny szum gaussowski)
Załóżmy, że ![]() jest konfiguracją ,,poziomów szarości” czyli, powiedzmy,
jest konfiguracją ,,poziomów szarości” czyli, powiedzmy, ![]() . Mechanizm
losowego ,,zaszumienia” polega na tym, że zamiast poziomu szarości
. Mechanizm
losowego ,,zaszumienia” polega na tym, że zamiast poziomu szarości ![]() obserwujemy
obserwujemy ![]() .
Innymi słowy,
.
Innymi słowy,
| (13.17) |
Przestrzenią obserwaowanych konfiguracji ![]() jest tutaj (formalnie)
jest tutaj (formalnie) ![]() (faktycznie, raczej
(faktycznie, raczej ![]() ).
Rozkład a posteriori ma funkcję
energii daną następującym wzorem:
).
Rozkład a posteriori ma funkcję
energii daną następującym wzorem:
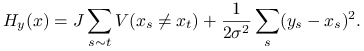 |
(13.18) |
Jeśli rozpatrujemy model ze skończoną liczbą poziomów szarości dla konfiguracji ![]() to można pierwszy składnik określić tak
jak w poprzednim przykładzie, czyli zapożyczyć z modelu Pottsa. Bardziej naturalne jest określenie
to można pierwszy składnik określić tak
jak w poprzednim przykładzie, czyli zapożyczyć z modelu Pottsa. Bardziej naturalne jest określenie
![]() w taki sposób, aby większe różnice pomiędzy poziomami
w taki sposób, aby większe różnice pomiędzy poziomami ![]() i
i ![]() były silniej karane. parametr
były silniej karane. parametr ![]() jest,
jak poprzednio, odpowiedzialny zaa stopień wygładzenia.
jest,
jak poprzednio, odpowiedzialny zaa stopień wygładzenia.




