Zagadnienia

14.1 Podstawowe określenia i oznaczenia
14.2 Regeneracja
14.3 Łańcuchy sprzężone i zbieżność rozkładów
- 14.3.1 Odległość pełnego wahania
- 14.3.2 Sprzęganie

14. Markowowskie Monte Carlo V. Elementarna teoria łańcuchów Markowa

14.1. Podstawowe określenia i oznaczenia

W tym rozdziale rozważamy jednorodny łańcuch Markowa $X_{0},X_{1},\ldots,X_{n},\ldots$ na skończonej przestrzeni stanów ${\cal X}=\{ 1,\ldots,d\}$ . Będziemy posługiwać się wygodną i zwięzłą notacją wektorowo-macierzową. Macierz przejścia o wymiarach $d\times d$ oznaczamy $P=\left(P(x,y)\right)_{{x,y\in{\cal X}}}$ . Rozkład początkowy utożsamiamy z wektorem wierszowym ${\xi}^{\top}=\big({\xi}(1),\ldots,{\xi}(x),\ldots,{\xi}(d)\big)$ . W dalszym ciągu, mówiąc o łańcuchu Markowa, będziemy mieli na myśli ustaloną macierz przejścia $P$ i dowolnie wybrany rozkład początkowy ${\xi}$ . Przyjmujemy oznaczenie $\mathbb{P}_{{\xi}}(\cdot)$ . W szczególności, $\mathbb{P}_{x}(\cdot)=\mathbb{P}(\cdot|X_{0}=x)$ , dla $x\in{\cal X}$ . Analogicznie będziemy oznaczali wartość oczekiwaną: $\mathbb{E}_{{\xi}}$ lub $\mathbb{E}_{x}$ . Zauważmy, że $\mathbb{P}(X_{{n+2}}=y|X_{n}=x)=\sum _{z}P(x,z)P(z,y)=P^{2}(x,y)$ . Ogólniej, macierz przejścia w $m$ krokach jest $m$ -tą potęgą macierzy $P$ :

$\mathbb{P}(X_{{n+m}}=y|X_{n}=x)=P^{m}(x,y).$

Rozkład brzegowy zmiennej losowej $X_{n}$ jest wektorem ${\xi}^{\top}P^{n}$ :

$\mathbb{P}(X_{n}=x)=\big({\xi}^{\top}P^{n}\big)(x).$

Z macierzą stochastyczną $P$ związany jest graf skierowany opisujący możliwe przejścia łańcucha. Jest to graf $({\cal X},{\cal E})$ , gdzie zbiorem wierzchołków jest przestrzeń stanów, zaś ${\cal E}\subseteq{\cal X}\times{\cal X}$ jest zbiorem takich par $(x,y)$ , że $P(x,y)>0$ . Pojęcia, o których teraz będziemy mówić, są związane tylko ze strukturą grafu, czyli z położeniem niezerowych elementów macierzy przejścia.

Mówimy, że stan $y$ jest osiągalny ze stanu $x$ , jeśli $x=y$ lub istnieje liczba naturalna $n\geq 1$ i ciąg stanów $x=x_{0},x_{1},x_{2},\ldots,x_{{n-1}},x_{n}=y$ taki, że $P(x_{{i-1}},x_{i})>0$ dla $i=1,\ldots,n$ . Równoważnie, $P^{n}(x,y)>0$ dla pewnego $n\geq 0$ . Będziemy stosowali oznaczenie ,, $x\to y$ ”.

Stany $x$ i $y$ komunikują się, co zapiszemy ,, $x\leftrightarrow y$ ”, jeśli $x\to y$ i $y\to x$ .

Stan $x$ jest istotny, jeśli dla każdego $y$ takiego, że $x\to y$ mamy $y\to x$ . W przeciwnym razie stan $x$ nazywamy nieistotnym. Stan $x$ jest więc nieistotny, jeśli istnieje stan $y$ do którego można przejść z $x$ , ale nie można wrócić do $x$ . Zbiór stanów istotnych oznaczymy przez ${\cal C}$ , zaś zbiór stanów nieistotnych przez ${\cal T}$ . Zbiór ${\cal C}$ jest (dla łańcucha o skończonej przestrzeni stanów) zawsze niepusty. Zbiór ${\cal T}$ może być pusty.

Jeśli $x\leftrightarrow y$ dla dowolnych $x,y\in{\cal X}$ , czyli wszystkie stany komunikują się, to łańcuch nazywamy nieprzywiedlnym. Oczywiście, wszystkie stany łańcucha nieprzywiedlnego są istotne, ${\cal X}={\cal C}$ . Łańcuch nieprzywiedlny nazywamy nieokresowym, jeśli dla dowolnych $x,y\in{\cal X}$ istnieje $n_{0}$ takie, że dla każdego $n\geq n_{0}$ mamy $P^{n}(x,y)$ . Wspomnijmy, że przyjęta przez nas definicja nieokresowości bywa formułowana w nieco inny, ale równoważny sposób. Dla naszych potrzeb wystarczy następujące proste spostrzeżenie: jeśli łańcuch jest nieprzywiedlny i $P(x,x)>0$ dla przynajmniej jednego stanu $x$ , to łańcuch jest nieokresowy. Łatwo zauważyć, że dla łańcucha nieprzywiedlnego i nieokresowego, dla dostatecznie dużych $n$ macierz $P^{n}$ ma wszystkie elementy niezerowe. Wynika to z faktu, że rozważamy łańcuchy ze skończoną przestrzenią stanów.

Jeśli $x\leftrightarrow y$ dla dowolnych $x,y\in{\cal C}$ , czyli wszystkie stany istotne komunikują się, to łańcuch nazywamy jednoklasowym. Łańcuch jednoklasowy może mieć niepusty zbiór stanów nieistotnych ${\cal T}$ . Łańcuch jednoklasowy możemy ,,przerobić” na nieprzywiedlny jeśli ograniczymy przestrzeń do stanów istotnych. Macierz $P_{{|{\cal C}}}=(P(x,y)_{{x,y\in{\cal C}}})$ jest, jak łatwo widzieć, stochastyczna.

Interesują nas głównie łańcuchy, które ,,zmierzają w kierunku położenia równowagi”. Aby uściślić co to znaczy ,,równowaga”, przypomnijmy pojęcie stacjonarności. Rozkład $\pi$ jest stacjonarny jeśli dla każdego stanu $y$ ,

$\pi(y)=\sum _{x}\pi(x)P(x,y).$

W notacji macierzowej: $\pi^{\top}=\pi^{\top}P$ . Stąd oczywiście wynika, że $\pi^{\top}=\pi^{\top}P^{n}$ .

Poniższy prosty fakt można uzasadnić na wiele sposobów. W następnym podrozdziale przytoczymy, wraz z dowodem, piękne twierdzenie Kaca (Twierdzenie 14.2), które implikuje Twierdzenie 14.1.

Twierdzenie 14.1

Jeśli łańcuch Markowa jest nieprzywiedlny, to istnieje dokładnie jeden rozkład stacjonarny $\pi$ , przy tym $\pi(x)>0$ dla każdego $x\in{\cal X}$ .

Z Twierdzenia 14.1 łatwo wynika następujący wniosek.

Wniosek 14.1

Jeśli łańcuch Markowa jest jednoklasowy, to istnieje dokładnie jeden rozkład stacjonarny $\pi$ , przy tym $\pi(x)>0$ dla każdego $x\in{\cal C}$ , czyli dla wszystkich stanów istotnych oraz $\pi(x)=0$ dla każdego $x\in{\cal T}$ , czyli dla stanów nieistotnych.

Uwaga 14.1

Podkreślmy stale obowiązujące w tym rozdziale założenie, że przestrzeń stanów jest skończona. To założenie jest istotne w Twierdzeniu 14.1 i to samo dotyczy dalszych rozważań. Istnieją co prawda odpowiedniki sformułowanych tu twierdzeń dla przypadku ogólnej przestrzeni stanów (nieskończonej, a nawet ,,ciągłej” takiej jak $\mathbb{R}^{d}$ ) ale wymagają one dodatkowych, niełatwych do sprawdzenia założeń. Przystępny i bardzo elegancki wykład teorii łańcuchów Markowa na ogólnej przestrzeni stanów można znaleźć w pracy Nummelina [17]. Przeglądowy artykuł Robertsa i Rosenthala [20] zawiera dużo dodatkowych informacji na ten temat. Obie cytowane prace koncentrują się na tych własnościach łańcuchów, które są istotne z punktu widzenia algorytmów Monte Carlo. Z kolei piękna książka Brémaud [4] ogranicza się do przestrzeni dyskretnych (skończonych lub przeliczalnych).

14.2. Regeneracja

Przedstawimy w tym podrozdziale konstrukcję, która prowadzi do łatwch i eleganckich dowodów twierdzeń granicznych. Podstawowa idea jest następująca. Wyróżnia się jeden ustalony stan, powiedzmy $z\in{\cal X}$ . W każdym momencie wpadnięcia w $z$ , następuje ,,odnowienie” i dalsza ewolucja łańcucha jest niezależna od przeszłości.

Niech, dla $z\in{\cal X}$ ,

$\qquad T^{z}=\min\{{n>0}:X_{n}=z\}.$

(14.1)

Przyjmujemy przy tym naturalną konwencję: $T^{z}=\infty$ , jeśli $X_{n}\not=z$ dla każdego $n\geq 1$ . Zmienna losowa $T^{z}$ jest więc czasem pierwszego dojścia do stanu $z$ . Jeśli założymy, że łańcuch startuje z punktu $z$ , to $T^{z}$ jest czasem pierwszego powrotu.

Lemat 14.1

Jeżeli łańcuch jest nieprzywiedlny, to istnieją stałe $c$ i $\gamma<1$ takie, że dla dowolnego rozkładu początkowego $\xi$ ,

$\mathbb{P}_{\xi}(T^{z}>n)\leqslant c\gamma^{n}.$

Dowód

Dla uproszczenia przyjmijmy dodatkowe założenie, że łańcuch jest nieokresowy. Wtedy dla dostatecznie dużych $k$ wszystkie elementy macierzy $P^{k}$ są niezerowe. Ustalmy $k$ i znajdźmy liczbę $\delta>0$ taką, że $P^{k}(x,z)\geq\delta$ dla wszystkich $x$ (jest to możliwe, bo łańcuch ma skończoną liczbę stanów). Dla dowolnego $n$ , dobierzmy takie $m$ , że $mk\leq n<(m+1)k$ . Mamy wówczas

$\begin{split}\mathbb{P}_{\xi}(T^{y}>n)&\leq\mathbb{P}_{\xi}(T^{y}>mk)\\ &\leq\mathbb{P}_{\xi}(X_{{0}}\not=z,X_{{k}}\not=z,\ldots,X_{{mk}}\not=z)\\ &=\sum _{{x_{0}\not=z,x_{1}\not=z,\ldots,x_{{m}}\not=z}}{\xi}(x_{0})P^{k}(x_{0},x_{1})\cdots P^{k}(x_{{m-1}},x_{m})\\ &\leq(1-\delta)^{m}\leq c\gamma^{n},\end{split}$

dla $\gamma=(1-\delta)^{{1/k}}$ i $c=(1-\delta)^{{-1}}$ .

W przypadku łańcucha okresowego dowód nieco się komplikuje i, choć nie jest trudny, zostanie pominięty.

∎

Wniosek 14.2

Dla łańcucha nieprzywiedlnego mamy $\mathbb{P}_{\xi}(T^{z}<\infty)=1$ , co więcej $\mathbb{E}_{\xi}T^{z}<\infty$ , co więcej $\mathbb{E}_{\xi}(T^{z})^{k}<\infty$ dla dowolnego $k$ , a nawet $\mathbb{E}_{\xi}\exp(\lambda T^{z})<\infty$ przynajmniej dla pewnych dostatecznie małych wartości $\lambda>0$ (w istocie dla $\lambda<-\log\gamma$ ).

Podamy teraz bardzo ciekawą interpretację rozkładu stacjonarnego, wykazując przy okazji jego istnienie (Twierdzenie 14.1). Ustalmy dowolnie wybrany stan $z$ . Udowodnimy, że średni czas, spędzony przez łańcuch w stanie $y$ pomiędzy wyjściem z $z$ i pierwszym powrotem do $z$ jest proporcjonalny do $\pi(y)$ , prawdopodobieństwa stacjonarnego.

Twierdzenie 14.2 (Kaca)

Załóżmy, że łańcuch jest nieprzywiedlny. Ustalmy $z\in{\cal X}$ i zdefiniujmy miarę $\alpha$ wzorem

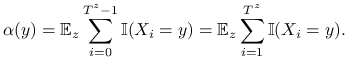$\alpha(y)=\mathbb{E}_{z}\sum _{{i=0}}^{{T^{z}-1}}\mathbb{I}(X_{i}=y)=\mathbb{E}_{z}\sum _{{i=1}}^{{T^{z}}}\mathbb{I}(X_{i}=y).$

Wtedy:

(i) Miara $\alpha$ jest stacjonarna, czyli $\alpha^{\top}P=\alpha$ .

(ii) Miara $\alpha$ jest skończona, $\alpha({\cal X})=\mathbb{E}_{z}(T^{z})=m<\infty$ .

(iii) Unormowana miara $\alpha/m=\pi$ jest jedynym rozkładem stacjonarnym.

Dowód

Dla uproszczenia będziemy pisali $T^{z}=T$ , $\mathbb{P}_{z}=\mathbb{P}$ i $\mathbb{E}_{z}=\mathbb{E}$ . Zauważmy, że

$\quad\begin{split}\alpha(x)&=\mathbb{E}\sum _{{i=0}}^{{T-1}}\mathbb{I}(X_{i}=x)=\mathbb{E}\sum _{{i=0}}^{{\infty}}\mathbb{I}(X_{i}=x,T>i)\\ &=\sum _{{i=0}}^{{\infty}}\mathbb{P}(X_{i}=x,T>i).\\ \end{split}$

Udowodnimy teraz (i). Jeśli $y\not=z$ , to

$\quad\begin{split}\sum _{x}\alpha(x)P(x,y)&=\sum _{x}\sum _{{i=0}}^{{\infty}}\mathbb{P}(X_{i}=x,T>i)P(x,y)\\ &=\sum _{{i=0}}^{{\infty}}\sum _{x}\mathbb{P}(X_{i}=x,T>i)P(x,y)\\ &=\sum _{{i=0}}^{{\infty}}\mathbb{P}(X_{{i+1}}=y,T>i+1)=\sum _{{i=1}}^{{\infty}}\mathbb{P}(X_{{i}}=y,T>i)\\ &=\alpha(y),\end{split}$

ponieważ $\mathbb{P}(X_{0}=y)=0$ , bo $\mathbb{P}(X_{0}=z)=1$ . Dla $y=z$ mamy z kolei

$\quad\begin{split}\sum _{x}\alpha(x)P(x,z)&=\sum _{x}\sum _{{i=0}}^{{\infty}}\mathbb{P}(X_{i}=x,T>i)P(x,z)\\ &=\sum _{{i=0}}^{{\infty}}\sum _{x}\mathbb{P}(X_{i}=x,T>i)P(x,z)\\ &=\sum _{{i=0}}^{{\infty}}\mathbb{P}(X_{{i+1}}=z,T=i+1)=\sum _{{i=1}}^{{\infty}}\mathbb{P}(T=i)\\ &=1=\alpha(z),\end{split}$

co kończy dowód (i).

Część (ii) jest łatwa. Równość

$\alpha({\cal X})=\sum _{y}\alpha(y)=\mathbb{E}T$

wynika wprost z definicji miary $\alpha$ . Fakt, że $m=\mathbb{E}T<\infty$ jest wnioskiem z Lematu 14.1.

Punkt (iii): istnienie rozkładu stacjonarnego

$\pi(y)=\frac{\alpha(y)}{m}.$

jest natychmiastowym wnioskiem z (i) i (ii). Jednoznaczność rozkładu stacjonarnego dla jest nietrudna do bezpośredniego udowodnienia. Pozostawiamy to jako ćwiczenie. W najbardziej interesującym nas przypadku łańcucha nieokresowego, jednoznaczność wyniknie też ze Słabego Twierdzenia Ergodycznego, które udowodnimy w następnym podrozdziale.

∎

Odnotujmy ważny wniosek wynikający z powyższego twierdzenia:

$\pi(z)=\frac{1}{\mathbb{E}_{z}(T^{z})}.$

Zjawisko odnowienia, czyli regeneracji pozwala sprowadzić badanie łańcuchów Markowa do rozpatrywania niezależnych zmiennych losowych, a więc do bardzo prostej i dobrze znanej sytuacji. Aby wyjaśnić to bliżej, zauważmy następującą oczywistą równość. Na mocy własności Markowa i jednorodności,

$\begin{split}&\mathbb{P}(X_{{n+1}}=x_{1},\ldots,X_{{n+k}}=x_{k}|T^{z}=n)\\ &\mathbb{P}(X_{{n+1}}=x_{1},\ldots,X_{{n+k}}=x_{k}|X_{n}=z)\\ &\qquad=\mathbb{P}_{z}(X_{{1}}=x_{1},\ldots,X_{{k}}=x_{k}).\end{split}$

Zatem warunkowo, dla $T^{z}=n$ , łańcuch ,,regeneruje się w momencie $n$ ” i zaczyna się zachowywać dokładnie tak, jak łańcuch który wystartował z punktu $z$ w chwili $0$ . Niezależnie od przeszłości! Ponieważ $z$ jest ustalone, będziemy odtąd pomijali górny indeks przy $T=T^{z}$ . Zdefiniujmy kolejne momenty odnowienia, czyli czasy odwiedzin stanu $z$ :

$\begin{split}\qquad T=T_{1}&=\min\{ n>0:X_{{n}}=z\},\\ T_{k}&=\min\{ n>T_{{k-1}}:X_{{n}}=z\}.\end{split}$

Momenty $0<T_{1}<\cdots<T_{k}<\cdots$ dzielą trajektorię łańcucha na następujące ,,losowe wycieczki”, czyli losowej długości ciągi zmiennych losowych:

$\underbrace{{X_{{0}}},\ldots,X_{{T_{1}-1}}}_{{T_{1}}}$ ,	$\underbrace{{X_{{T_{1}}}},\ldots,X_{{T_{2}-1}}}_{{T_{2}-T_{1}}}$ ,	$\underbrace{{X_{{T_{2}}}},\ldots,X_{{T_{3}-1}}}_{{T_{3}-T_{2}}}$ ,	$\ldots$
	$\;\uparrow$	$\;\uparrow$
	$X_{{T_{1}}}=z$	$X_{{T_{2}}}=z$	$\cdots$

Wycieczka zaczyna się w punkcie $z$ i kończy tuż przed powrotem do $z$ . Oznaczmy $k$ -tą wycieczkę symbolem $\Xi _{k}$ :

$\begin{split}\qquad\Xi=\Xi _{1}&=(X_{0},\ldots,X_{{T-1}},T),\\ \Xi _{k}&=(X_{{T_{{k-1}}}},\ldots,X_{{T_{{k}}-1}},T_{{k}}-T_{{k-1}})\\ \end{split}$

Z tego, co powiedzieliśmy wcześniej wynika, że wszystkie ,,wycieczki” są niezależne. Co więcej wycieczki $\Xi _{k}$ mają ten sam rozkład, z wyjątkiem być może początkowej, czyli $\Xi _{1}$ . Jeśli rozkład początkowy jest skupiony w punkcie $z$ , to również wycieczka $\Xi _{1}$ ma ten sam rozkład (0 jest wtedy momentem odnowienia).

Podejście regeneracyjne, czyli rozbicie łańcucha na niezależne wycieczki prowadzi do ładnych i łatwych dowodów PWL i CTG dla łańcuchów Markowa. Sformułujemy najpierw pewną wersję Mocnego Prawa Wielkich Liczb. Rozważmy funkcję $f$ o wartościach rzeczywistych, określoną na przestrzeni stanów. Przypomnijmy, że $\mathbb{E}_{\pi}f=\sum _{{x\in{\cal X}}}\pi(x)f(x)$ .

Twierdzenie 14.3 (Mocne Twierdzenie Ergodyczne)

Jeśli $X_{n}$ jest nieprzywiedlnym łańcuchem Markowa, to dla dowolnego rozkładu początkowego ${\xi}$ i każdej funkcji $f:{\cal X}\to\mathbb{R}$ ,

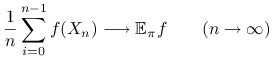${1\over n}\sum _{{i=0}}^{{n-1}}f(X_{n})\longrightarrow\mathbb{E}_{\pi}f\qquad(n\to\infty)$

z prawdopodobieństwem 1.

Dowód

Zdefiniujmy sumy blokowe:

$\begin{split}\qquad\Xi _{0}(f)&=\sum _{{i=0}}^{{T-1}}f(X_{i}),\\ \Xi _{k}(f)&=\sum _{{i=T_{k}}}^{{T_{{k+1}}-1}}f(X_{i}).\\ \end{split}$

Niech $N(n)=\max\{ k:T_{k}\leqslant n\}$ , czyli $T_{{N(n)}}$ jest ostatnią regeneracją przed momentem $n$ :

$0,\ldots,T_{1}-1,$	$T_{1},\ldots\ldots,$	$T_{{N(n)}},\ldots,n,$ $\ldots,T_{{N(n)+1}}-1,$	$T_{{N(n)+1}},\ldots$
	$\;\uparrow$	$\;\uparrow$ $\uparrow$	$\;\uparrow$
	$X=z$	$X=z$ $\bullet$	$X=z$

Oczywiście,

$\qquad T_{{N(n)}}\leqslant n<T_{{N(n)+1}}.$

(14.2)

Wiemy, że $\mathbb{E}_{z}T=m<\infty$ . Ponieważ $T_{k}$ jest sumą $k$ niezależnych zmiennych losowych (długości wycieczek) to wnioskujemy, ze $T_{k}/k\to m$ z prawdopodobieństwem 1, na mocy zwykłego Prawa Wielkich Liczb. Rzecz jasna, tak samo $T_{{k+1}}/k\to m$ . Podzielmy nierówność (14.2) stronami przez $N(n)$ i przejdźmy do granicy (korzystając z tego, że $N(n)\to\infty$ prawie na pewno). Twierdzenie o trzech ciągach pozwala wywnioskować, że

$\frac{N(n)}{n}\to\frac{1}{m}\:\textrm{ p.n.}$

Załóżmy teraz, że $f\geq 0$ i powtórzmy bardzo podobne rozumowanie dla sum

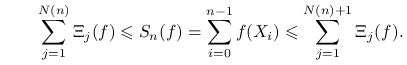$\qquad\sum _{{j=1}}^{{N(n)}}\Xi _{j}(f)\leqslant S_{n}(f)=\sum _{{i=0}}^{{n-1}}f(X_{i})\leqslant\sum _{{j=1}}^{{N(n)+1}}\Xi _{j}(f).$

(14.3)

Po lewej i po prawej stronie mamy sumy niezależnych składników $\Xi _{j}(f)$ . Korzystamy z PWL dla niezależnych zmiennych, dzielimy (14.3) stronami przez $N(n)$ i przejchodzimy do granicy. Otrzymujemy

$\frac{S_{n}(f)}{N(n)}\to{\mathbb{E}_{z}\Xi(f)}\:\textrm{ p.n.}$

a więc

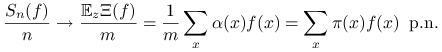$\frac{S_{n}(f)}{n}\to\frac{\mathbb{E}_{z}\Xi(f)}{m}=\frac{1}{m}\sum _{{x}}\alpha(x)f(x)=\sum _{{x}}\pi(x)f(x)\:\textrm{ p.n.}$

Ostatnia równość wynika z Twierdzenia Kaca. Przypomnijmy, że $\alpha(x)$ jest ,,średnim czasem spędzonym w stanie $x$ ” podczas pojedynczej wycieczki.

Jeśli funkcja $f$ nie jest nieujemna, to możemy zastosować rozkład $f=f^{+}-f^{-}$ i wykorzystać już udowodniony wynik.

∎

Na podobnej idei oparty jest ,,regeneracyjny” dowód Centralnego Twierdzenia Granicznego (istnieją też zupełnie inne dowody).

Twierdzenie 14.4 (Centralne Twierdzenie Graniczne)

Jeśli $X_{n}$ jest łańcuchem nieprzywiedlnym, to dla dowolnego rozkładu początkowego ${\xi}$ i każdej funkcji $f:{\cal X}\to\mathbb{R}$ ,

$\frac{1}{\sqrt{n}}\left(\sum _{{i=0}}^{{n-1}}[f(X_{{i}})-\mathbb{E}_{\pi}f]\right)\longrightarrow _{d}{\rm N}\big(0,{\sigma _{{\rm as}}^{{2}}(f)}\big),\quad(n\to\infty).$

Ponadto, dla dowolnego rozkładu początkowego $\xi$ zachodzi wzór (10.4), czyli $(1/n){\rm Var}_{\xi}\sum _{{i=0}}^{{n-1}}f(X_{{i}})$ $\to{\sigma _{{\rm as}}^{{2}}(f)}$ przy $n\to\infty$ .

Szkic dowodu

Trochę więcej jest tu technicznych zawiłości niż w dowodzie PWL, wobec tego zdecydowałem się pominąć szczegóły. W istocie, przedstawię tylko bardzo pobieżnie główną ideę. Bez straty ogólności załóżmy, że $\pi^{\top}f=0$ . Tak jak w dowodzie PWL, sumę $S_{n}(f)=\sum _{{i=0}}^{{n-1}}f(X_{i})$ przybliżamy sumą niezależnych składników, które odpowiadają całkowitym wycieczkom: $S_{n}(f)\simeq S_{{T_{{N(n)}}}}(f)=\sum _{{j=1}}^{{N(n)}}\Xi _{j}(f)$ . Ze zwykłego CTG dla niezależnych zmiennych o jednakowym rozkładzie otrzymujemy

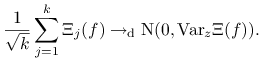$\frac{1}{\sqrt{k}}\sum _{{j=1}}^{{k}}\Xi _{j}(f)\to _{{\rm d}}{\rm N}(0,{\rm Var}_{z}\Xi(f)).$

Jeśli ,,podstawimy” w miejsce $k$ zmienną losową $N(n)$ i wykorzystamy fakt, że $N(n)\simeq n/m$ (PWL gwarantuje, że $N(n)/n\to 1/m$ ), to nie powinien dziwić następujący wniosek:

$\frac{1}{\sqrt{n}}S_{n}(f)\to _{{\rm d}}{\rm N}(0,{\rm Var}_{z}\Xi(f)/m).$

W ten sposób ,,otrzymujemy” tezę.

∎

Przytoczony powyżej rozumowanie daje ciekawe przedstawienie asymptotycznej wariancji:

${\sigma _{{\rm as}}^{{2}}(f)}={\rm Var}_{z}\Xi(f)/\mathbb{E}_{z}T.$

(14.4)

Istnieje wiele wyrażeń na asymptotyczną wariancję, przy tym różne wzory wymagają różnych założeń. Najbardziej znany jest wzór (10.5). Sformułujemy w jawny sposób potrzebne założenia, i przepiszemy ten wzór w postaci macierzowej. Najpierw musimy wprowadzić jeszcze parę nowych oznaczeń. Wygodnie będzie utożsamić funkcję $f$ z wektorem kolumnowym

$f=\left(\begin{array}[]{c}f(1)\cr\vdots\cr f(d)\cr\end{array}\right).$

Niech

$\Pi={\rm diag}\big(\pi(1),\ldots,\pi(d)\big),$

gdzie $\pi$ oznacza, jak zwykle, rozkład stacjonarny. Możemy teraz napisać

$\mathbb{E}_{{\pi}}f(X_{{0}})=\sum _{x}\pi(x)f(x)=\pi^{\top}f$

oraz

$\begin{split}{\rm Var}_{{\pi}}f(X_{{0}})&=\mathbb{E}_{{\pi}}f^{{2}}(X_{{0}})-[\ \mathbb{E}_{{\pi}}f(X_{{0}})\ ]^{{2}}\\ &=f^{\top}\Pi f-f^{{T}}\pi\pi^{{T}}f\\ &=f^{\top}\Pi(I-1\pi^{\top})f.\end{split}$

Podobnie,

$\begin{split}{\rm Cov}_{{\pi}}[\ f(X_{{0}}),f(X_{{n}})\ ]&=\mathbb{E}_{{\pi}}[\ f(X_{{0}})f(X_{{m}})\ ]-[\mathbb{E}_{{\pi}}f(X_{{0}})\ ]^{{2}}\\ &=f^{\top}\Pi P^{{n}}f-f^{\top}\pi\pi^{\top}f\\ &=f^{\top}\Pi(P^{{n}}-1\pi^{\top})f.\end{split}$

W powyższym wzorze, $I$ jest macierzą identycznościową, $1$ oznacza kolumnę jedynek. Łatwo sprawdzić, że $P^{n}-1\pi^{\top}=(P-1\pi^{\top})^{n}$ dla $n>0$ (ale nie dla $n=0$ ). Jeśli $P$ jest macierzą przejścia nieprzywiedlnego i nieokresowego łańcucha Markowa, to $P^{n}-1\pi^{\top}\to 0$ przy $n\to\infty$ na mocy Słabego Twierdzenia Ergodycznego. Stąd wynika zbieżność następujących szeregów:

$\begin{split} A&=\sum _{{n=0}}^{\infty}(P^{n}-1\pi^{\top}),\\ Z&=\sum _{{n=0}}^{\infty}(P-1\pi^{\top})^{n}=\left(I-P+1\pi^{\top}\right)^{{-1}}.\\ \end{split}$

Macierz $Z$ nazywamy macierzą fundamentalną. Ponieważ $P^{0}-1\pi^{\top}=I-1\pi^{\top}$ zaś $(P-1\pi^{\top})^{0}=I$ więc $Z=A+1\pi^{\top}$ .

Stwierdzenie 14.1 (Asymptotyczna wariancja)

Jeśli łańcuch jest nieprzywiedlny i nieokresowy, to zachodzi wzór (10.5), czyli

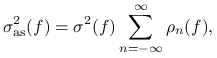${\sigma _{{\rm as}}^{{2}}(f)}=\sigma^{2}(f)\sum _{{n=-\infty}}^{\infty}\rho _{n}(f),$

gdzie $\sigma^{2}(f)={\rm Var}_{\pi}f(X_{0})$ i $\rho _{n}(f)={\rm corr}_{\pi}\left[f(X_{0}),f(X_{n})\right]$ , W postaci macierzowej asymptotyczna wariancja wyraża się następująco

${\sigma _{{\rm as}}^{{2}}(f)}=f^{\top}\big(2\Pi Z-\pi\pi^{\top}-\Pi\big)f=f^{\top}\big(2\Pi A+\pi\pi^{\top}-\Pi\big)f.$

Szkic dowodu

Załóżmy, że rozkładem początkowym jest $\pi$ i skorzystamy ze stacjonarności łańcucha:

$\begin{split}\frac{1}{n}{\rm Var}_{\pi}\left(\sum _{{i=0}}^{{n-1}}f(X_{i})\right)&=\frac{1}{n}\sum _{{i=0}}^{{n-1}}{\rm Var}_{\pi}(X_{i})+\frac{2}{n}\sum _{{i=0}}^{{n-1}}\sum _{{j=i}}^{{n-1}}{\rm Cov}_{\pi}(f(X_{i}),f(X_{j}))\\ &={\rm Var}_{\pi}f(X_{0})+2\sum _{{k=1}}^{{n-1}}\frac{n-k}{n}{\rm Cov}_{\pi}(f(X_{0}),f(X_{k}))\\ &\to{\rm Var}_{\pi}f(X_{0})+2\sum _{{k=1}}^{{\infty}}{\rm Cov}_{\pi}(f(X_{0}),f(X_{k})),\quad(n\to\infty).\end{split}$

Poprawność przejścia do granicy w ostatniej linijce wynika z elementarnego faktu, że dla dowolnego ciągu liczbowego $a_{n}$ mamy ${\lim _{{n\to\infty}}}\sum _{{k=1}}^{{n-1}}\frac{n-k}{n}a_{k}=\sum _{{k=1}}^{{\infty}}a_{k}$ , o ile szereg po prawej stronie równości jest zbieżny. To zaś, przy założeniu nieprzywiedlności i nieokresowości, wynika ze STE (skorzystaliśmy już z tego faktu uzasadniając poprawność definicji $Z$ i $A$ ).

Pokazaliśmy w ten sposób, że $(1/n){\rm Var}_{\pi}\sum _{{i=0}}^{{n-1}}f(X_{{i}})$ zmierza do granicy, która jest równa prawej stronie wzoru (10.5). Pominiemy uzasadnienie, że można zastąpić rozkład stacjonarny $\pi$ przez dowolny rozkład początkowy $\xi$ oraz że wzór (10.5) definiuje tę samą wielkość co (14.4).

Macierzowe wyrażenia ${\sigma _{{\rm as}}^{{2}}(f)}$ wynikają ze wzorów na kowariancje oraz z określenia macierzy $A$ i $Z$ .

∎

Zauważmy, że ani CTG ani PWL nie wymagały założenia o nieokresowości ale w 14.1 to założenie jest potrzebne.

Jak widać, asymptotyczna wariancja wyraża się w postaci formy kwadratowej ${\sigma _{{\rm as}}^{{2}}(f)}=f^{\top}Cf$ o współczynnikach

$\begin{split} C(x,y)&=\pi(x)A(x,y)+A(y,x)\pi(y)+\pi(x)\pi(y)-\pi(x)\mathbb{I}(x=y),\\ &=\pi(x)Z(x,y)+Z(y,x)\pi(y)-\pi(x)\pi(y)-\pi(x)\mathbb{I}(x=y).\end{split}$

Okazuje się, że ,,asymptotyczne obiążenie” estymatora ${\hat{\theta}_{{n}}}=(1/n)\sum _{{i=0}}^{{n-1}}f(X_{i})$ wartości oczekiwanej $\theta=\mathbb{E}_{\pi}f$ można napisać w postaci formy dwuliniowej $\xi^{\top}Af$ , gdzie $\xi$ jest rozkładem początkowym. Podsumowując,

$\begin{split}\qquad{\rm Var}_{\xi}({\hat{\theta}_{{n}}})&=\frac{1}{n}f^{\top}Cf+o\left(\frac{1}{n}\right),\\ \mathbb{E}_{\xi}{\hat{\theta}_{{n}}}-\theta f&=\frac{1}{n}\xi^{\top}Af+o\left(\frac{1}{n}\right).\end{split}$

Uzasadnienie drugiej części powyższego wzoru pozostawiam jako ćwiczenie. Stąd z łatwością otrzymujemy ważny wzór (10.6) z Rozdziału 10 (wyrażenie na błąd średniokwadratowy).

14.3. Łańcuchy sprzężone i zbieżność rozkładów

Dowód Słabego Twierdzenia Ergodycznego, który przedstawimy, opiera się na tak zwanym sprzęganiu (ang. coupling), czyli metodzie ,,dwóch cząstek”. Ta metoda, jak się okaże, nie tylko pozwala udowodnić zbieżność rozkładów prawdopodobieństwa, ale daje w wielu przypadkach bardzo dobre oszacowania szybkości zbieżności.

14.3.1. Odległość pełnego wahania

Najpierw zajmiemy się określeniem odległości między rozkładami. Dla naszych celów najbardziej przydatna będzie następująca metryka. Niech $\nu$ i $\lambda$ będą dwoma rozkładami prawdopodobieństwa na skończonej przestrzeni ${\cal X}$ . Odległość pełnego wahania pomiędzy $\nu$ i $\lambda$ określamy wzorem

$\qquad\|\nu-\lambda\| _{{\rm tv}}=\max _{{{\cal A}\subseteq{\cal X}}}|\nu({\cal A})-\lambda({\cal A})|.$

(14.5)

Jak zwykle, możemy utożsamić rozkład prawdopodobieństwa na ${\cal X}$ z funkcją, przypisującą prawdopodobieństwa pojedynczym punktom $x\in{\cal X}$ . Zauważmy, że

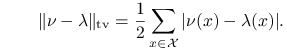$\qquad\|\nu-\lambda\| _{{\rm tv}}=\frac{1}{2}\sum _{{x\in{\cal X}}}|\nu(x)-\lambda(x)|.$

(14.6)

Istotnie, ponieważ rozpatrujemy dwie miary probabilistyczne, dla których $\nu({\cal X})=\lambda({\cal X})=1$ , więc $\|\nu-\lambda\|=\nu({\cal B})-\lambda({\cal B})$ dla ${\cal B}=\{ x:\nu(x)>\lambda(x)\}$ . Ale $\sum _{{x\in{\cal B}}}(\nu(x)-\lambda(x))=\sum _{{x\in{\cal X}\setminus{\cal B}}}(\lambda(x)-\nu(x))=\frac{1}{2}\sum _{{x\in{\cal X}}}|\nu(x)-\lambda(x)|$ .

Dla zmiennej losowej $X:\Omega\to{\cal X}$ napis $X\sim\nu$ będzie oznaczał fakt, że $X$ ma rozkład prawdopodobieństwa $\nu$ , czyli $\mathbb{P}(X=x)=\nu(x)$ ,

Lemat 14.2

Jeżeli $X,Y:\Omega\to{\cal X}$ są dwiema zmiennymi losowymi określonymi na tej samej przestrzeni probabilistycznej i $X\sim\nu$ i $Y\sim\lambda$ , to

$\|\nu-\lambda\| _{{\rm tv}}\leq\mathbb{P}(X\not=Y).$

Dowód

Niech $d=\mathbb{P}(X\not=Y)$ . Dla dowolnego ${\cal A}\subseteq{\cal X}$ mamy

$\nu({\cal A})=\mathbb{P}(X\in{\cal A})\leq\mathbb{P}(Y\in{\cal A})+\mathbb{P}(X\not=Y)=\lambda({\cal A})+d.$

Symetrycznie, $\nu({\cal A})\leq\lambda({\cal A})+d$ . Zatem $\|\nu-\lambda\| _{{\rm tv}}\leq d$ .

∎

Interesujące jest, że Lemat 14.2 daje się, w pewnym sensie, odwrócić. Co prawda, to nie będzie potrzebne w dowodzie Słabego Twioerdzenia Ergodycznego, ale później okaże się bardzo pomocne.

Lemat 14.3

Jeżeli $\nu$ i $\lambda$ są rozkładami prawdopodobieństwa na ${\cal X}$ , to istnieją zmienne losowe $X$ i $Y$ określone na tej samej przestrzeni probabilistycznej, takie, że $X\sim\nu$ i $Y\sim\lambda$ i

$\|\nu-\lambda\| _{{\rm tv}}=\mathbb{P}(X\not=Y).$

Dowód

Niech $\|\nu-\lambda\| _{{\rm tv}}=d$ . Bez straty ogólności możemy przyjąć, że $X$ i $Y$ są zmiennymi losowymi określonymi na przestrzeni probabilistycznej $\Omega={\cal X}\times{\cal X}$ . Należy podać łączny rozkład zmiennych losowych $X$ i $Y$ , czyli miarę probabilistyczną $\chi$ na ${\cal X}\times{\cal X}$ taką, że $\sum _{y}\chi(x,y)=\nu(x)$ , $\sum _{x}\chi(x,y)=\lambda(y)$ i $\sum _{x}\chi(x,x)=1-d$ .

Niech

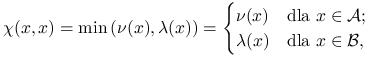$\chi(x,x)=\min\left(\nu(x),\lambda(x)\right)=\begin{cases}\nu(x)&\textrm{dla $x\in{\cal A}$;}\\ \lambda(x)&\textrm{dla $x\in{\cal B}$},\end{cases}$

gdzie ${\cal A}=\{ x:\nu(x)\leq\lambda(x)\}$ i ${\cal B}=\{ x:\nu(x)>\lambda(x)\}$ .

Mamy oczywiście $d=1-\sum _{x}\chi(x,x)$ i jest jasne, że tabelka łącznego rozkładu $\chi(x,y)=\mathbb{P}(X=x,Y=y)$ musi być postaci macierzy blokowej

$\qquad\begin{array}[]{r c c}\scriptstyle{x\in{\cal A}}\ \Big\{&D_{{\cal A}}&0\\ \scriptstyle{x\in{\cal B}}\ \Big\{&G&D_{{\cal B}}\\ &\underbrace{\phantom{--}}_{{y\in{\cal A}}}&\underbrace{\phantom{--}}_{{y\in{\cal B}}}\end{array},$

gdzie $D_{{\cal A}}$ i $D_{{\cal B}}$ są macierzami diagonalnymi. Pozostaje tylko odpowiednio ,,rozmieścić pozostałą masę prawdopodobieństwa” $d$ w macierzy $G$ . Możemy na przykład przyjąć, dla $x\in{\cal B}$ i $y\in{\cal A}$ ,

$\qquad\chi(x,y)=\frac{1}{d}\left(\nu(x)-\lambda(x)\right)\left(\lambda(y)-\nu(y)\right).$

Mamy wtedy $\sum _{{y\in{\cal A}}}\chi(x,y)=\nu(x)-\lambda(x)$ , więc $\sum _{{y}}\chi(x,y)=\nu(x)$ dla $x\in{\cal B}$ i podobnie $\sum _{{x}}\chi(x,y)=\lambda(x)$ dla $y\in{\cal A}$ . Określony przez nas rozkład łączny $\chi$ ma więc masę $1-d$ na przekątnej i żądane rozkłady brzegowe.

∎

14.3.2. Sprzęganie

Rozważmy ,,podwójny” łańcuch Markowa $(X_{n},X_{n}^{\prime})$ na przestrzeni stanów ${\cal X}\times{\cal X}$ . Przypuśćmy, że każda z dwóch ,,współrzędnych”, oddzielnie rozpatrywana, jest łańcuchem o macierzy przejścia $P$ . Mówiąc dokładniej, zakładamy, że

$\begin{split}&\mathbb{P}\left(X_{{n+1}}=y,X_{{n+1}}^{\prime}=y^{\prime}|X_{{n}}=x,X_{{n}}^{\prime}=x^{\prime},X_{{n-1}},X_{{n-1}}^{\prime},\ldots,X_{{0}},X_{{0}}^{\prime}\right)\\ &\qquad=\bar{P}\big((x,x^{\prime}),(y,y^{\prime})\big),\end{split}$

gdzie macierz przejścia $\bar{P}$ podwójnego łańcucha spełnia następujące warunki:

$\qquad\begin{split}&\sum _{{y^{\prime}}}\bar{P}\big((x,x^{\prime}),(y,y^{\prime})\big)=P(x,y)\quad\text{dla każdego }x^{\prime}\\ &\sum _{{y}}\bar{P}\big((x,x^{\prime}),(y,y^{\prime})\big)=P(x^{\prime},y^{\prime})\quad\text{dla każdego }x.\end{split}$

(14.7)

Widać, że $X_{0},X_{1},\ldots,X_{n},\ldots$ jest łańcuchem Markowa z prawdopodobieństwami przejścia $P$ i to samo można powiedzieć o $X_{0}^{\prime},X_{1}^{\prime},\ldots,X_{n}^{\prime},\ldots$ . Załóżmy ponadto, że od momentu, gdy oba łańcuchy się spotkają, dalej ,,poruszają się” już razem. Innymi słowy,

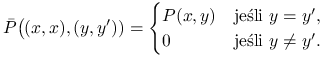$\bar{P}\big((x,x),(y,y^{\prime}))=\begin{cases}P(x,y)&\text{jeśli $y=y^{\prime}$},\\ 0&\text{jeśli $y\not=y^{\prime}$}.\end{cases}$

Nazwiemy konstrukcję takiej pary sprzęganiem łańcuchów (bardziej znany jest angielski termin coupling).

Oznaczmy przez $T$ moment spotkania się łańcuchów:

$\qquad T=\min\{{n>0}:X_{n}=X_{n}^{\prime}\}.$

(14.8)

Podstawową rolę odgrywa następujące spostrzeżenie:

$\qquad\|\mathbb{P}(X_{n}\in\cdot)-\mathbb{P}(X_{n}\in\cdot)\| _{{\rm tv}}\leqslant\mathbb{P}(X_{n}\not=X_{n}^{\prime})=\mathbb{P}(T>n).$

(14.9)

Jeśli teraz łańcuch $X_{n}^{\prime}$ ,,wystartuje” z rozkładu stacjonarnego, czyli $X_{0}\sim\pi$ to $X_{n}\sim\pi$ dla każdego $n$ i otrzymujemy

$\qquad\|\mathbb{P}(X_{n}\in\cdot)-\pi(\cdot)\| _{{\rm tv}}\leqslant\mathbb{P}(T>n).$

(14.10)

Aby udowodnić zbieżność $\mathbb{P}(X_{n}\in\cdot)\to\pi(\cdot)$ wystarczy skonstruować parę łańcuchów sprzężonych, które się spotkają z prawdopodobieństwem 1: $\mathbb{P}(T<\infty)=1$ . Możemy teraz udowodnić (10.1), przynajmniej dla łańcuchów na skończonej przestrzeni stanów.

Twierdzenie 14.5 (Słabe Twierdzenie Ergodyczne)

Jeśli łańcuch Markowa na skończonej przestrzeni stanów jest nieprzywiedlny i nieokresowy, to

$\|\mathbb{P}(X_{n}\in\cdot)-\pi(\cdot)\| _{{\rm tv}}\to 0.$

(14.11)

Dowód

Rozważmy parę łańcuchów sprzężonych, które poruszają się niezależnie aż do momentu spotkania.

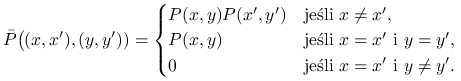$\bar{P}\big((x,x^{\prime}),(y,y^{\prime}))=\begin{cases}P(x,y)P(x^{\prime},y^{\prime})&\text{jeśli $x\not=x^{\prime}$},\\ P(x,y)&\text{jeśli $x=x^{\prime}$ i $y=y^{\prime}$},\\ 0&\text{jeśli $x=x^{\prime}$ i $y\not=y^{\prime}$}.\end{cases}$

(14.12)

Żeby pokazać, że $\mathbb{P}(T<\infty)=1$ wystarczy zauważyć, że do przed momentem spotkania, łańcuch podwójny ewoluuje zgodnie z prawdopodobieństwami przejścia

$\tilde{P}\big((x,x^{\prime}),(y,y^{\prime}))=P(x,y)P(x^{\prime},y^{\prime}).$

(14.13)

Łańcuch odpowiadający $\tilde{P}$ jest nieprzywiedlny. Istotnie, możemy znaleźć takie $n_{0}$ , że dla $n\geqslant n_{0}$ wszystkie elementy macierzy $P^{n}$ są niezerowe. Stąd $P^{n}\big((x,x^{\prime}),(y,y^{\prime}))=P^{n}(x,y)P^{n}(x^{\prime},y^{\prime})>0$ dla dowolnych $x,x^{\prime},y,y^{\prime}$ . Wystarczy teraz powołać się na Wniosek 14.2: podwójny łańcuch z prawdopodobieństwem 1 prędzej czy później dojdzie do każdego punktu przestrzeni ${\cal X}\times{\cal X}$ , a zatem musi dojść do ,,przekątnej” $\{(x,x):x\in{\cal X}\}$ .

∎

Uwaga 14.2

W dowodzie Twierdzenia 14.5 wykorzystaliśmy w istotny sposób nieokresowość macierzy przejścia $P$ (dla pojedynczego łańcucha), choć to mogło nie być wyraźnie widoczne. Jeśli $P$ jest nieprzywiedlna ale okresowa, wtedy $\tilde{P}$ jest nieprzywiedlna. Na przykład, niech ${\cal X}=\{ 0,1\}$ i

$P=\begin{pmatrix}0&1\\ 1&0\end{pmatrix}.$

Wtedy, oczywiście, $\tilde{P}^{n}((0,0),(0,1))=0$ bo $P^{n}(0,0)=0$ dla nieparzystych $n$ zaś $P^{n}(0,1)=0$ dla parzystych $n$ .

Ten sam trywialny przykład pokazuje, że dla łańcuchów okresowych teza Słabego Twierdzenia Ergodycznego nie jest prawdziwa.

W istocie, przytoczony przez nas dowód Twierdzenia 14.5 daje nieco więcej, niż tylko zbieżność rozkładów. Z Wniosku 14.2 wynika, że

$\|\mathbb{P}(X_{n}\in\cdot)-\pi(\cdot)\| _{{\rm tv}}\leqslant c\gamma^{n}$

(14.14)

dla pewnych stałych $c<\infty$ i $\gamma<1$ . Dla naszych celów takie ogólnikowe stwierdzenie nie jest wystarczające. Skupimy się na przykładach łańcuchów używanych w algorytmach MCMC, dla których znajdziemy jawne oszacowania, z konkretnymi stałymi. Zobaczymy, że użycie niezależnych kopii łańcucha w dowodzie Twierdzenia 14.5, wzór (14.12) jest konstrukcją dalece nieoptymalną. W wielu przykładach istnieją łańcuchy sprzężone znacznie szybciej ,,zmierzające do spotkania”.

Przykład 14.1 (Błądzenie po kostce)

Niech ${\cal X}=\{ 0,1\}^{n}$ i $\pi={\rm U}({\cal X})$ , czyli $\pi(x)=1/2^{n}$ dla każdego $x$ . Rozważmy łańcuch Markowa $X_{n}$ , którego krok polega na wylosowaniu jednej, losowo wybranej współrzędnej z rozkładu $(1/2,1/2)$ na zbiorze $\{ 0,1\}$ i pozostawieniu pozostałych współrzędnych bez zmian. Formalnie,

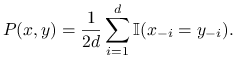$P(x,y)=\frac{1}{2d}\sum _{{i=1}}^{d}\mathbb{I}(x_{{-i}}=y_{{-i}}).$

Jest to zatem ,,losowe błądzenie” wzdłuż krawędzi $n$ -wymiarowej kostki lub inaczej próbnik Gibbsa. Rzecz jasna, dokładne genrowanie z rozkładu jednostajnego na kostce jest łatwe i nie ptrzebujemy do tego łańcuchów Markowa, ale nie o to teraz chodzi. Chcemy zilustrować jak metoda sprzęgania pozwala oszacować szybkość zbieżności łańcucha na możliwie prostym przykładzie. Skonstruujmy parę łańcuchów sprzężonych w taki sposób: wybieramy współrzędną $i$ oraz losujemy jej nową wartość z rozkładu $(1/2,1/2)$ po czym zmieniamy w ten sam sposób obie kopie. Formalnie,

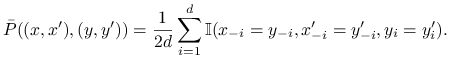$\bar{P}((x,x^{\prime}),(y,y^{\prime}))=\frac{1}{2d}\sum _{{i=1}}^{d}\mathbb{I}(x_{{-i}}=y_{{-i}},x_{{-i}}^{\prime}=y_{{-i}}^{\prime},y_{i}=y_{i}^{\prime}).$

Jest jasne, że to jest poprawny coupling (sprzęganie), to znaczy spełnione są równania (14.12). Spotkanie obu kopii nastąpi najpóźniej w momencie gdy każda ze współrzędnych zostanie wybrana przynajmniej raz. Zatem

$\mathbb{P}(T>n)\leq\left(1-\frac{1}{d}\right)^{n}.$

Nie trudno wyobrazić sobie, że dla niezależnego couplingu określonego wzorem (14.12), czasu oczekiwania na spotkanie obu kopii jest na ogół dużo, dużo dłuższy.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Symulacje stochastyczne i metody Monte Carlo

Zagadnienia

14. Markowowskie Monte Carlo V. Elementarna teoria łańcuchów Markowa

14.1. Podstawowe określenia i oznaczenia

Twierdzenie 14.1

Wniosek 14.1

Uwaga 14.1

14.2. Regeneracja

Lemat 14.1

Dowód

Wniosek 14.2

Twierdzenie 14.2 (Kaca)

Dowód

Twierdzenie 14.3 (Mocne Twierdzenie Ergodyczne)

Dowód

Twierdzenie 14.4 (Centralne Twierdzenie Graniczne)

Szkic dowodu

Stwierdzenie 14.1 (Asymptotyczna wariancja)

Szkic dowodu

14.3. Łańcuchy sprzężone i zbieżność rozkładów

14.3.1. Odległość pełnego wahania

Lemat 14.2

Dowód

Lemat 14.3

Dowód

14.3.2. Sprzęganie

Twierdzenie 14.5 (Słabe Twierdzenie Ergodyczne)

Dowód

Uwaga 14.2

Przykład 14.1 (Błądzenie po kostce)