Zagadnienia

2.1 Początki
2.2 Ćwiczenia

2. Podstawy R i ćwiczenia komputerowe

Oczekuję, że Czytelnik uruchomił pakiet (lub ,,otoczenie”, environment) R. Nie zakładam żadnej wstępnej znajomości tego języka programowania. Oczywiście, podstaw programowania w R można się nauczyć z odpowiednich źródeł. Ale prawdę mówiąc, prostych rzeczy można się szybko domyślić i zacząć zabawę natychmiast.

2.1. Początki

Przykład 2.1 (Rozkład prawdopodobieństwa i próbka losowa)

Wylosujmy ,,próbkę” średniego rozmiaru, powiedzmy $n=100$ z rozkładu normalnego ${\rm N}(0,1)$ :

> n <- 100
> X <- rnorm(n)
> X

(aby przyjrzeć się funkcji rnorm, napiszmy ?rnorm). Wektor X zawiera ,,realizacje” niezależnych zmiennych losowych $X_{1},\ldots,X_{{100}}$ . Możemy obliczyć średnią $\bar{X}=n^{{-1}}\sum _{{i=1}}^{{n}}X_{{i}}$ i wariancję próbkową $\bar{X}=(n-1)^{{-1}}\sum _{{i=1}}^{{n}}(X_{{i}}-\bar{X})^{2}$ . Jakich wyników oczekujemy? Zobaczmy:

> mean(X)
> var(X)

Porównajmy kwantyl empiryczny rzędu, powiedzmy $p=1/3$ , z teoretycznym:

> quantile(X,p)
> qnorm(p)

Możemy powtórzyć nasze ,,doświadczenie losowe” i zobaczyć jakie są losowe fluktuacje wyników. Warto wykonać nasz mini-programik jeszcze raz, albo parę razy. Teraz sprobujmy ,,zobaczyć” próbkę. Najlepiej tak:

> hist(X,prob=TRUE) ( proszę się dowiedzieć co znaczy parametr `prob' ! )
> rug(X)

Możemy łatwo narysować wykres gęstości. Funkcja obliczająca gęstość $\varphi$ rozkładu ${\rm N}(0,1)$ nazywa się dnorm, a curve jest funkcją rysującą wykresy.

> curve(dnorm(x),col="blue",add=TRUE)

(nawiasem mówiąc, zachęcam początkujących pRobabilistów do oznaczania wygenerowanych wektorów losowych dużymi literami, np. X, a deterministycznych zmiennych i wektorów – małymi, np. x, podobnie jak na rachunku prawdopodobieństwa).

Podobnie, możemy porównać dystrybuantę empiryczną z prawdziwą dystrybuantą $\Phi$ . Funkcja obliczająca dystrybuantę empiryczną nazywa się ecdf, zaś dystrybuantę rozkładu ${\rm N}(0,1)$ – pnorm.

> plot(ecdf(X))
> curve(pnorm(x),from=xmin,to=xmax,col="blue",add=TRUE)

Test Kołmogorowa-Smirnowa oblicza maksymalną odległość $D=\sum _{x}|\hat{F}_{n}(x)-F(x)|$ , gdzie $\hat{F}_{n}$ jest dystrybuantą empiryczną i $F=\Phi$ .

> ks.test(X,pnorm,exact=TRUE)

Przypomnijmy sobie z wykładu ze statystyki, co znaczy podana przez test $p$ -wartość. Jakiego wyniku ,,spodziewaliśmy się”?

Jest teraz dobra okazja, aby pokazać jak się symulacyjnie bada rozkład zmiennej losowej. Przypuśćmy, że interesuje nas rozkład prawdopodobieństwa $p$ -wartości w przeprowadzonym powyżej doświadczeniu (polegającym na wylosowaniu próbki $X$ i przeprowadzeniu testu KS). Tak naprawdę powinniśmy znać odpowiedź bez żadnych doświadczeń, ale możemy udawać niewiedzę i symulować.

Przykład 2.2 (Powtarzanie doświadczenia symulacyjnego)

Symulacje polegają na powtórzeniu całego doświadczenia wiele razy, powiedzmy $m=10000$ razy, zanotowaniu wyników i uznaniu powstałego rozkładu empirycznego za przybliżenie badanego rozkładu prawdopodobieństwa. Bardzo ważne jest zrozumienie różnej roli jaką pełni tu $n$ (rozmiar próbki w pojedynczym doświadczeniu, a więc ,,parametr badanego zjawiska”) i $m$ (liczba powtórzeń, która powinna być możliwie największa aby zwiększyć dokładność badania symulacyjnego). Następujący progarmik podkreśla logiczną konstrukcję powtarzanego doświadczenia:

> m <- 10000
> n <- 100
>
> # Przygotowujemy wektory w którym zapiszemy wyniki:
> D <- c()
> P <- c()
>
> for (i in 1:m)
> {
> X <- rnorm(n)
> Test <- ks.test(X,pnorm,exact=TRUE)
> D[i] <- Test$statistic
> P[i] <- Test$p.value
> } # koniec pętli for
>
> # Analizujemy wyniki:
> hist(D, prob=TRUE)
> hist(P, prob=TRUE)

Co prawda powyższy programik spełnia swoją rolę, jednak struktura pakiektu R jest dostosowana do innego stylu pisania programów. Zamiast pętli for zalecane jest używanie funkcji które powtarzają pewne operacje i posługiwanie się, kiedykolwiek to możliwe, całymi wektorami a nie pojedynczymi komponentami. Poniższy fragment kodu zastępuje pętlę for

> DiP <- replicate(m, ks.test(rnorm(n),pnorm,exact=TRUE)[1:2]))
>
> DiP <- t(DiP) # transpozycja macierzy ułatwia oglądanie wyników
> D <- as.numeric((DiP)[,1]) # pierwsza kolumna macierzy
> P <- as.numeric((DiP)[,2]) # druga kolumna macierzy
> # obiekty typu ,,list'' przerobimy na wektory liczbowe:
> D <- as.numeric(D); P <- as.numeric(D)

Symulacje dają okazję ,,namacalnego” przedstawienia twierdzeń probabilistycznych (i nie tylko twierdzeń, ale także stwierdzeń, przypuszczeń prawdziwych lub fałszywych).

Przykład 2.3 (Mocne Prawo Wielkich Liczb)

Wylosujmy próbkę z ,,jakiegoś” rozkładu prawdopodobieństwa. Weźmy na przykład niezależne zmienne o rozkładzie wykładniczym, $X_{1},\ldots,X_{n},\ldots{\rm Ex}(2)$ . Obliczmy średnie empiryczne

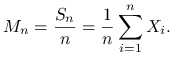$M_{n}=\frac{S_{n}}{n}=\frac{1}{n}\sum _{{i=1}}^{{n}}X_{i}.$

Zróbmy wykres ciągu średnich $S_{1}/1,S_{2}/2,\ldots,S_{n}/n,\ldots$ .

> nmax <- 1000 # komputerowy odpowiednik ,, $n\to\infty$ ''
> n <- (1:nmax)
> lambda <- 2 > X <- rexp(nmax,rate=lambda)
> S <- cumsum(X) # ciąg narastających sum
> M <- S/n # działania w R (np. dzielenie) są wykonywane ,,po współrzędnych''
> plot(n,M,type="l") # ,,zaklęcie'' type="l" powoduje narysowanie łamanej

Teraz spóbujmy podobne doświadczenie zrobić dla zmiennych $X_{i}=1/U_{i}-1$ , gdzie $U_{i}\sim{\rm U}(0,1)$ ( $X_{i}$ są próbką z tak zwanego rozkładu Pareto).

> # potrzebujemy dużej próbki, żeby się zorientować, co się dzieje...
> nmax <- 100000
> n <- (1:nmax)
> X <- 1/runif(nmax)-1
> M <- cumsum(X)/n
> plot(log(n),M,type="l") # i zrobimy wykres w skali logarytmicznej

Przykład 2.4 (Centralne Twierdzenie Graniczne)

CTG jest jednym ze ,,słabych” twierdzeń granicznych rachunku prawdopodobieństwa, to znaczy dotyczy zbieżności rozkładów. Symulacyne ,,sprawdzenie” lub ilustracja takich twierdzeń wymaga powtarzania doświadczenia wiele razy, podobnie jak w Przykładzie 2.2. Pojedyncze doświadczenie polega na obliczeniu sumy

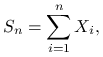$S_{n}=\sum _{{i=1}}^{{n}}X_{i},$

gdzie $X_{1},\ldots,X_{n}$ jest próbką z ,,jakiegoś” rozkładu prawdopodobieństwa i $n$ jest ,,duże”. Weźmy na przykład niezależne zmienne o rozkładzie wykładniczym, jak w Przykładzie 2.3.

> m <- 10000
> n <- 100
> lambda <- 2
> S <- replicate(m, sum(rexp(n,rate=lambda)))
> hist(S,prob=TRUE)
> curve(dnorm(x,mean=n/lambda,sd=sqrt(n)/lambda),col="blue",add=TRUE)
> # wydaje się na podstawie obrazka, że dopasowanie jest znakomite
> ks.test(S,pnorm,mean=n/lambda,sd=sqrt(n)/lambda)
> # ale test Kołmogorowa-Smirnowa ,,widzi'' pewne odchylenie od rozkładu normalnego >

Chciałbym podkreślić raz jeszcze różnicę pomiędzy metodologią sprawdzania ,,mocnego” twierdzenia granicznego w Przykładzie 2.3 i ,,słabego” w Przykładzie 2.4. W pierwszym przypadku chcieliśmy zobrazować zbieżność ciągu zmiennych losowych, a w drugim – zbieżność ciągu rozkładów prawdopodobieństwa.

2.2. Ćwiczenia

Ćwiczenie 2.1

Wyjaśnić dlaczego w Przykładzie 2.4 nie musieliśmy (choć mogliśmy) rozpatrywać unormowanych zmiennych losowych

$\frac{S_{n}-n\mu}{\sqrt{n}\sigma},$

gdzie $\mu=\mathbb{E}X_{1}$ i $\sigma^{2}={\rm Var}X_{1}$ .

Ćwiczenie 2.2

W Przykładzie 2.4 znany jest dokładny rozkład prawdopodobieństwa sumy $S_{n}$ . Co to za rozkład? Sprawdzić symulacyjnie zgodność z tym rozkładem.

Ćwiczenie 2.3

Przeprowadzić podobne doświadczenie jak w Przykładzie 2.4 (CTG), dla $n=12$ i $X_{i}\sim{\rm U}(0,1)$ . Skomentować wynik.

Ćwiczenie 2.4

Przeprowadzić podobne doświadczenie jak w Ćwiczeniu 2.3, ale zastępując sumę przez medianę dla $n=13$ i $X_{i}\sim{\rm U}(0,1)$ . Wypróbować przybliżenie normalne (jeśli teoretyczna wartość wariancji mediany nie jest znana, można zastąpić ją przez przybliżenie empiryczne). Skomentować wynik.

Ćwiczenie 2.5

W Ćwiczeniu 2.3, znany jest dokładny rozkład prawdopodobieństwa mediany. Co to za rozkład? Sprawdzić symulacyjnie zgodność z tym rozkładem. Można wziąć mniejsze, nieparzyste $n$ . Dlaczego nieparzyste?

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Symulacje stochastyczne i metody Monte Carlo