Zagadnienia

3.1 Przykłady
3.2 Metoda przekształceń
- 3.2.1 Odwrócenie dystrybuanty
3.3 Metoda eliminacji
- 3.3.1 Ogólny algorytm
- 3.3.2 Eliminacja w R
3.4 Metoda kompozycji

3. Generowanie zmiennych losowych I. Ogólne metody

3.1. Przykłady

Moje wykłady ograniczają się do zagadnień leżących w kompetencji rachunku prawdopodobieństwa i statystyki. U podstaw symulacji stochastycznych leży generowanie ,,liczb pseudo-losowych”, naśladujących zachowanie zmiennych losowych o rozkładzie jednostajnym. Jak to się robi, co to jest ,,pseudo-losowość”, czym się różni od ,,prawdziwej losowości”? To są fascynujące pytania, którymi zajmuje się: teoria liczb, teoria (chaotycznych) układów dynamicznych oraz filozofia. Dyskusja na ten temat przekracza ramy tych wykładów. Z punktu widzenia użytkownika, ,,liczby losowe” są bardzo łatwo dostępne, bo ich generatory są wbudowane w systemy komputerowe. Przyjmę pragmatyczny punkt widzenia i zacznę od następującego założenia.

Założenie 3.1

Mamy do dyspozycji potencjalnie nieskończony ciąg niezależnych zmiennych losowych $U_{1},\ldots\, U_{n}\ldots$ o jednakowym rozkładzie ${\rm U}(0,1)$ .

W języku algorytmicznym: przyjmujemy, że każdorazowe wykonanie instrukcji zapisanej w pseudokodzie

Gen $U\sim{\rm U}(0,1)$

wygeneruje kolejną (nową) zmienną $U_{n}$ . Innymi słowy, zostanie wykonane nowe, niezależne doświadczenie polegające na wylosowaniu przypadkowo wybranej liczby z przedziału $]0,1[$ .

Przykład 3.1

Wykonanie pseudokodu

for $i=1$ to $10$

begin

Gen $U\sim{\rm U}(0,1)$

write $U$

end

da, powiedzmy, taki efekt:

0.32240106 0.38971803 0.35222521 0.22550039 0.04162166
0.13976025 0.16943910 0.69482111 0.28812341 0.58138865

Nawiasem mówiąc, rzeczywisty kod w R, który wyprodukował nasze 10 liczb losowych był taki:

U <- runif(10);U

Język R jest zwięzły i piękny, ale nasz pseudokod ma pewne walory dydaktyczne.

Zajmiemy się teraz pytaniem, jak ,,wyprodukować” zmienne losowe o różnych rozkładach, wykorzystując zmienne $U_{1},U_{2},\ldots$ . W tym podrozdziale pokażę kilka przykładów, a w następnym przedstawię rzecz nieco bardziej systematycznie.

Przykład 3.2 (Rozkład Wykładniczy)

To jest wyjątkowo łatwy do generowania rozkład – wystarczy taki algorytm:

Gen $U$ ; $X:=-\frac{1}{\lambda}\ln U$

Na wyjściu, $X\sim{\rm Ex}(\lambda)$ . Żeby się o tym przekonać, wystarczy obliczyć dystrybuantę tej zmiennej losowej: $\mathbb{P}(X\leq x)=\mathbb{P}(-\frac{1}{\lambda}\log U\leq x)=\mathbb{P}(U\geq{\rm e}^{{-\lambda x}})=1-{\rm e}^{{-\lambda x}}$ . Jest to najprostszy przykład ogólnej metody ,,odwracania dystrybuanty”, której poświęcę następny podrozdział.

Przykład 3.3 (Generacja rozkładu normalnego)

Zmienna losowa

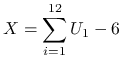$X=\sum\limits _{{i=1}}^{{12}}U_{1}-6$

ma w przybliżeniu standardowy rozkład normalny ${\rm N}(0,1)$ . Wynika to z Centralnego Twiedzenia Granicznego (jeśli uznamy, że liczba $12$ jest dostatecznie bliska $\infty$ ; zauważmy, że $\mathbb{E}X=0$ i ${\rm Var}X=1$ ). Oczywiście, w czasach szybkich komputerów ta przybliżona metoda zdecydowanie nie jest polecana. Jest natomiast pouczające zbadać (symulacyjnie!) jak dobre jest przybliżenie. Faktycznie bardzo trudno odróżnić próbkę $X_{1},\ldots,X_{n}$ wyprodukowaną przez powyższy algorytm od próbki pochodzącej dokładnie z rozkłdu ${\rm N}(0,1)$ (chyba, że $n$ jest ogromne).

Przykład 3.4 (Algorytm Boxa-Müllera)

Oto, dla porównania, bardziej współczesna – i całkiem dokładna metoda generowania zmiennych o rozkładzie normalnym.

Gen $U_{1};\;\Theta:=2\pi U_{1}$ ,

Gen $U_{2};\; R:=\sqrt{-2\ln U_{2}},$

Gen $X:=R\cos\Theta$ ; $Y:=R\sin\Theta$

Na wyjściu obie zmienne $X$ i $Y$ mają rozkład ${\rm N}(0,1)$ i w dodatku są niezależne. Uzasadnienie poprawności algorytmu Boxa-Müllera opiera się na dwu faktach: zmienna $R^{2}=X^{2}+Y^{2}$ ma rozkład $\chi^{2}(2)={\rm Ex}(1/2)$ , zaś kąt $\Theta$ między osią i promieniem wodzącym punktu $(X,Y)$ ma rozkład ${\rm U}(0,2\pi)$ .

Ciekawe, że łatwiej jest generować zmienne losowe normalne ,,parami”.

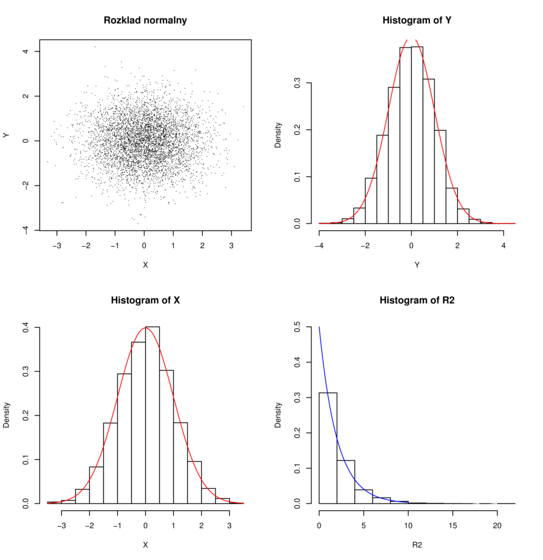
Doświadczenie, polegające na wygenerowaniu zmiennych losowych $X$ i $Y$ powtórzyłem 10000 razy. Na Rysunku 3.1 widać 10000 wylosowanych w ten sam sposób i niezależnie punktów $(X,Y)$ , histogramy i gęstości brzegowe $X$ i $Y$ (każda ze współrzędnych ma rozkłd ${\rm N}(0,1)$ ) oraz histogram i gęstość $R^{2}=X^{2}+Y^{2}$ ( rozkład wykładniczy ${\rm Ex}(1/2)$ ).

Histogram jest ,,empirycznym” (może w obecnym kontekście należałoby powiedzieć ,,symulacyjnym”) odpowiednikiem gęstości: spośród wylosowanych wyników zliczane są punkty należące do poszczególnych przedziałów.

Rozkład normalny 2-wymiarowy i rozkłady brzegowe

Rys. 3.1. Dwuwymiarowy rozkład normalny i rozkłady brzegowe.

Przykład 3.5 (Rozkład Poissona)

Algorytm przedstawiony niżej nie jest efektywny, ale jest prosty do zrozumienia.

$c:={\rm e}^{{-\lambda}}$

Gen $U$ ; $P:=U$ ; $N:=0$

while $P\geq c$ do

begin Gen $U$ ; $P:=PU$ ; $N:=N+1$ end

Na wyjściu $N\sim{\rm Poiss}({\lambda})$ . Istotnie, niech $E_{1},\ldots,E_{n},\ldots$ będą i.i.d. $\sim{\rm Ex}(1)$ i $S_{n}=E_{1}+\cdots+E_{n}$ . Wykorzystamy znany fakt, że $N=\max\{ n:S_{n}\leq\lambda\}$ ma rozkład ${\rm Poiss}(\lambda)$ . Zmienne o rozkładzie wykładniczym przedstawiamy jako $E_{i}=-\ln U_{i}$ – patrz Przykład 3.2. Zamiast dodawać zmienne $E_{i}$ możemy mnożyć zmienne $U_{i}$ . Mamy $N=\max\{ n:P_{n}\geq{\rm e}^{{-\lambda}}\}$ , gdzie $P_{n}=U_{1}\cdots U_{n}$ .

3.2. Metoda przekształceń

Zmienna losowa $Y$ , która ma postać $Y=h(X)$ , a więc jest pewną funkcją zmiennej $X$ , w naturalny sposób ,,dziedziczy” rozkład prawdopodobieństwa zgodnie z ogólnym schematem $\mathbb{P}(Y\in\cdot)=\mathbb{P}(h(X)\in\cdot)=\mathbb{P}(X\in h^{{-1}}(\cdot))$ (,,wykropkowany” argument jest zbiorem). Przy tym zmienne $X$ i $Y$ nie muszą być jednowymiarowe. Jeśli obie zmienne mają ten sam wymiar i przekształcenie $h$ jest dyfeomorfizmem, to dobrze znany wzór wyraża gęstość rozkładu $Y$ przez gęstość $X$ (Twierdzenie 5.1). Odpowiednio dobierając funkcję $h$ możemy ,,przetwarzać” jedne rozkłady prawdopodobieństwa na inne, nowe.

Prawie wszystkie algorytmy generowania zmiennych losowych zawierają przekształcenia zmiennych losowych jako część składową. W niemal ,,czystej” postaci metoda przekształceń pojawiła się w algorytmie Boxa-Müllera, Przykładzie 3.4. Najważniejszym być może szczególnym przypadkiem metody przekształceń jest odwracanie dystrybuanty.

3.2.1. Odwrócenie dystrybuanty

Faktycznie, ta metoda została już wykorzystana w Przykładzie 3.2. Opiera się ona na prostym fakcie. Jeżeli $F$ jest ciągłą i ściśle rosnącą dystrybuantą, $U\sim{\rm U}(0,1)$ i $X=F^{{-1}}(U)$ , to $X=F^{{-1}}(U)\sim F$ . Następująca definicja funkcji ,,pseudo-odwrotnej” pozwala pozbyć się kłopotliwych założeń.

Definicja 3.1

Jeżeli $F:\mathbb{R}\to[0,1]$ jest dowolną dystrybuantą, to funkcję $F^{-}:]0,1[\to\mathbb{R}$ określamy wzorem:

$F^{-}(u)=\inf\{ x:F(x)\geq u\}.$

Stwierdzenie 3.1

Nierówność $F^{-}(u)\leq x$ jest równoważna $u\leq F(x)$ , dla dowolnych $u\in]0,1[$ i $x\in\mathbb{R}$ .

Dowód

Z prawostronnej ciągłości dystrybuanty $F$ wynika, że kres dolny w Definicji 3.1 jest osiągany, czyli

$F(F^{-}(u))\geq u.$

Z drugiej strony,

$F^{-}(F(x))=\min\{ y:F(y\geq F(x)\}\leq x,$

po prostu dlatego, że $x\in\{ y:F(y\geq F(x)\}$ . Teza stwierdzenia natychmiast wynika z dwóch nierówności powyżej.

∎

Wniosek 3.1 (Ogólna metoda odwrócenia dystrybuanty)

Jeżeli $U\sim{\rm U}(0,1)$ i $X=F^{-}(U)$ , to $\mathbb{P}(X\leq x)=F(x)$ . W skrócie, $X\sim F$ .

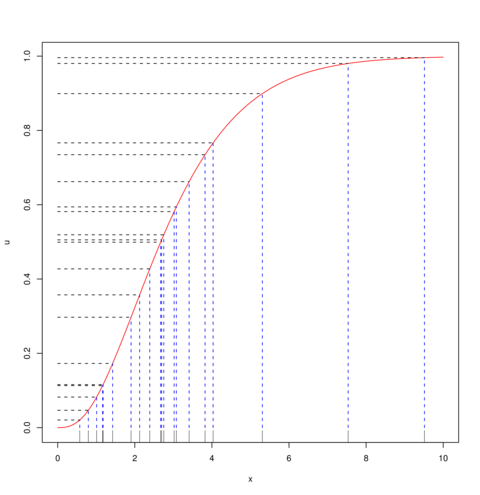
$Zmienne losowe $U_{i}$ o rozkładzie jednostajnym i wartości $F^{{-}}(U_{i})$$

Rys. 3.2. Odwracanie dystrybuanty.

Na Rysunku 3.2 widać 20 punktów $U_{1},\ldots,U_{{20}}$ , które wylosowałem z rozkładu ${\rm U}(0,1)$ (na osi pionowej) i odpowiadające im punkty $X_{i}=F^{{-1}}(U_{i})$ (na osi poziomej). W tym przypadku, $F$ jest dystrybuantą rozkładu ${\rm Gamma}(3,1)$ (linia krzywa). Najważniejszy fragment kodu w R jest taki:

curve(pgamma(x,shape=3,rate=1), from=0,to=10) # rysowanie F
U <- runif(20);X <- qgamma(U,shape=3,rate=1)

Zauważmy, że ta metoda działa również dla rozkładów dyskretnych i sprowadza się wtedy do metody ,,oczywistej”.

Przykład 3.6 (Rozkłady dyskretne)

Załóżmy, że $\mathbb{P}(X=i)=p_{i}$ dla $i=1,2,\ldots$ i $\sum p_{i}=1$ . Niech $s_{0}=0$ , $s_{k}=\sum _{{i=1}}^{k}p_{i}$ . Jeżeli $F$ jest dystrybuantą zmiennej losowej $X$ , to

$F^{-}(u)=i\quad\text{wtedy i tylko wtedy gdy}\quad s_{{i-1}}<u\leq s_{{i}}.$

Odwracanie dystrybuanty ma ogromne znaczenie teoretyczne, bo jest całkowicie ogólną metodą generowania dowolnych zmiennych losowych jednowymiarowych. Może się to wydać dziwne, ale w praktyce ta metoda jest używana stosunkowo rzadko, z dwóch wzgłędów:

Obliczanie 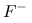$F^{-}$ j bywa trudne i nieefektywne.
Stosowalność metody ogranicza się do zmiennych losowych jednowymiarowych.

Podam dwa przykłady, w których zastosowanie metody odwracanie dystrybuanty jest rozsądne

Przykład 3.7 (Rozkład Weibulla)

Z definicji, $X\sim{\rm Weibull}(\beta)$ , jeśli

$F(x)=1-\exp(-x^{{\beta}})$

dla $x\geq 0$ . Odwrócenie dystrybuanty i generacja $X$ są łatwe:

$X=(-\ln U)^{{{1}/{\beta}}},\quad U\sim{\rm U}(0,1).$

Przykład 3.8 (Rozkład Cauchy'ego)

Gęstość i dystrybuanta zmiennej $X\sim{\rm Cauchy}(0,1)$ są następujące:

$f(x)=\frac{1}{\pi}\frac{1}{1+x^{2}},\qquad F(x)=\frac{1}{2}+\frac{1}{\pi}\arctan(x).$

Można tę zmienną generować korzystająć z wzoru:

$X=\tan\left(\pi\left(U-\frac{1}{2}\right)\right),\quad U\sim{\rm U}(0,1).$

3.3. Metoda eliminacji

To jest najważniejsza, najczęściej stosowana i najbardziej uniwersalna metoda. Zacznę od raczej oczywistego faktu, który jest w istocie probabilistycznym sformułowaniem definicji prawdopodobieństwa warunkowego.

Stwierdzenie 3.2

Przypuśćmy, że $Z=Z_{1},\ldots,Z_{n},\ldots$ jest ciągiem niezależnych zmiennych losowych o jednakowym rozkładzie, o wartościach w przestrzeni ${\cal Z}$ . Niech $C\subseteq{\cal Z}$ będzie takim zbiorem, że $\mathbb{P}(Z\in A)>0$ . Niech

$N=\min\{ n:Z_{n}\in C\}.$

Zmienne losowe $N$ i $Z_{N}$ są niezależne, przy tym

$\mathbb{P}(Z_{N}\in B)=\mathbb{P}(Z\in B|Z\in C)\quad\text{dla dowolnego}\quad B\subseteq{\cal Z},$

zaś

$\mathbb{P}(N=n)=pq^{{n-1}},\quad(n=1,2,\ldots),\quad\text{gdzie}\quad p=\mathbb{P}(Z\in C).$

Dowód

Wystarczy zauważyć, że

$\begin{split}\mathbb{P}(X_{N}\in B,N=n)&=\mathbb{P}(Z_{1}\not\in C,\ldots,Z_{{n-1}}\not\in C,Z_{n}\in C\cap B)\\ &=\mathbb{P}(Z_{1}\not\in C)\cdots\mathbb{P}(Z_{{n-1}}\not\in C)\mathbb{P}(Z_{n}\in C\cap B)\\ &=q^{{n-1}}\mathbb{P}(Z\in C\cap B)=q^{{n-1}}\mathbb{P}(Z\in B|Z\in C)p.\end{split}$

∎

W tym Stwierdzeniu ${\cal Z}$ może być dowolną przestrzenią mierzalną, zaś $C$ i $B$ – dowolnymi zbiorami mierzalnymi. Stwierdzenie mówi po prostu, że prawdopodobieństwo warunkowe odpowiada doświadczeniu losowemu powtarzanemu aż do momentu spełnienia warunku, przy czym rezultaty poprzednich doświadczeń się ignoruje (stąd nazwa: eliminacja).

3.3.1. Ogólny algorytm

Zakładamy, że umiemy generować zmienne losowe o gęstości $g$ , a chcielibyśmy otrzymać zmienną o gęstości proporcjonalnej do funkcji $f$ . Zakładamy, że $0\leq f\leq g$ .

repeat

Gen $Y\sim g$ ;

Gen $U\sim{\rm U}(0,1)$

until $U\leq\displaystyle\frac{f(Y)}{g(Y)}$ ;

$X:=Y$

Dowód poprawności algorytmu

Na mocy Stwierdzenia 3.2, zastosowanego do zmiennych losowych $Z=(Y,U)$ wystarczy pokazać, że

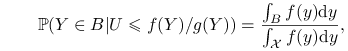$\qquad\mathbb{P}(Y\in B|U\leq f(Y)/g(Y))=\frac{\int _{B}f(y){\rm d}y}{\int _{{\cal X}}f(y){\rm d}y},$

(3.1)

gdzie ${\cal X}$ jest przestrzenią wartości zmiennej losowej $Y$ (i docelowej zmiennej losowej $X$ ). Warunkujemy teraz przez wartości zmiennej $Y$ , otrzymując

$\begin{split}\mathbb{P}(Y\in B,U\leq f(Y)/g(Y))&\int _{B}\mathbb{P}(U\leq f(Y)/g(Y)|Y=y)g(y){\rm d}y\\ &\int _{B}\frac{f(y)}{g(y)}g(y){\rm d}y=\int _{B}f(y){\rm d}y.\end{split}$

Skorzystaliśmy z niezależności $Y$ i $U$ oraz ze wzoru na prawdopodobieństwo całkowite. Otrzymaliśmy licznik we wzorze (3.1). Mianownik dostaniemy zastępując $B$ przez ${\cal X}$ .

∎

Uwaga 3.1

Ważną zaletą algorytmu jest to, że nie trzeba znać ,,stałej normującej” gęstości $f/\int f$ , czyli liczby $\int f$ .

Uwaga 3.2

W istocie ${\cal X}$ może być ogólną przestrzenią z miarą $\mu$ . Żeby poczuć się pewniej założę, że ${\cal X}$ jest przestrzenią polską i miara $\mu$ jest $\sigma$ -skończona. Możemy rozważać gęstości i całki względem miary $\mu$ – dowód poprawości algorytmu eliminacji nie ulega zmianie. Nie widzę wielkiego sensu w przeładowaniu notacji, można się umówić, że symbol $\int\cdots{\rm d}x$ jest skrótem $\int\cdots\mu({\rm d}x)$ . Dociekliwy Czytelnik powinien zastanowić się, w jakiej sytuacji potrafi uzasadnić wszystkie przejścia w dowodzie, powołując się na odpowiednie własności prawdopodobieństwa warunkowego (np. twierdzenie o prawdopodobieństwie całkowitym itp.). W każdym razie, algorytm eliminacji działa poprawnie, gdy

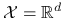${\cal X}=\mathbb{R}^{d}$ , gęstości są względem miary Lebesgue'a;
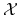${\cal X}$ dyskretna, gęstości są względem miary liczącej.

Uwaga 3.3

Efektywność algorytmu zależy od dobrania gęstości $g$ tak, aby majoryzowała funkcję $f$ ale nie była dużo od niej większa. Istotnie, liczba prób $N$ do zaakceptowania $X:=Y$ ma rozkład geometryczny z prawdopodobieństwem sukcesu $p=\int f/\int g$ , zgodnie ze Stwierdzeniem 3.2, zatem $\mathbb{E}N=1/p$ . Iloraz $p$ powinien być możliwie bliski jedynki, co jest możliwe jeśli ,,kształt funkcji $g$ jest podobny do $f$ .

Zwykle metoda eliminacji stosuje się w połączeniu z odpowiednio dobranymi przekształceniami. Zilustrujmy to na poniższym przykładzie.

Przykład 3.9 (Rozkład Beta, algorytm Bermana)

Niech $U$ i $V$ będą niezależnymi zmiennymi losowymi o rozkładzie jednostajnym ${\rm U}(0,1)$ . Pod warunkiem, że $U^{{1/\alpha}}+V^{{1/\beta}}$ zmienna losowa $U$ ma gęstość $f_{U}(u)$ proporcjonalną do funkcji $(1-u^{{1/\alpha}})^{\beta}$ . Zmienna losowa $X=U^{{1/\alpha}}$ ma gęstość $f_{X}(x)=f_{U}(x^{\alpha})({\rm d}x^{\alpha}/{\rm d}x)\propto(1-x)^{\beta}x^{\alpha}$ . Zatem $X$ ma rozkład ${\rm Beta}(\alpha,\beta+1)$ . Algorytm jest więc następujący:

repeat

Gen $U,V$

$X:=U^{{1/\alpha}}$ ; $Y:=V^{{1/\beta}}$

until $X+Y\leq 1$ ;

return $X$

Efektywność tego algorytmu jest tym większa, im mniejsze są parametry $\alpha$ i $\beta$ (frakcja zakceptowanych $U$ jest wtedy duża). Dla ilustracji rozpatrzmy dwa przypadki.

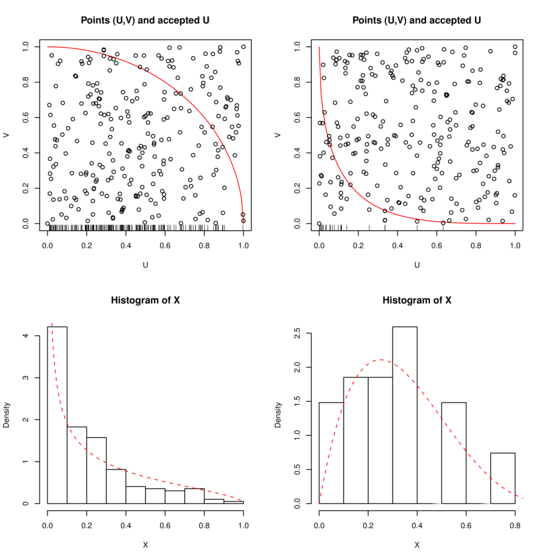
Algorytm Bermana: losowanie metodą eliminacji z rozkładu beta

Rys. 3.3. Algorytm Bermana: losowanie z rozkładu beta.

Na rysunku 3.3, po lewej stronie $\alpha=\beta=0.5$ . Spośród $n=250$ punktów zaakceptowano $N=197$ . Przerywana krzywa jest wykresem gęstości rozkładu ${\rm Beta}(0.5,1,5)$ . Po prawej stronie $\alpha=2$ , $\beta=3$ . Spośród $n=250$ punktów zaakceptowano tylko $N=24$ . Tym razem wykres pokazuje gęstość rozkładu ${\rm Beta}(2,4)$ . Zaakceptowane punkty $U$ (o gęstości $f_{U}$ ) są widoczne w postaci ,,kreseczek” na górnych rysunkach. Ciągłą linią jest narysowana funkcja $(1-u^{{1/\alpha}})^{\beta}\propto f_{U}(u)$ .

3.3.2. Eliminacja w R

Zasadniczy algorytm eliminacji opisany w Stwierdzeniu 3.2 i w Punkcie 3.3.1 polega na powtarzaniu generacji tak długo, aż zostanie spełnione kryterium akceptacji. Liczba prób jest losowa, a rezultatem jest jedna zmienna losowa o zadanym rozkładzie. Specyfika języka R narzuca inny sposób przeprowadzania eliminacji. Działamy na wektorach, a więc od razu produkujemy $n$ niezależnych zmiennych $X_{1},\ldots,X_{n}$ o rozkładzie $g$ , następnie poddajemy je wszystkie procedurze eliminacji. Przez sito eliminacji, powiedzmy $U_{i}<f(X_{i})/g(X_{i})$ , przechodzi pewna część zmiennych. Otrzymujemy losową liczbę zmiennych o rozkładzie proporcjonalnym do $f$ . Liczba zaakceptowanych zmiennych ma oczywiście rozkład dwumianowy ${\rm Bin}(n,p)$ z $p=\int f/\int g$ . To nie jest zbyt eleganckie. W sztuczny sposób można zmusić R do wyprodukowania zadanej, nielosowej liczby zaakceptowanych zmiennych, ale jeśli nie ma specjalnej konieczności, lepiej tego nie robić (przymus rzadko prowadzi do pozytywnych rezultatów).

Dla przykładu, generowanie zmiennych $(X,Y)$ o rozkładzie jesnostajnym na kole $\{ x^{2}+y^{2}\leq 1\}$ może w praktyce wyglądać tak:

> n <- 1000
> X <- runif(n,min=-1,max=1)  \# generowanie z rozkładu jednostajnego na [-1,1]
> Y <- runif(n,min=-1,max=1)
> Accept <- X^2+Y^2<1    \# wektor logiczny
> X <- X[Accept]
> Y <- Y[Accept]

Otrzymujemy pewną losową liczbę (około 785) punktów $(X,Y)$ w kole jednostkowym.

3.4. Metoda kompozycji

Jest to niezwykle prosta technika generowania zmiennych losowych. Załóżmy, że docelowy rozkład jest mieszanką prostszych rozkładów prawdopodobieństwa, czyli jego gęstość jest kombinacją wypukłą postaci

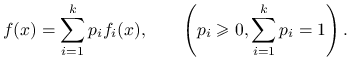$f(x)=\sum _{{i=1}}^{k}p_{i}f_{i}(x),\qquad\left(p_{i}\geq 0,\sum _{{i=1}}^{k}p_{i}=1\right).$