Zagadnienia
6. Symulowanie procesów stochastycznych I.
Pełny tytuł tego rozdziału powinien brzmieć ,,Symulacje Niektórych Procesów Stochastycznych, Bardzo Subiektywnie Wybranych Spośród Mnóstwa Innych”. Nie będę szczegółowo tłumaczył, skąd pochodzi mój subiektywny wybór. Zrezygnowałem z próby przedstawienia procesów z czasem ciągłym i równocześnie ciągłą przestrzenią stanów, bo to temat oddzielny i obszerny.
6.1. Stacjonarne procesy Gaussowskie
Ograniczymy się do dwóch klas procesów, często używanych do modelowania różnych zjawisk.
Będą to procesy z czasem dyskretnym i przestrzenią stanów ![]() , to znaczy ciągi
(zależnych) zmiennych losowych
, to znaczy ciągi
(zależnych) zmiennych losowych ![]() o wartościach rzeczywistych.
Niech
o wartościach rzeczywistych.
Niech ![]() będzie ciągiem niezależnych zmiennych losowych o jednakowym rozkładzie
będzie ciągiem niezależnych zmiennych losowych o jednakowym rozkładzie ![]() (wygodnie posłużyć się tutaj
ciągiem indeksowanym wszystkimi liczbami całkowitymi).
(wygodnie posłużyć się tutaj
ciągiem indeksowanym wszystkimi liczbami całkowitymi).
Definicja 6.1
Proces ruchomych średnich rzędu ![]() , w skrócie MA
, w skrócie MA![]() jest określony
równaniem
jest określony
równaniem
gdzie ![]() jest ustalonym ciągiem współczynników.
jest ustalonym ciągiem współczynników.
Sposób generowania takiego procesu jest oczywisty i wynika wprost z definicji.
Co więcej widać, że proces MA![]() jest stacjonarny, to znaczy łączny rozkład prawdopodobieństwa
zmiennych
jest stacjonarny, to znaczy łączny rozkład prawdopodobieństwa
zmiennych ![]() jest taki sam jak zmiennych
jest taki sam jak zmiennych ![]() , dla dowolnych
, dla dowolnych ![]() i
i ![]() . Intuicyjnie, proces nie zmienia się
po ,,przesunięciu czasu” o
. Intuicyjnie, proces nie zmienia się
po ,,przesunięciu czasu” o ![]() jednostek.
jednostek.
Definicja 6.2
Proces autoregresji rzędu ![]() , w skrócie AR
, w skrócie AR![]() jest określony
równaniem rekurencyjnym
jest określony
równaniem rekurencyjnym
gdzie ![]() jest ustalonym ciągiem współczynników.
jest ustalonym ciągiem współczynników.
Procesy autoregresji wydają się bardzo odpowiednie do modelowania ,,szeregów czasowych”:
stan układu w chwili ![]() zależy od stanów przeszłych i dotatkowo jeszcze od przypadku.
Procesy AR
zależy od stanów przeszłych i dotatkowo jeszcze od przypadku.
Procesy AR![]() , w szczególności są łańcuchami Markowa. Sposób generowania
procesów AR
, w szczególności są łańcuchami Markowa. Sposób generowania
procesów AR![]() jest też bezpośrednio widoczny z definicji. Pojawia się jednak pewien problem.
Jak znaleźć
jest też bezpośrednio widoczny z definicji. Pojawia się jednak pewien problem.
Jak znaleźć ![]() na początku algorytmu w taki sposób, żeby proces był
stacjonarny? Jest to o tyle istotne, że rzeczywiste procesy (na przykład czeregi czasowe
w zastosowaniach ekonomicznych) specjaliści uznają za stacjonarne, przynajmniej w przybliżeniu.
na początku algorytmu w taki sposób, żeby proces był
stacjonarny? Jest to o tyle istotne, że rzeczywiste procesy (na przykład czeregi czasowe
w zastosowaniach ekonomicznych) specjaliści uznają za stacjonarne, przynajmniej w przybliżeniu.
Rozważmy dla wygody oznaczeń podwójnie nieskończony proces
spełniający równanie autoregresji rzędu ![]() . Załóżmy, że ten proces jest stacjonarny i wektor
. Załóżmy, że ten proces jest stacjonarny i wektor ![]() rozkład normalny,
rozkład normalny,
![]() . Stacjonarność implikuje, że elementy macierzy
. Stacjonarność implikuje, że elementy macierzy ![]() muszą być postaci
muszą być postaci ![]() . Mamy przy tym
. Mamy przy tym ![]() , co może być traktowane jako wygodna konwencja (po to właśnie ,,rozszerzamy” proces w obie strony).
Zastosowanie równania definiującego autoregresję prowadzi do wniosku, że
, co może być traktowane jako wygodna konwencja (po to właśnie ,,rozszerzamy” proces w obie strony).
Zastosowanie równania definiującego autoregresję prowadzi do wniosku, że
Podobnie,
gdzie ![]() .
Otrzymujemy następujący układ równań na współczynniki autokorelacji
.
Otrzymujemy następujący układ równań na współczynniki autokorelacji ![]() :
:
![\qquad\left\{\begin{array}[]{ll}\rho _{1}=\alpha _{1}+\alpha _{2}\rho _{{1}}+\alpha _{3}\rho _{2}+\ldots+\alpha _{p}\rho _{{p-1}},\\
\rho _{2}=\alpha _{1}\rho _{1}+\alpha _{2}+\alpha _{3}\rho _{1}+\ldots+\alpha _{p}\rho _{{p-2}},\\
\dots,\\
\rho _{p}=\alpha _{1}\rho _{{p-1}}+\alpha _{2}\rho _{{p-2}}+\alpha _{3}\rho _{2}+\ldots+\alpha _{p},\\
\end{array}\right.](wyklady/sst/mi/mi713.png) |
(6.1) |
Można pokazać, że ten ten układ ma rozwiązanie, jeśli wielomian
charakterystyczny
![]() nie ma zer w kole
nie ma zer w kole ![]() .
Ponadto mamy równanie na wariancję stacjonarną:
.
Ponadto mamy równanie na wariancję stacjonarną:
| (6.2) |
Metoda generowania stacjonarnego procesu AR![]() ,
, ![]() jest następująca. Znajdujemy rozwiązanie układu równań (6.1), wariancję obliczamy
ze wzoru (6.2) i tworzymy macierz
jest następująca. Znajdujemy rozwiązanie układu równań (6.1), wariancję obliczamy
ze wzoru (6.2) i tworzymy macierz ![]() . Generujemy wektor losowy
. Generujemy wektor losowy ![]() i dalej generujemy
rekurencyjnie
i dalej generujemy
rekurencyjnie ![]() używając równania autoregresji.
Aby się przekonać, że tak generowany proces jest stacjonarny, wystarczy sprawdzić że
identyczne są rozkłady wektorów
używając równania autoregresji.
Aby się przekonać, że tak generowany proces jest stacjonarny, wystarczy sprawdzić że
identyczne są rozkłady wektorów ![]() i
i ![]() .
Mamy
.
Mamy
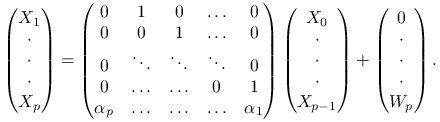 |
Niech ![]() oznacza ,,dużą macierz” w tym wzorze .
Z własności wielowymiarowych rozkładów normalnych wynika, że wystarczy sprawdzić równość
oznacza ,,dużą macierz” w tym wzorze .
Z własności wielowymiarowych rozkładów normalnych wynika, że wystarczy sprawdzić równość
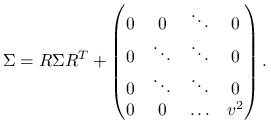 |
Macierz ![]() została tak wybrana, że ta równość jest spełniona.
została tak wybrana, że ta równość jest spełniona.
6.2. Procesy Poissona
6.2.1. Jednorodny proces Poissona na półprostej
Definicja 6.3
Rozważmy niezależne zmienne losowe ![]() o jednakowym rozkładzie wykładniczym,
o jednakowym rozkładzie wykładniczym, ![]() i
utwórzmy kolejne sumy
i
utwórzmy kolejne sumy
Niech, dla ![]() ,
,
Rodzinę zmiennych losowych ![]() nazywamy procesem Poissona.
nazywamy procesem Poissona.
Proces Poissona dobrze jest wyobrażać sobie jako losowy zbiór punktów
na półprostej: ![]() . Zmienna
. Zmienna ![]() oznacza liczbę punktów, które ,,wpadły” w odcinek
oznacza liczbę punktów, które ,,wpadły” w odcinek ![]() . Wygodnie będzie
używać symbolu
. Wygodnie będzie
używać symbolu
dla oznaczenia liczby punktów, które ,,wpadły” w odcinek ![]() .
.
Stwierdzenie 6.1
Jeśli ![]() jest procesem Poissona, to
jest procesem Poissona, to
Dowód
Zauważmy, że
Wobec tego ze wzoru na prawdopodobieństwo całkowite wynika, że
Oczywiście ![]() . Liczba
. Liczba
jest nazywana intensywnością procesu.
Stwierdzenie 6.2
Jeśli
to zmienne losowe ![]() są niezależne i każda
z nich ma rozkład Poissona:
są niezależne i każda
z nich ma rozkład Poissona:
Dowód
Pokażemy, że warunkowo, dla ![]() , ciąg zmiennych losowych
, ciąg zmiennych losowych
Wynika to z własności braku pamięci rozkładu wykładniczego.
W istocie, dla ustalonych ![]() i
i ![]() mamy
mamy
Fakt, że zmienne ![]() są niezależne od zdarzenia
są niezależne od zdarzenia
![]() jest oczywisty.
Pokazaliśmy w ten sposób, że losowy zbiór punktów
jest oczywisty.
Pokazaliśmy w ten sposób, że losowy zbiór punktów
![]() ma (warunkowo, dla
ma (warunkowo, dla
![]() ) taki sam rozkład prawdopodobieństwa, jak
) taki sam rozkład prawdopodobieństwa, jak
![]() . Proces Poissona obserwowany od
momentu
. Proces Poissona obserwowany od
momentu ![]() jest kopią wyjściowego procesu. Wynika stąd w szczególności,
że zmienna losowa
jest kopią wyjściowego procesu. Wynika stąd w szczególności,
że zmienna losowa ![]() jest niezależna od
jest niezależna od ![]() i
i ![]() . Dalsza część dowodu przebiega
analogicznie i ją pominiemy.
. Dalsza część dowodu przebiega
analogicznie i ją pominiemy.
Metoda generowania procesu Poisson oparta na Definicji 6.3 jest raczej oczywista. Zauważmy jednak, że nie jest to jedyna metoda. Inny sposób generowania (i inny sposób patrzenia na proces Poissona) jest związany z następującym faktem.
Stwierdzenie 6.3
Warunkowo, dla ![]() , ciąg zmiennych losowych
, ciąg zmiennych losowych
ma rozkład taki sam, jak ciąg statystyk pozycyjnych
z rozkładu ![]() .
.
Dowód
Z Wniosku 5.1 wynika, że warunkowo, dla ![]() ,
,
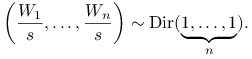 |
Innymi słowy wektor losowy ![]() ma taki rozkład, jak
ma taki rozkład, jak
![]() statystyk pozycyjnych z
statystyk pozycyjnych z ![]() .
.
Obliczmy warunkową gęstość zmiennej losowej ![]() , jeśli
, jeśli ![]() :
:
A zatem warunkowo, dla ![]() , zmienna losowa
, zmienna losowa ![]() ma rozklad
ma rozklad ![]() i w konsekwencji (przypomnijmy sobie algorytm generowania zmiennych o rozkładzie Dirichleta)
i w konsekwencji (przypomnijmy sobie algorytm generowania zmiennych o rozkładzie Dirichleta)
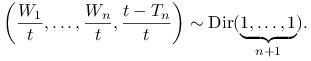 |
Innymi słowy wektor losowy ![]() ma taki rozkład, jak
ma taki rozkład, jak
![]() statystyk pozycyjnych z
statystyk pozycyjnych z ![]() .
.
Wynika stąd następujący sposób generowania procesu Poissona na przedziale
![]() .
.
| Gen |
| for |
| Sort |
Co ważniejsze, Stwierdzenia 6.1, 6.2 i 6.3 wskazują, jak powinny wyglądać uogólnienia procesu Poissona i jak generować takie ogólniejsze procesy. Zanim tym się zajmiemy, zróbmy dygresję i podajmy twierdzenie charakteryzujące ,,zwykły” proces Poissona. Nie jest ono bezpośrednio używane w symulacjach, ale wprowadza pewien ważny sposób określania procesów, który ułatwia zrozumienie łańcuchów Markowa z czasem ciągłym i jest bardzo użyteczny w probabilistycznym modelowaniu zjawisk.
Twierdzenie 6.1
Załóżmy, że ![]() jest procesem o wartościach w
jest procesem o wartościach w ![]() , stacjonarnych i niezależnych przyrostach (to znaczy
, stacjonarnych i niezależnych przyrostach (to znaczy ![]() jest niezależne od
jest niezależne od ![]() i ma rozkład zależny tylko od
i ma rozkład zależny tylko od ![]() dla dowolnych
dla dowolnych ![]() ) oraz, że
trajektorie
) oraz, że
trajektorie ![]() są prawostronnie ciągłymi funkcjami mającymi lewostronne granice (prawie na pewno).
Jeżeli
są prawostronnie ciągłymi funkcjami mającymi lewostronne granice (prawie na pewno).
Jeżeli ![]() i spełnione są następujące warunki:
i spełnione są następujące warunki:
to ![]() jest jednorodnym procesem Poissona z intensywnością
jest jednorodnym procesem Poissona z intensywnością ![]()
Bardzo prosto można zauważyć, że proces Poissona ![]() o intensywności
o intensywności ![]() ma własności wymienione w Twierdzeniu 6.1. Ciekawe jest, że te własności w pełni charakteryzują proces Poissona.
ma własności wymienione w Twierdzeniu 6.1. Ciekawe jest, że te własności w pełni charakteryzują proces Poissona.
Dowód Tw. 6.1 – szkic
Pokażemy tylko, że
Najpierw zajmiemy się funkcją ![]() .
Z niezależności i jednorodności przyrostów wynika tożsamość
.
Z niezależności i jednorodności przyrostów wynika tożsamość
Stąd
Przejdźmy do granicy z ![]() i skorzystajmy z własności (i) i (ii). Dostajemy proste
równanie różniczkowe:
i skorzystajmy z własności (i) i (ii). Dostajemy proste
równanie różniczkowe:
Rozwiązanie tego równania z warunkiem początkowym ![]() jest funkcja
jest funkcja
Bardzo podobnie obliczamy kolejne funkcje ![]() . Postępujemy rekurencyjnie: zakładamy, że
znamy
. Postępujemy rekurencyjnie: zakładamy, że
znamy ![]() i układamy równanie różniczkowe dla funkcji
i układamy równanie różniczkowe dla funkcji ![]() . Podobnie jak poprzednio,
. Podobnie jak poprzednio,
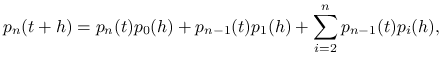 |
a zatem
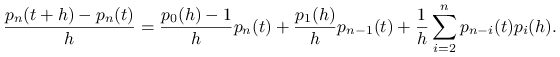 |
Korzystając z własności (i) i (ii) otrzymujemy równanie
To równanie można rozwiązać metodą uzmiennienia stałej: poszukujemy rozwiązania postaci
![]() . Zakładamy przy tym indukcyjnie, że
. Zakładamy przy tym indukcyjnie, że
![]() i mamy oczywisty warunek początkowy
i mamy oczywisty warunek początkowy
![]() . Stąd już łatwo dostać dowodzony wzór na
. Stąd już łatwo dostać dowodzony wzór na ![]() .
.
Na koniec zauważmy, że z postaci funkcji ![]() łatwo wywnioskować
jaki ma rozkład zmienna
łatwo wywnioskować
jaki ma rozkład zmienna ![]() . Istotnie,
. Istotnie, ![]()
![]() .
.
Własności (i) i (ii), w połączeniu z jednorodnością przyrostów można przepisać w następującej sugestywnej formie:
| (6.3) |
Jest to o tyle ważne, że w podobnym języku łatwo formułować założenia o ogólniejszych procesach, na przykład tak zwanych procesach urodzin i śmierci. Wrócimy do tego przy okazji omawiania łańcuchów Markowa.
6.2.2. Niejednorodne procesy Poissona w przestrzeni
Naturalne uogólnienia procesu Poissona polegają na tym, że
rozważa się losowe zbiory punktów w przestrzeni o dowolnym wymiarze i
dopuszcza się różną intensywność pojawiania się punktów w różnych rejonach
przestrzeni. Niech ![]() będzie przestrzenią polską. Czytelnik, który nie
lubi abstrakcji może założyć, że
będzie przestrzenią polską. Czytelnik, który nie
lubi abstrakcji może założyć, że ![]() .
.
Musimy najpierw wprowadzić odpowiednie oznaczenia. Rozważmy ciąg wektorów
losowych w ![]() :
:
(może to być ciag skonczony lub nie, liczba tych wektorów może być
zmienną losową). Niech, dla ![]() ,
,
oznacza liczbę wektorów, które ,,wpadły do zbioru ![]() ” (przy tym dopuszczamy wartość
” (przy tym dopuszczamy wartość ![]() i umawiamy się liczyć powtarzające się wektory tyle razy, ile razy występują w ciągu).
i umawiamy się liczyć powtarzające się wektory tyle razy, ile razy występują w ciągu).
Niech teraz ![]() będzie miarą na (
będzie miarą na (![]() -ciele borelowskich podzbiorów)
przestrzeni
-ciele borelowskich podzbiorów)
przestrzeni ![]() .
.
Definicja 6.4
![]() jest procesem Poissona z miara intensywnosci
jest procesem Poissona z miara intensywnosci ![]() , jesli
, jesli
-
dla parami rozłącznych zbiorów
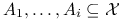 ,
odpowiadające im zmienne losowe
,
odpowiadające im zmienne losowe  są niezależne;
są niezależne; -
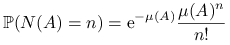 , dla
każdego
, dla
każdego 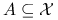 takiego, że
takiego, że 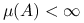 i dla
i dla 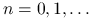 .
.
Z elementarnych własności rozkładu Poissona wynika następujący wniosek.
Wniosek 6.1
Rozważymy rozbicie zbioru ![]() o skończonej mierze intensywności,
o skończonej mierze intensywności, ![]() , na rozłączną sumę
, na rozłączną sumę ![]() . Wtedy
. Wtedy
Jeśli natomiast ![]() to łatwo zauważyć, że
to łatwo zauważyć, że ![]() z prawdopodobieństwem 1.
z prawdopodobieństwem 1.
Z Definicji 6.4 i Wniosku 6.1 natychmiast wynika następujący algorytm generowania procesu Poissona. Załóżmy, że interesuje nas ,,fragment” procesu w zbiorze ![]() o skończonej mierze intensywności. W praktyce zawsze symulacje muszą się
do takiego fragmentu ograniczać. Zauważmy, że unormowana miara
o skończonej mierze intensywności. W praktyce zawsze symulacje muszą się
do takiego fragmentu ograniczać. Zauważmy, że unormowana miara ![]() jest rozkładem prawdopodobieństwa (zmienna losowa
jest rozkładem prawdopodobieństwa (zmienna losowa ![]() ma
ten rozkład, jeśli
ma
ten rozkład, jeśli ![]() , dla
, dla ![]() ).
).
| Gen |
| for |
Należy rozumieć, że formalnie definiujemy ![]() dla
dla ![]() , w istocie jednak za realizację procesu uważamy zbiór punktów
, w istocie jednak za realizację procesu uważamy zbiór punktów ![]() (,,zapominamy” o uporządkowaniu punktów). Widać, że to jest proste uogólnienie analogicznego
algorytmu dla ,,zwykłego” procesu Poissona, podanego wcześniej.
(,,zapominamy” o uporządkowaniu punktów). Widać, że to jest proste uogólnienie analogicznego
algorytmu dla ,,zwykłego” procesu Poissona, podanego wcześniej.
Można również rozbić zbiór ![]() na rozłączną sumę
na rozłączną sumę ![]() i generować
niezależnie fragmenty procesu w każdej części
i generować
niezależnie fragmenty procesu w każdej części ![]() .
.
Przykład 6.1
Jednorodny proces Poissona na kole ![]() można wygenerować w następujący sposób. Powiedzmy, że intensywność (punktów na jednostkę pola) jest
można wygenerować w następujący sposób. Powiedzmy, że intensywność (punktów na jednostkę pola) jest ![]() , to znaczy
, to znaczy
![]() , gdzie
, gdzie ![]() jest polem (miarą Lebesgue'a) zbioru
jest polem (miarą Lebesgue'a) zbioru ![]() .
.
Najpierw generujemy ![]() , następnie punkty
, następnie punkty ![]() niezależnie z rozkładu
niezależnie z rozkładu ![]() . To wszystko.
. To wszystko.
Ciekawszy jest następny przykład.
Przykład 6.2 (Jednorodny proces Poissona w przestrzeni prostych)
Prostą na płaszczyźnie można sparametryzować
podając kąt ![]() jako tworzy prostopadła do prostej z osią poziomą oraz odległość
jako tworzy prostopadła do prostej z osią poziomą oraz odległość ![]() prostej od początku układu. Każda prosta jest więc opisana przez parę liczb
prostej od początku układu. Każda prosta jest więc opisana przez parę liczb
![]() czyli punkt przestrzeni
czyli punkt przestrzeni ![]() . Jeśli teraz
wygenerujemy jednorodny proces Poissona na tej przestrzeni, to znaczy proces o intensywności
. Jeśli teraz
wygenerujemy jednorodny proces Poissona na tej przestrzeni, to znaczy proces o intensywności
![]() ,
, ![]() , to można się spodziewać zbioru ,,losowo położonych
prostych”. To widać na Rysunku 6.1.
W istocie, wybór parametryzacji zapewnia, że rozkład prawdopodobieństwa procesu nie zależy
od wyboru układu współrzędnych. Dowód, czy nawet precyzyjne sformułowanie tego stwierdzenia przekracza ramy tego skryptu. Intuicyjnie chodzi o to, że na obrazku ,,nie ma wyróżnionego kierunku ani wyróżnionego punktu”.
Nie można sensownie zdefiniować pojęcia ,,losowej prostej” ale każdy przyzna, że proces Poissona o którym mowa można uznać za uściślenie intuicyjnie rozumianego pojęcia
,,losowego zbioru prostych”.
, to można się spodziewać zbioru ,,losowo położonych
prostych”. To widać na Rysunku 6.1.
W istocie, wybór parametryzacji zapewnia, że rozkład prawdopodobieństwa procesu nie zależy
od wyboru układu współrzędnych. Dowód, czy nawet precyzyjne sformułowanie tego stwierdzenia przekracza ramy tego skryptu. Intuicyjnie chodzi o to, że na obrazku ,,nie ma wyróżnionego kierunku ani wyróżnionego punktu”.
Nie można sensownie zdefiniować pojęcia ,,losowej prostej” ale każdy przyzna, że proces Poissona o którym mowa można uznać za uściślenie intuicyjnie rozumianego pojęcia
,,losowego zbioru prostych”.
Ciekawe, że podstawowe metody generowania zmiennych losowych mają swoje odpowiedniki dla procesów Poissona. Rolę rozkładu prawdopodobieństwa przejnuje miara intensywności.
Przykład 6.3 (Odwracanie dystrybuanty)
Dla miary intensywności ![]() na przestrzeni jednowymiarowej można zdefiniować dystrybuantę tej miary.
Dla uproszczenia rozważmy przestrzeń
na przestrzeni jednowymiarowej można zdefiniować dystrybuantę tej miary.
Dla uproszczenia rozważmy przestrzeń ![]() i założymy, że każdy zbiór ograniczony ma
miarę skończoną.
Niech
i założymy, że każdy zbiór ograniczony ma
miarę skończoną.
Niech ![]() . Funkcję
. Funkcję ![]() nazwiemy dystrybuantą. Jest ona niemalejąca, prawostronnie ciągła, ale granica w nieskończoności
nazwiemy dystrybuantą. Jest ona niemalejąca, prawostronnie ciągła, ale granica w nieskończoności
![]() może być dowolnym elementem z
może być dowolnym elementem z ![]() .
Dla procesu Poissona na
.
Dla procesu Poissona na ![]() wygodnie wrócić do prostszych oznaczeń, pisząc
wygodnie wrócić do prostszych oznaczeń, pisząc ![]() jak we wcześniej rozpatrywanym przypadku jednorodnym.
jak we wcześniej rozpatrywanym przypadku jednorodnym.
Niech ![]() będzie jednorodnym procesem Poissona na
będzie jednorodnym procesem Poissona na ![]() z intensywnoscia równą 1.
Wtedy
z intensywnoscia równą 1.
Wtedy
jest niejednorodnym procesem Poissona z miarą intensywności ![]() . W istocie,
jeśli
. W istocie,
jeśli ![]() to
to ![]() są niezależne i maja
rozkłady odpowiednio
są niezależne i maja
rozkłady odpowiednio ![]() .
Zauważmy, że jeśli
.
Zauważmy, że jeśli ![]() oznaczają punkty skoku procesu
oznaczają punkty skoku procesu ![]() to
to
![]() ,
gdzie
,
gdzie ![]() jest uogólnioną funkcją odwrotną do dystrybuanty. Wobec tego
punktami skoku procesu
jest uogólnioną funkcją odwrotną do dystrybuanty. Wobec tego
punktami skoku procesu ![]() są
są ![]() . Algorytm jest taki:
. Algorytm jest taki:
| Gen |
| for |
Pominęliśmy tu sortowanie skoków i założyliśmy, że symulacje ograniczamy do odcinka ![]() .
.
Przykład 6.4 (Przerzedzanie)
To jest odpowiednik metody eliminacji. Załóżmy, że
mamy dwie miary intensywności: ![]() o gęstości
o gęstości ![]() i
i ![]() o gęstości
o gęstości ![]() .
To znaczy, że
.
To znaczy, że ![]() i
i ![]() dla dowolnego zbioru
dla dowolnego zbioru ![]() . Załóżmy, że
. Załóżmy, że ![]() i
przypuśćmy, że umiemy generować proces Poissona o intensywności
i
przypuśćmy, że umiemy generować proces Poissona o intensywności ![]() . Niech
. Niech
![]() będą punktami tego procesu w zborze
będą punktami tego procesu w zborze ![]() o skończonej mierze
o skończonej mierze ![]() (wiemy, że
(wiemy, że ![]() ). Punkt
). Punkt ![]() akceptujemy z prawdopodobieństwem
akceptujemy z prawdopodobieństwem
![]() (pozostawiamy w zbiorze) lub odrzucamy (usuwamy ze zbioru) z prawdopodobieństwem
(pozostawiamy w zbiorze) lub odrzucamy (usuwamy ze zbioru) z prawdopodobieństwem
![]() . Liczba pozostawionych punktów
. Liczba pozostawionych punktów ![]() ma rozkład
ma rozkład ![]() , zaś każdy z
tych punktów ma rozkład o gęstości
, zaś każdy z
tych punktów ma rozkład o gęstości ![]() , gdzie
, gdzie ![]() .
Te punkty tworzą proces Poissona z miarą intensywności
.
Te punkty tworzą proces Poissona z miarą intensywności ![]() .
.
| Gen |
| for |
| if |
| return |
Przykład 6.5 (Superpozycja)
To jest z kolei odpowiednik metody kompozycji.
Metoda opiera się na następującym prostym fakcie. Jezeli
![]() są niezależnymi procesami Poissona z miarami intensywnosci
odpowiednio
są niezależnymi procesami Poissona z miarami intensywnosci
odpowiednio ![]() , to
, to ![]() jest procesem Poissona z intensywnością
jest procesem Poissona z intensywnością ![]() . Dodawanie należy tu rozumieć w dosłaowny sposób, to znaczy
. Dodawanie należy tu rozumieć w dosłaowny sposób, to znaczy ![]() jest określone jako
jest określone jako ![]() dla każdego zbioru
dla każdego zbioru
![]() . Jeśli utożsamimy procesy z losowymi zbiorami punktów to odpowiada temu operacja brania sumy mnogościowej (złączenia zbiorów). Niech
. Jeśli utożsamimy procesy z losowymi zbiorami punktów to odpowiada temu operacja brania sumy mnogościowej (złączenia zbiorów). Niech
![]() będą punktami
będą punktami ![]() -tego procesu w zborze
-tego procesu w zborze ![]() o skończonej mierze
o skończonej mierze
![]() .
.
| for |
| begin |
| Gen |
| |
| end |
| return |
| { mamy tu |
Wygodnie jest utożsamiać procesy Poissona z losowymi zbiorami punktów, jak uczyniliśmy w ostatnich przykładach (i mniej jawnie w wielu miejscach wcześniej). Te zbiory można rozumieć w zwykłym sensie, dodawać, odejmować tak jak w teorii mnogości pod warunkiem, że ich elementy się nie powtarzają. W praktyce mamy najczęściej do czynienia z intensywnościami, które mają gęstości ,,w zwykłym sensie”, czyli względem miary Lebesgue'a. Wtedy, z prawdopodobieństwem 1, punkty procesu Poissona nie powtarzają się.