Zagadnienia
7. Symulowanie procesów stochastycznych II. Procesy Markowa
7.1. Czas dyskretny, przestrzeń dyskretna
Zacznijmy od najprostszej sytuacji.
Rozważmy skończony zbiór ![]() , który będziemy nazywali przestrzenią
stanów. Czasem wygodnie przyjąć, że
, który będziemy nazywali przestrzenią
stanów. Czasem wygodnie przyjąć, że ![]() . Jest to tylko
umowne ponumerowanie stanów.
. Jest to tylko
umowne ponumerowanie stanów.
Definicja 7.1
(i)
Ciąg ![]() zmiennych losowych o wartościach w
zmiennych losowych o wartościach w ![]() nazywamy łańcuchem Markowa, jeśli dla każdego
nazywamy łańcuchem Markowa, jeśli dla każdego
![]() i dla każdego ciągu
i dla każdego ciągu ![]() punktów
przestrzeni
punktów
przestrzeni ![]() ,
,
(o ile tylko ![]() , czyli
prawdopodobieństwo warunkowe w tym wzorze ma sens).
, czyli
prawdopodobieństwo warunkowe w tym wzorze ma sens).
(ii) Łańcuch Markowa nazywamy jednorodnym, jeśli dla dowolnych stanów ![]() i
i ![]() i każdego
i każdego ![]() możemy napisać
możemy napisać
to znaczy prawdopodobieństwo warunkowe w powyższym wzorze zależy tylko od ![]() i
i ![]() ,
ale nie zależy od
,
ale nie zależy od ![]() .
.
Jeśli ![]() , to
mówimy, że łańcuch w chwili
, to
mówimy, że łańcuch w chwili ![]() znajduje się w stanie
znajduje się w stanie ![]() .
Warunek (i) w Definicji 7.1 znaczy tyle, że przyszła ewolucja łańcucha zależy od stanu obecnego, ale nie zależy od przeszłości. Łańcuch jest jednorodny, jeśli prawo ewolucji łańcucha nie zmienia
się w czasie. W dalszym ciągu rozpatrywać będziemy głównie łańcuchy jednorodne. Macierz
.
Warunek (i) w Definicji 7.1 znaczy tyle, że przyszła ewolucja łańcucha zależy od stanu obecnego, ale nie zależy od przeszłości. Łańcuch jest jednorodny, jeśli prawo ewolucji łańcucha nie zmienia
się w czasie. W dalszym ciągu rozpatrywać będziemy głównie łańcuchy jednorodne. Macierz
![P=\left(P(x,y)\right)_{{x,y\in{\cal X}}}=\left(\begin{array}[]{ccccc}P(1,1)&\cdots&P(1,y)&\cdots&P(1,d)\cr\vdots&\ddots&\vdots&\ddots&\vdots\cr P(x,1)&\cdots&P(x,y)&\cdots&P(x,d)\cr\vdots&\ddots&\vdots&\ddots&\vdots\cr P(d,1)&\cdots&P(d,y)&\cdots&P(d,d)\cr\end{array}\right)](wyklady/sst/mi/mi813.png) |
nazywamy macierzą (prawdopodobieństw) przejścia łańcucha. Jest to macierz
stochastyczna, to znaczy ![]() dla dowolnych stanów
dla dowolnych stanów ![]() oraz
oraz
![]() dla każdego
dla każdego ![]() . Jeśli
. Jeśli ![]() , to wektor
wierszowy
, to wektor
wierszowy
nazywamy rozkładem początkowym łańcucha (oczywiście,
![]() ). Jest jasne, że
). Jest jasne, że
| (7.1) |
Ten wzór określa jednoznacznie łączny rozkład prawdopodobieństwa zmiennych
![]() i może być przyjęty za definicję
jednorodnego łańcucha Markowa. W tym sensie możemy utożsamić
łańcuch z parą
i może być przyjęty za definicję
jednorodnego łańcucha Markowa. W tym sensie możemy utożsamić
łańcuch z parą ![]() : łączny rozkład prawdopodobieństwa jest wyznaczony przez
podanie rozkładu początkowego i macierzy przejścia.
: łączny rozkład prawdopodobieństwa jest wyznaczony przez
podanie rozkładu początkowego i macierzy przejścia.
Opiszemy teraz bardzo ogólną konstrukcję, która jest podstawą algorytmów generujących łańcuchy Markowa. Wyobraźmy sobie, jak zwykle, że mamy do dyspozycji ciąg
![]() ,,liczb losowych”, produkowanych przez komputerowy generator,
czyli z teoretycznego punktu widzenia ciąg niezależnych zmiennych losowych o jednakowym rozkładzie,
,,liczb losowych”, produkowanych przez komputerowy generator,
czyli z teoretycznego punktu widzenia ciąg niezależnych zmiennych losowych o jednakowym rozkładzie, ![]() .
Niech
.
Niech ![]() i
i ![]() będą takimi funkcjami, że
będą takimi funkcjami, że
| (7.2) |
Jeśli określimy ![]() rekurencyjnie w następujący sposób:
rekurencyjnie w następujący sposób:
| (7.3) |
to jest jasne, że tak otrzymany ciąg zmiennych losowych jest łańcuchem Markowa
z rozkładem początkowym ![]() i macierzą przejścia
i macierzą przejścia ![]() .
.
Na zakończenie tego podrozdziału zróbmy kilka prostych uwag.
-
Wszystko, co w tym podrozdziale zostało powiedziane można niemal mechanicznie uogólnić na przypadek nieskończonej ale przeliczalnej przestrzeni
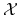 .
. -
Można sobie wyobrażać, że dla ustalonego
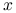 , zbiór
, zbiór 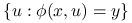 jest odcinkiem
długości
jest odcinkiem
długości 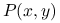 , ale nie musimy tego żądać.
Nie jest istotne, że zmienne
, ale nie musimy tego żądać.
Nie jest istotne, że zmienne 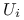 mają rozkład
mają rozkład 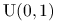 . Moglibyśmy założyć, że
są określone na dość dowolnej przestrzeni
. Moglibyśmy założyć, że
są określone na dość dowolnej przestrzeni 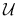 . Istotne jest, że te zmienne są niezależne,
mają jednakowy rozkład i zachodzi wzór (7.2). W praktyce bardzo często
do zrealizowania jednego ,,kroku” łańcucha Markowa generujemy więcej niż jedną ,,liczbę
losową”.
. Istotne jest, że te zmienne są niezależne,
mają jednakowy rozkład i zachodzi wzór (7.2). W praktyce bardzo często
do zrealizowania jednego ,,kroku” łańcucha Markowa generujemy więcej niż jedną ,,liczbę
losową”.
7.2. Czas dyskretny, przestrzeń ciągła
Przypadek ciągłej lub raczej ogólnej przestrzeni stanów jest w istocie równie
prosty, tylko oznaczenia trzeba trochę zmienić i sumy zamienić na całki.
Dla prostoty przyjmijmy, że ![]() . Poniżej sformułujemy definicję w taki sposób, żeby podkreślić analogię do przypadku dyskretnego i pominiemy subtelności teoretyczne.
Zwróćmy tylko uwagę, że prawdopodobieństwo warunkowe nie może tu być zdefiniowane tak elementarnie jak w Definicji 7.1, bo zdarzenie warunkujące może mieć prawdopodobieństwo zero.
. Poniżej sformułujemy definicję w taki sposób, żeby podkreślić analogię do przypadku dyskretnego i pominiemy subtelności teoretyczne.
Zwróćmy tylko uwagę, że prawdopodobieństwo warunkowe nie może tu być zdefiniowane tak elementarnie jak w Definicji 7.1, bo zdarzenie warunkujące może mieć prawdopodobieństwo zero.
Definicja 7.2
(i)
Ciąg ![]() zmiennych losowych o wartościach w
zmiennych losowych o wartościach w ![]() nazywamy łańcuchem Markowa, jeśli dla każdego
nazywamy łańcuchem Markowa, jeśli dla każdego
![]() , dla każdego ciągu
, dla każdego ciągu ![]() punktów
przestrzeni
punktów
przestrzeni ![]() oraz dowolnego (borelowskiego ) zbioru
oraz dowolnego (borelowskiego ) zbioru ![]() ,
,
(dla prawie wszystkich punktów ![]() ).
).
(ii) Łańcuch Markowa nazywamy jednorodnym, jeśli dla
dowolnego zbioru ![]() i każdego
i każdego ![]() możemy napisać
możemy napisać
(dla prawie wszystkich punktów ![]() ).
).
Funkcja ![]() , której argumentami są punkt
, której argumentami są punkt ![]() i zbiór
i zbiór ![]() , jest nazywana
jądrem przejścia. Ważne dla nas jest to, że dla ustalonego
, jest nazywana
jądrem przejścia. Ważne dla nas jest to, że dla ustalonego ![]() , jądro
, jądro ![]() rozważane jako funkcja zbioru jest rozkładem prawdopodobieństwa.
W wielu przykładach jest to rozkład zadany przez gęstość,
rozważane jako funkcja zbioru jest rozkładem prawdopodobieństwa.
W wielu przykładach jest to rozkład zadany przez gęstość,
Wtedy odpowiednikiem wzoru (7.1) jest następujący wzór na łączną gęstość:
| (7.4) |
gdzie ![]() jest gęstością rozkładu początkowego, zaś
jest gęstością rozkładu początkowego, zaś ![]() jest gęstością warunkową. Sformułowaliśmy Definicję 7.2 nieco ogólniej głównie dlatego, że w symulacjach ważną rolę odgrywają łańcuchy dla których prawdopodobieństwo przejścia nie ma gęstości. Przykładem może być łańcuch, który z niezerowym prawdopodobieństwem potrafi ,,stać w miejscu”, to znaczy
jest gęstością warunkową. Sformułowaliśmy Definicję 7.2 nieco ogólniej głównie dlatego, że w symulacjach ważną rolę odgrywają łańcuchy dla których prawdopodobieństwo przejścia nie ma gęstości. Przykładem może być łańcuch, który z niezerowym prawdopodobieństwem potrafi ,,stać w miejscu”, to znaczy
![]() , i ma prawdopodobieństwo przejścia postaci, powiedzmy
, i ma prawdopodobieństwo przejścia postaci, powiedzmy
Łańcuch Markowa na ogólnej przestrzeni stanów można rekurencyjnie generować w sposób opisany wzorem (7.3), to znaczy ![]() i
i ![]() dla
ciągu i.i.d.
dla
ciągu i.i.d. ![]() z rozkładu
z rozkładu ![]() .
Niech
.
Niech ![]() oznacza rozkład początkowy. Funkcje
oznacza rozkład początkowy. Funkcje ![]() i
i ![]() muszą spełniać warunki
muszą spełniać warunki
| (7.5) |
7.3. Czas ciągly, przestrzeń dyskretna
Rozważmy proces stochastyczny ![]() , czyli rodzinę zmiennych losowych o wartościach w skończonej przestrzeni stanów
, czyli rodzinę zmiennych losowych o wartościach w skończonej przestrzeni stanów ![]() , indeksowaną przez
parameter
, indeksowaną przez
parameter ![]() , który interpretujemy jako ciągły czas. Pojedyncze stany oznaczamy
przez
, który interpretujemy jako ciągły czas. Pojedyncze stany oznaczamy
przez ![]() lub podobnie. Załóżmy, że trajektorie są prawostronnie ciągłymi funkcjami mającymi lewostronne granice (prawie na pewno).
lub podobnie. Załóżmy, że trajektorie są prawostronnie ciągłymi funkcjami mającymi lewostronne granice (prawie na pewno).
Definicja 7.3
(i) Mówimy, że ![]() jest procesem Markowa, jeśli dla dowolnych
jest procesem Markowa, jeśli dla dowolnych ![]() oraz
oraz
![]() ,
,
(ii) Proces Markowa nazywamy jednorodnym, jeśli dla dowolnych stanów ![]() i
i ![]() i każdego
i każdego ![]() i
i ![]() możemy napisać
możemy napisać
to znaczy prawdopodobieństwo warunkowe w powyższym wzorze zależy tylko od ![]() ,
, ![]() i
i ![]() ,
ale nie zależy od
,
ale nie zależy od ![]() .
.
Sens założenia (i) jest taki sam jak w Definicji 7.1.
Żądamy mianowicie, żeby zmienna ![]() byłą warunowo niezależna od zmiennych
byłą warunowo niezależna od zmiennych
![]() pod warunkiem zdarzenia
pod warunkiem zdarzenia ![]() . Oczywiście,
. Oczywiście,
![]() jest prawdopodobieństwem przejścia w ciągu czasu
jest prawdopodobieństwem przejścia w ciągu czasu ![]() .
Rozkład początkowy oznaczymy przez
.
Rozkład początkowy oznaczymy przez ![]() .
Ponieważ
.
Ponieważ ![]() jest skończona,
jest skończona, ![]() może być przedstawiony jako wektor a
może być przedstawiony jako wektor a ![]() jako macierz.
jako macierz.
Odpowiednikiem macierzy przejścia jest macierz intensywności przejść zdefiniowana następująco.
gdzie ![]() jest macierzą identycznościową. Można udowodnić, że granice istnieją.
Tak więc
jest macierzą identycznościową. Można udowodnić, że granice istnieją.
Tak więc ![]() i
i ![]() przy
przy ![]() .
Innymi słowy,
.
Innymi słowy, ![]() jest rzeczywiście ,,intensywnością skoków z
jest rzeczywiście ,,intensywnością skoków z ![]() do
do ![]() ” (na jednostkę czasu). Mamy wzór analogiczny do (6.3):
” (na jednostkę czasu). Mamy wzór analogiczny do (6.3):
Zauważmy, że mamy ![]() . Wspomnijmy jeszcze mimochodem, że macierze przejścia wyrażają się przez macierz intensywności
. Wspomnijmy jeszcze mimochodem, że macierze przejścia wyrażają się przez macierz intensywności ![]() przy pomocy ,,macierzowej funkcji wykładniczej”:
przy pomocy ,,macierzowej funkcji wykładniczej”: ![]() . Dla uproszczenia notacji, niech
. Dla uproszczenia notacji, niech
![]() oznacza “intensywność wszystkich skoków ze stanu
oznacza “intensywność wszystkich skoków ze stanu ![]() ”.
”.
Z tego co zostało powiedziane łatwo się domyślić, że generowanie procesu Markowa
można zorganizować podobnie jak dla procesu Poissona, poprzez czasy skoków.
Niech ![]() będą kolejnymi momentami skoków,
będą kolejnymi momentami skoków,
Jeśli ![]() , to
czas oczekiwania na następny skok,
, to
czas oczekiwania na następny skok, ![]() zależy tylko od
zależy tylko od ![]() i ma
rozkład wykładniczy z parametrem
i ma
rozkład wykładniczy z parametrem ![]() . W szczególności, mamy
. W szczególności, mamy ![]() .
Jeśli obserwujemy proces w momentach skoków, czyli skupimy uwagę na ciągu
.
Jeśli obserwujemy proces w momentach skoków, czyli skupimy uwagę na ciągu
![]() to otrzymujemy łańcuch Markowa z czasem dyskretnym, nazywany
czasem ,,szkieletem”. Jego prawdopodobieństwa przejścia są takie:
to otrzymujemy łańcuch Markowa z czasem dyskretnym, nazywany
czasem ,,szkieletem”. Jego prawdopodobieństwa przejścia są takie:
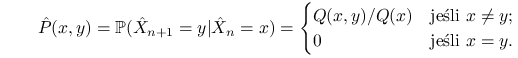 |
(7.6) |
Oczywiście, cała trajektoria procesu ![]() jest w pełni wyznaczona przez momenty skoków
jest w pełni wyznaczona przez momenty skoków
![]() i kolejne stany łańcucha szkieletowego
chain
i kolejne stany łańcucha szkieletowego
chain ![]() .
Po prostu,
.
Po prostu, ![]() dla
dla ![]() .
Następujący algorytm formalizuje opisany powyżej sposób generacji.
.
Następujący algorytm formalizuje opisany powyżej sposób generacji.
| Gen |
| for |
| begin |
| Gen |
| |
| Gen |
| end |
Czasami warto zmodyfikować algorytm w następujący sposób.
Generowanie procesu Markowa można rozbić na dwie fazy: najpierw wygenerować ,,potencjalne czasy
skoków” a następnie symulować ,,szkielet”, który będzie skakał wyłącznie w poprzednio
otrzymanych momentach (ale nie koniecznie we wszystkich spośród nich). Opiszemy dokładniej tę konstrukcję, która bazuje na własnościach procesu Poissona. Wyobraźmy sobie najpierw, że
dla każdego stanu ![]() symulujemy niezależnie jednorodny proces Poissona
symulujemy niezależnie jednorodny proces Poissona ![]() o punktach
skoku
o punktach
skoku ![]() przy czym ten proces ma intensywność
przy czym ten proces ma intensywność ![]() . Jeśli teraz, w drugiej fazie
. Jeśli teraz, w drugiej fazie ![]() , to za następny moment skoku wybierzemy
najbliższy punkt procesu
, to za następny moment skoku wybierzemy
najbliższy punkt procesu ![]() na prawo od
na prawo od ![]() , czyli
, czyli
![]() . Z własności procesu Poissona (patrz Stwierdzenie 6.2 i jego dowód) wynika, że zmienna
. Z własności procesu Poissona (patrz Stwierdzenie 6.2 i jego dowód) wynika, że zmienna ![]() ma rozkład wykładniczy z parametrem
ma rozkład wykładniczy z parametrem ![]() i metoda jest poprawna. Naprawdę nie ma nawet potrzeby generowania wszystkich procesów Poissona
i metoda jest poprawna. Naprawdę nie ma nawet potrzeby generowania wszystkich procesów Poissona ![]() . Warto posłużyć się metodą przerzedzania i najpierw
wygenerować jeden proces o dostatecznie dużej intensywności a następnie ,,w miarę potrzeby” go przerzedzać.
Niech
. Warto posłużyć się metodą przerzedzania i najpierw
wygenerować jeden proces o dostatecznie dużej intensywności a następnie ,,w miarę potrzeby” go przerzedzać.
Niech ![]() będzie procesem Poissona o intensywności
będzie procesem Poissona o intensywności ![]() i oznaczmy jego punkty skoków przez
i oznaczmy jego punkty skoków przez ![]() . Jeśli
w drugiej fazie algorytmu mamy
. Jeśli
w drugiej fazie algorytmu mamy ![]() w pewnym momencie
w pewnym momencie ![]() , to
zaczynamy przerzedzać proces
, to
zaczynamy przerzedzać proces ![]() w taki sposób, aby otrzymać proces o intensywności
w taki sposób, aby otrzymać proces o intensywności
![]() . Dla każdego punktu
. Dla każdego punktu ![]() ,
, ![]() powinniśmy rzucić monetą i z prawdopodobieństwem
powinniśmy rzucić monetą i z prawdopodobieństwem
![]() ten punkt usunąć. Ale jeśli usuniemy punkt
ten punkt usunąć. Ale jeśli usuniemy punkt ![]() to znaczy, że w tym punkcie
nie ma skoku, czyli
to znaczy, że w tym punkcie
nie ma skoku, czyli ![]() . Jeśli punkt
. Jeśli punkt ![]() zostawimy, to wykonujemy skok,
losując kolejny stan z prawdopodobieństwem
zostawimy, to wykonujemy skok,
losując kolejny stan z prawdopodobieństwem ![]() . W rezultacie, stan
. W rezultacie, stan ![]() jest wylosowany
z rozkładu prawdopodobieństwa
jest wylosowany
z rozkładu prawdopodobieństwa
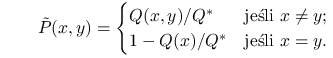 |
(7.7) |
Niech ![]() będzie ,,nadmiarowym szkieletem” procesu. Jest to łańcuch Markowa, który (w odróżnieniu od ,,cieńszego szkieletu”
będzie ,,nadmiarowym szkieletem” procesu. Jest to łańcuch Markowa, który (w odróżnieniu od ,,cieńszego szkieletu” ![]() ) może w jednym kroku pozostać w tym samym stanie i ma prawdopodobieństwa przejścia
) może w jednym kroku pozostać w tym samym stanie i ma prawdopodobieństwa przejścia ![]() .
.
Odpowiada temu następujący dwufazowy algorytm.
-
Faza I
| Gen |
-
Faza II
| Gen |
| for |
Algorytm jest bardzo podobny do metody wynalezionej przez Gillespie'go do symulowania
wielowymiarowych procesów urodzin i śmierci (głównie w zastosowaniach do chemii). Te procesy
mają najczęściej przestrzeń stanów postaci ![]() ; stanem układu jest
układ liczb
; stanem układu jest
układ liczb ![]() , gdzie
, gdzie ![]() jest liczbą osobników (na przykład cząstek) typu
jest liczbą osobników (na przykład cząstek) typu ![]() . Przestrzeń jest nieskończona, ale większa część rozważań przenosi się bez trudu.
Pojawia się tylko problem w ostatnim algorytmie jeśli
. Przestrzeń jest nieskończona, ale większa część rozważań przenosi się bez trudu.
Pojawia się tylko problem w ostatnim algorytmie jeśli ![]() , czego nie można wykluczyć. Zeby sobie z tym poradzić, można wziąć
, czego nie można wykluczyć. Zeby sobie z tym poradzić, można wziąć ![]() dostatecznie duże, żeby ,,na ogół” wystarczało,
a w mało prawdopodobnym przypadku zawitania do stanu
dostatecznie duże, żeby ,,na ogół” wystarczało,
a w mało prawdopodobnym przypadku zawitania do stanu ![]() z
z ![]() przerzucać się na
pierwszy, jednofazowy algorym.
przerzucać się na
pierwszy, jednofazowy algorym.




