Zagadnienia
4. Zbiory przybliżone
4.1. Zbiory przybliżone
4.1.1. Wprowadzenie do teorii zbiorów przybliżonych
4.1.1.1. Systemy informacyjne i tablice decyzyjne
-
Teoria zbiorów przybliżonych została wprowadzona w latach 80-tych przez prof. Zdzisława Pawlaka.
-
Głównym celem jest dostarczanie narzędzi dla problemu aproksymacji pojęć (zbiorów).
-
Zastosowania w systemach decyzyjnych:
-
Redukcja danych, selekcja ważnych atrybutów;
-
Generowanie reguł decyzyjnych;
-
Odkrywanie wzorców z danych: szablony, reguły asocjacyjne;
-
Odkrywanie zależności w danych.
-
Definicja
Jest to para ![]() , gdzie
, gdzie
-
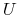 – skończony niepusty zbiór obiektów (ang. cases, states,
patients, observations …);
– skończony niepusty zbiór obiektów (ang. cases, states,
patients, observations …); -
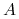 – skończony, niepusty zbiór atrybutów.
Każdy
– skończony, niepusty zbiór atrybutów.
Każdy 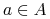 odpowiada pewnej funkcji
odpowiada pewnej funkcji 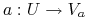 zwanej wartościowaniem, gdzie
zwanej wartościowaniem, gdzie 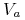 jest nazwana dziedziną atrybutu
jest nazwana dziedziną atrybutu 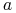 .
.
Dla ![]() , definiujemy
, definiujemy
-
 -sygnatura obiektu
-sygnatura obiektu 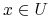 (ang.
(ang.  -information vector) jako
-information vector) jako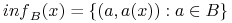
-
Zbiór sygnatur względem
 o obiektach z
o obiektach z 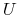 (ang.
(ang.  -information set):
-information set):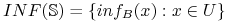
Tablica decyzyjna powstaje ze zwykłych tablic danych poprzez sprecyzowanie:
-
Atrybutów (nazwanych warunkowymi): cechy, których wartości na obiektach są dostępne, np. pomiary, parametry, dane osobowe, …
-
Decyzji (atrybut decyzyjny):, t.j. cecha “ukryta” związana z pewną znaną częściowo wiedzą o pewnym pojęciu:
-
Decyzja jest znana tylko dla obiektów z (treningowej) tablicy decyzyjnej;
-
Jest podana przez eksperta (np. lekarza) lub na podstawie późniejszych obserwacji (np. ocena giełdy);
-
Chcemy podać metodę jej wyznaczania dla dowolnych obiektów na podstawie wartości atrybutów warunkowych na tych obiektach.
-
4.5cm Przedstawiona tablica decyzyjna zawiera:
-
8 obiektów będących opisami pacjentów
-
3 atrybuty: Headache Muscle pain, Temp.
-
Decyzję stwierdzącą czy pacjent jest przeziębiony czy też nie. lub nie
8cm \example
| Ból głowy | Ból mięśni | Temp. | Grypa | |
|---|---|---|---|---|
| p1 | Tak | Tak | N | Nie |
| p2 | Tak | Tak | H | Tak |
| p3 | Tak | Tak | VH | Tak |
| p4 | Nie | Tak | N | Nie |
| p5 | Nie | Nie | H | Nie |
| p6 | Nie | Tak | VH | Tak |
| p7 | Nie | Tak | H | Tak |
| p8 | Nie | Nie | VH | Nie |
Dane są obiekty ![]() i zbiór atrybutów
i zbiór atrybutów ![]() ,
mówimy, że
,
mówimy, że
-
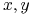 są rozróżnialne przez
są rozróżnialne przez  wtw, gdy istnieje
wtw, gdy istnieje 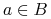 taki, że
taki, że 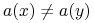 ;
; -
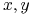 są nierozróżnialne przez
są nierozróżnialne przez  , jeśli one są
identyczne na
, jeśli one są
identyczne na  , tzn.
, tzn. 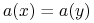 dla każdego
dla każdego 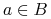 ;
; -
![[x]_{B}](wyklady/syd/mi/mi88.png) = zbiór obiektów nierozróżnialnych z
= zbiór obiektów nierozróżnialnych z 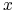 przez
przez  .
.
-
Dla każdych obiektów
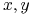 :
:-
albo
![[x]_{B}=[y]_{B}](wyklady/syd/mi/mi5.png) ;
; -
albo
![[x]_{B}\cap[y]_{B}=\emptyset](wyklady/syd/mi/mi50.png) .
.
-
-
Relacja
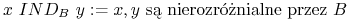
jest relacją równoważności.
-
Każdy zbiór atrybutów
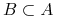 wyznacza podział
zbioru obiektów na klasy nierozróżnialności.
wyznacza podział
zbioru obiektów na klasy nierozróżnialności.
Dla ![]()
4.5cm
-
obiekty
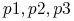 są nierozróżnialne;
są nierozróżnialne; -
są 3 klasy nierozróżnialności relacji
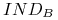 :
: -
8cm \example
| Ból głowy | Ból mięśni | Temp. | Grypa | |
|---|---|---|---|---|
| p1 | Tak | Tak | N | Nie |
| p2 | Tak | Tak | H | Tak |
| p3 | Tak | Tak | VH | Tak |
| p4 | Nie | Tak | N | Nie |
| p5 | Nie | Nie | H | Nie |
| p6 | Nie | Tak | VH | Tak |
| p7 | Nie | Tak | H | Tak |
| p8 | Nie | Nie | VH | Nie |
-
Każdy zbiór obiektów
 (np. klasa decyzyjna, pojęcie) może być
opisany za pomocą atrybutów ze zbioru
(np. klasa decyzyjna, pojęcie) może być
opisany za pomocą atrybutów ze zbioru  dokładnie lub w
przybliżeniu
dokładnie lub w
przybliżeniu
-
dokładny opis: jeśli
 jest sumą pewnych klas nierozróznialności
definiowanych przez
jest sumą pewnych klas nierozróznialności
definiowanych przez  (ZBIORY DOKŁADNE)
(ZBIORY DOKŁADNE) -
przybliżony opis: w przeciwnym przypadku (ZBIORY PRZYBLIŻONE)
-
-
W obu przypadkach
 może być opisany przez 2 “dokładne
zbiory” zwane dolną i górną aproksymacją zbioru
może być opisany przez 2 “dokładne
zbiory” zwane dolną i górną aproksymacją zbioru 
![\underline{B}(X)=\{ x:[x]_{B}\subset X\}\quad\overline{B}(X)=\{ x:[x]_{B}\cap X\neq\emptyset\}](wyklady/syd/mi/mi206.png)
-
Obszar brzegowy (ang.
 -boundary region) pojęcia
-boundary region) pojęcia  zawiera obiekty, dla
których nie możemy jednoznacznie zdecydować czy należą one do
zawiera obiekty, dla
których nie możemy jednoznacznie zdecydować czy należą one do  czy nie na podstawie
atrybutów z
czy nie na podstawie
atrybutów z 
-
Obszar wewnętrzny (ang.
 -inside region of X) zawiera obiekty, które
możemy pewnie klasyfikować jako elementy pojęcia
-inside region of X) zawiera obiekty, które
możemy pewnie klasyfikować jako elementy pojęcia  mając do dyspozycji atrybuty z
mając do dyspozycji atrybuty z  .
. -
Zbiór jest przybliżony (ang. rough set) jeśli obszar brzegowy jest niepusty, w przeciwnym przypadku zbiór jest nazwany dokładny (ang. crisp set).
6cmNiech ![]() <2->
\onslide
<2->
\onslide
<3-> Chcemy aproksymować pojęcie definiowane przez klasę decyzyjną (play=no)
<4-> Aproksymacje pojęcia ![]() :
:
<5-> Reguła pewna:
![]()
5.4cm
\onslide<1->
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ID
![]()
outlook
temp.
hum.
windy
![]()
play
1
![]()
sunny
hot
high
FALSE
![]()
no
2
![]()
sunny
hot
high
TRUE
![]()
no
3
![]()
overcast
hot
high
FALSE
![]()
yes
4
![]()
rainy
mild
high
FALSE
![]()
yes
5
![]()
rainy
cool
normal
FALSE
![]()
yes
6
![]()
rainy
cool
normal
TRUE
![]()
no
7
![]()
overcast
cool
normal
TRUE
![]()
yes
8
![]()
sunny
mild
high
FALSE
![]()
no
9
![]()
sunny
cool
normal
FALSE
![]()
yes
10
![]()
rainy
mild
normal
FALSE
![]()
yes
11
![]()
sunny
mild
normal
TRUE
![]()
yes
12
![]()
overcast
mild
high
TRUE
![]()
yes
13
![]()
overcast
hot
normal
FALSE
![]()
yes
14
![]()
rainy
mild
high
TRUE
![]()
no
<5-> Reguły przybliżone:
Jakość aproksymacji (ang. accuracy of approximation)
-
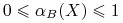
-
Jeśli
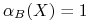 , to zbiór
, to zbiór  jest dokładnie definiowany przez
jest dokładnie definiowany przez
 ;
; -
Jeśli
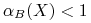 , to zbiór
, to zbiór  jest aproksymacyjnie definiowany przez
jest aproksymacyjnie definiowany przez
 ;
;
4.1.1.2. Redukty
-
W systemach decyzyjnych, nie wszystkie atrybuty są potrzebne do procesie podejmowania decyzji;
-
Chcemy wybrać pewne podzbiory atrybutów niezbędnych do tego celu;
-
Redukty to minimalne podzbiory atrybutów zachowujących charakterystykę całego zbioru atrybutów.
-
W teorii zbiorów przybliżonych, istnieją co najmniej 2 pojęcia reduktów: informacyjne i decyzyjne.
Definicja reduktu informacyjnego
Zbiór atrybutów ![]() nazywamy reduktem tablicy decyzyjnej
nazywamy reduktem tablicy decyzyjnej ![]() wtw, gdy
wtw, gdy
-
 zachowuje rozróżnialność zbioru A:
zachowuje rozróżnialność zbioru A:t.j. dla dowolnych obiektów
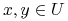 ,
,jeśli
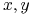 są rozróżnialne przez
są rozróżnialne przez 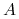 , to są również rozróżnialne
przez
, to są również rozróżnialne
przez 
-
 jest niezredukowalny:
jest niezredukowalny:tzn. żaden właściwy podzbiór
 nie zachowuje rozróżnialności
zbioru
nie zachowuje rozróżnialności
zbioru 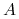 (t.j.,
(t.j.,  jest minimalny pod względem rozróżnialności)
jest minimalny pod względem rozróżnialności)
Definicja reduktu decyzyjnego
Zbiór atrybutów ![]() nazywamy reduktem tablicy
nazywamy reduktem tablicy ![]() wtw, gdy
wtw, gdy
-
 zachowuje rozróżnialność zbioru
zachowuje rozróżnialność zbioru 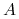 względem decyzji
względem decyzji 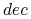 :
:t.j. dla dowolnych obiektów
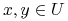 ,
,jeśli
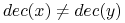 i
i 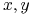 są rozróżnialne przez
są rozróżnialne przez 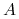 , to są również rozróżnialne
przez
, to są również rozróżnialne
przez 
-
 jest niezredukowalny:
jest niezredukowalny:tzn. żaden właściwy podzbiór
 nie zachowuje rozróżnialności
zbioru
nie zachowuje rozróżnialności
zbioru 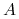 (
( jest minimalny pod względem rozróżnialności)
jest minimalny pod względem rozróżnialności)
-
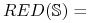 zbiór wszystkich reduktów tablicy
decyzyjnej
zbiór wszystkich reduktów tablicy
decyzyjnej 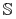 ;
; -
Jeśli
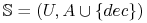 i
i 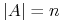 to
to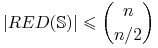
-
rdzeń: zbiór atrybutów będących we wszystkich reduktach

-
Znaleźć rdzeń danej tablicy decyzyjnej;
-
Znaleźć jakiś redukt;
-
Znaleźć krótkie redukty;
-
Znaleźć długie redukty.
4.1.2. Złożoność problemu szukania reduktów
\onslide<1-2> Problem najkrótszego reduktu \block
- Dane:
-
Tablica decyzyjna
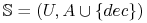 ;
;
- Szukane:
-
“najkrótszy redukt tablicy decyzyjnej
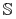 ”, tzn.
taki redukt decyzyjny
”, tzn.
taki redukt decyzyjny 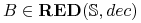 , że
, że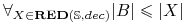
<2> Twierdzenie Problem szukania najkrótszego reduktu jest NP-zupełny. \block
-
<+-| alert@+> Ogólnie musimy pokazać, że jakiś znany NP-zupełny problem jest “łatwiejszy” od problemu najkrótszego reduktu;
-
<+-| alert@+> Wybierzmy problem minimalnego pokrycia wierzchołkami:
“Dany jest graf
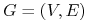 . Znaleźć minimalny zbiór
wierzchołków
. Znaleźć minimalny zbiór
wierzchołków 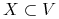 o takiej własności, że każda krawędź
z
o takiej własności, że każda krawędź
z 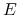 posiada co najmniej jeden z końców w
posiada co najmniej jeden z końców w  .”
.” -
<+-| alert@+> Wielomianowa transformacja:
\onslide<4->

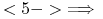 \onslide
\onslide
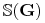
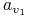
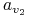
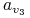
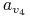
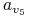
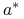
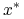
0 0 0 0 0 0 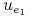
1 1 0 0 0 1 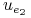
1 0 0 1 0 1 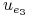
0 1 0 0 1 1 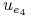
0 1 0 1 0 1 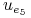
1 0 1 0 0 1 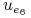
0 0 1 0 1 1
-
<+-> Można też pokazać, że problem najkrótszego reduktu jest “łatwiejszy” niż znany problem “Minimal Hitting Set” (minimalny zbiór przecinający?)
-
Dane: Zbiór
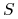 i rodzina jego podzbiorów
i rodzina jego podzbiorów 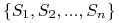 .
Zbiór
.
Zbiór 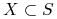 nazywamy zbiórem przecinającym, jeśli
nazywamy zbiórem przecinającym, jeśli  ma niepuste
przecięcie z każdym ze zbiorów
ma niepuste
przecięcie z każdym ze zbiorów 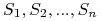 .
. -
Szukane: minimalny zbiór przecinający.
-
-
<+-> Te problemy są obliczeniowo równoważne!
Czyli każdy algorytm dla jednego problemu można przeksztalcić w czasie wielomianowym na odpowiedni algorytmu dla drugiego problemu, który posiada te same cechy zlożonościowe.




