Zagadnienia
5. Wnioskowanie Boolowskie w obliczaniu reduktów i reguł decyzyjnych
5.1. Wnioskowanie Boolowskie w obliczaniu reduktów i reguł decyzyjnych
5.1.1. Metody wnioskowań Boolowskich w szukaniu reduktów
5.1.1.1. Algebry Boola
\columns\column9cm Algebra Boola Jest to struktura algebraiczna \definition
spełniająca następujące aksjomaty
- Przemienność:
![]()
![]()
- Rozdzielność:
![]()
![]()
- Elementy neutralne:
![]()
- Istnienie elementu komplementarnego:
![]()
*) Czasem negacja jest dodana do sygnatury algebry Boola.
-
<+-> Algebra zbiorów:
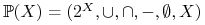 ;
; -
<+-> Rachunek zdań
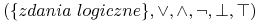
-
<+-> Binarna algebra Boola
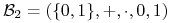 to jest najmniejsza, ale najważniejsza algebra Boola w zastosowaniu.
to jest najmniejsza, ale najważniejsza algebra Boola w zastosowaniu.![\begin{array}[]{c|c|c|c}x&y&x+y&x\cdot y\\
\hline 0&0&0&0\\
0&1&1&0\\
1&0&1&0\\
1&1&1&1\\
\hline\end{array}\qquad\begin{array}[]{c|c}x&\neg x\\
\hline 0&1\\
1&0\\
\end{array}](wyklady/syd/mi/mi358.png)
Przykłady zastosowań:
-
projektowanie układów scalonych;
-
rachunek zdań.
-
- Łączność (ang. Associative law):
-
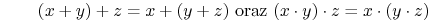
- Idempotence:
-
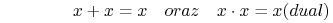
- Działania z 0 i 1:
-
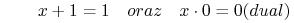
- Pochłanienie (ang. Absorption laws):
-
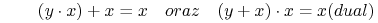
- Inwolocja (ang. Involution laws):
-
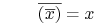
- Prawa DeMorgana (ang. DeMorgan's laws):
-
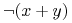
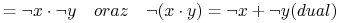
- Prawa konsensusu (ang. Consensus laws):
-
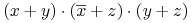
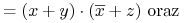
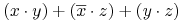
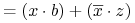
- Zasada dualności:
-
Każda algebraiczna równość pozostaje prawdziwa jeśli zamieniamy operatory
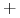 na
na  ,
,  na
na 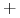 , 0 na 1 oraz 1 na 0.
, 0 na 1 oraz 1 na 0.
5.1.1.2. Funkcje Boolowskie i wnioskowanie Boolowskie
-
<+-> Każde odwzorowanie
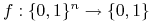 nazywamy (zupełną) funkcją Boolowską.
nazywamy (zupełną) funkcją Boolowską. -
<+-> Funkcje Boolowskie
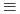 formuły Boolowskie:
formuły Boolowskie:-
Stałe, zmienne, operatory
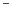 ,
, 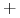 oraz
oraz 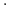
-
Literały, mintermy (jednomiany), maxtermy, …
-
Kanoniczna postać dyzjunkcyjna (DNF), np.
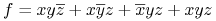 ;
; -
Kanoniczna postać koniunkcyjna (CNF), np.
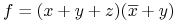
-
-
<+-> Term
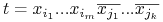 nazywamy implikantem funkcji
nazywamy implikantem funkcji 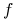 jeśli
jeśli 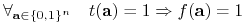
-
<+-> Implikant pierwszy: jest to implikant, który przestaje nim być po usunięciu dowolnego literału.
-
<+-> Kanoniczna postać Blake'a: każdą funkcję Boolowską można przedstawić jako sumę wszystkich jej imlikantów pierwszych:
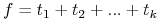
Wiele formuł reprezentuje tę samą funkcję;
![]()
![]()
![]()
![]() jest implikantem
jest implikantem
![]() jest implikantem pierwszym
jest implikantem pierwszym
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
-
<+-> Niech
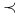 oznacza relację częściowego porządku w
oznacza relację częściowego porządku w 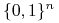
-
<+-> Funkcja
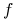 jest monotoniczna (niemalejąca) wtw, gdy dla każdych
jest monotoniczna (niemalejąca) wtw, gdy dla każdych
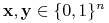 jeśli
jeśli 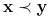 to
to 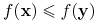
-
<+-> monotoniczne funkcje Boolowskie można zapisać bez użycia negacji.
-
<+-> term
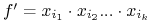 nazywamy
implikantem pierwszym funkcji monotonicznej
nazywamy
implikantem pierwszym funkcji monotonicznej 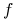 jeśli
jeśli-
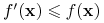 dla każdego wektora
dla każdego wektora 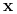 (jest implikantem)
(jest implikantem) -
każda funkcja większa od
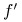 nie jest implikantem
nie jest implikantem
-
-
<+-> Np. funkcja
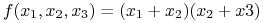
posiada 2 implikanty pierwsze:
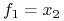 i
i 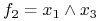
-
Modelowanie: Kodowanie problemu za pomocą układu równań Boolowskich;
-
Redukcja: Sprowadzenie układu równań do pojedynczego równania postaci
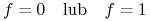
-
Konstrukcja: Znalezienie wszystkich implikantów pierwszych funkcji
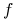 (konstrukcja kanonicznej postaci Blake'a);
(konstrukcja kanonicznej postaci Blake'a); -
Dedukcja: Zastosowanie pewnej sekwencji wnioskowań transformujących implikanty pierwsze do rozwiązań problemu.
6cm <1-> \onslide
Problem:
![]() are considering going to a party. Social constrains:
are considering going to a party. Social constrains:
-
If A goes than B won't go and C will;
-
If B and D go, then either A or C (but not both) will go
-
If C goes and B does not, then D will go but A will not.
<2-> Problem modeling:
6cm
-
<3-> After reduction:
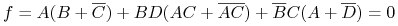
-
<4-> Blake Canonical form:
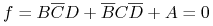
-
<5-> Facts:
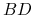
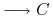
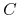
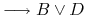
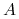
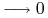
-
<6-> Reasoning: (theorem proving)
e.g., show that
”nobody can go alone.”
7cm
-
<+-> Problem SAT: czy równanie
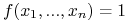
posiada rozwiązanie?
-
<+-> SAT odgrywa ważną rolę w teorii złożoności (twierdzenie Cooka, dowodzenie NP-zupełności …)
-
<+-> Każdy SAT-solver może być używany do rozwiązywania problemu planowania.
-
<+-> Blocks world problem: Po redukcji formuła boolowska nadal zawiera
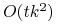 zmiennych i
zmiennych i 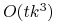 klauzuli (
klauzuli (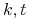 - liczby bloków i kroków).
- liczby bloków i kroków). -
<+-> Np. Dla
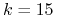 ,
, 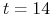 , mamy 3016 zmiennych i 50457 klausuli
, mamy 3016 zmiennych i 50457 klausuli
5cm<4->\only
<3->
-
<+-> Konstrukcja funkcji odróżnialności:
-
Zmienne boolowskie: atrybuty
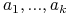 ;
; -
Klauzula:
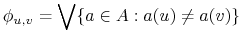
-
Funkcja rozróżnialności:
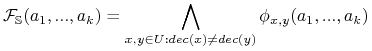
-
-
<+-> przekształcenie funkcji rozróżnialności do postaci DNF
-
<+-> każdy implikant pierwszy odpowiada jednemu reduktowi;
| Hurt. | Jakość obsługi | Jakość towaru | Obok autostrady? | Centrum? | decyzja |
|---|---|---|---|---|---|
| ID | |||||
| 1 | dobra | dobra | nie | nie | strata |
| 2 | dobra | dobra | nie | tak | strata |
| 3 | bdb | dobra | nie | nie | zysk |
| 4 | slaba | super | nie | nie | zysk |
| 5 | slaba | niska | tak | nie | zysk |
| 6 | slaba | niska | tak | tak | strata |
| 7 | bdb | niska | tak | tak | zysk |
| 8 | dobra | super | nie | nie | strata |
| 9 | dobra | niska | tak | nie | zysk |
| 10 | slaba | super | tak | nie | zysk |
| 11 | dobra | super | tak | tak | zysk |
| 12 | bdb | super | nie | tak | zysk |
| 13 | bdb | dobra | tak | nie | ? |
| 14 | slaba | super | nie | tak | ? |
| 1 | 2 | 6 | 8 | |
|---|---|---|---|---|
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 7 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 |
-
<+-> usuwanie alternatyw regułą pochłaniania (t.j.
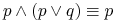 ):
):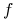
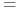
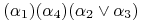
-
<+-> sprowadzanie funkcji
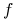 z postaci CNF (koniunkcja alternatyw) do postaci
DNF (alternatywa koniunkcji)
z postaci CNF (koniunkcja alternatyw) do postaci
DNF (alternatywa koniunkcji)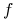
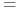
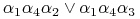
-
<+-> Każdy składnik jest reduktem! Zatem mamy 2 redukty:
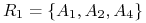 i
i 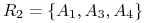
5.1.1.3. Heurystyka Johnsona
-
<+-> Atrybut jest ważniejszy jeśli częściej występuje w klauzulach;
-
<+-> Selekcja: W każdym kroku wybierzmy atrybut, który najczęściej występuje w funkcji rozróżnialności;
-
<+-> Usuwanie: Usuwamy z tej funkcji te klauzule, które zawierają wybrany atrybut;
-
<+-> Powtarzamy Selekcja i Usuwanie dopóty, póki funkcja rozróżnialności zawiera jeszcze jakąś klazulę.
Heurystyka Johnsona
-
Znaleźć atrybut, który występuje najczęściej w macierzy rozróżnialności;
-
Usuwnąć wszystkie pola zawierające wybrany atrybut;
-
Powtarzamy kroki 1 i 2 dopóki wszystkie pola macierzy są puste.
| 1 | 2 | 6 | 8 | |
|---|---|---|---|---|
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 7 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 |
-
W macierzy nierozróznialności z poprzedniego przykładu

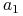 - występuje 23 razy
- występuje 23 razy 
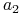 - występuje 23 razy
- występuje 23 razy
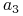 - występuje 18 razy
- występuje 18 razy 
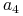 - występuje 16 razy
- występuje 16 razy -
Jeśli wybieramy
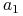 , to po usunięciu pól zawierających
, to po usunięciu pól zawierających 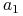 zostało 9
niepustych pól macierzy nierozróżnialności. Wśród nich:
zostało 9
niepustych pól macierzy nierozróżnialności. Wśród nich: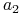 - występuje 7 razy
- występuje 7 razy 
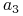 - występuje 7 razy
- występuje 7 razy 
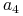 - występuje 6 razy
- występuje 6 razy -
Jeśli wybieramy tym razem
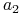 to zostały 2 niepuste pola i wśród nich
to zostały 2 niepuste pola i wśród nich
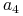 jest zdecydowanym faworytem.
jest zdecydowanym faworytem. -
Możemy dostać w ten sposób redukt:
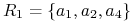 .
.
-
Niech
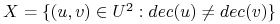 ;
; -
Niech
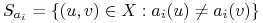 ;
; -
Niech
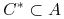 będzie minimalnym reduktem, lecz
będzie minimalnym reduktem, lecz
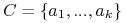 będzie reduktem znalezionym przez heurystykę
Johnsona;
będzie reduktem znalezionym przez heurystykę
Johnsona; -
Załóżmy, że heurystyka Johnsona musi płacić 1zł za każdym razem, gdy dodała
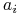 do
do 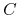 .
. -
Rozłóżmy ten koszt tym elementom, które zostały po raz pierwszy pokryte przez zbiór
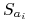
-
Niech
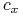 = koszt ponoszony przez
= koszt ponoszony przez 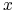 . Jeśli
. Jeśli 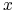 jest
pokryty po raz pierwszy przez
jest
pokryty po raz pierwszy przez 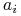 , to
, to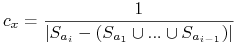
-
Heurystyka Johnsona ponosi łączny koszt
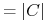 . Mamy
. Mamy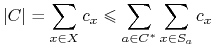
-
Gdybyśmy pokazali, że dla dowolnego altrybutu
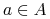
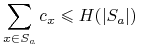
gdzie
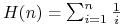 , wówczas możemy oszacować
dalej:
, wówczas możemy oszacować
dalej: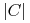
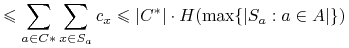
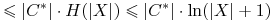
Lemat:
Dla dowolnego altrybutu ![]()
Dowód:
-
Niech
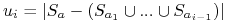 , mamy:
, mamy: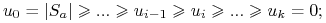
gdzie
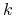 jest najmniejszym indeksem t., że
jest najmniejszym indeksem t., że 
-
Zatem
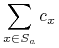
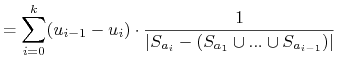
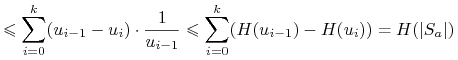
5.1.1.4. Inne heurystyki
-
ILP (Integer Linear Program)
-
Symulowane wyżarzanie (simulated annealing)
-
Algorytmy genetyczne
-
SAT solver
-
???
Dana jest funkcja ![]() zapisana w postaci CNF za pomocą zmiennych
zapisana w postaci CNF za pomocą zmiennych ![]()
-
Utwórz nowe zmienne
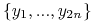 odpowiadające
literałom
odpowiadające
literałom 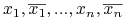 ;
; -
Dla każdej zmiennej
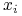 , utwórzmy nierówność
, utwórzmy nierówność 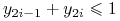
-
Zamień każdą klausulę
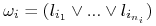 na
nierówność
na
nierówność 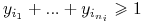 ;
; -
Utwórzmy układ nierówności z poprzednich punktów:
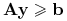
-
Zagadnienie programowania liniowego liczb całkowitych (ILP) jest definiowane jako problem szukania
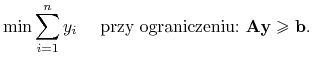
5.1.2. Systemy decyzyjne oparte o zbiory przybliżone
5.1.2.1. Reguły decyzyjne
Dla danego zbioru atrybutów ![]() definiujemy język deskryptorów jako trójkę
definiujemy język deskryptorów jako trójkę
gdzie
-
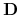 jest zbiorem deskryptorów
jest zbiorem deskryptorów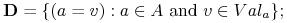
-
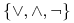 jest zbiorem standardowych operatorów logicznych;
jest zbiorem standardowych operatorów logicznych; -
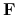 jest zbiorem formuł logicznych zbudowanych na deskryptorach z
jest zbiorem formuł logicznych zbudowanych na deskryptorach z
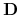 .
. -
Dla każdego zbioru atrybutów
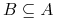 oznaczamy:
oznaczamy: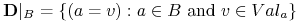 , czyli zbiór deskryptorów obciętych do
, czyli zbiór deskryptorów obciętych do  .
.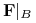 zbiór formuł zbudowanych na
zbiór formuł zbudowanych na 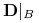 .
.
Semantyka:
Niech ![]() będzie tablicą informacyjną. Każda formuła
będzie tablicą informacyjną. Każda formuła ![]() , jest (semantycznie) skojarzona ze zbiorem
, jest (semantycznie) skojarzona ze zbiorem ![]() zawierającym obiekty spełniające
zawierającym obiekty spełniające ![]() .
.
Formalnie możemy indukcyjnie definiować semantykę jak następująco:
| (5.1) | ||||
| (5.2) | ||||
| (5.3) | ||||
| (5.4) |
Każda formuła ![]() może być charakteryzowana przez:
może być charakteryzowana przez:
-
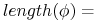 liczba deskryptorów w
liczba deskryptorów w 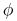 ;
; -
![support(\phi)=|[[\phi]]_{{\mathbb{S}}}|=](wyklady/syd/mi/mi350.png) liczba obiektów spełniających formułę
liczba obiektów spełniających formułę
Definicja reguł decyzyjnych
Niech ![]() będzie tablicą decyzyjną. Regułą decyzyjną dla
będzie tablicą decyzyjną. Regułą decyzyjną dla ![]() nazywamy formuły postaci:
nazywamy formuły postaci:
gdzie ![]() i
i ![]() .
.
Formułę ![]() nazywamy poprzednikiem (lub założeniem) reguły
nazywamy poprzednikiem (lub założeniem) reguły ![]() , a
, a ![]() nazywamy następnikiem (lub tezą) reguły
nazywamy następnikiem (lub tezą) reguły ![]() .
.
Oznaczamy poprzednik i następnik reguły ![]() przez
przez ![]() oraz
oraz
![]() .
.
Reguły atomowa: Są to reguły postaci:
| (5.5) |
Każda reguła decyzyjna ![]() postaci (5.5) może być charakteryzowana następującymi cechami:
postaci (5.5) może być charakteryzowana następującymi cechami:
|
|
liczba deskryptorów występujących w założeniu reguły |
|---|---|
|
|
nośnik reguły |
|
|
liczba obiektów z |
|
|
wiarygodność reguły |
Mówimy, że reguła ![]() jest niesprzeczna z
jest niesprzeczna z
![]() jeśli
jeśli
Minimalne niesprzeczne reguły:
Niech ![]() będzie daną tablicą decyzyjną. Niesprzeczną regułę
będzie daną tablicą decyzyjną. Niesprzeczną regułę
nazywamy minimalną niesprzeczną regułą decyzyjną jeśli usunięcie któregokolwiek z deskryptorów spowoduje, że
reguła przestaje być niesprzezcna z ![]() .
.
5.1.2.2. Regułowe systemy decyzyjne
Klasyfikatory regułowe dzialają w trzech fazach:
-
Faza treningu: Generuje pewien zbiór reguł
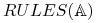 z danej tablicy decyzyjnej
z danej tablicy decyzyjnej 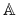 .
. -
Faza selekcji reguł: Szuka w
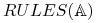 tych reguł, które są wspierane przez obiekt
tych reguł, które są wspierane przez obiekt 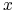 . Oznaczamy zbiór tych reguł
przez
. Oznaczamy zbiór tych reguł
przez
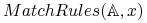 .
. -
Faza klasyfikacji: wyznacza klasędecyzyjną dla
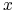 za pomocą reguł z
za pomocą reguł z
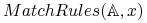 według następującego schematu:
według następującego schematu:-
Jeśli
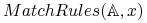 jest pusty: odpowiedź dla
jest pusty: odpowiedź dla 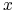 jest
jest 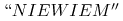 ,
tzn. nie mamy podstaw, aby klasyfikować obiekt
,
tzn. nie mamy podstaw, aby klasyfikować obiekt 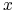 do którejkolwiek z klas;
do którejkolwiek z klas; -
Jeśli
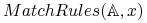 zawiera tylko obiekty z
zawiera tylko obiekty z 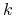 -tej klasy: wówczas
-tej klasy: wówczas
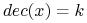 ;
; -
Jeśli
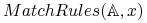 zawiera reguły dla różnych klas decyzyjnych:
wówczas decyzja dla
zawiera reguły dla różnych klas decyzyjnych:
wówczas decyzja dla 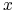 określimy za pomocą pewnego, ustalonego schematu głosowania
między regułami z
określimy za pomocą pewnego, ustalonego schematu głosowania
między regułami z 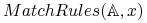 .
.
-
5.1.2.3. Szukanie minimalnych reguł decyzyjnych
-
Każda reguła powstaje poprzez skracanie opisu jakiegoś obiektu.
-
Redukty lokalne
-
Te same heurystyki dla reduktów decyzyjnych.
| Hurt. | Jakość obsługi | Jakość towaru | Obok autostrady? | Centrum? | decyzja |
|---|---|---|---|---|---|
| ID | |||||
| 1 | dobra | dobra | nie | nie | strata |
| 2 | dobra | dobra | nie | tak | strata |
| 3 | bdb | dobra | nie | nie | zysk |
| 4 | slaba | super | nie | nie | zysk |
| 5 | slaba | niska | tak | nie | zysk |
| 6 | slaba | niska | tak | tak | strata |
| 7 | bdb | niska | tak | tak | zysk |
| 8 | dobra | super | nie | nie | strata |
| 9 | dobra | niska | tak | nie | zysk |
| 10 | slaba | super | tak | nie | zysk |
| 11 | dobra | super | tak | tak | zysk |
| 12 | bdb | super | nie | tak | zysk |
| 13 | bdb | dobra | tak | nie | ? |
| 14 | slaba | super | nie | tak | ? |
| 1 | 2 | 6 | 8 | |
|---|---|---|---|---|
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 7 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 |
Reguły:
| 1 | 2 | 6 | 8 | |
|---|---|---|---|---|
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 7 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 |
Reguły:




