Zagadnienia

8.1 Sieci neuronowe
- 8.1.1 Sztuczne sieci neuronowe

8. Sieci neuronowe

8.1. Sieci neuronowe

8.1.1. Sztuczne sieci neuronowe

8.1.1.1. Inspiracje biologiczna/neurologiczna

<+-|alert@+> Podobnie jak symulowane wyżarzanie (SA) i algorytmy genetyczne (GA) sztuczne sieci neuronowe czerpią inspiracje ze zjawisk i procesów zachodzących w otaczającej nas przyrodzie.
<+-|alert@+> Techniki wykorzystywane przy tworzeniu sztucznych sieci neuronowych sa inspirowane wiedzą o mechanizmach myślenia zaczerpniętymi z fizjologii, neurologii i badań nad procesem poznawania (cognitive science).
<+-|alert@+>W układach nerwowych żywych organizmów stosunkowo proste elementy – neurony – współdziałając są w stanie realizować wysokopoziomowe, złożone funkcje.
<+-|alert@+> U podstaw sztucznych sieci neuronowych (ANN) leży idea wykorzystania prostych elementów obliczeniowych – sztucznych neuronów – do tworzenia układów zdolnych rozwiązywać skomplikowane zadania. Siła rozwiązania leży nie w samych elementach obliczeniowych, a w sposobie ich łączenia.
<+-|alert@+> Celem jest otrzymanie systemu, który przejawia cechy podobne do układu nerwowego.

Dawno, dawno temu – powstały neurony i układ nerwowy.
1868 – J.C. Maxwell opisał mechanizm sprzężenia zwrotnego.
1942 – N. Wiener formułuje podstawy współczesnej cybernetyki.
1943 – W.S. McCulloch i W.H. Pitts przedstawiają ideę działania sztucznego neuronu.
1949 – D.O. Hebb w dziele “The Organization of Behavior” opisuje zasadę (regułę Hebba), w oparciu o którą następuje adaptacja w sieciach neuronowych.
1957-1962 – Badania F. Rosenblatta nad pierwszymi fizycznymi modelami sieci neuronowych - perceptronami.
1960 – G. Widrow i M. Hoff przedstawiają pierwsze modele sieci jednowarstwowych – ADALINE/MADALINE.
1969 – M. Minsky i S. Pappert w książce “Perceptrons” poddają miażdzącej krytyce dotychczasowe osiagnięcia perceptroniki. Wykazują słabości i ograniczoność modelu jednowarstwowego. Rezultatem jest zawieszenie na niemal dekadę ok. 70% badań nad ANN.

Od 1972 – S. Amari, D. Grossberg, J. Anderson i inni – pierwsze badania nad samoorganizacją w sieciach neuronowych. Wykorzystanie sprzężenia zwrotnego do tworzenia układów naśladujących pamięć asocjacyjną u człowieka.
1974 – P. Werbos w swojej pracy doktorskiej podał ideę propagacji wstecznej (backpropagation), dzięki której możliwe stało sie opracowanie efektywnego mechanizmu adaptacji (uczenia się) w sieciach wielowarstwowych.
1982 – J. Hopfield przedstawia model sieci rekurencyjnej realizujacej zadania rozpoznawania wzorców i optymalizacji.
1986 – D.E. Rumelhart i J.L. McClelland w książce “Parallel Distributed Processing” opisali propagację wsteczną i sformułowali algorytm zmiany wag (regułe delty). Ich praca spowodowała rozpowszechnienie tych idei i w rezultacie lawinowy rozwój badań nad teorią i zastosowaniami ANN.

1990 – C. Mead przedstawia pierwsze analogowo-cyfrowe układy elektroniczne wykorzystujące architekture ANN. Pojawiają się poważne zastosowania w przemyśle i obronności.
1992 – T. Kohonen przedstawia ideę sieci z samoorganizacją (Self Organising Map – SOM) nazwanej potem jego imieniem. Opisuje także mechanizm uczenia sie kwantyzacji wektorów (Learning Vector Quantisation).
Od 1988 prowadzone są intensywne badania podstawowe i stosowane mające na celu podanie lepszych metod konstruowania, uczenia i oceny działania sieci neuronowych. Prowadzone są także badania nad podstawami teoretycznymi działania modelu ANN.
Dzień dzisiejszy – sztuczne sieci neuronowe sa uznanym i powszechnie stosowanym narzędziem w wielu działach nauki i techniki.

\columns\column

5cm

Masa ok. 1,5 kg - spora wariancja.
Objetość ok. 1600 cm3, powierzchnia ok. 2000 cm2 czyli niemal trzykrotnie więcej niż kula o tej samej objętości.
Kora - grubość 2-4 mm:

ok. 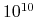$10^{{10}}$ komórek nerwowych;

ok. 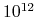$10^{{12}}$ komórek glejowych;

ok. 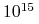$10^{{15}}$ połączeń (średnio 7000 na neuron).

\column

7.5cm

Nie znaleziono korelacji między rozmiarem mózgu a sprawnoscią intelektualną. Jest natomiast związek między rozmiarem kory a zdolnościami mózgu.

8.1.1.2. Perceptron

\columns\column

0.4

Potencjały odebrane z innych komórek za pomocą dendrytów są zbierane na błonie ciała komórki.
Gdy zebrane potencjały przekroczą wartość progową neuron staje sie aktywny i wysyła sygnały elektryczne (elektrochemiczne) przez akson.
Inne neurony odbierają sygnał zależnie od przepustowości synaps.

\column

0.6

Rozważmy najprotszy przypadek

$o=w_{{0}}+w_{{1}}x_{1}+\cdots+w_{n}x_{n}$

Szukajmy wektora ${\bf w}=(w_{1},...,w_{n})$ minimalizujące funkcję błędu:

$E[\vec{w}]\equiv\frac{1}{2}\sum _{{d\in D}}(t_{{d}}-o_{{d}})^{{2}}$

gdzie $D$ jest zbiorem przykładów treningowych.

\columns\column

0.6 Gradient

$\nabla E[\vec{w}]\equiv\left[\frac{\partial E}{\partial w_{{0}}},\frac{\partial E}{\partial w_{{1}}},\cdots\frac{\partial E}{\partial w_{{n}}}\right]$

\column

0.45 Alg. gradientu \block

Inicjalizujemy wagi neuronu (sieci) np. losowo.
Powtarzamy
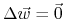- Inicjalizujemy $\Delta\vec{w}=\vec{0}$ ;
- Podajemy kolejny przykład 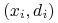$(x_{i},d_{i})$ do sieci i liczymy wartość 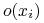$o(x_{i})$ ;
- Obliczamy błąd i poprawiamy wagi według reguły uczenia:
  
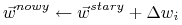
  $\vec{w}^{{nowy}}\leftarrow\vec{w}^{{stary}}+\Delta w_{i}$
  
  gdzie
  
  $\Delta\vec{w}=-\eta\nabla E[\vec{w}]$

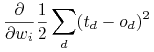$\displaystyle\frac{\partial E}{\partial w_{{i}}}$	$\displaystyle=$	$\displaystyle\frac{\partial}{\partial w_{{i}}}\frac{1}{2}\sum _{{d}}(t_{{d}}-o_{{d}})^{{2}}$
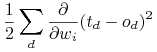	$\displaystyle=$	$\displaystyle\frac{1}{2}\sum _{{d}}\frac{\partial}{\partial w_{{i}}}(t_{{d}}-o_{{d}})^{{2}}$
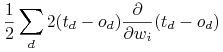	$\displaystyle=$	$\displaystyle\frac{1}{2}\sum _{{d}}2(t_{{d}}-o_{{d}})\frac{\partial}{\partial w_{{i}}}(t_{{d}}-o_{{d}})$
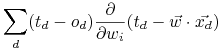	$\displaystyle=$	$\displaystyle\sum _{{d}}(t_{{d}}-o_{{d}})\frac{\partial}{\partial w_{{i}}}(t_{{d}}-\vec{w}\cdot\vec{x_{{d}}})$
$\displaystyle\frac{\partial E}{\partial w_{{i}}}$	$\displaystyle=$	$\displaystyle\sum _{{d}}(t_{{d}}-o_{{d}})(-x_{{i,d}})$

Pierwszym krokiem mającym naprawić niedoskonałości perceptronu, jest wprowadzenie nieliniowych, ciagłych i rózniczkowalnych funkcji aktywacji dla neuronów. Standardowo, stosuje się:

Logistyczna funkcje sigmoidalna (unipolarna):

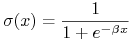
$\sigma(x)=\frac{1}{1+e^{{-\beta x}}}$

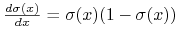o ważnej własności: $\frac{d\sigma(x)}{dx}=\sigma(x)(1-\sigma(x))$ .
Tangens hiperboliczny (bipolarny):

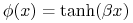
$\phi(x)=\tanh(\beta x)$

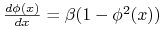o ważnej własności: $\frac{d\phi(x)}{dx}=\beta(1-\phi^{2}(x))$ .

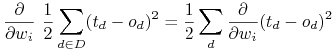$\displaystyle\frac{\partial E}{\partial w_{{i}}}$	$\displaystyle=$	$\displaystyle\frac{\partial}{\partial w_{{i}}}\ \frac{1}{2}\sum _{{d\in D}}(t_{{d}}-o_{{d}})^{{2}}=\frac{1}{2}\sum _{{d}}\frac{\partial}{\partial w_{{i}}}(t_{{d}}-o_{{d}})^{{2}}$
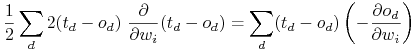	$\displaystyle=$	$\displaystyle\frac{1}{2}\sum _{{d}}2(t_{{d}}-o_{{d}})\ \frac{\partial}{\partial w_{{i}}}(t_{{d}}-o_{{d}})=\sum _{{d}}(t_{{d}}-o_{{d}})\left(-\frac{\partial o_{{d}}}{\partial w_{{i}}}\right)$
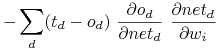	$\displaystyle=$	$\displaystyle-\sum _{{d}}(t_{{d}}-o_{{d}})\ \frac{\partial o_{{d}}}{\partial net_{{d}}}\ \frac{\partial net_{{d}}}{\partial w_{{i}}}$

Wiemy, że

	$\displaystyle\frac{\partial o_{{d}}}{\partial net_{{d}}}$	$\displaystyle=\frac{\partial\sigma(net_{{d}})}{\partial net_{{d}}}=o_{{d}}(1-o_{{d}})$
	$\displaystyle\frac{\partial net_{{d}}}{\partial w_{{i}}}$	$\displaystyle=\frac{\partial(\vec{w}\cdot\vec{x}_{{d}})}{\partial w_{{i}}}=x_{{i,d}}$

Więc

$\displaystyle\frac{\partial E}{\partial w_{{i}}}$

$\displaystyle=$

$\displaystyle-\sum _{{d\in D}}(t_{{d}}-o_{{d}})o_{{d}}(1-o_{{d}})x_{{i,d}}$

8.1.1.3. Warstwowe sieci neuronowe dla aproksymacji funkcji

Until satisfied, Do

For each training example, Do
1. Input the training example to the network and compute the network outputs \columns\column0.5 0.5 \column
2. For each output unit $k$
  
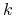
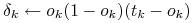
  $\delta _{{k}}\leftarrow o_{{k}}(1-o_{{k}})(t_{{k}}-o_{{k}})$
3. For each hidden unit $h$
  
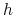
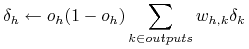
  $\delta _{{h}}\leftarrow o_{{h}}(1-o_{{h}})\sum _{{k\in outputs}}w_{{h,k}}\delta _{{k}}$
4. Update each network weight $w_{{i,j}}$
  
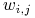
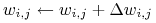
  $w_{{i,j}}\leftarrow w_{{i,j}}+\Delta w_{{i,j}}$
  
  where
  
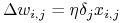
  $\Delta w_{{i,j}}=\eta\delta _{{j}}x_{{i,j}}$

8.1.1.4. Inne modele i zastosowania

Predykacja: Sieci neuronowe są często wykorzystywane, aby na podstawie pewnych danych wejściowych przewidywała dane wyjściowe. Wazną zaletą jest to, ze sieć może nauczyć się przewidywania sygnałów wyjściowych bez jawnego zdefiniowania związku między danymi wejściowymi a wyjściowymi. Tego typu układy są też często przydatne w zadaniach związanych ze sterowaniem.
Klasyfikacja i rozpoznawanie: Zadanie polega na przewidywaniu identyfikatora klasy, do której dany obiekt należy na podstawie wcześniej zaobserwowanych (nauczonych) przykładów..
Kojarzenie danych: Sieci neuronowe, dzięki zdolności uczenia się i uogólniania doświadczeń, pozwalają zautomatyzować procesy wnioskowania i pomagają wykrywać istotne powiązania pomiędzy danymi. Sieci neuronowe, dzięki zdolności uczenia się i uogólniania doświadczeń, pozwalają zautomatyzować procesy wnioskowania i pomagają wykrywać istotne powiązania pomiędzy danymi.

Analiza danych: Zadanie polega na znalezieniu związków pomiędzy danymi. Realizacja tego zadania przez sieci neuronowe daje nowe możliwości w zakresie prowadzenia analiz ekonomicznych.
Filtracja sygnałów Dane gospodarcze pochodzące z różnych źródeł są zakłócone. Klasyczne metody eliminacji “szumów” pozwalają usunąć zakłócenia o charakterze losowym, lecz nie dają podstaw do eliminacji przekłamań systematycznych.
Optymalizacja Sieci neuronowe - zwłaszcza sieci Hopfielda - dobrze nadają się do optymalizacji decyzji gospodarczych. Doświadczalnie potwierdzono możliwości sieci do rozwiązywania zadań optymalizacji statycznej i dynamicznej. Szczególnie ciekawe jest zastosowanie sieci do optymalizacji kombinatorycznej i zagadnień (NP)trudnych obliczeniowo, np. TSP.

Model sieci	Zastosowanie
Wielowarstwowa z propagacją wsteczną	Klasyfikacja
	Predykcja
Sieć rekurencyjna (Hopfielda)	Pamięć skojarzeniowa
Sieć konkurencyjna	PCA
samo-organizująca sieć (Kohonen)	Analiza skupień

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Systemy decyzyjne

Zagadnienia

8. Sieci neuronowe

8.1. Sieci neuronowe

8.1.1. Sztuczne sieci neuronowe

8.1.1.1. Inspiracje biologiczna/neurologiczna

8.1.1.2. Perceptron

8.1.1.3. Warstwowe sieci neuronowe dla aproksymacji funkcji

8.1.1.4. Inne modele i zastosowania