Zagadnienia
9. Teoria systemów uczących się
9.1. Teoria systemów uczących się
9.1.1. Wstęp do komputerowego uczenia się pojęć
-
Np. Pokazać, że dla każdego
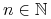 zachodzi
zachodzi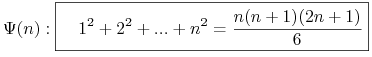
-
<+-> Indukcja pełna:
![\Psi(1)\quad\text{ oraz }\quad\forall _{{n\geq 1}}[\Psi(n)\implies\Psi(n+1)]](wyklady/syd/mi/mi650.png)
-
<+-> Indukcja niepełna: czy wystarczy sprawdzić, np.
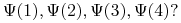
Podejście indukcyjne: Wnioskowanie na podstawie skończonego zbioru obserwacji
<2-> Jakie prawa rządzą procesem indukcyjnego uczenia się pojęć? <3-> Szukamy teorii obejmującej zagadnienia: \onslide\block
-
Szansy na skuteczne wyuczanie się pojęć;
-
Niezbędnej liczby przykładów treningowych;
-
Złożoności przestrzeni hipotez;
-
Jakości aproksymacji;
-
Metod reprezentacji danych treningowych;
-
<+-> Niech
-
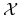 – (skończony lub nieskończony) zbiór obiektów;
– (skończony lub nieskończony) zbiór obiektów; -
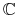 – klasa pojęć w
– klasa pojęć w 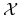 , tj.
, tj.
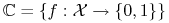
-
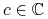 – pojęcie docelowe lub funkcja celu;
– pojęcie docelowe lub funkcja celu;
-
-
<+-> Dane są
-
skończona próbka etykietowanych obiektów:
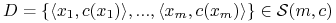
gdzie
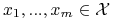 .
. -
przestrzeń hipotez
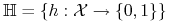 ;
;
-
-
<+-> Szukana
-
hipoteza
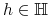 będąca dobrą aproksymacją pojęcia
będąca dobrą aproksymacją pojęcia 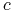 .
.
-
-
<+-> Wymagane
-
dobra jakość aproksymacji
-
szybki czas wyuczania.
-
0.65
-
<+-> Pojęcie: ”człowieka o średniej budowie ciała”.
-
<+-> Dane – czyli osoby – są reprezentowane przez ich wagę
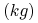 i wzrost
i wzrost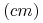 i są etykietowane przez
i są etykietowane przez 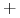 i
i  .
.
-
<+-> Dodatkowa wiedza: szukane pojęcie można wyrazić za pomocą PROSTOKĄTA
<7->
0.35\column\onslide<4->Uczenie prostokąta
\block
-
<+->
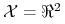 ;
; -
<+->
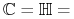 zbiór prostokątów;
zbiór prostokątów;
-
<+-> Przykład zbioru treningowego
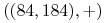 ,
, 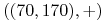 ,
, 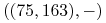 ,
, 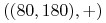 ,
,
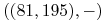 ,
, 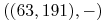 ,
, 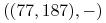 ,
, 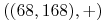
-
<+->
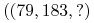
-
Uczenie półosi (lub dyskretyzacji):
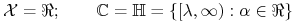
-
Uczenie hiperpłaszczyzny:
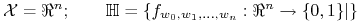
gdzie
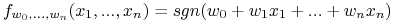 .
. -
Uczenie jednomianów Boolowskich:
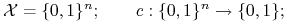
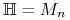 = zbiór jednomianów Boolowskich o
= zbiór jednomianów Boolowskich o 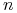 zmiennych.
zmiennych.
Błąd rzeczywisty
-
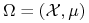 – przestrzeń
probabilistyczna na
– przestrzeń
probabilistyczna na 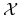 ;
; -
<+-> Błąd hipotezy
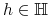 względem funkcji celu
względem funkcji celu 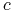 :
: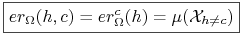
gdzie
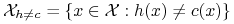 .
.
-
<+->[Statystyka:] Jeśli przykłady z
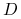 są wybrane zgodnie z miarą prawdopodobieństwa
są wybrane zgodnie z miarą prawdopodobieństwa 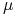 w sposób niezależny
oraz
w sposób niezależny
oraz  , to
, to-
<+->
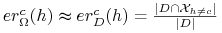 ,
, -
<+-> z prawdopodobieństwem
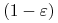
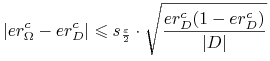
-
9.1.2. Model PAC (probably approximately correct)
\blockIdea modelu PAC (Probably Approximately
Correct): Określenie warunków, przy których uczeń (algorytm
uczenia się) z ,,dużym prawdopodobieństwem”
znajdzie ,,dobrą hipotezę” na podstawie danych ![]() .
.
<2>
PAC-owy uczeń Niech \block![]() będzie algorytmem uczenia się, jeśli
będzie algorytmem uczenia się, jeśli
dla każdych ![]() , istnieje
liczba
, istnieje
liczba ![]() taka, że dla dowolnego
pojęcia
taka, że dla dowolnego
pojęcia ![]() , dla dowolnego rozkładu
, dla dowolnego rozkładu ![]() na
na ![]() i dla
i dla ![]() mamy
mamy
Wówczas mówimy w skrócie, że ![]() jest PAC dla klasy
jest PAC dla klasy ![]() (“prawdopodobnie aproksymacyjnie poprawny”).
(“prawdopodobnie aproksymacyjnie poprawny”).
![]() = dopuszczalny poziom błędu;
= dopuszczalny poziom błędu; ![]() = poziom
zaufania.
= poziom
zaufania.
-
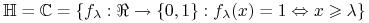
-
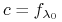
-
znaleźć
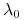 na podstawie losowo wygenerowanych przykładów
na podstawie losowo wygenerowanych przykładów
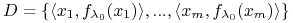
<2->Algorytm: \block
-
Set
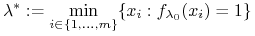 ;
; -
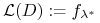 ;
;
<3-> Twierdzenie: Powyższy algorytm jest PAC \block
-
<+->
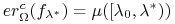 .
. -
<+->Niech
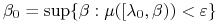 .
. -
<+-> Wówczas
![er_{{\Omega}}^{c}(f_{{\lambda^{*}}})\geqslant\varepsilon\Leftrightarrow\forall _{{x_{i}\in D}}:x_{i}\notin[\lambda _{0},\beta _{0}];](wyklady/syd/mi/mi630.png)
-
<+->Stąd
![\displaystyle\mu^{m}\{(x_{1},...,x_{m}):\forall _{{x_{i}\in D}}:x_{i}\notin[\lambda _{0},\beta _{0}]\}\leqslant(1-\varepsilon)^{m}](wyklady/syd/mi/mi733.png)
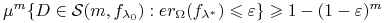
-
<+-> Aby to prawdopodobieństwo było
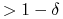 , wystarczy
przyjąć
, wystarczy
przyjąć 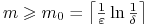
-
Niech
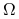 będzie rozkładem dyskretnym zdefiniowanym
przez
będzie rozkładem dyskretnym zdefiniowanym
przez 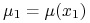 , …,
, …, 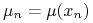 – dla pewnych
– dla pewnych
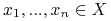 – takich, że
– takich, że 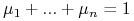 .
Niech
.
Niech 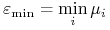 .
. -
Jeśli
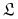 jest PAC, i jeśli
jest PAC, i jeśli 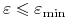 to warunek
to warunek 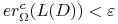 jest równoważny z
jest równoważny z 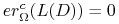 . Stąd dla każdego
. Stąd dla każdego
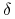 , istnieje
, istnieje 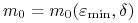 taka,
że dla dowolnego
taka,
że dla dowolnego 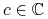 i
i 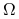
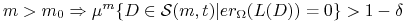
-
Wówczas mówimy, że prawdopodobnie
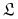 jest dokładnym algorytmem ( jest
PEC – probably exactly correct)
jest dokładnym algorytmem ( jest
PEC – probably exactly correct)
9.1.3. Wyuczalność klasy pojęć
-
<+-> Niech
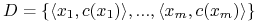 i niech
i niech
zbiór hipotez zgodnych z
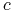 na próbce
na próbce 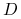 .
. -
<+->
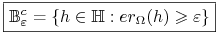 – zbiór
– zbiór 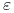 -złych hipotez
-złych hipotez
<4->
Definicja: Potencjalna wyuczalność
Mówimy, że \block![]() jest potencjalnie
wyuczalna za pomocą
jest potencjalnie
wyuczalna za pomocą ![]() , jeśli dla każdego rozkładu
, jeśli dla każdego rozkładu
![]() na
na ![]() i dowolnego pojęcia
i dowolnego pojęcia ![]() oraz dla dowolnych
oraz dla dowolnych ![]() istnieje
istnieje ![]() takie, że
takie, że
<1-> Algorytm ![]() nazywamy
niesprzecznym jeśli
nazywamy
niesprzecznym jeśli ![]() dla
każdego zbioru
dla
każdego zbioru ![]() .
.
Twierdzenie W przestrzeni potencjalnie wyuczalnej, każdy wzorowy uczeń (niesprzeczny algorytm) jest PAC-owy.
<2->
Twierdzenie (Haussler, 1988)
Jeśli ![]() i
i ![]() , to
, to
![]() jest potencjalnie wyuczalna.
jest potencjalnie wyuczalna.
Dowód: Niech ![]() (tzn.
(tzn.
![]() ). Wówczas
). Wówczas
Aby ![]() wystarczy wybrać
wystarczy wybrać
![]()
9.2. Wymiar Vapnika-Chervonenkisa
9.2.1. Wymiar Vapnika Chervonenkisa (ang. VC dimension)
-
<+-> Niech
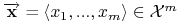 . Niech
. Niech
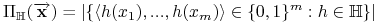
-
<+->
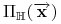 jest liczbą podziałów
zbioru elementów
jest liczbą podziałów
zbioru elementów 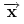 wyznaczonych przez
wyznaczonych przez
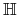 . Mamy
. Mamy 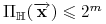 .
.
-
<+-> Gdy
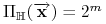 ,
mówimy, że
,
mówimy, że 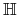 rozbija
rozbija 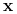 .
. -
<+-> Niech
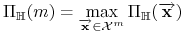
-
<+-> Na przykład: W przypadku klasy pojęć ”półosi” postaci
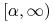 mamy
mamy
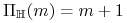 .
.
Uwagi:
-
<+-> Jeśli
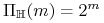 , to istnieje pewien zbiór o mocy
, to istnieje pewien zbiór o mocy 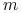 taki, że
taki, że
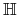 może definiować każdy jego podzbiór (
może definiować każdy jego podzbiór (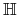 rozbija ten zbiór).
rozbija ten zbiór). -
<+-> Maksymalna wartość
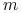 , dla której
, dla której 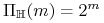 można
uważać za siłę wyrażalności przestrzeni
można
uważać za siłę wyrażalności przestrzeni 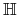
<3->
Definicja: wymiar \block![]() Wymiarem Vapnika-Chervonenkisa przestrzeni hipotez
Wymiarem Vapnika-Chervonenkisa przestrzeni hipotez ![]() nazywamy liczbę
nazywamy liczbę
gdzie maksimum wynosi ![]() jeśli ten zbiór jest nieograniczony.
jeśli ten zbiór jest nieograniczony.
0.7
-
<+->
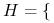 okręgi …
okręgi … 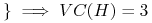
-
<+->
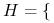 prostokąty …
prostokąty … 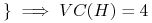
-
<+->
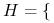 funkcje progowe …
funkcje progowe … 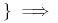
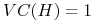 jeśli “+” są zawsze po prawej stronie;
jeśli “+” są zawsze po prawej stronie;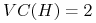 jeśli “+” mogą być po obu stronach
jeśli “+” mogą być po obu stronach -
<+->
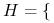 przedziały …
przedziały … 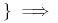
VC(H) = 2 jeśli “+” są zawsze w środku
VC(H) = 3 jeśli w środku mogą być zarówno “+” i “-”
-
<+->
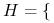 półpłaszczyzny w
półpłaszczyzny w 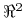 …
… 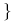
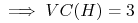
-
<+-> czy istnieje
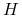 dla której
dla której 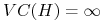 ?
?
0.3
Twierdzenie
Dla każdej liczby naturalnej ![]() , niech
, niech ![]() będzie perceptronem o
będzie perceptronem o ![]() wejściach rzeczywistych. Wówczas
wejściach rzeczywistych. Wówczas
Dowód:
-
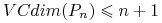 : Wynika z Twierdzenia Radona: Dla dowolnego zbioru
: Wynika z Twierdzenia Radona: Dla dowolnego zbioru 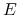 zawierającego
zawierającego 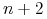 punktów w przestrzeni
punktów w przestrzeni 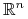 istnieje niepusty podzbiór
istnieje niepusty podzbiór 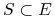 taki, że
taki, że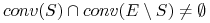
-
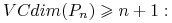 Wystarczy wybrać
Wystarczy wybrać 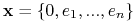 i pokazać, że każdy jego podzbiór jest definiowany przez jakiś perceptron.
i pokazać, że każdy jego podzbiór jest definiowany przez jakiś perceptron.
Twierdzenie
-
Jeśli
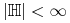 to
to 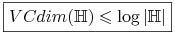 .
. -
<+-> (Lemat Sauer'a) Jeśli
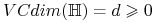 i
i
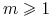 , to
, to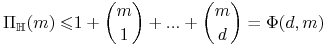
-
<+-> Wniosek:
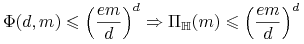
-
<+-> Jeśli
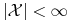 ,
, 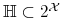 oraz
oraz 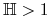
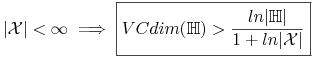
9.2.2. Podstawowe twierdzenia teorii uczenia się
\blockTwierdzenie: (Warunek konieczny)
Jeśli przestrzeń hipotez ma nieskończony wymiar ![]() to
nie jest potencjalnie wyuczalna.
to
nie jest potencjalnie wyuczalna.
<2-> Twierdzenie: (fundamentalne) Jeśli przestrzeń hipotez ma skończony wymiar VC, to jest ona potencjalnie wyuczalna. \block
-
<+-> Definiujemy
![Q^{{\varepsilon}}_{m}=\{ D\in\mathcal{S}(m,c):H^{c}[D]\cap B_{{\varepsilon}}\neq\emptyset\}](wyklady/syd/mi/mi734.png)
-
<+-> Szukamy górnego ograniczenia
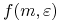 dla
dla 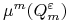 , które powinno
, które powinno- być niezależne od
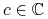 i
i 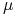 (rozkład).
(rozkład).- dążyć do 0 przy
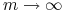
-
<+-> Twierdzenie Niech
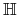 będzie przestrzenią
hipotez określonych na
będzie przestrzenią
hipotez określonych na  . Dla dowolnych
. Dla dowolnych 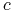 ,
, 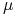 ,
, 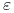 (ale
ustalonych) mamy
(ale
ustalonych) mamy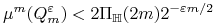
o ile
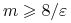 .
. -
<+-> Korzystamy z lematu Sauer'a, aby pokazać, że
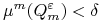 dla dostatecznie dużych
dla dostatecznie dużych 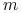 .
.
-
Dla skończonych przestrzeni hipotez
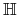 mamy
mamy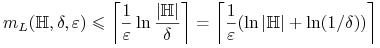
-
Twierdzenie Niech
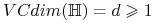 . Wówczas każdy
algorytm niesprzeczny
. Wówczas każdy
algorytm niesprzeczny 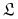 jest PAC oraz wymagana liczba przykładów
dla
jest PAC oraz wymagana liczba przykładów
dla 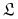 wynosi
wynosi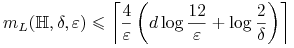
-
Dolne ograniczenia:
-
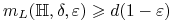
-
Jeśli
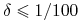 i
i 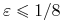 , to
, to 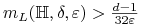
-
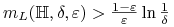
-
1. Wyuczalność Kiedy każdy ,,wzorowy uczeń” będzie PAC-owy?
2. Liczba przykładów Ile przykładów musi mieć uczeń, by się nauczyć?
<2->
Skończoność wymiaru \block![]()
-
<2->
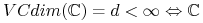 jest
wyuczalna;
jest
wyuczalna; -
<3-> Wówczas
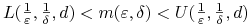
3. Ocena ucznia
na podstawie ![]() losowych przykładów
losowych przykładów
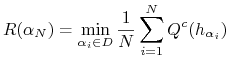 |
Kiedy i jak szybko ![]() ?
?
Skończoność wymiaru ![]()
-
<2->[3] Dla algorytmów typu ERM,
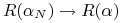 szybko.
szybko.
9.2.3. Appendix: ,,Nie ma nic za darmo” czyli “Non Free Lunch Theorem”
-
Znaleźć optimum nieznanej funkcji
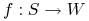 (
(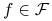 ), gdzie
), gdzie 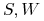 są skończonymi zbiorami.
są skończonymi zbiorami.
-
Działanie algorytmu przeszukiwania
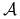 dla funkcji
dla funkcji 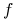 jest identyfikowany z wektorem:
jest identyfikowany z wektorem: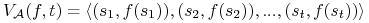
-
Ocena algorytmu:
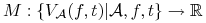 ;
;Np.
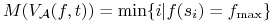
-
Warunek NFL: Dla dowolnej funkcji
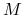 , i dla dowolnych algorytmów
, i dla dowolnych algorytmów 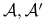
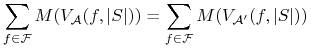
-
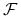 jest zamknięta wzg. permutacji: dla dowolnej funkcji
jest zamknięta wzg. permutacji: dla dowolnej funkcji 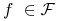 i
dowolnej permutacji
i
dowolnej permutacji 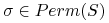 mamy
mamy 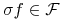
Twierdzenie o NFL
-
zachodzi równoważność
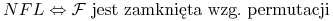
-
Prawdopodobieństwo wylosowania niepustej klasy funkcji zamkniętej wzg. permutacji wynosi:
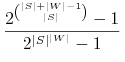
-
Algorytm
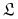 dobrze się uczy pojęcia
dobrze się uczy pojęcia 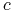 jeśli
jeśli 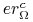 jest mały.
jest mały. -
Niech
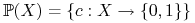 .
.Czy można stwierdzić wiedzieć, że
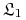 uczy się
wszystkich pojęć z
uczy się
wszystkich pojęć z 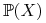 lepiej od
lepiej od 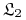 ?
? -
”No Free Lunch theorem” (Wolpert, Schaffer) w wersji problemów uczenia się głosi, że:
-
Żaden algorytm nie może być najlepszy w uczeniu wszystkich pojęć.
-
Każdy algorytm jest najlepszy dla takiej samej liczby pojęć
-
Ale interesuje nas tylko pewna klasa problemów czyli klasa pojęć
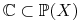
-
Wniosek: Należy znaleźć odp. algorytm do każdego problemu.
-




