Zagadnienia
1. Wprowadzenie do systemów decyzyjnych
1.1. Wprowadzenie do systemów decyzyjnych
1.1.1. Elementy systemów decyzyjnych
1.1.1.1. Wprowadzenie do teorii uczenia się
\blockKto się uczy? Ograniczymy się do programów komputerowych zwanych ”algorytmami uczącymi się”.
Czego się uczy?
-
pojęć: – np. odróżnienie “krzeseł” od innych mebli.
-
nieznanych urządzeń – np. używanie VCR
-
nieznanych środowisk – np. nowe miasto
-
procesów – np. pieczenie ciasta
-
rodzin podobnych wzorców – np. rozp. mowy, twarzy lub pisma.
-
funkcji: (np. funkcje boolowskie)
Wymagania skuteczność, efektywność, …
Każdy “uczeń” powinien mieć zdolność uogólnienia, t.j. zdolność rozpoznawania różnych obiektów tego samego pojęcia.
Np. jeśli uczymy się funkcji, to ważne jest aby “algorytm uczenia się” nie ograniczał się do jednej konkretnej funkcji. Żądamy aby “modele uczenia” działały skutecznie na klasach funkcji.
Uczeń może pozyskać informacje o dziedzinie poprzez:
-
Przykłady: Uczeń dostaje pozytywne i/lub negatywne przykłady. Przykłady mogą być zdobywane w sposób:
-
losowy: według pewnego znanego lub nieznanego rozkładu;
-
arbitralny;
-
złośliwy: (np. przez kontrolera, który chciałby wykryć sytuację, kiedy algorytm zachowuje się najgorzej);
-
specjalny przez życzliwego nauczyciela: (np., starającego ułatwiać proces uczenia się)
-
-
Zapytania: uczeń zdobywa informacje o dziedzinie przez zadawanie nauczycielowi zapytań.
-
Eksperymentowanie: aktywne uczenie się.
-
<+->Podejście indukcyjne: wnioskowanie na podstawie skończonego zbioru obserwacji;
-
<+-> Np. Pokazać, że dla każdego
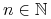
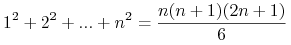
-
<+-> Jakie prawa rządzą w podejściu uczenia indukcyjnego?
Szukamy teorii pozwalającej na oszacowanie
-
Prawdopodobieństwa wyuczenia się pojęć;
-
Liczby niezbędnych przykładów treningowych;
-
Złożoności przestrzeni hipotez;
-
Skuteczności aproksymacji;
-
Jakość reprezentacji danych treningowych;
-
Skąd wiemy, czy uczeń się nauczył lub jak dobrze się nauczył?
-
Miara jakości wsadowa (ang. off-line, batch) i miara interaktywna (ang. on-line, interactive).
-
Jakość opisu vs. jakość predykcji
-
Skuteczność: obliczona na podstawie błędu klasyfikacji, dokładności opisu …
-
Efektywność uczenia: wymagana jest wielomianowa złożoność obliczeniowa.
-
Załóżmy, że chcemy nauczyć się pojęcia ”człowieka o średniej budowie ciała”. Dane – czyli osoby – są reprezentowane przez punkty
 i są etykietowane przez
i są etykietowane przez  dla pozytywnych
przykładów i
dla pozytywnych
przykładów i  dla negatywnych.
dla negatywnych. -
Dodatkowa wiedza: szukane pojęcie można wyrazić za pomocą PROSTOKĄTA
-
Na przykład dany jest etykietowany zbiór:
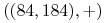 ,
, 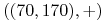 ,
, 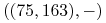 ,
, 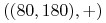 ,
, 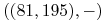 ,
,
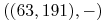 ,
, 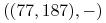 ,
, 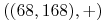
-
Znajdź etykietę
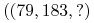
Roważany problem możemy zdefiniować problem następująco:
-
<+-> Cel: Znaleźć w
 prostokąt
prostokąt  o bokach równoległych do osi.
o bokach równoległych do osi. -
<+-> Wejście: Zbiór zawierający przykłady w postaci punktów
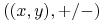 .
Punkty z tego zbioru zostały wygenerowane losowo.
.
Punkty z tego zbioru zostały wygenerowane losowo. -
<+-> Wyjście: Hipotetyczny prostokąt
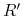 będący “'dobrą
aproksymacją”
będący “'dobrą
aproksymacją” 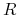 .
. -
<+-> Dodatkowe wymagania: Algorytm powinien być efektywny (ze wzgledu na złożoność obliczeniową) i powinien używać do uczenia jak najmniejszej liczby przykładów .
Przy ustalonych zbiorach pojęć ![]() (dotyczących obiektów ze zbioru
(dotyczących obiektów ze zbioru ![]() - skończonego lub nie) oraz hipotez
- skończonego lub nie) oraz hipotez ![]() rozważamy następujacy problem
rozważamy następujacy problem
-
<+-> Dane:
-
skończona próbka
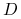 obiektów
obiektów 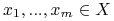 wraz z wartościami
pewnej funkcji
wraz z wartościami
pewnej funkcji 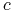 ze zbioru
ze zbioru 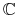 na tych obiektach;
na tych obiektach;
-
-
<+-> Szukane:
-
hipoteza
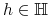 będąca dobrą aproksymacją pojęcia
będąca dobrą aproksymacją pojęcia 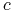 .
.
-
-
<+-> Żądania:
-
dobra jakość aproksymacji
-
szybki czas działania.
-
-
Uczenie półosi (lub dyskretyzacji):
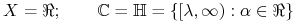
-
Uczenie hiperpłaszczyzny:
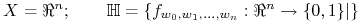
gdzie
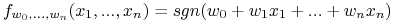 .
. -
Uczenie jednomianów Boolowskich:
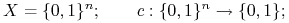
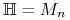 = zbiór jednomianów Boolowskich o
= zbiór jednomianów Boolowskich o 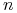 zmiennych.
zmiennych.
Niech
-
 – zbiór wszystkich obiektów.
– zbiór wszystkich obiektów.
-
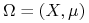 – przestrzeń probabilistyczna określona na
– przestrzeń probabilistyczna określona na  .
.
Błąd hipotezy ![]() względem pojęcia
względem pojęcia ![]() (funkcji docelowej):
(funkcji docelowej):
- Pytanie:
-
Dane jest pojęcie
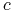 , hipoteza
, hipoteza 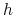 i zbiór przykladów
i zbiór przykladów 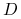 . Jak
oszacować rzeczywisty błąd hipotezy
. Jak
oszacować rzeczywisty błąd hipotezy 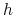 na podstawie jej błędu
na podstawie jej błędu 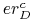 na zbiorze
na zbiorze 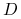 ?
? - Odp.:
-
Jeśli przykłady z
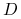 są wybrane zgodnie z miarą prawdopodobieństwa
są wybrane zgodnie z miarą prawdopodobieństwa 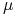 niezależnie od tej hipotezy i niezależnie od siebie nawzajem oraz
niezależnie od tej hipotezy i niezależnie od siebie nawzajem oraz
 , to
, to-
najbardziej prawdopodobną wartością
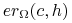 jest
jest 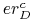 ,
, -
z prawdopodobieństwem
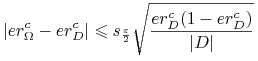
-
1.1.1.2. Systemy informacyjne i tablice decyzyjne
-
Teoria zbiorów przybliżonych została wprowadzona w latach 80-tych przez prof. Zdzisława Pawlaka.
-
Głównym celem jest dostarczanie narzędzi dla problemu aproksymacji pojęć (zbiorów).
-
Zastosowania w systemach decyzyjnych:
-
Redukcja danych, selekcja ważnych atrybutów
-
Generowanie reguł decyzyjnych
-
Odkrywanie wzorców z danych: szablony, reguły asocjacyjne
-
Odkrywanie zależności w danych
-
Przykład
| Pacjent | Wiek | Płeć | Chol. | ECG | Rytm serca | Chory? |
|---|---|---|---|---|---|---|
| 53 | M | 203 | hyp | 155 | Tak | |
| 60 | M | 185 | hyp | 155 | Tak | |
| 40 | M | 199 | norm | 178 | Nie | |
| 46 | K | 243 | norm | 144 | Nie | |
| 62 | F | 294 | norm | 162 | Nie | |
| 43 | M | 177 | hyp | 120 | Tak | |
| 76 | K | 197 | abnorm | 116 | Nie | |
| 62 | M | 267 | norm | 99 | Tak | |
| 57 | M | 274 | norm | 88 | Tak | |
| 72 | M | 200 | abnorm | 100 | Nie |
Tablica decyzyjna
Jest to struktura ![]() , gdzie
, gdzie
-
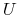 jest zbiorem obiektów:
jest zbiorem obiektów: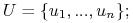
-
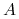 jest zbiorem atrybutów postaci
jest zbiorem atrybutów postaci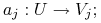
-
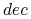 jest specjalnym atrybutem zwanym decyzją
jest specjalnym atrybutem zwanym decyzją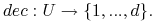
Tablica decyzyjna powstaje ze zwykłych tablic danych poprzez sprecyzowanie:
-
Atrybutów (nazwanych warunkowymi): cechy, których wartości na obiektach są dostępne, np. pomiary, parametry, dane osobowe, …
-
Decyzji (atrybut decyzyjny):, t.j. cecha “ukryta” związana z pewną znaną częściowo wiedzą o pewnym pojęciu:
-
Decyzja jest znana tylko dla obiektów z (treningowej) tablicy decyzyjnej;
-
Jest podana przez eksperta (np. lekarza) lub na podstawie późniejszych obserwacji (np. ocena giełdy);
-
Chcemy podać metodę jej wyznaczania dla dowolnych obiektów na podstawie wartości atrybutów warunkowych na tych obiektach.
-
4.5cm Przedstawiona tablica decyzyjna zawiera:
-
8 obiektów będących opisami pacjentów
-
3 atrybuty: Headache Muscle pain, Temp.
-
Decyzję stwierdzącą czy pacjent jest przeziębiony czy też nie. lub nie
8cm\example
![]()
Ból głowy
Ból mięśni
Temp.
Grypa
p1
Tak
Tak
N
Nie
p2
Tak
Tak
H
Tak
p3
Tak
Tak
VH
Tak
p4
Nie
Tak
N
Nie
p5
Nie
Nie
H
Nie
p6
Nie
Tak
VH
Tak
p7
Nie
Tak
H
Tak
p8
Nie
Nie
VH
Nie
Dane są obiekty ![]() i zbiór atrybutów
i zbiór atrybutów ![]() ,
mówimy, że
,
mówimy, że
-
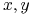 są rozróżnialne przez
są rozróżnialne przez  wtw, gdy istnieje
wtw, gdy istnieje 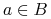 taki, że
taki, że 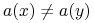 ;
; -
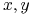 są nierozróżnialne przez
są nierozróżnialne przez  , jeśli one są
identyczne na
, jeśli one są
identyczne na  , tzn.
, tzn. 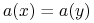 dla każdego
dla każdego 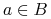 ;
; -
![[x]_{B}](wyklady/syd/mi/mi88.png) = zbiór obiektów nierozróżnialnych z
= zbiór obiektów nierozróżnialnych z 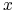 przez
przez  .
.
-
Dla każdych obiektów
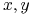 :
:-
albo
![[x]_{B}=[y]_{B}](wyklady/syd/mi/mi5.png) ;
; -
albo
![[x]_{B}\cap[y]_{B}=\emptyset](wyklady/syd/mi/mi50.png) .
.
-
-
Relacja
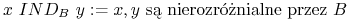
jest relacją równoważności.
-
Każdy zbiór atrybutów
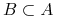 wyznacza podział
zbioru obiektów na klasy nierozróżnialności.
wyznacza podział
zbioru obiektów na klasy nierozróżnialności.
Dla ![]()
4.5cm
-
obiekty
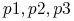 są nierozróżnialne;
są nierozróżnialne; -
są 3 klasy nierozróżnialności relacji
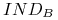 :
: -
8cm\example
![]()
Ból głowy
Ból mięśni
Temp.
Grypa
p1
Tak
Tak
N
Nie
p2
Tak
Tak
H
Tak
p3
Tak
Tak
VH
Tak
p4
Nie
Tak
N
Nie
p5
Nie
Nie
H
Nie
p6
Nie
Tak
VH
Tak
p7
Nie
Tak
H
Tak
p8
Nie
Nie
VH
Nie
1.1.1.3. Aproksymacja pojęć

<2> Aproksymacja funkcji \block
-
Sztuczna sieć neuronowa;
-
Twierdzenie Kolmogorowa;
-
Modele sieci.
 \block
\block
Aproksymacja pojęć
-
Uczenie indukcyjne;
-
COLT;
-
Metody uczenia się.
Wnioskowanie aproksymacyjne
-
Wnioskowanie rozmyte;
-
Wnioskowanie Boolowskie, teoria zbiorów przybliżonych;
-
Inne: wnioskowanie Bayesowskie, sieci przekonań, …
-
Klasyfikatory (algorytmy klasyfikujące) i metody oceny klasyfikatorów
-
Metody rozumowania Boolowskiego
-
Teoria zbiorów przybliżonych
-
Reguły decyzyjne, drzewo decyzyjne i lasy decyzyjne
-
Klasyfikatory Bayesowskie
-
Sieci neuronowe
-
COLT: Obliczeniowa Teoria Uczenia się
-
Metody przygotowywania danych
-
SVM: Maszyna wektorów podpierających
-
Metody wzmacniania klasyfikatorów (ang. Boosting)
1.1.1.4. Nie ma nic za darmo czyli “Non Free Lunch Theorem”
-
Znaleźć optimum nieznanej funkcji
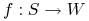 (
(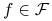 ), gdzie
), gdzie 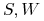 są skończonymi zbiorami.
są skończonymi zbiorami. -
Działanie algorytmu przeszukiwania
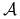 dla funkcji
dla funkcji 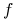 jest identyfikowane z wektorem:
jest identyfikowane z wektorem: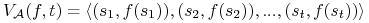
-
Ocena algorytmu:
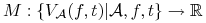 . Np.
. Np.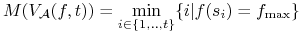
-
Warunek NFL: Dla dowolnej funkcji
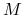 , i dla dowolnych algorytmów
, i dla dowolnych algorytmów 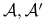
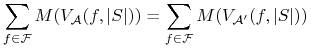
-
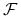 jest zamknięta względem permutacji: dla dowolnej funkcji
jest zamknięta względem permutacji: dla dowolnej funkcji 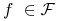 i
dowolnej permutacji
i
dowolnej permutacji 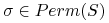 mamy
mamy 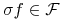
Twierdzenie o NFL
-
Zachodzi równoważność
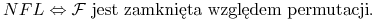
-
Prawdopodobieństwo wylosowania niepustej klasy funkcji zamkniętej wzg. permutacji wynosi:
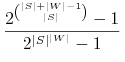
-
Algorytm
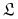 dobrze się uczy pojęcia
dobrze się uczy pojęcia 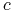 jeśli
jeśli 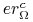 jest mały.
jest mały. -
Niech
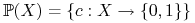 .
.Czy można stwierdzić wiedzieć, że algorytm
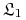 wyuczy się wszystkich pojęć z
wyuczy się wszystkich pojęć z
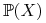 lepiej niż algorytm
lepiej niż algorytm 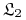 ?
? -
”No Free Lunch theorem” (Wolpert, Schaffer) w wersji problemów uczenia się głosi, że:
-
Żaden algorytm nie może być najlepszy w wyuczeniu wszystkich pojęć.
-
Każdy algorytm jest najlepszy dla takiej samej liczby pojęć
-
Ale interesuje nas tylko pewna klasa problemów czyli klasa pojęć
-
Wniosek: Należy znaleźć odpowiedni algorytm do każdego problemu.
-
1.1.2. Sprawy organizacyjne
-
Obecność: 20%
-
Projekt: 40%
-
Egzamin: 40%




