Zagadnienia
10. SVM: Maszyny wektorów podpieraja̧cych
10.1. SVM: Maszyny wektorów podpieraja̧cych
10.1.1. Wprowadzenie
Dana jest próbka treningowa
0.5
0.58
\column
-
Klasyfikatorem liniowym nazywamy funkcję
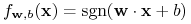
-
Próbka
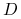 jest liniowo seperowana jeśli istnieje
klasyfikator liniowy
jest liniowo seperowana jeśli istnieje
klasyfikator liniowy 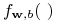 taki, że
taki, że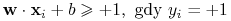
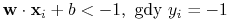
0.5
0.5
\column
-
Uproszczony warunek:
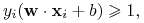
dla każdego
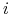 .
. -
Każda z tych linii dobrze seperuje punkty;
-
Która z nich jest najlepsza?
-
Margines = szerokość bezpiecznego obszaru po obu stronach hiperpłaszczyzny;
-
Margines jest wyznaczony przez 2 hiperpłaszczyzny.
-
Chcemy znaleźć klasyfikator z maksymalnym marginesem
0.5
-
Niech
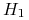 ,
, 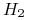 będą brzegami marginesu;
będą brzegami marginesu; -
Powiniśmy oprzeć brzegi o punkty z próbki treningowej
-
Te punkty nazywamy wektorami podpierającymi
-
Równanie
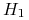 i
i 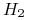 :
: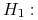
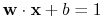
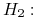
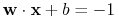
0.5
Odległość między ![]() a
a ![]() :
:
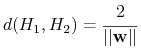 |
Maksymalizujemy ![]() lub minimalizujemy
lub minimalizujemy ![]() .
.
Zadanie LSVM
Znaleźć ![]() i
i ![]() które minimalizują
które minimalizują
przy ograniczeniach
Q: Jak rozwiązać tego typu zagadnienia?
A: Metodą gradientu?, symulowanego wyżrzania?, odwracanie macierzy? EM? Newton? PROGRAMOWANIE KWADRATOWE?
-
Znaleźć
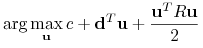
-
przy założeniach:
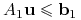
-
oraz
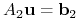
To zagadnienie jest dobrze zbadane i istnieją bardzo efektywne algorytmy rozwiązujące ten problem
-
Rozwiązywanie zagadnienia LSVM
 znalezienie punktu
siodłowego wielomianu Lagrange'a:
znalezienie punktu
siodłowego wielomianu Lagrange'a:
![L(\mathbf{w},b,\alpha)=\frac{1}{2}(\mathbf{w}\cdot\mathbf{w})-\sum _{{i=1}}^{n}\alpha _{i}\left\{[(\mathbf{x}_{i}\cdot\mathbf{w})-b]y_{i}-1\right\}](wyklady/syd/mi/mi769.png)
gdzie
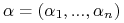 jest wektorem nieujemnych współczynników Lagrange'a
jest wektorem nieujemnych współczynników Lagrange'a -
Punkt siodłowy = maksimum funkcji względem
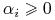 i minimum funkcji względem
i minimum funkcji względem 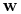 i
i 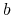 .
.
Twierdzenie Karusha-Kuhna-Tuckera: warunkiem koniecznym istnienia punktu siodlowego jest
-
zerowanie się gradientu wzg.
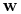 , czyli
, czyli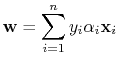
(10.1) -
zerowanie się pochodnej wzg.
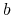 , czyli
, czyli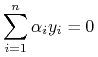
(10.2) -
spełnienie warunku:
![\alpha _{i}\left\{[(\mathbf{x}_{i}\cdot\mathbf{w}_{0})-b_{0}]y_{i}-1\right\}=0,\text{ for }i=1,...,n](wyklady/syd/mi/mi767.png)
(10.3)
Po uwzględnieniu tych warunków (na istnienie punktu siodłowego) mamy nowy problem optymalizacyjny:
-
Znaleźć wektor
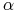 będący maksimum funkcji
będący maksimum funkcji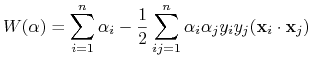
(10.4) -
przy ograniczeniach
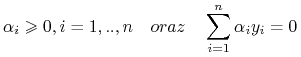
(10.5)
Niech wektor ![]() będzie rozwiązaniem
maksymalizującym (4) przy ograniczeniach (5).
będzie rozwiązaniem
maksymalizującym (4) przy ograniczeniach (5).
-
Z (3) wynika, że jeśli
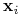 nie jest wektorem podpierającym to
nie jest wektorem podpierającym to 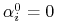 ;
; -
Równania (4) i (5) odbywają się faktycznie tylko po wektorach podpierających.
-
Hyperpłaszczyzna rozdzielająca ma postać
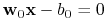 gdzie
gdzie![\mathbf{w}_{0}=\sum _{{\text{wektory podp.}}}y_{i}\alpha _{i}^{0}\mathbf{x}_{i}\quad b_{0}=\frac{1}{2}[(\mathbf{w}_{0}\cdot\mathbf{x}^{{(1)}})+(\mathbf{w}_{0}\cdot\mathbf{x}^{{(-1)}})]](wyklady/syd/mi/mi827.png)
tu
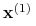 i
i 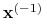 są dowolnymi
wektorami podpierającymi z każdej z klas.
są dowolnymi
wektorami podpierającymi z każdej z klas.
Ostateczna funkcja decyzyjna:
| (10.6) |
10.1.2. Brak liniowej separowalności danych
10.1.2.1. Nieznaczna nieseparowalność
-
Założenie o separowalności klas jest nienaturalna;
-
Modyfikacja:
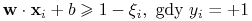
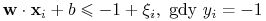
gdzie stałe
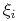 spełniają warunki:
spełniają warunki: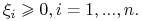
-
Zmodyfikowana funkcja do minimalizacji
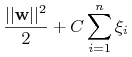
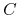 jest stałą “karą” za niespełnienie idealnych warunków.
jest stałą “karą” za niespełnienie idealnych warunków.
Ogólne zadanie SVM
Znaleźć ![]() i
i ![]() które minimalizują
które minimalizują
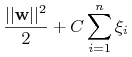 |
przy ograniczeniach
Można pokazać, że zarówno i w tym przypadku, możemy sprowadzić do problemu
-
Znaleźć wektor
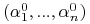 będący maksimum funkcji
będący maksimum funkcji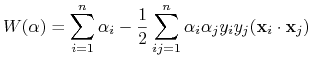
(10.7) -
przy ograniczeniach
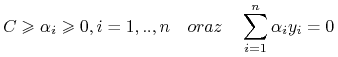
(10.8)
A następnie stosować funkcję decyzyjną: \block
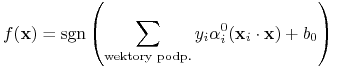 |
(10.9) |
10.1.2.2. Zmiana przetrzeni atrybutów
-
Przekształcimy dane do bogatszej przetrzeni cech:
-
Wystarczy zamienić iloczyny skalarne
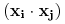 we wszystkich wzorach
na
we wszystkich wzorach
na 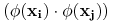
-
PROBLEM OBLICZENIOWY: czas wykonania iloczynu skalarnego
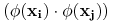 wynosi
wynosi 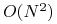
-
TRIK: Kernel functions
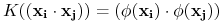
-
Zmieniona funkcja:
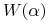
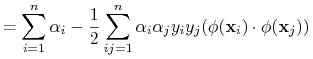
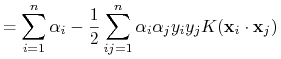
10.1.3. Implementacja
\blockProblem
- Wejście:
-
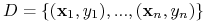 ;
;
 : funkcja jądrowa.
: funkcja jądrowa. - Wyjście:
-
wektor
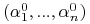 będący maksimum funkcji
będący maksimum funkcji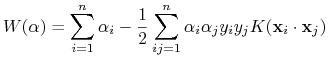
przy ograniczeniach
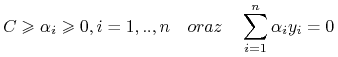
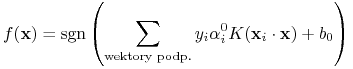 |




