2. Problem klasyfikacji i klasyfikatory

2.1. Problem klasyfikacji i klasyfikatory

Założenie: Dany jest skończony zbiór obiektów 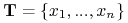$\mathbf{T}=\{ x_{1},...,x_{n}\}$ . Ten zbiór nazywamy zbiorem treningowym
- Każdy obiekt (rekord) jest opisany wektorem informacyjnym, składającym się z wartości pochodzących z dziedziny pewnych atrybutów warunkowych.
- Wyróżniony jest jeden atrybut, zwany też atrybutem decyzyjnym
  
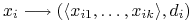
  $x_{i}\longrightarrow(\langle x_{{i1}},\ldots,x_{{ik}}\rangle,d_{i})$
Cel: wyznaczyć klasę decyzyjną, do której należy nowy nieznany dotąd obiekt.
Jak? Znaleźć zależność (najlepiej funkcyjną) między atrybutem decyzyjnym a atrybutami warunkowymi.

Tworzenie modelu: opisywanie klas decyzyjnych
- Klasa decyzyjna = zbiór obiektów mających taką samą wartość na atrybucie decyzyjnym
- Klasyfikator: algorytm określenia klasy decyzyjnej obiektów za pomocą ich wartości na atrybutach warunkowych.
- Klasyfikatory mogą być opisane za pomocą formuł logicznych, drzew decyzyjnych lub formuł matematycznych.
Korzystanie z modelu do przypisanie nowym nieznanym obiektom ich klasy decyzyjne.

Problem: Jak oceniać model?

Wiele problemów decyzyjnych można opisać jako problem klasyfikacji
DSS (Decision Support System) jest systemem komputerowym dostarczającym narzędzia do rozwiązywania problemów klasyfikacji.

Wejście:

Zbiór treningowy

Wyjście:

Klasyfikator(y)
Wymagania:
- Szybkość podejmowania decyzji, skalowalność
- Skuteczność
- Racjonalność
- Możliwość współpracy z ekspertem: doradztwo, adaptacja, negocjacja, adopcja wiedzy eksperskiej, …

Są to metody leniwej klasyfikacji, które opóźniają proces przetwarzania danych aż do momentu kiedy pojawi się nowy obiekt do klasyfikowania
Typowe metody:
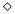- $\diamond$ k-nearest neighbor approach
  - $*$ Przykłady treningowe są przedstawione jako punkty w metrycznej przestrzeni.
- $\diamond$ Locally weighted regression
  - $*$ Konstruuje lokalne aproksymacje pojęć
- $\diamond$ Case-based reasoning
  - $*$ Korzysta z symbolicznych reprezentacji i metod wnioskowania w oparciu o bazę wiedzy

\block

algorytm najbliższych sąsiadów

Input:: Tablica decyzyjna 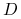$D$ , nowy obiekt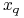 $x_{q}$
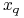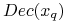Output:: Klasa decyzyjna, do której należy $x_{q}$ (czyli $Dec(x_{q})$ )
Krok 1:: Szukaj w zbiorze 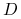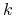$D$ , $k$ najbliżej położonych obiektów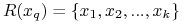 $R(x_{q})=\{ x_{1},x_{2},...,x_{k}\}$
Krok 2:: Wyznacz klasę dla 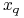$x_{q}$ na podstawie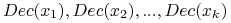 $Dec(x_{1}),Dec(x_{2}),...,Dec(x_{k})$

\columns\column

0.4 0.59 \column

Najczęściej wykorzystany dla danych z atrybutami numerycznymi
Wymagania:
- Zbiór treningowy
- Funkcja odległości między obiektami
- Wartość parametru 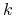$k$ , liczba rozpatrywanych sąsiadów
Podczas klasyfikacji:
- Wyznaczanie k najbliższych sąsiadów
- Wyznaczenie klasy decyzyjnej nowego obiektu na podstawie klas decyzyjnych najbliższych sąsiadów (np. przez głosowanie).

Jest to przykład metody leniwej, gdyż
- Nie buduje jawnego modelu wiedzy
- Proces klasyfikacji może być czasochłonny
Jeśli k jest za mała, klasyfikator będzie wrażliwa na drobne szumy w danych
Jeśli k jest zbyt duża:
- Wysoka złożoność obliczeniowa
- Otoczenia mogą zawierać obiekty z innych klas
Algorytm k-NN dla ciągłej decyzji
- Wystarczy obliczyć średnią z decyzji najbliższych sąsiadów

Problem skalowania atrybutów
- Np. opis człowieka:
  - (Wzrost [m], Waga [kg], Klasa)
  - Wzrost odchyla się od 1.5 m do 1.85 m
  - Waga może mieć wartość od 45 kg do 120 kg
  Odległość euklidesowa jest bardziej wrażliwa na różnicę wag niż różnicę wzrostu.
Przekleństwo wymiarów
Może produkować wyniki niezgodne z intuicją (np. klasyfikacji dokumentów)
- Rozwiązanie: Normalizacja
Sąsiedzi ważeni względem odległośc
- Wpływ sąsiada 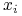$x_{i}$ na obiekt testowy 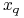$x_{q}$ jest ważony przez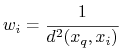 $w_{i}=\cfrac{1}{d^{2}(x_{q},x_{i})}$
- Bliżsi sąsiedzi mają większy wpływ

\columns\column

0.6

Dany jest zbiór treningowy 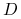$D$ , prawdopodobieństwo posteriori hipotezy 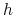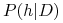$h$ – $P(h|D)$ – można liczyć wzorem Bayesa.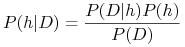

$P(h|D)=\frac{P(D|h)P(h)}{P(D)}$
MAP (maximum posteriori) hypothesis

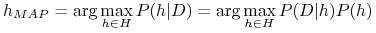
$h_{{MAP}}=\arg\max _{{h\in H}}P(h|D)=\arg\max _{{h\in H}}P(D|h)P(h)$
Trudności: ta metoda wymaga znajomości wielu rozkładów prawdopodobieństw $\implies$ wysoki koszt obliczeniowy

\column

0.39

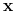
Klasyfikacja obiektu opisanego przez $\mathbf{x}$

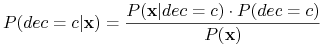
$P(dec=c|{\mathbf{x}})=\frac{P({\mathbf{x}}|dec=c)\cdot P(dec=c)}{P({\mathbf{x}})}$
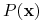$P({\mathbf{x}})$ jest wspólna dla wszystkich hipotez;
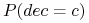$P(dec=c)$ – częstość występowania klasy $c$ ;
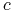Znaleźć 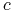$c$ tak, że 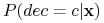$P(dec=c|{\mathbf{x}})$ było maksymalne, czyli, aby 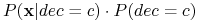$P({\mathbf{x}}|dec=c)\cdot P(dec=c)$ było maksymalne;
Problem: obliczenie 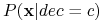$P({\mathbf{x}}|dec=c)$ jest czasochłonne!

Naiwne założenie: atrybuty są warunkowo niezależne!

Wówczas

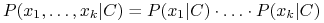
$P(x_{1},\ldots,x_{k}|C)=P(x_{1}|C)\cdot\ldots\cdot P(x_{k}|C)$
Czyli

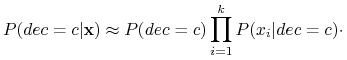
$P(dec=c|{\mathbf{x}})\approx P(dec=c)\prod _{{i=1}}^{k}P(x_{i}|dec=c)\cdot$

To założenie znacznie obniża złożoność obliczeniowy.

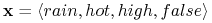
Nowy obiekt ${\bf x}=\langle rain,hot,high,false\rangle$

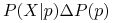
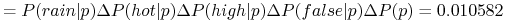
$\displaystyle P(X|p)·P(p)$ $\displaystyle=P(rain|p)·P(hot|p)·P(high|p)·P(false|p)·P(p)=0.010582$

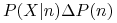
$\displaystyle P(X|n)·P(n)$ $\displaystyle=P(rain|n)·P(hot|n)·P(high|n)·P(false|n)·P(n)=0.018286$
X jest klasyfikowany do klasy n (don’t play)

Założenie o niezależności:
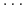- $\ldots$ powoduje, że obliczenia staje się możliwe
- $\ldots$ optymalny klasyfikator o ile ono jest prawdziwe
- $\ldots$ ale warunek bardzo rzadko spełniony w praktyce (atrybuty są często korelowane).
Próby pokonania te ograniczenia:
- Sieci Bayesowskie, które łączą metody wnioskowania Bayesowskiego z zależnościami między atrybutami
- Drzewa decyzyjne, które przeprowadzają dedukcyjne kroki na pojedyńczych atrybutach, począwszy od najważniejszego

Sieci Bayesowskie dopuszczają “warunkową niezależność” podzbiorów zmiennych.
Jest to graficzny model zależności przyczynowo-skutkowych
Naive Bayes jest szczególnym przypadkiem sieci Bayesowskiej (jakim?)
Problemy związane uczeniem sieci Bayesowskich:
- Prypadek najłatwiejszy: zarówno struktura sieci, jak i wszystkie zmienne są znane.
- Znana jest struktura, ale brakuje rozkładów zmiennych.
- Nawet struktura sieci nie jest z góry zadana.

\block

Ogólna formuła

$P(x_{1},\ldots,x_{k}|C)=\prod _{{i=1}}^{k}P(x_{i}|parent(x_{i}),C)$

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

	$\displaystyle P(X\|p)·P(p)$	$\displaystyle=P(rain\|p)·P(hot\|p)·P(high\|p)·P(false\|p)·P(p)=0.010582$
	$\displaystyle P(X\|n)·P(n)$	$\displaystyle=P(rain\|n)·P(hot\|n)·P(high\|n)·P(false\|n)·P(n)=0.018286$