Zagadnienia
6. Metoda drzew decyzyjnych
6.1. Metoda drzew decyzyjnych
6.1.1. Wprowadzenie
6.1.1.1. Definicje
-
Jest to struktura drzewiasta, w której
-
węzły wewnętrzne zawierają testy na wartościach atrybutów
-
z każdego węzła wewnętrznego wychodzi tyle gałęzi, ile jest możliwych wyników testu w tym węzle;
-
liście zawierają decyzje o klasyfikacji obiektów
-
-
Drzewo decyzyjne koduje program zawierający same instrukcje warunkowe
6.1.1.2. Funkcje testu
| x | outlook | Temperature | humidity | wind | play(x) |
|---|---|---|---|---|---|
| 1 | sunny | hot | high | weak | no |
| 2 | sunny | hot | high | strong | no |
| 3 | overcast | hot | high | weak | yes |
| 4 | rain | mild | high | weak | yes |
| 5 | rain | cold | normal | weak | yes |
| 6 | rain | cold | normal | strong | no |
| 7 | overcast | cold | normal | strong | yes |
| 8 | sunny | mild | high | weak | no |
| 9 | sunny | cold | normal | weak | yes |
| 10 | rain | mild | normal | weak | yes |
| 11 | sunny | mild | normal | strong | yes |
| 12 | overcast | mild | high | strong | yes |
| 13 | overcast | hot | normal | weak | yes |
| 14 | rain | mild | high | strong | no |
Wyróżniamy 2 klasy funkcji testów
-
Testy operują na wartościach pojedyńczego atrybutu (ang. univariate tree):
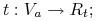
-
Testy będące kombinacją wartości kilku atrybutów (ang. multivariate tree):
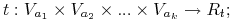
gdzie
-
Va : dziedzina atrybutu
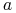 ;
; -
Rt : zbiór możliwych wyników testu;
-
Dla atrybutów nominalnych
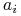 oraz obiektu
oraz obiektu 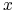 :
:-
test tożsamościowy:
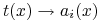
-
test równościowy:
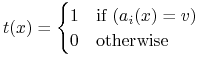
-
test przynależnościowy:
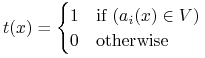
-
-
Dla atrybutów o wartościach ciągłych:
-
test nierównościowy:
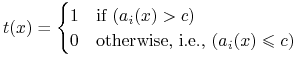 gdzie
gdzie 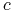 jest wartością progową lub cięciem
jest wartością progową lub cięciem
-
6.1.1.3. Optymalne drzewo
-
Jakość drzewa ocenia się
-
za pomocą rozmiaru: im drzewo jest mniejsze, tym lepsze
-
mała liczba węzłów,
-
mała wysokość, lub
-
mała liczba liści;
-
-
za pomocą dokładności klasyfikacji na zbiorze treningowym
-
za pomocą dokładności klasyfikacji na zbiorze testowym
-
-
Na przykład:
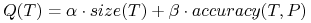
gdzie
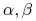 są liczbami rzeczywistymi
są liczbami rzeczywistymisize(.) jest rozmiarem drzewa
accuracy(.,.) jest jakością klasyfikacji
Problem konstrukcji drzew optymalnych: Dane są:
-
tablica decyzyjna
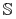
-
zbiór funkcji testów
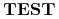 ,
, -
kryterium jakości
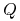
Szukane: drzewo decyzyjne ![]() o najwyższej jakości
o najwyższej jakości ![]() .
.
-
Dla większości parametrów, problem szukania optymalnego drzewa jest NP-trudny !
-
Wnioski:
Trudno znaleźć optymalne drzewo w czasie wielomianowym;
Konieczność projektowania heurystyk.
-
Quiz: Czy drzewo z przykładu jest optymalne?
6.1.2. Konstrukcja drzew decyzyjnych
-
Kryterium stopu: Zatrzymamy konstrukcji drzewa, gdy aktualny zbiór obiektów:
-
jest pusty lub
-
zawiera obiekty wyłącznie jednej klasy decyzyjnej lub
-
nie ulega podziale przez żaden test
-
-
Wyznaczenie etykiety zasadą większościową:
![kategoria(P,dec)=\arg\max _{{c\in V_{{dec}}}}|P_{{[dec=c]}}|](wyklady/syd/mi/mi486.png)
tzn., etykietą dla danego zbioru obiektów jest klasa decyzyjna najliczniej reprezentowana w tym zbiorze.
-
Kryterium wyboru testu: heurytyczna funkcja oceniająca testy.
6.1.2.1. Kryterium wyboru testu
Każdy zbiór obiektów ![]() ulega podziałowi na klasy decyzyjne:
ulega podziałowi na klasy decyzyjne:
gdzie ![]() .
.
Wektor ![]() , gdzie
, gdzie ![]() , nazywamy
rozkładem klas decyzyjnych w
, nazywamy
rozkładem klas decyzyjnych w ![]() .
.
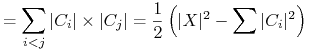 |
|||
Funkcja ![]() oraz
oraz ![]() przyjmują
przyjmują
-
największą wartość, gdy rozkład klas decyzyjnych w zbiorze
 jest równomierny.
jest równomierny. -
najmniejszą wartość, gdy wszystkie obiekty w
 są jednej kategorii
(
są jednej kategorii
( jest jednorodny)
jest jednorodny)
W przypadku 2 klas decyzyjnych:
Niech ![]() definiuje podział
definiuje podział ![]() na podzbiory:
na podzbiory: ![]() . Możemy
stosować następujące miary do oceniania testów:
. Możemy
stosować następujące miary do oceniania testów:
-
liczba par obiektów rozróżnionych przez test t.
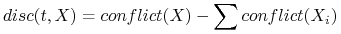
-
kryterium przyrostu informacji (ang. Inf. gain).
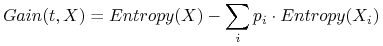
Im większe są wartości tych ocen, tym lepszy jest test.
-
Monotoniczność: Jeśli
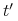 definiuje drobniejszy podział niż
definiuje drobniejszy podział niż 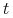 to
to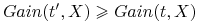
(analogiczną sytuację mamy dla miary
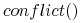 .
. -
Funkcje ocen testu
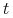 przyjmują małe wartości
jeśli rozkłady decyzyjne w podzbiorach wyznaczanych przez
przyjmują małe wartości
jeśli rozkłady decyzyjne w podzbiorach wyznaczanych przez 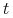 są zbliżone.
są zbliżone.
Zamiast bezwzględnego przyrostu informacji, stosujemy współczynnik przyrostu informacji
gdzie ![]() , zwana wartością informacyjną testu
, zwana wartością informacyjną testu ![]() (information value), jest definiowana jak nast.:
(information value), jest definiowana jak nast.:
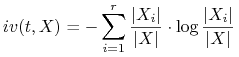 |
Ocena funkcji testu
-
Rozróżnialność:
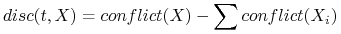
-
Przyrostu informacji (Information gain).
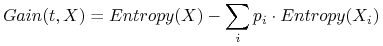
-
Współczynnik przyrostu informacji (gain ratio)
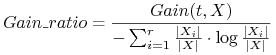
-
Inne (np. Gini's index, test
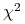 , …)
, …)
6.1.2.2. Przycinanie drzew
-
Problem nadmiernego dopasowania do danych trenujących (prob. przeuczenia się).
-
Rozwiązanie:
-
zasada najkrótszego opisu: skracamy opis kosztem dokładności klasyfikacji w zbiorze treningowym
-
zastąpienie podrzewa nowym liściem (przycinanie) lub mniejszym podrzewem.
-
-
Podstawowe pytania:
-
Q: Kiedy poddrzewo może być zastąpione liściem?
-
A: Jeśli nowy liść jest niegorszy niż istniejące poddrzewo dla nowych obiektów (nienależących do zbioru treningowego).
-
Q: Jak to sprawdzić?
-
A: Testujemy na próbce zwanej “zbiorem przycinania”!
-
-
Niech
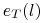 - błąd klasyfikacji kandydującego liścia l,
- błąd klasyfikacji kandydującego liścia l,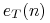 - błąd klasyfikacji poddrzewa o korzeniu w
- błąd klasyfikacji poddrzewa o korzeniu w 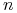 .
. -
Przycinanie ma miejsce, gdy
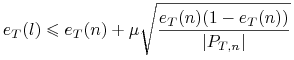
na ogół przyjmujemy
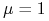 .
.
6.1.2.3. Problem brakujących wartości (ang. null-values)
Możliwe są następujące rozwiązania:
-
Zredukowanie wartości kryterium wyboru testu (np. przyrostu informacji) dla danego testu o współczynnik równy:
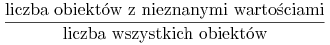
-
Wypełnienie nieznanych wartości atrybutu najczęściej występującą wartością w zbiorze obiektów związanych z aktualnym węzłem
-
Wypełnienie nieznanych wartości atrybutu średnią ważoną wyznaczoną na jego zbiorze wartości.
Możliwe rozwiązania:
-
Zatrzymanie procesu klasyfikacji w aktualnym węźle i zwrócenie większościowej etykiety dla tego węzła (etykiety, jaką ma największą liczbę obiektów trenujących w tym węźle)
-
Wypełnienie nieznanej wartości według jednej z heurystyk podanych wyżej dla przypadku konstruowania drzewa
-
Uwzględnienie wszystkich gałęzi (wszystkich możliwych wyników testu) i połączenie odpowiednio zważonych probabilistycznie rezultatatów w rozkład prawdopodobieństwa na zbiorze możliwych klas decyzyjnych dla obiektu testowego.




