Zagadnienia
7. Problem dyskretyzacji
7.1. Problem dyskretyzacji
7.1.1. Przypomnienia podstawowych pojęć
Tablicą decyzyjną nazywamy strukturę
![]() gdzie
gdzie
![]() nazywa się zbiorem obiektów
nazywa się zbiorem obiektów
![]() jest zbiorem atrybutów postaci
jest zbiorem atrybutów postaci
![]() jest specjalnym atrybutem zwanym decyzją
jest specjalnym atrybutem zwanym decyzją
| … | ||||
| 100 | 27 | … | 1 | |
| 120 | 86 | … | 1 | |
| 70 | 52 | … | 1 | |
| 95 | 18 | … | 1 | |
| … | … | … | … | |
| 71 | 82 | … | 2 | |
| … | … | … | … | |
-
Klasy decyzyjne:
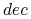 definiuje podział
definiuje podział 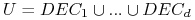 gdzie
gdzie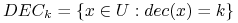
-
Rozróżnialność: Dane są obiekty
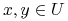 zbiór atrybutów
zbiór atrybutów 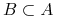 , mówimy, że
, mówimy, że 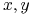 są rozróżnialne przez
są rozróżnialne przez  wtw, gdy istnieje
wtw, gdy istnieje 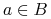 taki, że
taki, że
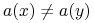
Zbiór atrybutów ![]() nazywamy reduktem tablicy
nazywamy reduktem tablicy
![]() wtw, gdy
wtw, gdy
-
dla dowolnych obiektów
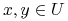
jeśli
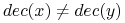 i
i 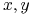 są rozróżnialne przez
są rozróżnialne przez 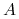 ,
,to są również rozróżnialne przez

(
 zachowuje rozróżnialność zbioru
zachowuje rozróżnialność zbioru 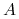 )
)
-
 jest niezredukowalny (tzn. żaden właściwy podzbiór
jest niezredukowalny (tzn. żaden właściwy podzbiór  nie zachowuje rozróżnialności zbioru
nie zachowuje rozróżnialności zbioru 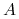 )
)
Problemy:
-
Czy istnieje redukt zawierający
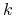 atrybutów?
atrybutów? -
Znaleźć redukt o najmniejszej liczbie atrybutów.
-
funkcje
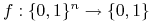 nazywamy Boolowskimi.
nazywamy Boolowskimi. -
monotoniczne funkcje Boolowskie można zapisać bez użycia negacji.
-
jednomian
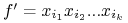 nazywamy
implikantem pierwszym funkcji monotonicznej
nazywamy
implikantem pierwszym funkcji monotonicznej 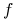 jeśli
jeśli-
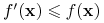 dla każdego wektora
dla każdego wektora 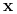 (jest implikantem)
(jest implikantem) -
każda funkcja większa od
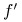 nie jest implikantem
nie jest implikantem
-
-
Np. funkcja
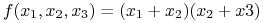
posiada 2 implikanty pierwsze:
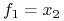 i
i 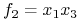
7.1.2. Problem dyskretyzacji
Dana jest niesprzeczna tablica decyzyjna ![]()
-
Mówimy, że cięcie
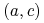 rozróżnia obiekty
rozróżnia obiekty 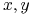 jeśli albo
jeśli albo 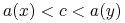 lub
lub 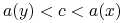 .
. -
Zbiór cięć
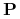 nazywamy niesprzecznym z
nazywamy niesprzecznym z 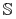 jeśli dla
każdej pary obiektów
jeśli dla
każdej pary obiektów 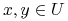 takich, że
takich, że 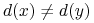 istnieje cięcie
istnieje cięcie
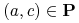 rozróżniające
rozróżniające 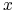 i
i 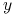 .
. -
Zbiór cięć
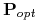 nazywamy optymalnym dla
nazywamy optymalnym dla 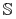 jeśli
jeśli
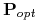 posiada najmniejszą liczbę cięć wśród niesprzecznych zbiorów
cięć.
posiada najmniejszą liczbę cięć wśród niesprzecznych zbiorów
cięć.
7.1.2.1. Istniejące metody dyskretyzacji
-
Lokalne a globalne metody:
-
Statyczne a dynamiczne metody: Metody statyczne poszukują zbioru cięć dla każdego atrybutu w sposób niezależny od innych atrybutów. Metody dynamiczne szukają cięć na wszystkich atrybutach jednocześnie
-
Z nadzorem lub bez:
-
<+-|alert@+> Podział na przedziały o równych długościach lub równych częstotliwościach;
-
<+-|alert@+> Metoda OneR
-
<+-|alert@+> Testy statystyczne
-
<+-|alert@+> Z użyciem funkcji entropii;
-
<+-|alert@+> Gini's index
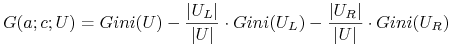
-
Metoda statyczna bez nadzoru: podział danych numerycznych na równomierne przedziały;
-
Rozpatrujemy liczbę różnych najbardziej znaczących cyfr w danym przedziale:
-
jeśli ta liczba wynosi 3,6,7 lub 9 to podziel dany przedział na 3 równe przedziały.
-
jeśli ta liczba wynosi 2,4 lub 8 to podziel dany przedział na 4 równe przedziały.
-
jeśli ta liczba wynosi 1,5 lub 10 to podziel dany przedział na 5 równych przedziałów.
-
7.1.3. Dyskretyzacja metodą wnioskowania Boolowskiego
Dana jest niesprzeczna tablica decyzyjna ![]()
-
Niech
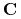 będzie zbiorem kandydujących cięć dla tablicy
będzie zbiorem kandydujących cięć dla tablicy 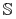 ;
; -
Każde cięcie
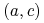 jest skojarzone ze zmienną Boolowską
jest skojarzone ze zmienną Boolowską 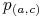 ;
; -
Niech
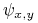 będzie funkcją rozróżnialności dla
będzie funkcją rozróżnialności dla 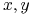 :
: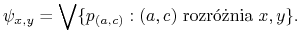
-
Funkcja boolowska
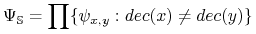
koduje problem dyskretyzacji.
-
Minimalny implikant pierwszy
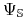
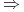 optymalny zbiór
cięć.
optymalny zbiór
cięć.
Ciecia kandydujące
Oznaczmy przez ![]() zmienne
Boolowskie odpowiadające cięciom. Wówczas
zmienne
Boolowskie odpowiadające cięciom. Wówczas
![\begin{array}[]{ll}\psi\left(2,1\right)=p_{1}^{a}+p_{1}^{b}+p_{2}^{b};&\psi\left(2,4\right)=p_{2}^{a}+p_{3}^{a}+p_{1}^{b};\\
\psi\left(2,6\right)=p_{2}^{a}+p_{3}^{a}+p_{4}^{a}+p_{1}^{b}+p_{2}^{b}+p_{3}^{b};&\psi\left(2,7\right)=p_{2}^{a}+p_{1}^{b};\\
\psi\left(3,1\right)=p_{1}^{a}+p_{2}^{a}+p_{3}^{b};&\psi\left(3,4\right)=p_{2}^{a}+p_{2}^{b}+p_{3}^{b};\\
\psi\left(3,6\right)=p_{3}^{a}+p_{4}^{a};&\psi\left(3,7\right)=p_{2}^{b}+p_{3}^{b};\\
\psi\left(5,1\right)=p_{1}^{a}+p_{2}^{a}+p_{3}^{a};&\psi\left(5,4\right)=p_{2}^{b};\\
\psi\left(5,6\right)=p_{4}^{a}+p_{3}^{b};&\psi\left(5,7\right)=p_{3}^{a}+p_{2}^{b}.\end{array}](wyklady/syd/mi/mi535.png) |
Funkcja kodująca problem dyskretyzacji
![\small\begin{array}[]{cl}\Phi _{{\mathbb{S}}}=&\left(p_{1}^{a}+p_{1}^{b}+p_{2}^{b}\right)\left(p_{1}^{a}+p_{2}^{a}+p_{3}^{b}\right)\left(p_{1}^{a}+p_{2}^{a}+p_{3}^{a}\right)\left(p_{2}^{a}+p_{3}^{a}+p_{1}^{b}\right)\\
&p_{2}^{b}\left(p_{2}^{a}+p_{2}^{b}+p_{3}^{b}\right)\left(p_{2}^{a}+p_{3}^{a}+p_{4}^{a}+p_{1}^{b}+p_{2}^{b}+p_{3}^{b}\right)\left(p_{3}^{a}+p_{4}^{a}\right)\\
&\left(p_{4}^{a}+p_{3}^{b}\right)\left(p_{2}^{a}+p_{1}^{b}\right)\left(p_{2}^{b}+p_{3}^{b}\right)\left(p_{3}^{a}+p_{2}^{b}\right).\end{array}](wyklady/syd/mi/mi564.png) |
Po sprowadzeniu do postaci DNF mamy:
Czyli optymalnym zbiorem cięć jest ![]()
-
<+-|alert@+> W algorytmie zachłannym, preferujemy cięcia rozróżniające największą liczbę par obiektów.
-
<+-|alert@+> Miara rozróżnialności dla danego cięcia względem zbioru obiektów
 :
: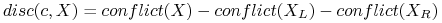
gdzie
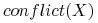 = liczba par obiektów różnych decyzji w zbiorze
= liczba par obiektów różnych decyzji w zbiorze  .
. -
<+-|alert@+> Można realizować zachłanną heurystykę w czasie
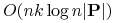 ,
gdzie
,
gdzie 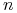 jest liczbą obiektów,
jest liczbą obiektów, 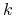 jest liczbą atrybutów,
jest liczbą atrybutów, 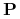 jest zbiorem
cięć znalezionych przez algorytm
jest zbiorem
cięć znalezionych przez algorytm
|
|
||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
7.1.3.1. Uogólnienia problemu dyskretyzacji
-
Hiperpłaszczyzny jako cięcia;
-
Krzywe wyższego rzędu;
-
Grupowanie wartości nominalnych;
-
Inne kryteria optymalizacji.
-
Dyskretyzacja jako proces wstępnego przetwarzania
-
Miarę rozróżnialności można stosować do konstrukcji drzew decyzyjnych.
-
Drzewa generowane tą miarą mają dużo ciekawych własności i dużą skuteczność w procesie klasyfikacji.
-
Rozumowanie Boolowskie jest prostym, ale mocnym narzędziem w dziedzinie rozpoznawania wzorców, eksploracji danych (ang. Data Mining), sztucznej inteligencji …
-
Złożoność funkcji Boolowskiej kodującej dany problem może być miarą trudności tego problemu.




