Zagadnienia
2. Rynek jednookresowy dwustanowy
2.1. Model rynku jednookresowego dwustanowego
Zaczniemy od odpowiedzi na postawione w rozdziale I pytania o wycenę
i zabezpieczenie na przykładzie najprostszego rynku finansowego.
Jest to rynku jednookresowy dwustanowy. Na tym rynku transakcje
odbywają się w dwu chwilach: ![]() i
i ![]() oraz są możliwe dwa
scenariusze wypadków, zatem przestrzeń zdarzeń elementarnych to
oraz są możliwe dwa
scenariusze wypadków, zatem przestrzeń zdarzeń elementarnych to
![]() . Zwykle umawiamy się, że
. Zwykle umawiamy się, że ![]() oznacza sytuację interpretowaną jako korzystna, zaś
oznacza sytuację interpretowaną jako korzystna, zaś ![]() jako
niekorzystna. Ponadto
jako
niekorzystna. Ponadto ![]() , a prawdopodobieństwo
, a prawdopodobieństwo
![]() (tzw. prawdopodobieństwo rzeczywiste) jest takie, że
(tzw. prawdopodobieństwo rzeczywiste) jest takie, że ![]() ,
, ![]() .
.
Na rynku istnieją dwa papiery wartościowe: jeden ryzykowny (np. akcje) i drugi pozbawiony ryzyka — inwestycja polegająca na włożeniu pieniędzy na rachunek bankowy. Ryzyko rozumiemy tu jako niemożność przewidzenia ceny w przyszłości, zależy ona od zajścia konkretnego scenariusza. Niech:
![]() oznacza cenę papieru ryzykownego (za jedną jednostkę)
w chwili
oznacza cenę papieru ryzykownego (za jedną jednostkę)
w chwili ![]() ,
,
![]() oznacza cenę papieru bez ryzyka (za jedną jednostkę)
w chwili
oznacza cenę papieru bez ryzyka (za jedną jednostkę)
w chwili ![]() ,
,
gdzie ![]() . Zakładamy, że stopa procentowa jest stała
i nieujemna, zatem wynosi
. Zakładamy, że stopa procentowa jest stała
i nieujemna, zatem wynosi ![]() (
(![]() ) w okresie czasu od 0 do
) w okresie czasu od 0 do
![]() , czyli w naszym przypadku mamy
, czyli w naszym przypadku mamy
| (2.1) |
Natomiast
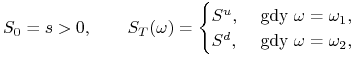 |
(2.2) |
bowiem ![]() przyjmuje dwie wartości, gdyż mamy do czynienia
z dwoma scenariuszami. Możemy bez straty ogólności przyjąć, że
przyjmuje dwie wartości, gdyż mamy do czynienia
z dwoma scenariuszami. Możemy bez straty ogólności przyjąć, że
![]() (dlatego
(dlatego ![]() nazwaliśmy scenariuszem
korzystnym). Cenę
nazwaliśmy scenariuszem
korzystnym). Cenę ![]() możemy zapisać w innej, przydatnej czasami
postaci:
możemy zapisać w innej, przydatnej czasami
postaci:
| (2.3) |
gdzie ![]() wskazuje, o ile procent zmieniła się cena początkowa,
wskazuje, o ile procent zmieniła się cena początkowa,
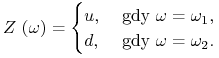 |
2.2. Problem wyceny. Portfel replikujący, arbitraż.
Pierwsza próba wyceny kontraktu związana jest z wykorzystaniem metod matematyki ubezpieczeniowej. Zaprezentujemy ją na przykładzie.
Przykład 2.1
Aktywo ryzykowne kosztuje ![]() w chwili
w chwili ![]() .
Zakładamy, że możliwe (i jednakowo prawdopodobne) są dwa scenariusze
wydarzeń do chwili
.
Zakładamy, że możliwe (i jednakowo prawdopodobne) są dwa scenariusze
wydarzeń do chwili ![]() ; cena aktywa ryzykownego w chwili
; cena aktywa ryzykownego w chwili ![]() może
wynieść
może
wynieść ![]() lub
lub ![]() . Wiemy także,
że cena aktywa bez ryzyka jest równa
. Wiemy także,
że cena aktywa bez ryzyka jest równa ![]() na początku okresu
i
na początku okresu
i ![]() na końcu. Interesuje nas, jak wycenić opcję kupna dającą
wypłatę końcową
na końcu. Interesuje nas, jak wycenić opcję kupna dającą
wypłatę końcową ![]() , gdy
, gdy ![]() .
.
a) Skorzystamy z metod matematyki ubezpieczeniowej. Dla ustalonego
scenariusza wartość dzisiejsza strumienia pieniędzy jest równa sumie
zdyskontowanych przepływów.
Zatem możemy przypuszczać, że cena opcji jest wartością obecną
opcji, a tę liczymy jako wartość oczekiwaną zdyskontowanej wypłaty.
Wobec tego cena opcji ![]() jest równa
jest równa
ponieważ ![]() i
i ![]() .
.
Tak wyliczona cena opcji jest równa ![]() , ale nikt rozsądny nie
będzie kupował opcji za tę cenę, gdyż lepiej kupić za te pieniądze
, ale nikt rozsądny nie
będzie kupował opcji za tę cenę, gdyż lepiej kupić za te pieniądze
![]() akcji. Wynika to z faktu, że gdy cena akcji wzrośnie, to
akcji. Wynika to z faktu, że gdy cena akcji wzrośnie, to ![]() akcji jest warte
akcji jest warte ![]() , a opcja daje wypłatę 5, a gdy cena akcji
wynosi
, a opcja daje wypłatę 5, a gdy cena akcji
wynosi ![]() , to opcja jest bezwartościowa.
Inwestycja w akcje daje zawsze większy zysk niż opcja. Przy tej
wycenie na rynku pojawiła się możliwość uzyskania zysku bez ryzyka.
Sprzedajemy opcje i za uzyskane pieniądze kupujemy akcje. Nie
zainwestowaliśmy żadnych własnych pieniędzy, a w chwili 1 mamy pewny
zysk.
, to opcja jest bezwartościowa.
Inwestycja w akcje daje zawsze większy zysk niż opcja. Przy tej
wycenie na rynku pojawiła się możliwość uzyskania zysku bez ryzyka.
Sprzedajemy opcje i za uzyskane pieniądze kupujemy akcje. Nie
zainwestowaliśmy żadnych własnych pieniędzy, a w chwili 1 mamy pewny
zysk.
b) Poprzednia sytuacja wynikła z przyjęcia założenia, że oba
scenariusze wydarzeń są równoprawdopodobne. Załóżmy, że scenariusze
mają różne szanse realizacji. Niech scenariusz niekorzystny ma 3
razy większe szanse zajścia. Wtedy ![]() ,
, ![]() i
i
Jeśli inny inwestor będzie miał inne wyobrażenie o rzeczywistości
i przyjmie na przykład, że ![]() , to wtedy
, to wtedy
![]() .
.
Tu oczywiście widać, że tak wyznaczona wielkość zależy od wyboru
prawdopodobieństwa ![]() , zatem od oszacowania rynku przez inwestora.
Gdy dla innego inwestora oszacowanie szans zmian na rynku
, zatem od oszacowania rynku przez inwestora.
Gdy dla innego inwestora oszacowanie szans zmian na rynku ![]() jest
inne, to i wartość zdyskontowana wypłaty będzie inna. Która wielkość
uznać za cenę? Czym jest cena?
jest
inne, to i wartość zdyskontowana wypłaty będzie inna. Która wielkość
uznać za cenę? Czym jest cena?
Zajmiemy się teraz znalezieniem właściwego sposobu wyceny opcji.
Chcemy wycenić je w zgodzie z cenami aktywa bazowego danymi
przez rynek, a więc szukamy ceny opcji w terminach cen rynkowych
aktywa bazowego.
Jak już zauważyliśmy, opcję europejską można utożsamiać z wypłatą.
Od tej pory każde aktywo pochodne będziemy utożsamiali z wypłatą ![]() generowaną przez to aktywo.
Wypłata zależy od scenariusza, więc
generowaną przez to aktywo.
Wypłata zależy od scenariusza, więc ![]() jest zmienną losową.
jest zmienną losową.
Definicja 2.1
Dowolną zmienną losową określoną na ![]() nazwiemy
wypłatą
nazwiemy
wypłatą ![]() w chwili
w chwili ![]() .
.
W tym modelu jest oczywiste, że dowolna
wypłata ![]() dla pewnego
dla pewnego ![]() . Okazuje się, że można dobrze
wycenić wypłatę korzystając z idei portfela replikującego.
Portfelem nazwiemy parę liczb
. Okazuje się, że można dobrze
wycenić wypłatę korzystając z idei portfela replikującego.
Portfelem nazwiemy parę liczb ![]() , gdzie
, gdzie
![]() jest liczbą posiadanych akcji w chwili zero, zaś
jest liczbą posiadanych akcji w chwili zero, zaś
![]() jest wysokością wkładu bankowego (ewentualnie wielkością
kredytu, gdy
jest wysokością wkładu bankowego (ewentualnie wielkością
kredytu, gdy ![]() w chwili zero. Dla przykładu, portfel
w chwili zero. Dla przykładu, portfel
![]() oznacza, że w portfelu są cztery akcje, czyli inwestor
kupił 4 akcje i pożyczył 2 z banku (2 jednostki pieniądza). Każda
para
oznacza, że w portfelu są cztery akcje, czyli inwestor
kupił 4 akcje i pożyczył 2 z banku (2 jednostki pieniądza). Każda
para ![]() tworzy portfel, co
odzwierciedla fakt, że można handlować dowolną liczbą aktywów (są
one doskonale podzielne), dopuszczenie wartości ujemnych
tworzy portfel, co
odzwierciedla fakt, że można handlować dowolną liczbą aktywów (są
one doskonale podzielne), dopuszczenie wartości ujemnych ![]() oznacza, że możemy dowolnie dużo pożyczać, a dopuszczenie wartości
ujemnych
oznacza, że możemy dowolnie dużo pożyczać, a dopuszczenie wartości
ujemnych ![]() oznacza, że rynek ten dopuszcza także krótką
sprzedaż (short-selling) akcji. Krótka sprzedaż polega na
pożyczeniu i sprzedaży akcji w chwili 0 oraz odkupieniu tej samej
liczby akcji i ich zwrocie w chwili
oznacza, że rynek ten dopuszcza także krótką
sprzedaż (short-selling) akcji. Krótka sprzedaż polega na
pożyczeniu i sprzedaży akcji w chwili 0 oraz odkupieniu tej samej
liczby akcji i ich zwrocie w chwili ![]() . Posługując się żargonem
finansowym, mówimy, że inwestor zajął pozycję krótką w akcjach.
Zbiór wszystkich możliwych portfeli oznaczać będziemy przez
. Posługując się żargonem
finansowym, mówimy, że inwestor zajął pozycję krótką w akcjach.
Zbiór wszystkich możliwych portfeli oznaczać będziemy przez ![]() .
W modelu, który przyjęliśmy
.
W modelu, który przyjęliśmy ![]() . Przy innych
założeniach o rynku zbiór wszystkich rozważanych portfeli może mieć
inną postać, np. gdy nie dopuszczamy krótkiej sprzedaży,
a dopuszczamy możliwość wzięcia kredytu to
. Przy innych
założeniach o rynku zbiór wszystkich rozważanych portfeli może mieć
inną postać, np. gdy nie dopuszczamy krótkiej sprzedaży,
a dopuszczamy możliwość wzięcia kredytu to ![]() .
.
Niech ![]() będzie portfelem inwestora.
Wartość (bogactwo) portfela
będzie portfelem inwestora.
Wartość (bogactwo) portfela ![]() w chwili
w chwili
![]() , oznaczane przez
, oznaczane przez ![]() , wynosi dla
, wynosi dla ![]() i
i ![]() odpowiednio:
odpowiednio:
Tak jest, gdyż skład portfela ustaliliśmy w chwili początkowej
(![]() ) i nie ulega on zmianie do chwili końcowej równej
) i nie ulega on zmianie do chwili końcowej równej ![]() .
.
Inwestor sprzedający wypłatę ![]() musi umieć ją zabezpieczyć, co
oznacza, że wartość portfela, który sprzedający wypłatę zbudował za
otrzymane ze sprzedaży pieniądze musi być w chwili
musi umieć ją zabezpieczyć, co
oznacza, że wartość portfela, który sprzedający wypłatę zbudował za
otrzymane ze sprzedaży pieniądze musi być w chwili ![]() równa
równa ![]() .
.
Definicja 2.2
Mówimy, że portfel ![]() replikuje wypłatę
replikuje wypłatę ![]() , gdy wartość
końcowa portfela jest równa
, gdy wartość
końcowa portfela jest równa ![]() , czyli
, czyli
dla ![]() .
.
Portfel replikujący jest doskonałym
zabezpieczeniem wypłaty ![]() , gdyż eliminuje całkowicie ryzyko
związane z niepewnością, który scenariusz się zrealizuje. Na
pytanie, dla jakich wypłat istnieje portfel replikujący odpowiada
, gdyż eliminuje całkowicie ryzyko
związane z niepewnością, który scenariusz się zrealizuje. Na
pytanie, dla jakich wypłat istnieje portfel replikujący odpowiada
Twierdzenie 2.1
Dla każdej wypłaty istnieje dokładnie
jeden portfel replikujący. Dla wypłaty ![]() ma on postać
ma on postać
| (2.4) |
gdzie ![]() ,
, ![]() .
.
Portfel replikujący ![]() dla
wypłaty
dla
wypłaty ![]() jest zadany przez układ równości:
jest zadany przez układ równości:
| (2.5) | |||||
| (2.6) |
i ma dokładnie jedno rozwiązanie dane wzorem (2.4) dla
dowolnych ![]() ,
, ![]() , zatem dla dowolnej wypłaty portfel jest
wyznaczony jednoznacznie.
, zatem dla dowolnej wypłaty portfel jest
wyznaczony jednoznacznie.
Naturalnym jest zdefiniowanie
ceny racjonalnej (godziwej) wypłaty ![]() jako początkowej
inwestycji potrzebnej do konstrukcji portfela replikującego, czyli:
jako początkowej
inwestycji potrzebnej do konstrukcji portfela replikującego, czyli:
Definicja 2.3
Racjonalną ceną w chwili ![]() wypłaty
wypłaty ![]() nazywamy liczbę
nazywamy liczbę
| (2.7) |
gdzie ![]() jest portfelem replikującym wypłatę
jest portfelem replikującym wypłatę ![]() .
.
Z tej definicji wynika, że racjonalna cena wypłaty nie zależy od
subiektywnych ocen prawdopodobieństw zmian cen akcji, nie zależy
więc od prawdopodobieństwa ![]() . Ta cecha ceny racjonalnej pozwala
uznać ją za obiektywny miernik wartości wypłaty w przyjętym modelu.
Należy podkreślić, że w tym modelu wszyscy inwestorzy zgadzają się
co do przyszłych wielkości cen akcji, czyli do tego że ceny mogą
przyjmować dwie znane z góry wartości.
. Ta cecha ceny racjonalnej pozwala
uznać ją za obiektywny miernik wartości wypłaty w przyjętym modelu.
Należy podkreślić, że w tym modelu wszyscy inwestorzy zgadzają się
co do przyszłych wielkości cen akcji, czyli do tego że ceny mogą
przyjmować dwie znane z góry wartości.
Ćwiczenie 2.1
Znaleźć cenę
racjonalną wypłaty ![]() .
.
Korzystając z tw. 2.1 otrzymujemy, że cena
racjonalna wypłaty ![]() jest równa
jest równa
| (2.8) |
Ćwiczenie 2.2
Niech ![]() .
Inwestor uważa, że prawdopodobieństwo wzrostu ceny akcji wynosi
.
Inwestor uważa, że prawdopodobieństwo wzrostu ceny akcji wynosi
![]() , a spadku
, a spadku ![]() .
Akcja kosztująca teraz
.
Akcja kosztująca teraz ![]() za 3 miesiące będzie miała cenę
za 3 miesiące będzie miała cenę
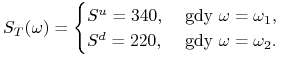 |
Niech stopa procentowa na depozyt 3-miesięczny wynosi
![]() . Wycenić opcję kupna z ceną wykonania
. Wycenić opcję kupna z ceną wykonania ![]() i momentem
wygaśnięcia za 3 miesiące.
i momentem
wygaśnięcia za 3 miesiące.
Wypłata z tej opcji ma postać
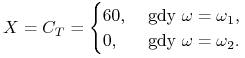 |
Portfel ![]() replikuje opcję, gdy
replikuje opcję, gdy ![]() , czyli gdy
, czyli gdy
dla ![]() i dla
i dla ![]() . Zatem dla
wartości podanych w przykładzie otrzymujemy, że portfel
. Zatem dla
wartości podanych w przykładzie otrzymujemy, że portfel ![]() jest portfelem replikującym, gdy
jest portfelem replikującym, gdy
Ten układ równań ma dokładnie jedno rozwiązanie:
Stąd cena racjonalna wypłaty ![]() z opcji jest równa
z opcji jest równa
Ćwiczenie 2.3
Opisać postępowanie inwestora sprzedającego opcję kupna i chcącego zabezpieczyć wypłatę z opcji. Co się dzieje, gdy opcja jest sprzedawana po cenie innej niż racjonalna?
W chwili ![]() inwestor postępuje następująco:
inwestor postępuje następująco:
| Działanie | rozliczenie |
|---|---|
| Sprzedaje jedną opcję | |
| Kupuje |
|
| Tworzy depozyt bankowy (ew. bierze kredyt) |
Na mocy definicji racjonalnej ceny mamy
Zatem koszt początkowy takiego postępowania inwestora sprzedającego opcję jest równy zeru.
W chwili ![]() inwestor postępuje następująco:
inwestor postępuje następująco:
| Działanie | rozliczenie |
|---|---|
| Realizuje opcję | |
| Sprzedaje akcje | |
| Podejmuje pieniądze z banku (ew. zwraca dług) |
Rozliczenie końcowe
czyli do tej transakcji nikt nie dołożył. Cena racjonalna wypłaty jest do zaakceptowania dla obu stron.
Gdyby opcja nie była sprzedawana po cenie ![]() , a po cenie
, a po cenie ![]() , to:
, to:
-
W przypadku, gdy
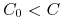 , sprzedający ma pewny zysk
, sprzedający ma pewny zysk 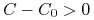 w chwili 0, gdyż wystarczy wydać
w chwili 0, gdyż wystarczy wydać 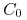 by zabezpieczyć wypłatę
by zabezpieczyć wypłatę 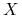 dla
kupującego, resztę sprzedający zachowuje dla siebie.
dla
kupującego, resztę sprzedający zachowuje dla siebie. -
Gdy
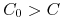 (koszt zabezpieczenia jest większy niż cena
(koszt zabezpieczenia jest większy niż cena 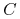 ), to
kupujący ma pewny zysk
), to
kupujący ma pewny zysk 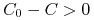 w chwili 0, gdyż aby otrzymać
wypłatę
w chwili 0, gdyż aby otrzymać
wypłatę 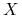 musiałby wydać
musiałby wydać 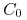 , a kupił ją za
, a kupił ją za 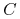 .
.
W obu przypadkach, gdy ![]() (tj. cena różni się od ceny
racjonalnej), znajdujemy portfel dający zysk bez żadnego ryzyka
i zajmując odpowiednią pozycję mamy dodatni dochód.
(tj. cena różni się od ceny
racjonalnej), znajdujemy portfel dający zysk bez żadnego ryzyka
i zajmując odpowiednią pozycję mamy dodatni dochód.
W ten sposób opisaliśmy rynek podając ceny ![]() instrumentu
ryzykownego, wartość
instrumentu
ryzykownego, wartość ![]() jednostki rachunku bankowego i zbiór
możliwych portfeli
jednostki rachunku bankowego i zbiór
możliwych portfeli ![]() . Rynek
. Rynek ![]() jest zatem trójką
jest zatem trójką
Na tym rynku potrafimy wycenić każdą wypłatę (czyli każdy instrument
pochodny). Jednak powyższy model rynku trzeba jeszcze poprawić, gdyż
dopuszcza on sytuację, że dla dodatniej wypłaty ![]() może się
okazać, że jej cena jest ujemna, czyli
może się
okazać, że jej cena jest ujemna, czyli ![]() .
.
Ćwiczenie 2.4
Znaleźć przykład rynku i wypłaty ![]() , której cena racjonalna jest
ujemna, tj.
, której cena racjonalna jest
ujemna, tj. ![]() .
.
Korzystamy z postaci ceny, czyli z (2.8). Ponieważ
![]() , więc gdy
, więc gdy ![]() , to musi być
, to musi być
![]() lub
lub ![]() . Teraz łatwo dobrać liczby
spełniające warunki zadania, np.
. Teraz łatwo dobrać liczby
spełniające warunki zadania, np. ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() . Wtedy
. Wtedy ![]() . Na
tym rynku możemy osiągnąć zysk bez ryzyka pożyczając 10 jednostek
z banku i kupując za tę kwotę akcję. Wtedy w chwili
. Na
tym rynku możemy osiągnąć zysk bez ryzyka pożyczając 10 jednostek
z banku i kupując za tę kwotę akcję. Wtedy w chwili ![]() sprzedając
akcję otrzymujemy co najmniej 12, a do banku musimy zwrócić 11.
sprzedając
akcję otrzymujemy co najmniej 12, a do banku musimy zwrócić 11.
W tej sytuacji można by osiągnąć zysk bez ryzyka za pomocą odpowiedniej strategii. Stąd
Definicja 2.4
Mówimy, że w modelu ![]() nie ma możliwości arbitrażu
nie ma możliwości arbitrażu ![]() model
nie dopuszcza możliwości arbitrażu
model
nie dopuszcza możliwości arbitrażu ![]() , gdy nie istnieje portfel
, gdy nie istnieje portfel
![]() , taki że
, taki że
Portfel ![]() , dla którego powyższe warunki są spełnione
nazywamy możliwością arbitrażu.
, dla którego powyższe warunki są spełnione
nazywamy możliwością arbitrażu.
Zatem model ![]() rynku jest wolny od arbitrażu, gdy nie ma
możliwości arbitrażu w klasie portfeli (strategii)
rynku jest wolny od arbitrażu, gdy nie ma
możliwości arbitrażu w klasie portfeli (strategii) ![]() .
Interpretacja portfela arbitrażowego jest klarowna: nie mając nic na
początku, stosując strategię
.
Interpretacja portfela arbitrażowego jest klarowna: nie mając nic na
początku, stosując strategię ![]() , na końcu operacji nic nie
stracimy i mamy dodatni zysk dla pewnych scenariuszy.
, na końcu operacji nic nie
stracimy i mamy dodatni zysk dla pewnych scenariuszy.
Istnienie możliwości arbitrażu świadczy o serii poważnych błędów w wycenie instrumentów na rynku. Takie błędy są bardzo szybko wychwytywane przez arbitrażystów, skutkiem czego rynek szybko wraca do równowagi. Zatem model rynku powinien być modelem bez możliwości arbitrażu. Zbadamy wobec tego, jakie warunki trzeba narzucić na model rynku, by nie dopuszczał on możliwości arbitrażu.
Twierdzenie 2.2
Rynek jest wolny od arbitrażu wtedy i tylko wtedy, gdy
| (2.9) |
Ze wzoru (2.3) widać, że warunek (2.9) jest równoważny warunkowi
| (2.10) |
![]() Chcemy pokazać, że nie istnieje arbitraż. Weźmy portfel
Chcemy pokazać, że nie istnieje arbitraż. Weźmy portfel
![]() , taki że
, taki że ![]() , czyli
, czyli ![]() . Gdy
. Gdy ![]() , to
, to ![]() , zatem
, zatem ![]() ,
, ![]() i ten portfel nie jest portfelem
arbitrażowym. Gdy
i ten portfel nie jest portfelem
arbitrażowym. Gdy ![]() , to ten portfel w chwili T ma
wartość:
, to ten portfel w chwili T ma
wartość:
![V_{{T}}(\varphi)=\alpha S_{{T}}+\beta(1+r)=\alpha S_{{T}}-\alpha S_{0}(1+r)=\begin{cases}\alpha s[u-(1+r)]&\text{ dla }\ Z=u,\\
\alpha s[d-(1+r)]&\text{ dla }\ Z=d.\end{cases}](wyklady/ip1/mi/mi289.png) |
Korzystając z (2.10) otrzymujemy, że portfel ![]() z zerowym kapitałem początkowym i
z zerowym kapitałem początkowym i ![]() w chwili końcowej
w chwili końcowej
![]() przyjmuje wartości różnych znaków, a mianowicie gdy
przyjmuje wartości różnych znaków, a mianowicie gdy ![]() , to
, to ![]() i
i ![]() ,
a gdy
,
a gdy ![]() to zachodzą nierówności przeciwne. Zatem portfel
to zachodzą nierówności przeciwne. Zatem portfel
![]() o zerowej wartości początkowej nie może być
arbitrażem.
o zerowej wartości początkowej nie może być
arbitrażem.
Ćwiczenie 2.5
Udowodnij implikację ![]() .
.
Nie wprost, niech jedna z powyższych nierówności nie zachodzi.
Załóżmy, że ![]() . Weźmy portfel
. Weźmy portfel ![]() , czyli
sprzedajemy krótko akcję i inwestujemy uzyskane z tej sprzedaży
pieniądze w rachunek bankowy. Wtedy proces bogactwa dla tej
strategii
, czyli
sprzedajemy krótko akcję i inwestujemy uzyskane z tej sprzedaży
pieniądze w rachunek bankowy. Wtedy proces bogactwa dla tej
strategii ![]() spełnia
spełnia ![]() następujące warunki:
następujące warunki:
oraz
Zatem ![]() jest arbitrażem. Sprzeczność.
jest arbitrażem. Sprzeczność.
Gdy ![]() , to przeprowadzamy analogiczne rozumowanie.
, to przeprowadzamy analogiczne rozumowanie.
Ćwiczenie 2.6
Udowodnić, że na rynku bez możliwości
arbitrażu cena racjonalna wypłaty nieujemnej jest nieujemna, czyli
![]() , gdy
, gdy ![]() . Gdy ponadto
. Gdy ponadto ![]() , to
, to
![]() .
.
Wykluczenie równości w (2.9) ma sens
ekonomiczny, gdyż wtedy wykluczamy sytuację, w której na rynku są
dwa aktywa, ale jednym z nich nikt nie handluje. Istotnie, gdy
![]() , to zawsze należy inwestować w akcje, bo
w najgorszym przypadku dadzą tyle, co depozyt w banku, a gdy
, to zawsze należy inwestować w akcje, bo
w najgorszym przypadku dadzą tyle, co depozyt w banku, a gdy
![]() , to zawsze należy wkładać pieniądze do banku, bo
depozyt da większy zysk niż akcje i to bez żadnego ryzyka. W obu
tych przypadkach rynek nie jest płynny i znika z niego jeden
z rodzajów aktywów.
, to zawsze należy wkładać pieniądze do banku, bo
depozyt da większy zysk niż akcje i to bez żadnego ryzyka. W obu
tych przypadkach rynek nie jest płynny i znika z niego jeden
z rodzajów aktywów.
Na rynku bez możliwości arbitrażu cena wypłaty (instrumentu
pochodnego ![]() ) jest dobrze określona. Wynika to z twierdzenia,
którego dowód przebiega w analogiczny sposób, jak rozumowanie w
ćwiczeniu 2.3.
) jest dobrze określona. Wynika to z twierdzenia,
którego dowód przebiega w analogiczny sposób, jak rozumowanie w
ćwiczeniu 2.3.
Twierdzenie 2.3
Cena w chwili ![]() wypłaty
wypłaty ![]() inna niż
inna niż ![]() , gdzie
, gdzie
![]() jest portfelem replikującym wypłatę
jest portfelem replikującym wypłatę ![]() , prowadzi do
arbitrażu.
, prowadzi do
arbitrażu.
Stąd ma sens
Definicja 2.5
Niech ![]() będzie rynkiem bez możliwości arbitrażu. Wtedy
cenę racjonalną instrumentu pochodnego
będzie rynkiem bez możliwości arbitrażu. Wtedy
cenę racjonalną instrumentu pochodnego ![]() nazywamy ceną arbitrażową
nazywamy ceną arbitrażową
![]() w chwili
w chwili ![]() na rynku
na rynku ![]() i oznaczamy
i oznaczamy
![]() .
.
Okazuje się, że rynek bez możliwości arbitrażu rozszerzony o instrument pochodny (np. o opcję) pozostaje dalej rynkiem, na którym nie istnieje arbitraż (patrz zad. 2.7).
2.3. Wycena za pomocą miary martyngałowej.
Przedstawimy teraz sposób wyliczania ceny instrumentów pochodnych na rynku bez możliwości arbitrażu, oparty na obliczaniu wartości oczekiwanej względem pewnej wyróżnionej miary probabilistycznej.
Przykład 2.2
Podobnie jak w rozważanym ćwiczeniu 2.2 przyjmijmy, że
![]() ,
, ![]() ,
, ![]() ,
, ![]() i niech
i niech ![]() . Wtedy
. Wtedy
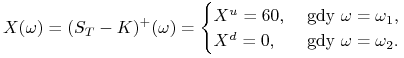 |
Łatwo obliczyć, że portfel replikujący ma
postać: ![]() i
i ![]() , a stąd
, a stąd ![]() . Zatem
. Zatem
![]() , a więc istnieje jedno
, a więc istnieje jedno ![]() takie, że
takie, że
czyli ![]() , gdzie
, gdzie ![]() ,
,
![]() . Okazuje się, że dla tego rozkładu
prawdopodobieństwa
. Okazuje się, że dla tego rozkładu
prawdopodobieństwa ![]() zachodzi także
zachodzi także
Czy to jest przypadek wynikający ze szczególnego doboru danych? Czy cena jest wartością oczekiwaną wypłaty względem pewnego rozkładu?
W tym przykładzie ![]() nie zależy od prawdopodobieństwa subiektywnego
nie zależy od prawdopodobieństwa subiektywnego
![]() , potencjalnie zależy zaś od wypłaty
, potencjalnie zależy zaś od wypłaty ![]() , a jednocześnie
dla cen akcji zachodzi
, a jednocześnie
dla cen akcji zachodzi ![]() . Chciałoby się, aby
w sytuacji ogólnej
. Chciałoby się, aby
w sytuacji ogólnej ![]() (a więc rozkład
(a więc rozkład ![]() ) zależało tylko od cen
) zależało tylko od cen
![]() , a nie zależało od postaci funkcji
, a nie zależało od postaci funkcji ![]() . Okazuje się, że taki
rozkład można zawsze znaleźć. Pokazanie tego będzie naszym
celem.
. Okazuje się, że taki
rozkład można zawsze znaleźć. Pokazanie tego będzie naszym
celem.
Rynek bez możliwości arbitrażu spełnia warunek (2.10)
z którego wynika, że ![]() , więc
, więc ![]() jest kombinacją
wypukłą końców odcinka, czyli istnieje
jest kombinacją
wypukłą końców odcinka, czyli istnieje ![]() , takie że
, takie że
| (2.11) |
Liczby ![]() i
i ![]() zadają nowe prawdopodobieństwo
zadają nowe prawdopodobieństwo ![]() ,
takie że
,
takie że
Wtedy korzystając z (2.11) otrzymujemy
Zatem zachodzi
| (2.12) |
czyli otrzymaliśmy wzór przedstawiający cenę dzisiejszą jako
zdyskontowaną wartość oczekiwaną ceny jutrzejszej względem
prawdopodobieństwa ![]() . Zwykle ważne są nie wielkości cen,
a proporcje pomiędzy nimi. Interesuje nas stosunek cen różnych
aktywów. W tym celu wyrażamy wszystko w terminach wartości jakiegoś
ustalonego aktywa. Najczęściej cenę jednostki w banku
. Zwykle ważne są nie wielkości cen,
a proporcje pomiędzy nimi. Interesuje nas stosunek cen różnych
aktywów. W tym celu wyrażamy wszystko w terminach wartości jakiegoś
ustalonego aktywa. Najczęściej cenę jednostki w banku ![]() (inwestycja bez ryzyka) uznajemy za jednostkę ceny na rynku
i wszystkie inne ceny wyrażamy w tych jednostkach (czyli dyskontem
jest rachunek bankowy). Wtedy jednostka na rachunku bankowym ma
stałą wartość: jeśli
(inwestycja bez ryzyka) uznajemy za jednostkę ceny na rynku
i wszystkie inne ceny wyrażamy w tych jednostkach (czyli dyskontem
jest rachunek bankowy). Wtedy jednostka na rachunku bankowym ma
stałą wartość: jeśli ![]() jest zdyskontowanym procesem wartości
jednostki w banku, tj.
jest zdyskontowanym procesem wartości
jednostki w banku, tj. ![]() , to
, to
Zamiast procesu cen rozważamy zdyskontowany proces cen
![]() :
:
Jest to konwencja techniczna, bardzo ułatwiająca obliczenia. Jak
było widać we wzorze (2.12), dla prawdopodobieństwa ![]() zachodzi równość:
zachodzi równość:
Dla rynku
jednookresowego dwustanowego jest to równoważne faktowi, że ![]() jest
jest ![]() -martyngałem z czasem
-martyngałem z czasem ![]() względem filtracji
względem filtracji ![]() ,
, ![]() , gdyż
, gdyż
![]() . Stąd definicja:
. Stąd definicja:
Definicja 2.6
Miarę probabilistyczną ![]() nazywamy miarą
martyngałową dla zdyskontowanego procesu cen
nazywamy miarą
martyngałową dla zdyskontowanego procesu cen ![]() , gdy miara
, gdy miara ![]() jest równoważna z
jest równoważna z ![]() oraz
oraz ![]() jest
jest ![]() -martyngałem.
-martyngałem.
Przypomnijmy, że miara ![]() jest równoważna z
jest równoważna z ![]() , gdy obie mają te
same zbiory miary zero. Z założenia
, gdy obie mają te
same zbiory miary zero. Z założenia ![]() , dla
, dla ![]() , więc miara
, więc miara ![]() równoważna z
równoważna z ![]() spełnia ten sam
warunek:
spełnia ten sam
warunek: ![]() , dla
, dla ![]() .
.
Lemat 2.1
Na rynku ![]() istnieje miara martyngałowa
istnieje miara martyngałowa
![]() dla zdyskontowanego procesu cen
dla zdyskontowanego procesu cen ![]() wtedy i tylko wtedy, gdy
jedyne rozwiązanie równania
wtedy i tylko wtedy, gdy
jedyne rozwiązanie równania
| (2.13) |
względem ![]() należy do przedziału
należy do przedziału ![]() .
.
![]() Gdy
Gdy ![]() jest miarą martyngałową, to zachodzi
jest miarą martyngałową, to zachodzi ![]() , a stąd wynika (2.13)
i
, a stąd wynika (2.13)
i ![]() .
.
![]() Gdy (2.13) ma rozwiązanie
Gdy (2.13) ma rozwiązanie ![]() , to definiując miarę probabilistyczną
, to definiując miarę probabilistyczną ![]() wzorem
wzorem
![]() otrzymujemy
miarę
otrzymujemy
miarę ![]() równoważną z
równoważną z ![]() i spełniającą
i spełniającą ![]() .
Stąd
.
Stąd ![]() jest miarą martyngałową.
jest miarą martyngałową.
Uwaga 2.1
Jedyne rozwiązanie równania (2.13) jest postaci
| (2.14) |
więc miara martyngałowa ![]() jest zadana
przez wielkości wyznaczające cenę i przez wielkość stopy
procentowej.
jest zadana
przez wielkości wyznaczające cenę i przez wielkość stopy
procentowej.
Obecnie możemy sformułować podstawowe twierdzenie tego paragrafu:
Twierdzenie 2.4
Rynek ![]() jest wolny od
arbitrażu wtedy i tylko wtedy, gdy istnieje miara martyngałowa dla
zdyskontowanego procesu cen
jest wolny od
arbitrażu wtedy i tylko wtedy, gdy istnieje miara martyngałowa dla
zdyskontowanego procesu cen ![]() . Wtedy cena arbitrażowa w chwili
. Wtedy cena arbitrażowa w chwili
![]() dowolnej wypłaty
dowolnej wypłaty ![]() w chwili
w chwili ![]() jest dana wzorem
jest dana wzorem
| (2.15) |
gdzie ![]() jest miarą martyngałową.
jest miarą martyngałową.
Pierwsza część twierdzenia wynika z lematu 2.1, tw. 2.2, uwagi 2.1 oraz z tego, że
Został do udowodnienia wzór (2.15) podający cenę arbitrażową.
Niech ![]() będzie jedynym portfelem
replikującym
będzie jedynym portfelem
replikującym ![]() . Wówczas:
. Wówczas:
przy czym trzecia od końca równość wynika z faktu, iż ![]() jest
miarą martyngałową, zaś ostatnia z definicji
jest
miarą martyngałową, zaś ostatnia z definicji ![]() .
.
Uwaga (ważna) 2.2
a) Cenę arbitrażową pochodnych obliczamy w świecie neutralnym wobec ryzyka, ale nie oznacza to, że żyjemy (lub uważamy, że żyjemy) w takim świecie.
b) Cena arbitrażowa wyliczona według wzoru (2.15) nie zależy
od preferencji, czyli wyboru prawdopodobieństwa ![]() dla modelu
ewolucji cen instrumentu bazowego (stąd niektórzy nazywają ją miarą
niezależną od preferencji. Zależy tylko od nośnika miary
dla modelu
ewolucji cen instrumentu bazowego (stąd niektórzy nazywają ją miarą
niezależną od preferencji. Zależy tylko od nośnika miary ![]() —
jest taka sama dla wszystkich miar równoważnych. Oznacza to, że
inwestorzy zgadzają się co do wielkości przyszłych cen instrumentu
bazowego, choć różnią się oceną prawdopodobieństwa wystąpienia
konkretnych cen. Zatem rolą
—
jest taka sama dla wszystkich miar równoważnych. Oznacza to, że
inwestorzy zgadzają się co do wielkości przyszłych cen instrumentu
bazowego, choć różnią się oceną prawdopodobieństwa wystąpienia
konkretnych cen. Zatem rolą ![]() jest określenie, jakie zdarzenia są
możliwe, a jakie nie są możliwe.
jest określenie, jakie zdarzenia są
możliwe, a jakie nie są możliwe. ![]() wyznacza nam klasę miar
równoważnych.
wyznacza nam klasę miar
równoważnych.
c) Jako czynnik dyskontujący wybraliśmy proces ![]() , ale to nie jest
istotne, można jako czynnik dyskontujący wybrać proces cen
, ale to nie jest
istotne, można jako czynnik dyskontujący wybrać proces cen ![]() (patrz ćw. 2.12).
(patrz ćw. 2.12).
d) Wzór (2.15) uzasadnia nazywanie miary martyngałowej ![]() miarą wyceniającą.
Z
(2.15) wynika, że dzisiejsza cena arbitrażowa (tzn. dla
miarą wyceniającą.
Z
(2.15) wynika, że dzisiejsza cena arbitrażowa (tzn. dla
![]() ) wypłaty
) wypłaty ![]() jest równa wartości średniej, przy mierze
wyceniającej, zdyskontowanej wypłaty (a więc wypłaty liczonej przy
dzisiejszej wartości pieniądza).
jest równa wartości średniej, przy mierze
wyceniającej, zdyskontowanej wypłaty (a więc wypłaty liczonej przy
dzisiejszej wartości pieniądza).
Parytet (formuła zgodności) dla cen opcji. Okazuje się, że
ceny europejskich opcji kupna i sprzedaży z tą samą ceną wykonania
![]() na rynku bez możliwości arbitrażu są związane wzorem, tzw.
parytetem kupna-sprzedaży:
na rynku bez możliwości arbitrażu są związane wzorem, tzw.
parytetem kupna-sprzedaży:
| (2.16) |
Wzór (2.16) wynika z podzielenia obu stron równości
(1.4) przez ![]() i zastosowania wzoru
(2.15) na cenę. Parytet (wzór (2.16)) pozwala
natychmiast podać cenę opcji sprzedaży, gdy znamy cenę opcji kupna
i vice versa.
i zastosowania wzoru
(2.15) na cenę. Parytet (wzór (2.16)) pozwala
natychmiast podać cenę opcji sprzedaży, gdy znamy cenę opcji kupna
i vice versa.
Monotoniczność ceny. Na rynku rzeczywistym większa wypłata kosztuje więcej i sensowny model rynku musi to uwzględniać.
Twierdzenie 2.5
Monotoniczność ceny
Gdy rynek jest wolny od arbitrażu oraz wypłaty ![]() i
i ![]() spełniają
spełniają ![]() , to
, to
Twierdzenie wynika natychmiast ze wzoru (2.15) i własności wartości oczekiwanej
Stąd mamy intuicyjnie oczywisty
Wniosek 2.1
. Niech na rynku bez możliwości
arbitrażu ![]()
![]() odpowiednio
odpowiednio ![]() oznacza cenę opcji kupna
oznacza cenę opcji kupna
![]() odpowiednio sprzedaży
odpowiednio sprzedaży![]() z ceną wykonania
z ceną wykonania ![]() . Wtedy
. Wtedy
-
(i)
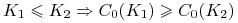 ,
, -
(ii)
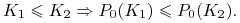
2.4. Kontrakt terminowy forward
Kontrakt terminowy forward jest umową zawartą w chwili początkowej
![]() , w której jedna ze stron zobowiązuje się kupić, druga zaś
sprzedać pewne dobro (zwykle papier wartościowy) w ustalonej chwili
, w której jedna ze stron zobowiązuje się kupić, druga zaś
sprzedać pewne dobro (zwykle papier wartościowy) w ustalonej chwili
![]() w przyszłości (tj.
w przyszłości (tj. ![]() ) za określoną z góry cenę. Kontrakty
forward są zawierane wyłącznie na rynku pozagiełdowym kontraktów
negocjowanych (over-the-counter market). Kontrakt taki może
opiewać na dowolny instrument z indywidualnie negocjowaną ceną, datą
i miejscem dostawy. Rzeczywiste dostarczenie towaru jest obiektem
transakcji — wieńczy ono ponad 90% kontraktów. Są jednak
kontrakty, które kończą się rozliczeniem pieniężnym, np. kontrakty
forward na stopy procentowe (wynika to z faktu, że bazą kontraktu
jest instrument nie będący przedmiotem bezpośredniego obrotu).
W chwili zawarcia kontraktu w chwili
) za określoną z góry cenę. Kontrakty
forward są zawierane wyłącznie na rynku pozagiełdowym kontraktów
negocjowanych (over-the-counter market). Kontrakt taki może
opiewać na dowolny instrument z indywidualnie negocjowaną ceną, datą
i miejscem dostawy. Rzeczywiste dostarczenie towaru jest obiektem
transakcji — wieńczy ono ponad 90% kontraktów. Są jednak
kontrakty, które kończą się rozliczeniem pieniężnym, np. kontrakty
forward na stopy procentowe (wynika to z faktu, że bazą kontraktu
jest instrument nie będący przedmiotem bezpośredniego obrotu).
W chwili zawarcia kontraktu w chwili ![]() nie następuje żaden
przepływ gotówki ani towaru — ma on miejsce dopiero w chwili
nie następuje żaden
przepływ gotówki ani towaru — ma on miejsce dopiero w chwili ![]() ,
w dniu realizacji kontraktu. Kontrakty forward są używane zarówno do
spekulacji jak i do zabezpieczenia się.
,
w dniu realizacji kontraktu. Kontrakty forward są używane zarówno do
spekulacji jak i do zabezpieczenia się.
Strona, która zobowiązuje się do zapłaty określonej w kontrakcie
kwoty za dobro, zajmuje pozycję długą w kontrakcie forward,
a strona, która zobowiązuje się dostarczyć to dobro, zajmuje pozycję
krótką. Z punktu widzenia pozycji długiej wypłata jest równa różnicy
pomiędzy wartością instrumentu bazowego (dobra) w chwili ![]() , a ceną
dostawy
, a ceną
dostawy ![]() uzgodnioną w kontrakcie, np. gdy kontrakt opiewa na
akcje o cenie
uzgodnioną w kontrakcie, np. gdy kontrakt opiewa na
akcje o cenie ![]() , to
, to
Definicja 2.7
Cenę dostawy ![]() taką, że wartość kontraktu w chwili
taką, że wartość kontraktu w chwili ![]() jest
równa zeru, nazywamy ceną forward i oznaczamy
jest
równa zeru, nazywamy ceną forward i oznaczamy ![]() .
.
Cenę tę opisuje:
Twierdzenie 2.6
Załóżmy, że ![]() jest rynkiem
jednookresowym dwustanowym bez możliwości arbitrażu. Wtedy cena
forward
jest rynkiem
jednookresowym dwustanowym bez możliwości arbitrażu. Wtedy cena
forward ![]() instrumentu bazowego o cenie
instrumentu bazowego o cenie ![]() z terminem
dostawy
z terminem
dostawy ![]() jest równa:
jest równa:
Gdy ![]() , to wartość kontraktu jest równa
, to wartość kontraktu jest równa
Cena forward to taka cena dostawy ![]() , że
, że ![]() , zatem
, zatem
2.5. Zagadnienia i zadania na ćwiczenia
Ćwiczenie 2.7
Niech na rynku ![]() bez
możliwości arbitrażu,
bez
możliwości arbitrażu, ![]() będzie procesem ceny
arbitrażowej
wypłaty
będzie procesem ceny
arbitrażowej
wypłaty ![]() , czyli
, czyli ![]() ,
, ![]() . Niech
. Niech ![]() oznacza klasę portfeli składających się z akcji, jednostek rachunku
bankowego i jednostek instrumentu pochodnego o cenie
oznacza klasę portfeli składających się z akcji, jednostek rachunku
bankowego i jednostek instrumentu pochodnego o cenie ![]() . Udowodnić,
że rynek
. Udowodnić,
że rynek ![]()
![]() czyli rynek
czyli rynek ![]() rozszerzony
o instrument pochodny
rozszerzony
o instrument pochodny![]() jest rynkiem bez możliwości arbitrażu.
jest rynkiem bez możliwości arbitrażu.
(nie wprost). Załóżmy, że na rozszerzonym rynku występuje
możliwość arbitrażu, czyli istnieją takie ![]() ,
, ![]() ,
,
![]() , że:
, że:
| (2.17) |
i dla każdego ![]()
| (2.18) |
oraz istnieje ![]() taka, że
taka, że
| (2.19) |
Ponieważ wypłata ![]() jest osiągalna i
jest osiągalna i ![]() , więc
, więc
Stąd i z (2.17) mamy
| (2.20) |
Ponadto z (2.18)
| (2.21) | |||||
Biorąc ![]() spełniające (2.19) mamy dla tej
spełniające (2.19) mamy dla tej ![]() nierówność ostrą w (2.21), więc portfel
nierówność ostrą w (2.21), więc portfel ![]() jest możliwością arbitrażu
dla rynku
jest możliwością arbitrażu
dla rynku ![]() (bo z (2.20)
(bo z (2.20)
![]() ), co przeczy założeniom.
), co przeczy założeniom.
Ćwiczenie 2.8
Załóżmy, że akcja kosztująca 200 będzie za trzy miesiące miała cenę 150 lub 300, a stopa procentowa na depozyt trzymiesięczny jest równa 10%. Znależć cenę europejskiej opcji sprzedaży z ceną wykonania 270 i terminem wykonania za trzy miesiące korzystając z obu poznanych metod.
Wypłata z tej opcji jest równa ![]() tzn.
tzn.
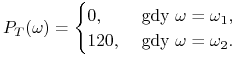 |
Zatem portfel replikujący spełnia równania:
(gdyż ![]() ), a stąd
), a stąd ![]() ,
,
![]() . Liczba akcji
. Liczba akcji ![]() jest liczbą ujemną, co
oznacza, że wystawca opcji sprzedaży zabezpieczając wypłatę dokonuje
krótkiej sprzedaży. Korzystając ze wzoru (2.8) otrzymujemy
cenę arbitrażową opcji:
jest liczbą ujemną, co
oznacza, że wystawca opcji sprzedaży zabezpieczając wypłatę dokonuje
krótkiej sprzedaży. Korzystając ze wzoru (2.8) otrzymujemy
cenę arbitrażową opcji:
Gdy zastosujemy metodę martyngałową, to obliczamy cenę ![]() korzystając ze wzorów (2.15) i (2.14):
korzystając ze wzorów (2.15) i (2.14):
Ćwiczenie 2.9
Udowodnić, że jeżeli istnieje portfel ![]() , taki
że
, taki
że ![]() oraz
oraz ![]() , to na rynku istnieje
arbitraż.
, to na rynku istnieje
arbitraż.
Gdy ![]() spełnia warunki zadania, to
portfel
spełnia warunki zadania, to
portfel ![]() jest arbitrażem, bo
jest arbitrażem, bo
![]() oraz
oraz ![]()
Ćwiczenie 2.10
[ Prawo jednej ceny] Udowodnić, że na rynku
jednookresowym dwustanowym bez możliwości arbitrażu portfele mające
tę samą wartość w chwili ![]() muszą mieć tę samą wartość w chwili 0.
muszą mieć tę samą wartość w chwili 0.
Niech ![]() będą takie, że
będą takie, że ![]() .
Wtedy, na mocy jedyności portfela replikującego na tym rynku,
.
Wtedy, na mocy jedyności portfela replikującego na tym rynku,
![]() , zatem
, zatem ![]() .
.
Ćwiczenie 2.11
Udowodnić parytet kupna-sprzedaży, czyli wzór (2.16), korzystając
a) z argumentów arbitrażowych,
b) z prawa jednej ceny (patrz zad. 1.2.10).
a) Nie wprost. Gdy
| (2.22) |
to strategia polegająca na kupnie akcji i opcji sprzedaży z ceną
wykonania ![]() i sprzedaniu opcji kupna z ceną wykonania
i sprzedaniu opcji kupna z ceną wykonania ![]() jest
strategią arbitrażową. Istotnie, wartość tej operacji, która jest
równa
jest
strategią arbitrażową. Istotnie, wartość tej operacji, która jest
równa ![]() rozliczamy w banku (gdy jest ona dodatnia, to
wkładamy tę sumę do banku, gdy ujemna, to pożyczamy ją z banku).
W chwili
rozliczamy w banku (gdy jest ona dodatnia, to
wkładamy tę sumę do banku, gdy ujemna, to pożyczamy ją z banku).
W chwili ![]() zawsze mamy zysk równy
zawsze mamy zysk równy
którego dodatniość wynika z warunku (2.22). Gdy
to zajęcie pozycji przeciwnej do opisanej wyżej jest strategią arbitrażową.
b) Portfel ![]() składający się z jednej akcji i pożyczki
w wysokości
składający się z jednej akcji i pożyczki
w wysokości ![]() i portfel
i portfel ![]() powstały w wyniku
zakupu opcji kupna i sprzedaży opcji sprzedaży o tej samej cenie
wykonania
powstały w wyniku
zakupu opcji kupna i sprzedaży opcji sprzedaży o tej samej cenie
wykonania ![]() mają w chwili
mają w chwili ![]() tę samą wartość
tę samą wartość ![]() , więc muszą
mieć tę samą wartość w chwili zero, co daje (2.16),
czyli parytet.
, więc muszą
mieć tę samą wartość w chwili zero, co daje (2.16),
czyli parytet.
Ćwiczenie 2.12
[ Różne dyskonta] Załóżmy, że proces cen ![]() jest
czynnikiem dyskontującym, czyli
jest
czynnikiem dyskontującym, czyli
Jest oczywiste, że miarę probabilistyczną ![]() taką, że
taką, że
![]() jest
jest ![]() –martyngałem nazywamy miarą martyngałową dla
procesu
–martyngałem nazywamy miarą martyngałową dla
procesu ![]() .
.
Udowodnić, że
a) na rynku nie ma możliwości arbitrażu wtedy i tylko wtedy, gdy
istnieje miara martyngałowa dla procesu ![]() .
.
b) na rynku bez możliwości arbitrażu cena wypłaty ![]() jest równa
jest równa
gdzie ![]() jest miarą martyngałową dla procesu
jest miarą martyngałową dla procesu ![]() .
.
Zatem jest to inny sposób wyceny wypłat.
a) ![]() jest miarą martyngałową dla
jest miarą martyngałową dla ![]() wtedy i tylko wtedy,
gdy
wtedy i tylko wtedy,
gdy
co z kolei jest równoważne z
Stąd otrzymujemy, że miara martyngałowa ![]() istnieje wtedy
i tylko wtedy, gdy rozwiązanie
istnieje wtedy
i tylko wtedy, gdy rozwiązanie ![]() równania
równania
czyli
należy do ![]() , co zachodzi wtedy i tylko wtedy, gdy
, co zachodzi wtedy i tylko wtedy, gdy ![]() (z postaci
(z postaci ![]() ) i stosujemy tw. 2.2.
) i stosujemy tw. 2.2.
Warto zauważyć, że ![]() zadaje miarę martyngałową
zadaje miarę martyngałową
![]() dla
dla ![]() i ta miara jest różna od miary martyngałowej
i ta miara jest różna od miary martyngałowej
![]() dla
dla ![]() .
.
b) Niech ![]() replikuje
replikuje ![]() (taki portfel
istnieje, na podstawie tw. 2.1). Wtedy
(taki portfel
istnieje, na podstawie tw. 2.1). Wtedy
![]() ,
, ![]() Stąd
Stąd
Ćwiczenie 2.13
Znaleźć na rynku jednookresowym dwustanowym wzory
ogólne na ceny europejskich opcji kupna i sprzedaży przy założeniu
![]() .
.
| (2.23) |
Ćwiczenie 2.14
Uzasadnić następujące ograniczenia na ceny opcji na rynku bez możliwości arbitrażu:
| (2.24) | |||||
| (2.25) |
Ćwiczenie 2.15
[ Zabezpieczenie doskonałe] Rozpatrzmy rynek bez
możliwości arbitrażu. Powiemy, że portfel ![]() jest doskonałym
zabezpieczeniem
wypłaty
jest doskonałym
zabezpieczeniem
wypłaty ![]() , gdy
, gdy ![]() . Ceną sprzedającego
. Ceną sprzedającego ![]() nazywamy minimalny koszt
zabezpieczenia doskonałego.
nazywamy minimalny koszt
zabezpieczenia doskonałego.
a) Udowodnić, że na rynku jednookresowym dwustanowym
![]()
b) Jak zdefiniować cenę kupującego ![]() ? Czy na rynku
jednookresowym dwustanowym zachodzi
? Czy na rynku
jednookresowym dwustanowym zachodzi ![]() ?
?
a) Cena sprzedającego jest zadana wzorem
Niech portfel ![]() replikuje wypłatę
replikuje wypłatę ![]() . Wtedy
. Wtedy ![]() , więc portfel
, więc portfel ![]() jest doskonałym zabezpieczeniem wypłaty
jest doskonałym zabezpieczeniem wypłaty
![]() , zatem
, zatem
Udowodnimy, że zachodzi nierówność przeciwna.
Gdy portfel ![]() jest taki, że
jest taki, że ![]() to
z monotoniczności ceny zachodzi
to
z monotoniczności ceny zachodzi ![]() , zatem
, zatem
![]() , a stąd
, a stąd
Inny sposób rozwiązania — to rozwiązanie zagadnienia minimalizacji z ograniczeniami, szukamy
przy ograniczeniach:
W wyniku tego postępowania też otrzymujemy ![]()
b) Zdefiniujemy cenę kupującego.
Z punktu widzenia kupującego warto zapłacić za wypłatę ![]() taką
wielkość
taką
wielkość ![]() , żeby w chwili
, żeby w chwili ![]() kupujący miał jeszcze co najmniej
taki sam zysk, jak w przypadku, gdy użyje strategii o cenie
początkowej
kupujący miał jeszcze co najmniej
taki sam zysk, jak w przypadku, gdy użyje strategii o cenie
początkowej ![]() . Stąd maksymalna cena akceptowana przez kupującego
to
. Stąd maksymalna cena akceptowana przez kupującego
to
Z własności supremum wynika, że ![]() . Zatem
korzystając z punktu a) otrzymujemy
. Zatem
korzystając z punktu a) otrzymujemy
Można też, analogicznie jak w przypadku ceny sprzedającego, szukać ceny kupującego jako rozwiązania zagadnienia maksymalizacji z odpowiednimi ograniczeniami.
Ćwiczenie 2.16
Gdy rozważamy rynek z kosztami za transakcje, to w naszym opisie rynku musimy wiele zmienić. Opisać różnicę pomiędzy kontraktami (gdy nie ma kosztów, to oba dają tę samą wypłatę):
a) sprzedający zobowiązuje się dostarczyć kupującemu akcję za cenę
![]() , gdy
, gdy ![]() ,
,
b) sprzedający wypłaca kupującemu różnicę ![]() , gdy
, gdy ![]() .
.
Ponieważ występują koszty, więc posiadanie w chwili ![]() kwoty
kwoty ![]() pieniędzy nie wystarcza do zakupu akcji (trzeba jeszcze pokryć
koszty tego zakupu). Wartość portfela nie może być utożsamiana
z liczbą, jest bowiem obiektem wielowymiarowym. Portfel jest opisany
przez dwie zmienne losowe, z których pierwsza mówi, ile pieniędzy
jest na rachunku bankowym, a druga — ile akcji jest w portfelu.
pieniędzy nie wystarcza do zakupu akcji (trzeba jeszcze pokryć
koszty tego zakupu). Wartość portfela nie może być utożsamiana
z liczbą, jest bowiem obiektem wielowymiarowym. Portfel jest opisany
przez dwie zmienne losowe, z których pierwsza mówi, ile pieniędzy
jest na rachunku bankowym, a druga — ile akcji jest w portfelu.




